Atención y el Transformador

Atención

Presentamos el concepto de “atención” antes de hablar sobre la arquitectura del Transformador. Existen dos tipos principales de atención: auto atención y atención cruzada. Dentro de esas categorías, distinguimos entre atención “suave” y atención “dura”.

Como veremos más adelante, los transformadores están constituidos por módulos de atención, los cuales son asociaciones entre conjuntos, y no entre secuencias, lo cual significa que no hace falta imponer un orden en nuestras entradas y salidas.

Auto Atención (I)

Consideremos un conjunto de $t$ entradas $\boldsymbol{x}$’s:

donde cada $\boldsymbol{x}_i$ es un vector $n$-dimensional. Puesto que el conjunto tiene $t$ elementos, y cada uno de ellos pertenece a $\mathbb{R}^n$, podemos representar el conjunto como una matriz $\boldsymbol{X}\in\mathbb{R}^{n \times t}$.

En el caso de la auto atención, la representación oculta $h$ es una combinación lineal de las entradas:

Usando la representación matricial descrita arriba, podemos escribir la capa oculta como el producto matricial:

donde $\boldsymbol{a} \in \mathbb{R}^t$ es un vector columna con componentes $\alpha_i$.

Nótese que esto difiere de la representación oculta que hemos visto hasta ahora, donde las entradas son multiplicadas por una matriz de pesos.

Dependiendo de las restricciones que impongamos en el vector $\vect{a}$, podemos conseguir atención dura o atención suave.

Atención Dura

En la atención dura, imponemos las siguientes restricciones en las alfas: $\Vert\vect{a}\Vert_0 = 1$. Esto significa que $\vect{a}$ es un vector con codificación “one-hot”. Por lo tanto, todos los coeficientes (con excepción de uno) son iguales a cero en la combinación lineal de las entradas, y la representación interna se reduce a la entrada $\boldsymbol{x}_i$ que corresponde al elemento $\alpha_i=1$.

Atención Suave

En la atención suave, imponemos que $\Vert\vect{a}\Vert_1 = 1$. La representación interna es una combinación lineal de las entradas donde la suma de los coeficientes es igual a 1.

Auto Atención (II)

¿De dónde vienen los términos $\alpha_i$?

Obtenemos el vector $\vect{a} \in \mathbb{R}^t$ de la siguiente manera:

Donde $\beta$ representa el parámetro de temperatura inversa de $\text{soft(arg)max}(\cdot)$. $\boldsymbol{X}^{\top}\in\mathbb{R}^{t \times n}$ es la representación en forma de transpuesta matricial del conjunto $\lbrace\boldsymbol{x}_i \rbrace_{i=1}^t$, y $\boldsymbol{x}$ representa un $\boldsymbol{x}_i$ genérico del conjunto. Nótese que la fila $j$-th de $X^{\top}$ corresponde a un elemento $\boldsymbol{x}_j\in\mathbb{R}^n$, de forma que la fila $j$-th de $\boldsymbol{X}^{\top}\boldsymbol{x}$ es el producto escalar de $\boldsymbol{x}_j$ con cada $\boldsymbol{x}_i$ en $\lbrace \boldsymbol{x}_i \rbrace_{i=1}^t$.

Los componentes del vector $\vect{a}$ son también llamados “puntajes” porque el producto escalar entre dos vectores nos dice que tan similares parecen ser. Por lo tanto, los elementos de $\vect{a}$ proveen información sobre la similitud del conjunto en su totatalidad con respecto a un $\boldsymbol{x}_i$ en particular.

Los corchetes representan un argumento opcional. Nótese que si se utiliza $\arg\max(\cdot)$, obtenemos un vector con codificación “one-hot” de alfas, lo cual resulta en atención dura. Por otro lado, $\text{soft(arg)max}(\cdot)$ resulta en atención suave. En ambos casos, la suma de los componentes del vector resultante $\vect{a}$ es igual a 1.

Al generar $\vect{a}$ de esta manera, se produce un conjunto de los mismos, uno por cada $\boldsymbol{x}_i$. Además, cada $\vect{a}_i \in \mathbb{R}^t$ de modo que podemos apilar las alfas en la matriz $\boldsymbol{A}\in \mathbb{R}^{t \times t}$.

Puesto que cada estado oculto es una combinación lineal de las entradas $\boldsymbol{X}$ y un vector $\vect{a}$, obtenemos un conjunto $t$ de estados ocultos, los cuales podemos apilar en una matriz $\boldsymbol{H}\in \mathbb{R}^{n \times t}$.

Almacén de clave/valor

Un almacén de clave/valor es un paradigma diseñado para almacenar (guardar), recuperar (consultar) y manejar arreglos asociativos (dicccionarios / tablas de hash.)

Por ejemplo, imaginemos que queremos encontrar una receta para hacer lasaña. Tenemos un libro de recetas y buscamos el término “lasaña” (esa sería la consulta). Esa consulta se verifica contra todas las posibles claves en el conjunto de datos (en este caso, éstas podrían ser todos los títulos de recetas en el libro). Verificamos que tan bien se alinea la consulta con cada título para encontrar la concordancia con mejor puntuación. Si nuestra salida es la función “argmax”, extraemos una única receta con el puntaje más alto. En caso contrario, si utilizamos la función “soft argmax”, obtendremos una distribución de probabilidades y podemos obtener una lista de recetas similares, desde la más parecida hasta la menos parecida.

En esencia, la consulta es la pregunta. Dada una consulta, la verificamos contra cada clave y obtenemos todo el contenido que concuerda.

Consultas, claves y valores

Cada uno de los vectores $\vect{q}, \vect{k}, \vect{v}$ puede ser visto como rotaciones de la entrada específica $\vect{x}$, donde $\vect{q}$ es simplemente $\vect{x}$ rotado por $\vect{W_q}$, $\vect{k}$ es $\vect{x}$ rotado por $\vect{W_k}$, y así de la misma forma para los demás $\vect{v}$. Nótese que ésta es la primera vez que presentamos parámetros “que se pueden aprender”, y no incluimos ninguna no-linearidad dado que la atención está basada completamente en orientación.

Con el fin de comparar la consulta contra todas las posibles claves, $\vect{q}$ and $\vect{k}$ deben tener la misma dimensionalidad; es decir, $\vect{q}, \vect{k} \in \mathbb{R}^{d’}$.

Sin embargo, $\vect{v}$ puede ser de cualquier dimensión. Si continuamos con nuestro ejemplo de la lasaña, necesitamos que la consulta tenga la misma dimensión que las claves (que son los títulos de las diferentes recetas en las que estamos buscando.) No obstante lo anterior, la dimensión de la receta que encontremos puede ser arbitrariamente larga, de modo que $\vect{v} \in \mathbb{R}^{d’’}$.

Por simplicidad, haremos la suposición de que todo tiene dimensión $d$; es decir:

Así que ahora tenemos un conjunto $\vect{x}$’s, un conjunto de consultas, un conjunto de claves y un conjunto de valores. Podemos agrupar estos conjuntos en matrices, cada una con $t$ columnas dado que agrupamos $t$ vectores, y cada vector columna con $d$ elementos.

Comparamos una consulta $\vect{q}$ contra la matriz de todas las claves $\vect{K}$:

Y ahora la capa oculta será la combinación lineal de las columnas de $\vect{V}$ ponderadas por los coeficientes en $\vect{a}$:

Dado que tenemos $t$ consultas, obtendremos sus $t$ pesos $\vect{a}$ correspondientes, y por ende una matriz $\vect{A}$ de dimensión $t \times t$.

Por lo tanto, en notación matricial tenemos:

Como un punto aparte, cabe mencionar que típicamente asignamos $\beta$ como:

Esto se hace para mantener la temperatura constante en las diversas elecciones de dimensión $d$, así que es necesario dividir por la raíz cuadrada del número de dimensiones $d$. (Imagínese cuál es la magnitud del vector $\vect{1} \in \R^d$.)

Para la implementación, podemos acelerar los cálculos agrupando todo los $\vect{W}$’s en un vector $\vect{W}$, y después calcular $\vect{q}, \vect{k}, \vect{v}$ de una sola vez:

Existe también el concepto de “cabezas”. Hemos visto previamente un ejemplo con una sola cabeza, pero es posible tener múltiples cabezas. Por ejemplo, digamos que tenemos $h$ cabezas. Entonces tenemos $h$ $\vect{q}$’s, $h$ $\vect{k}$’s y $h$ $\vect{v}$’s y terminamos con un vector en $\mathbb{R}^{3hd}$:

Sin embargo, aún es posible transformar los valores multi-cabeza para que tengan la dimensión original $\R^d$ usando un $\vect{W_h} \in \mathbb{R}^{d \times hd}$. Esta es sólo una de las posibles maneras de implementar el almacén de clave/valor.

El Transformador

Con el fin de expandir nuestro conocimiento sobre atención, interpretaremos ahora los bloques fundamentales del transformador. En particular, haremos un recorrido de principio a fin de un transformador básico, y veremos cómo se usa la atención en el paradigma estándar del codificador-decodificador, y cómo se compara esto con las arquitecturas secuenciales de las RNNs.

Arquitectura Codificador-Decodificador

Todos deberíamos estar familiarizados con esta terminología que se presenta de manera más prominente durante demostraciones del auto-codificador, y es un prerequisito conceptual en esta parte del curso. En resumen, el codificador-decodificador recibe una entrada e impone una clase de cuello de botella sobre la misma, forzando a que sólo la información más importante pase a través del mismo. Esta información se almacena en la salida del codificador, y puede ser utilizada para una variedad de tareas no relacionadas.

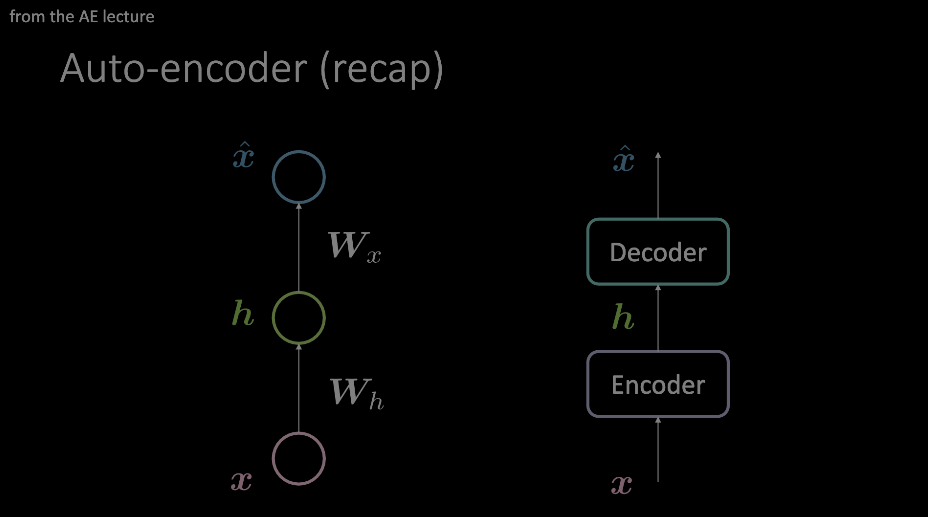
Figura 1: Dos diagramas ejemplificando un auto-codificador. El modelo de la izquierda muestra cómo un auto-codificador se puede diseñar con dos transformaciones afines + activaciones, mientras que el modelo de la derecha reemplaza esta "capa" única con un módulo arbitrario de operaciones.

Centremos ahora nuestra “atención” en la estructura del auto-codificador mostrado en el modelo de la derecha. Veremos a continuación cómo se ve por dentro en el contexto de transformadores.

Módulo de Codificación

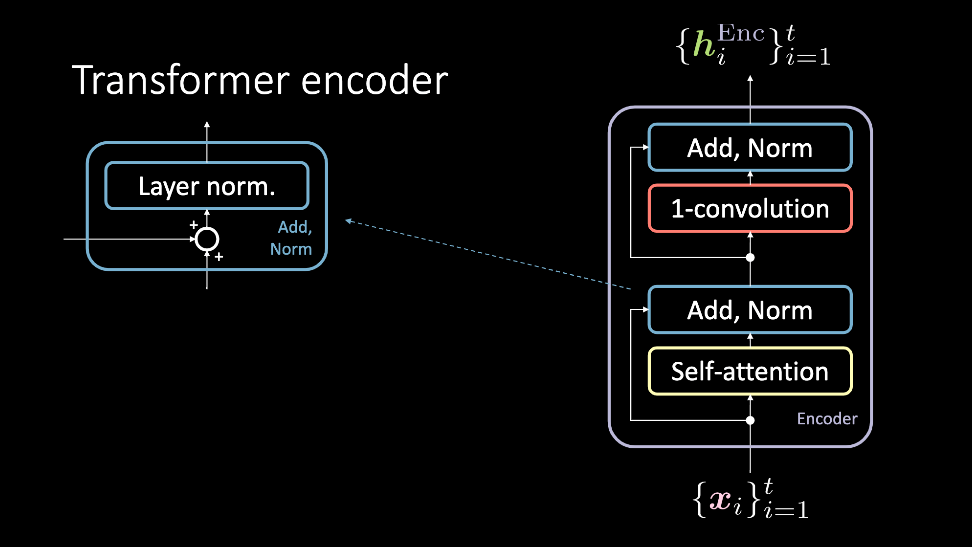
Figura 2: El codificador del transformador, que acepta un conjunto de entradas $\vect{x}$, y genera un conjunto de representaciones ocultas $\vect{h}^\text{Enc}$.

El módulo de codificación acepta un conjunto de entradas que alimentan de manera simultánea al bloque de atención y al bloque Add, Norm de manera directa. En este punto, la salida es nuevamente transmitida de manera simultánea a través de una convolución unidimensional y de otro bloque Add, Norm, para salir después en forma de representaciones ocultas. Este conjunto de representaciones ocultas se envía entonces a través de un número arbitrario de módulos de codificación (es decir, más capas similares), o hacia el decodificador. Revisaremos en más detalle ahora estos bloques.

Auto Atención

El modelo de auto atención es un modelo de atención normal. La consulta, clave y valor son generados a partir del mismo elemento de la entrada secuencial. En tareas que intentan modelar datos secuenciales, se agregan codificaciones posicionales previamente a este paso. La salida de este bloque son los valores ponderados por atención, y el bloque de auto atención acepta un conjunto de entradas $1, \cdots , t$ que generan como salida $1, \cdots, t$ valores ponderados por atención, los cuales son la entrada del resto del codificador.

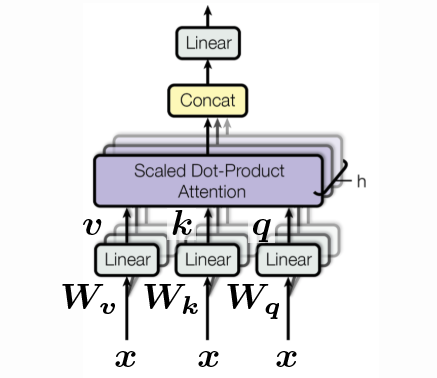
Figura 3: El bloque de auto atención. La secuencia de entradas se muestra como un conjunto a lo largo de la 3ra dimensión, y concatenado.

Add, Norm

El bloque Add, Norm tiene dos componentes. El primero es el bloque Add (que representa una conexión residual), seguido del bloque Norm, que es una capa de normalización.

Convolución Unidimensional

Después del paso anterior, se aplica una convolución unidimensional (también conocida como “red de avance por puntos” o “position-wise feed forward network” en inglés). Este bloque consta de dos capas densas. Dependiendo de que valores se establezcan, este bloque permite ajustar las dimensiones de la salida $\vect{h}^\text{Enc}$.

Módulo de Decodificación

El decodificador del transformador sigue un proceso similar al del codificador. Sin embargo, existe un sub-bloque adicional a considerar, además de que las entradas de este módulo son diferentes.

Figura 4: Una explicación más amena del decodificador.

Atención Cruzada

La atención cruzada utiliza la misma preparación para la consulta, la clave y el valor que se usa en los bloques de auto atención. Sin embargo, las entradas son un poco más complicadas. La entrada del decodificador es un dato $\vect{y}_i$ que se pasa a través de los bloques de auto atención y Add/Norm, y finalmente termina en los bloques de atención cruzada. Esto sirve como la consulta para la atención cruzada, donde los pares de clave/valor son la salida $\vect{h}^\text{Enc}$ que es calculada utilizando todas las salidas anteriores $\vect{x}_1, \cdots, \vect{x}_{t}$.

Resumen

Un conjunto $\vect{x}_1$ to $\vect{x}_{t}$ se alimenta a través del codificador. Utilizando auto atención y algunos otros bloques, se obtiene una representación de salida $\lbrace\vect{h}^\text{Enc}\rbrace_{i=1}^t$, la cual se alimenta al decodificador. Después de aplicarle auto atención, se le aplica atención cruzada. En este bloque, la consulta corresponde a una representación del símbolo en el lenguaje destino $\vect{y}_i$, y la clave y los valores provienen de la oración en el lenguaje origen ($\vect{x}_1$ to $\vect{x}_{t}$). De manera intuitiva podemos interpretar que la atención cruzada determina qué valores en la secuencia de entrada son lo más relevantes para construir $\vect{y}_t$, siendo, por tanto, merecedores de los coeficientes más altos de atención. La salida de esta atención cruzada se envía después a través de otro sub-bloque de convolución unidimensional, con lo cual obtenemos $\vect{h}^\text{Dec}$. A partir de aquí, es bastante claro ver cómo iniciar el entrenamiento para un lenguaje destino especificado, comparando $\lbrace\vect{h}^\text{Dec}\rbrace_{i=1}^t$ con datos pre-anotados.

Modelos de Lenguaje basados en Palabras

Hay algunos pocos hechos importantes que dejamos de lado al explicar los módulos más importantes del transformador, pero necesitamos discutirlos ahora para entender cómo los transformadores pueden lograr resultados de vanguardia en tareas de procesamiento de lenguaje.

Codificación Posicional

Los mecanismos de atención nos permiten ejecutar en paralelo las operaciones y acelerar enormemente el tiempo de entrenamiento, pero al hacerlo exista una pérdida de información secuencial. La posibilidad de agregar codificación posicional nos permite evitar perder este contexto.

Representaciones Semánticas

A lo largo del entrenamiento del transformador se generan muchas representaciones ocultas. Para crear un espacio de incrustación (“embedding space” en inglés) similar al que se utiliza en el ejemplo de modelo de lenguaje basado en palabras (implementado en PyTorch), la salida de la atención cruzada nos dará una representación semántica de la palabra $x_i$. A partir de ese punto, es posible realizar más experimentos sobre dichos datos de salida.

Resumen del Código

Veamos ahora los bloques de los transformadores que se trataron previamente, en un formato mucho más fácil de entender: ¡código!

El primer módulo que veremos es el bloque de atención multi-cabeza. Dependiendo de los valores de la consulta, la clave y los valores que se ingresen a este módulo, puede utilizarse tanto para auto atención como para atención cruzada.

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, p, d_input=None):
        super().__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        if d_input is None:
            d_xq = d_xk = d_xv = d_model
        else:
            d_xq, d_xk, d_xv = d_input
        # Embedding dimension of model is a multiple of number of heads
        # La dimensión de incrustación del modelo es un múltiplo del número de cabezas
        assert d_model % self.num_heads == 0
        self.d_k = d_model // self.num_heads
        # These are still of dimension d_model. To split into number of heads
        # Éstas aún son de dimensión `d_model`. Es necesario particionar en N número de cabezas
        self.W_q = nn.Linear(d_xq, d_model, bias=False)
        self.W_k = nn.Linear(d_xk, d_model, bias=False)
        self.W_v = nn.Linear(d_xv, d_model, bias=False)
        # Outputs of all sub-layers need to be of dimension d_model
        # Las salidas de todas las sub-capas necesitan ser de dimensión `d_model`
        self.W_h = nn.Linear(d_model, d_model)

Inicialización de la clase de atención multi-cabeza. Si se pasa un valor de d_input, se convierte en atención cruzada. De lo contrario, se convierte en auto atención. La preparación de la consulta, la clave y el valor se construye como una transformación lineal de la entrada d_model.

def scaled_dot_product_attention(self, Q, K, V):
    batch_size = Q.size(0)
    k_length = K.size(-2)

    # Scaling by d_k so that the soft(arg)max doesnt saturate
    # Escalamos por d_k para que soft(arg)max no se sature
    Q = Q / np.sqrt(self.d_k)  # (bs, n_heads, q_length, dim_per_head)
    scores = torch.matmul(Q, K.transpose(2,3))  # (bs, n_heads, q_length, k_length)

    A = nn_Softargmax(dim=-1)(scores)  # (bs, n_heads, q_length, k_length)

    # Get the weighted average of the values
    # Obtenemos el promedio ponderado de los valores
    H = torch.matmul(A, V)  # (bs, n_heads, q_length, dim_per_head)

    return H, A

Regresamos la capa oculta que corresponde a las codificaciones de valores después de ser escalados por el vector de atención. Para poder responder otras preguntas (p. ej. ¿qué valores en la secuencia fueron eliminados por la máscara de atención?), regresamos A también.

def split_heads(self, x, batch_size):
    return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

Dividimos la última dimensión en (heads × depth) y regresamos después de aplicar una transpuesta para ajustarlo a la forma (batch_size × num_heads × seq_length × d_k)

def group_heads(self, x, batch_size):
    return x.transpose(1, 2).contiguous().
        view(batch_size, -1, self.num_heads * self.d_k)

Combinamos las cabezas de atención para obtener la forma correcta que es consistente con el tamaño del lote y la longitud de la secuencia.

def forward(self, X_q, X_k, X_v):
    batch_size, seq_length, dim = X_q.size()
    # After transforming, split into num_heads
    # Después de transformar, divide en `num_heads`
    Q = self.split_heads(self.W_q(X_q), batch_size)
    K = self.split_heads(self.W_k(X_k), batch_size)
    V = self.split_heads(self.W_v(X_v), batch_size)
    # Calculate the attention weights for each of the heads
    # Calcula los pesos de atención para cada una de las cabezas
    H_cat, A = self.scaled_dot_product_attention(Q, K, V)
    # Put all the heads back together by concat
    # Reúne todas las cabezas concatenándolas
    H_cat = self.group_heads(H_cat, batch_size)  # (bs, q_length, dim)
    # Final linear layer
    # Capa lineal final
    H = self.W_h(H_cat)  # (bs, q_length, dim)
    return H, A

El recorrido hacia adelante de la atención multi-cabeza.

Dada una entrada, ésta se divide en q, k y v y dichos valores se alimentan a través de un mecanismo de atención basado en un producto punto escalado, después se concatenan y finalmente se hacen pasar por una última capa lineal. La última salida del bloque de atención es la atención encontrada, así como las representaciones ocultas que se pasan intactas a través de los bloques restantes.

No obstante, el siguiente bloque que se muestra en el transformador/codificador es el de Add, Norm, el cual viene incluido en PyTorch. Como tal, se trata de una implementación extremadamente simple y no requiere de una clase propia. Lo siguiente es el bloque de convolución unidimensional (revísense secciones previas para ver más detalles sobre el mismo.)

Ahora que tenemos todas nuestras clases principales, nos enfocaremos en el módulo del codificador.

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, conv_hidden_dim, p=0.1):
        self.mha = MultiHeadAttention(d_model, num_heads, p)
        self.layernorm1 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)
        self.layernorm2 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)

    def forward(self, x):
        attn_output, _ = self.mha(x, x, x)
        out1 = self.layernorm1(x + attn_output)
        cnn_output = self.cnn(out1)
        out2 = self.layernorm2(out1 + cnn_output)
        return out2

En los transformadores más poderosos, un número arbitrariamente grande de estos codificadores se apilan uno encima del otro.

Recordemos que la auto atención por sí misma no contiene ninguna recurrencia o convoluciones, pero es justamente eso lo que le da su gran eficiencia. Para hacerla susceptible a las posiciones de la entrada, podemos incluir codificaciones de posición, las cuales se calculan de la manera siguiente:

Con el fin de no entrar aquí en demasiados detalles finos, se puede revisar la liga https://github.com/Atcold/pytorch-Deep-Learning/blob/master/15-transformer.ipynb para ver el código fuente completo de lo descrito aquí.

Un codificador entero, con N capas de codificadores apiladas, así como codificaciones de posicionamiento, se escribe así:

class Encoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, ff_hidden_dim,
            input_vocab_size, maximum_position_encoding, p=0.1):
        self.embedding = Embeddings(d_model, input_vocab_size,
                                    maximum_position_encoding, p)
        self.enc_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.enc_layers.append(EncoderLayer(d_model, num_heads,
                                                ff_hidden_dim, p))
    def forward(self, x):
        x = self.embedding(x) # Transformar a (batch_size, input_seq_length, d_model)
        for i in range(self.num_layers):
            x = self.enc_layers[i](x)
        return x  # (batch_size, input_seq_len, d_model)

Ejemplo de Uso

Existen muchas tareas para las cuales se puede usar un codificador aislado. En el “notebook” que acompaña este documento, vemos cómo se puede utilizar un codificador para realizar análisis de sentimiento.

Utilizando el conjunto de datos de reseñas de IMDB, podemos generar como salida del codificador una representación latente de una secuencia de texto, y entrenar este proceso de codificación con entropía cruzada binaria como la función de pérdida, lo cual corresponde a una reseña positiva o negativa de una película.

Al igual que en el caso anterior, omitimos los detalles (los cuales se pueden revisar en el “notebook”), pero mostramos los componentes arquitectónicos más importantes del transformador:

class TransformerClassifier(nn.Module):
    def forward(self, x):
        x = Encoder()(x)
        x = nn.Linear(d_model, num_answers)(x)
        return torch.max(x, dim=1)

model = TransformerClassifier(num_layers=1, d_model=32, num_heads=2,
                         conv_hidden_dim=128, input_vocab_size=50002, num_answers=2)

Una vez armado de esta manera, dicho modelo se puede entrenar como cualquier otro.