Predicción y Aprendizaje de Políticas Bajo Incertidumbre (PPUU)

Introducción y planteamiento del problema

Digamos que queremos aprender a conducir de una manera que no involucre modelos de aprendizaje por refuerzo. En AR, entrenamos modelos dejando que el modelo cometa errores y aprenda de ellos, pero esta no es la mejor manera ya que estos errores pueden llevarnos al cielo o al infierno donde no tiene sentido el aprendizaje.

Entonces, hablemos de una manera más ‘humana’ de aprender a conducir un automóvil. Consideremos un ejemplo de cambio de carril. Suponiendo que el automóvil se mueve a 100 km/h, lo que se traduce aproximadamente en 30 m/s, si miramos 30 m frente a nosotros, estamos mirando aproximadamente 1 s hacia el futuro.

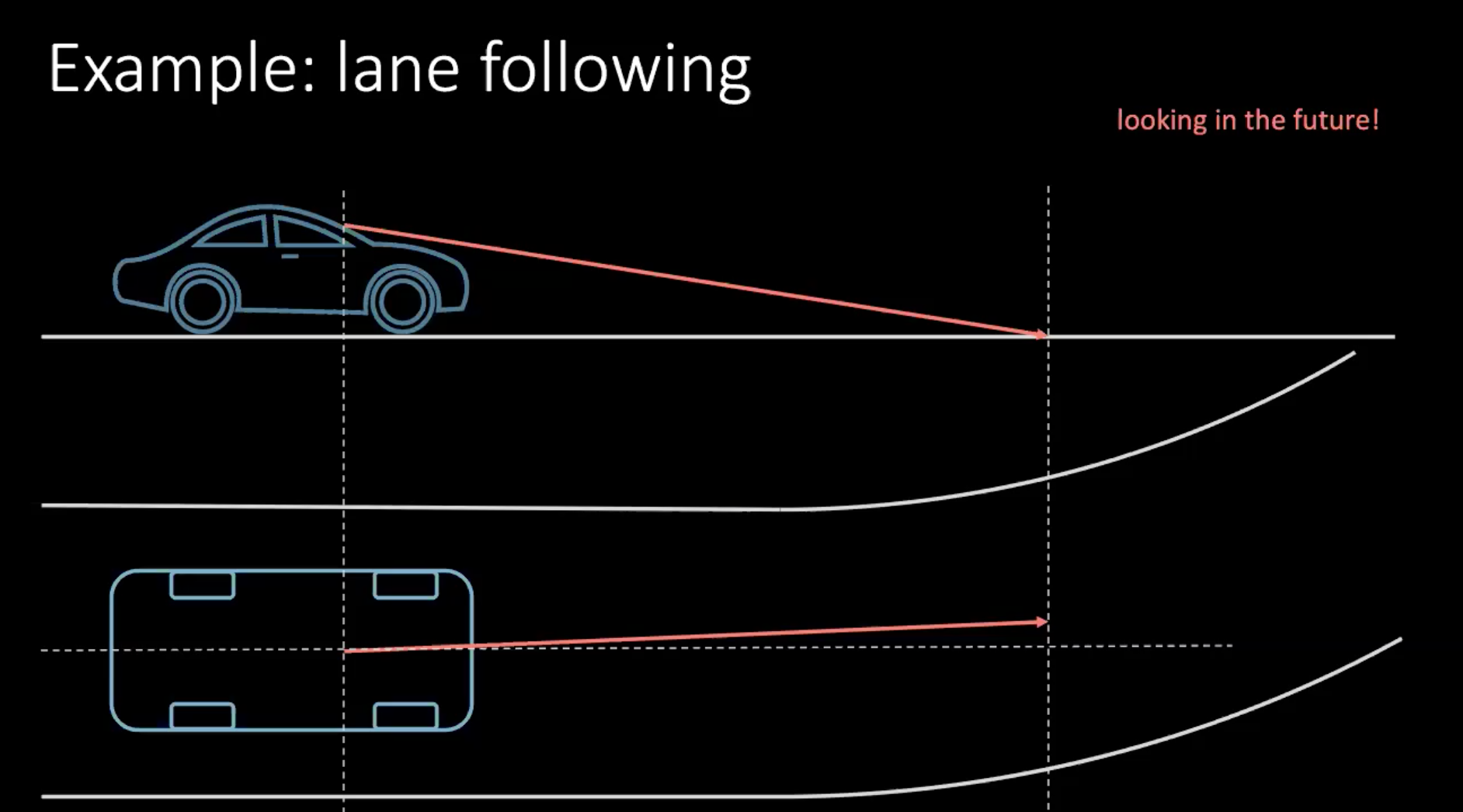
Figura 1: Mirando hacia el futuro mientras conducimos

Si estuviéramos girando, deberíamos tomar una decisión basada en el futuro cercano. Para poder girar en unos cuantos metros debemos realizar una acción ahora, que en este contexto es mover el volante. Tomar una decisión no solo depende de nuestra conducción, sino también de los vehículos circundantes en el tráfico. Dado que todos los que nos rodean no son tan deterministas, es muy difícil tener en cuenta todas las posibilidades.

Analicemos ahora lo que está sucediendo en este escenario. Tenemos un agente (representado aquí por un cerebro) que toma la entrada $s_t$​ (posición, velocidad e imágenes del contexto) y produce una acción $a_t$​(control de dirección, aceleración y frenado). El ambiente nos lleva a un nuevo estado y devuelve un costo $c_t$​.

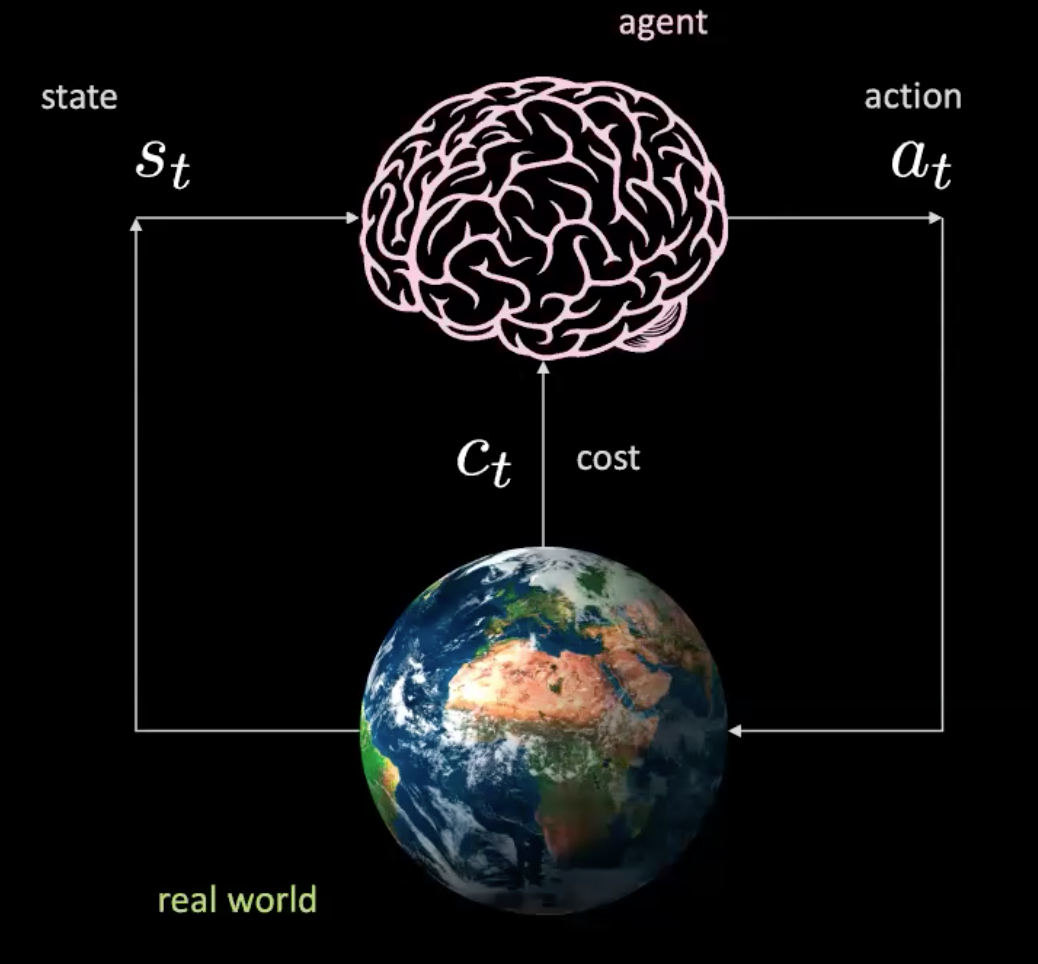
Figura 2: Ilustración de un agente en el mundo real

Esto es como una red sencilla en la que se toman acciones dado un estado específico y el mundo nos da el siguiente estado y la siguiente consecuencia. Esto no involucra modelos porque con cada acción estamos interactuando con el mundo real. Pero, ¿podemos entrenar a un agente sin interactuar realmente con el mundo real?

¡Si podemos! Averigüémoslo en la sección “Aprendiendo un modelo del mundo”.

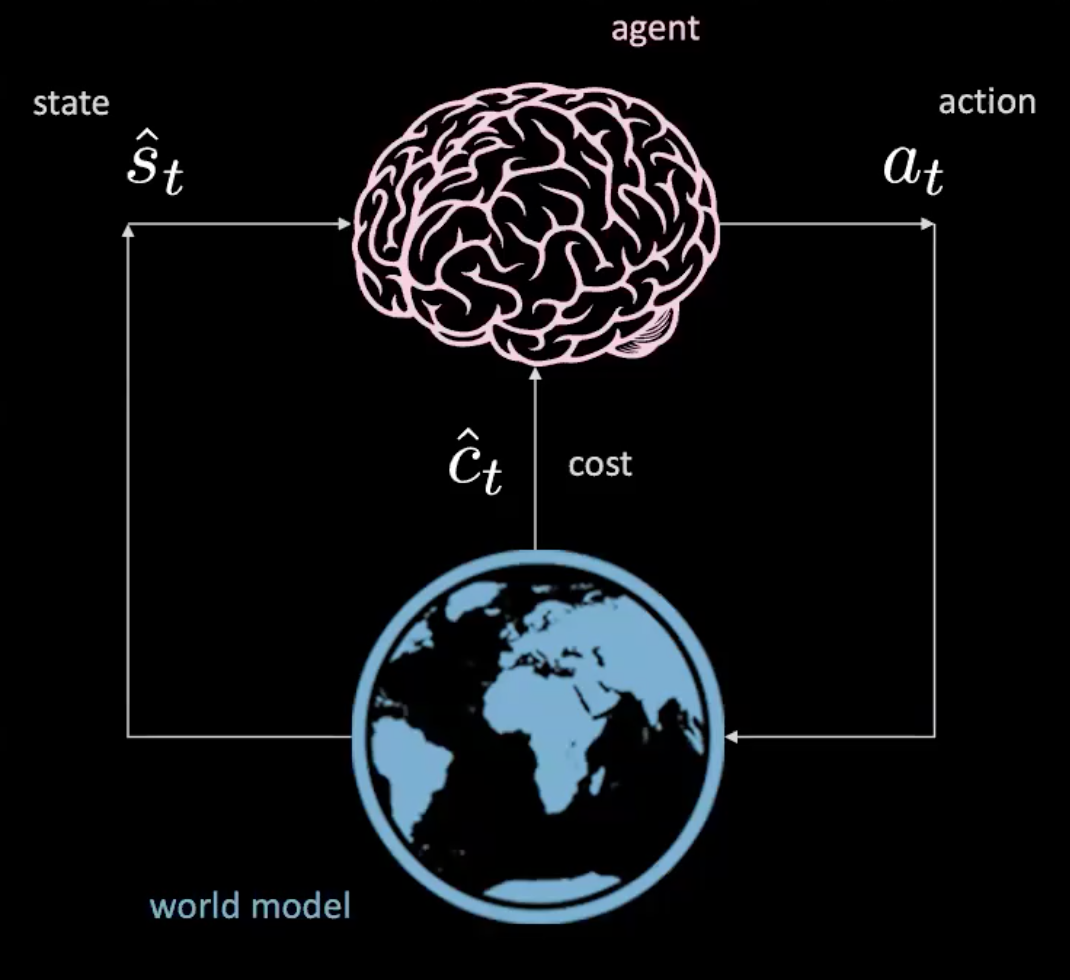
Figura 3: Ilustración de un agente en el modelo del mundo

Conjunto de datos

Antes de discutir cómo aprender el modelo del mundo, exploremos el conjunto de datos del que disponemos. Tenemos 7 cámaras montadas en la parte superior de un edificio de 30 pisos frente a la interestatal. Ajustamos las cámaras para obtener la vista desde arriba y luego extraemos los cuadros delimitadores para cada vehículo. Para un tiempo $t$, podemos determinar $p_t$ que representa la posición, $v_t$ la velocidad e $i_t$​ el estado actual del tráfico alrededor del vehículo.

Como conocemos la cinemática de la conducción, podemos invertirla para averiguar cuáles son las acciones que está realizando el conductor. Por ejemplo, si el automóvil realiza un movimiento rectilíneo uniforme, sabemos que la aceleración es cero (lo que significa que no hay acción)

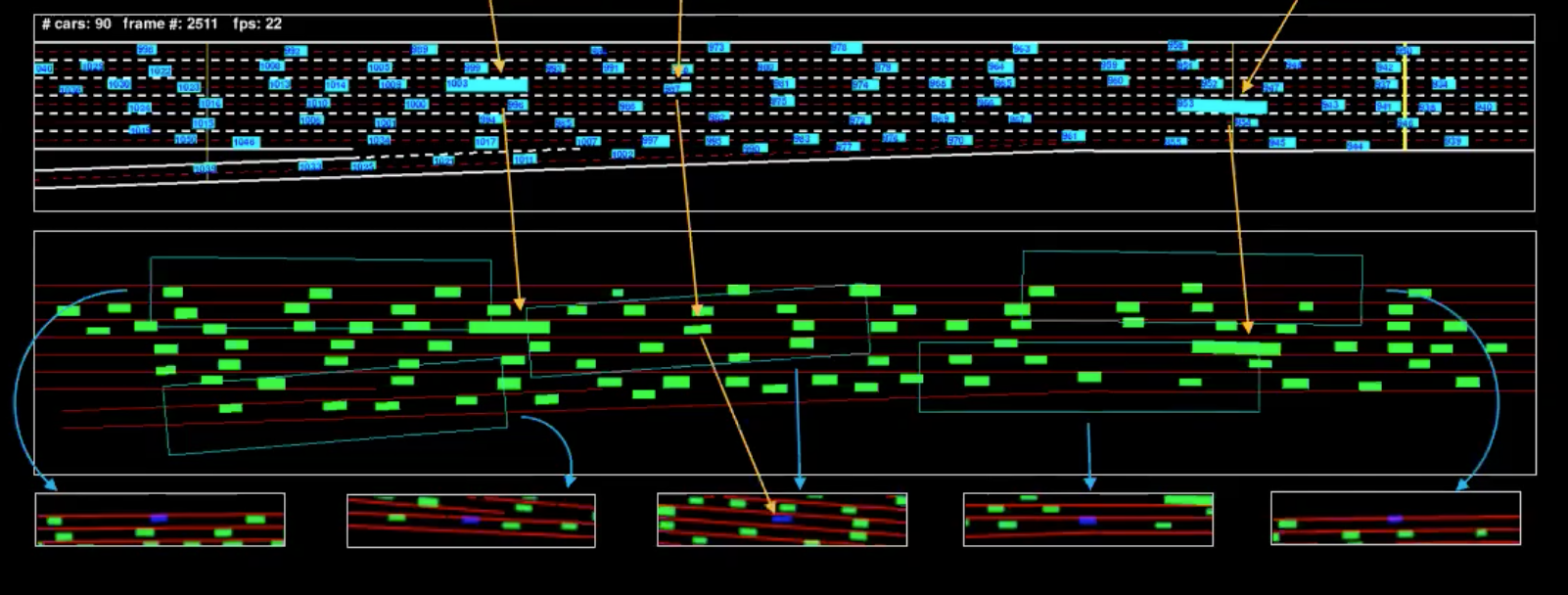
Figura 4: Representación del computador, para una sola toma

La ilustración en azul corresponde a los datos de entrada y la ilustración en verde es la representación del computador. Para entender esto mejor, hemos aislado algunos vehículos (marcados en la ilustración). Las representaciones que vemos abajo son los cuadros delimitadores correspondientes al campo de visión de estos vehículos.

Costo

Hay dos tipos diferentes de costos aquí: costo del carril y costo de proximidad. El costo del carril nos dice qué tan bien ubicados estamos dentro de un carril y el costo de proximidad nos dice qué tan cerca estamos de los otros autos.

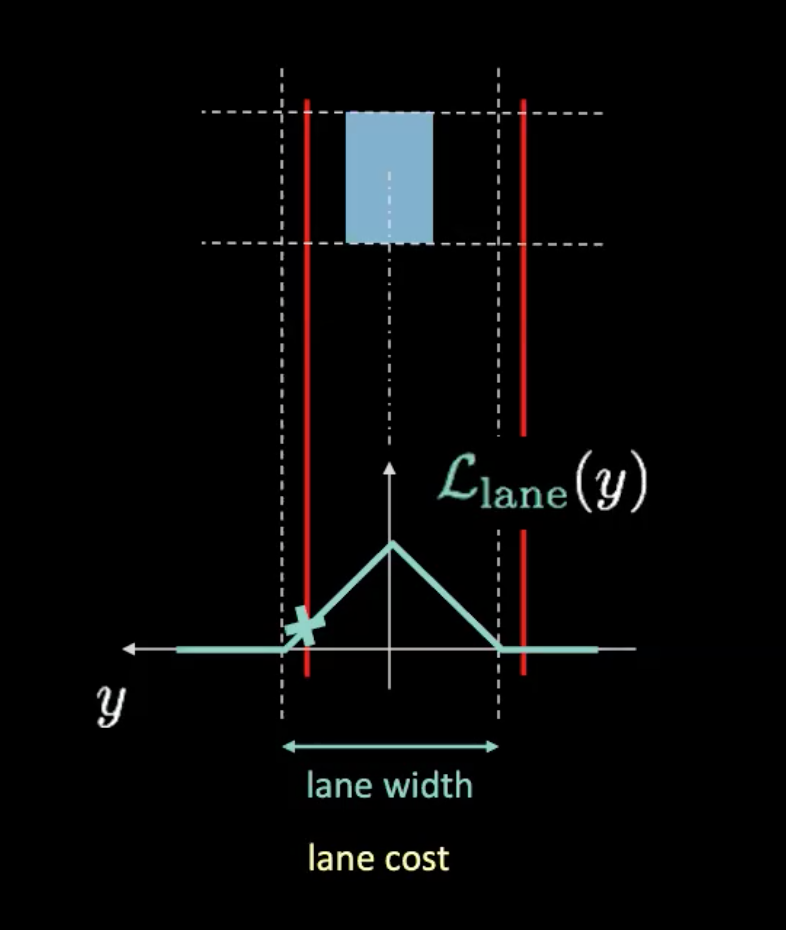
Figura 5: Costo del carril

En la figura anterior, las líneas punteadas representan carriles reales y las líneas rojas nos ayudan a calcular el costo del carril dada la posición actual de nuestro automóvil. Las líneas rojas se mueven a medida que nuestro automóvil se mueve. La altura de la intersección de las líneas rojas con la curva potencial (en cian) nos da el costo. Si el automóvil está en el centro del carril, ambas líneas rojas se superponen con los carriles reales, lo que resulta en un costo cero. Por otro lado, a medida que el automóvil se aleja del centro, las líneas rojas también se mueven para dar como resultado un costo distinto de cero.

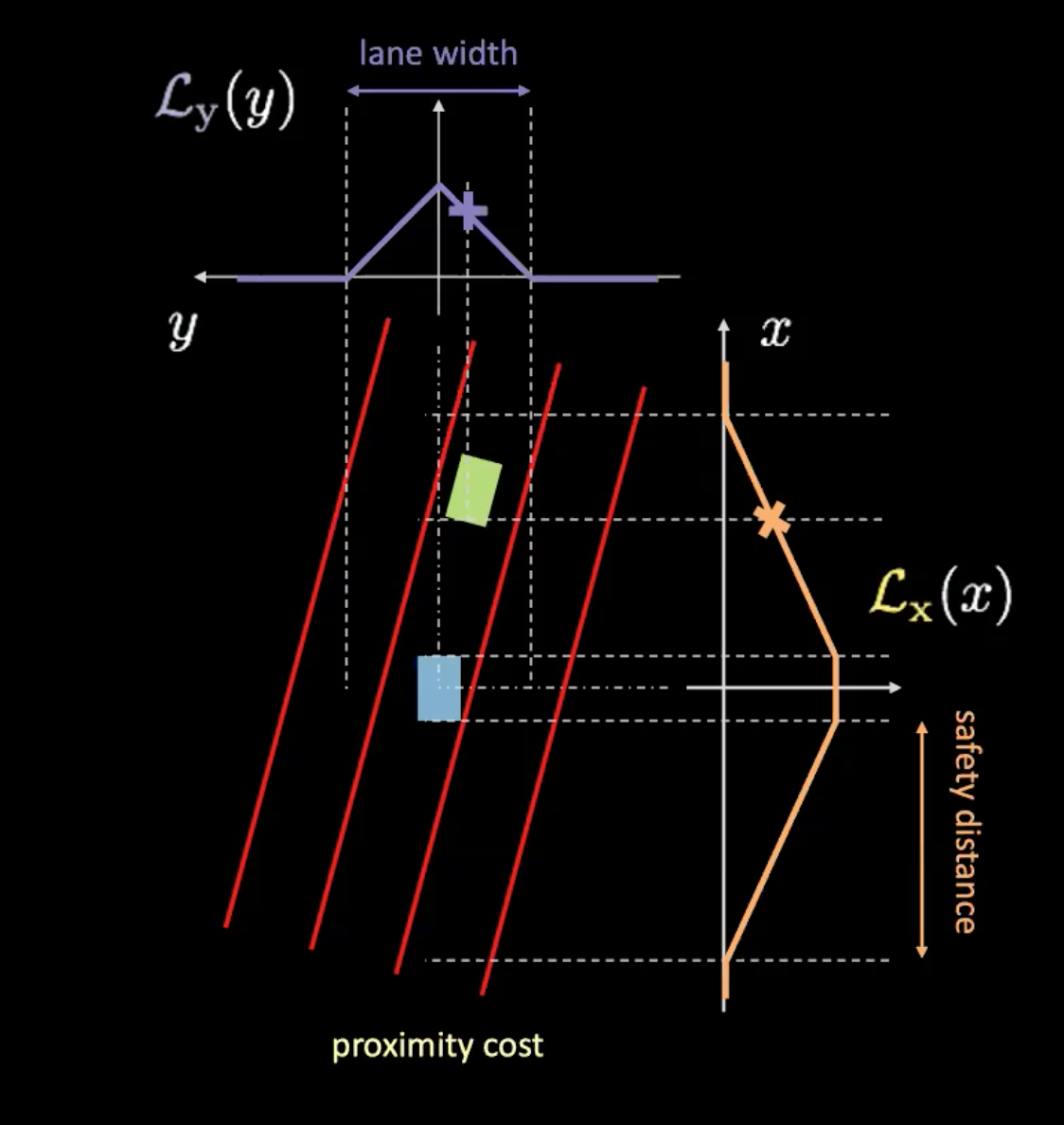
Figura 6: Costo de proximidad

El costo de proximidad tiene dos componentes ($\mathcal{L}_x$ y $\mathcal{L}_y$). $\mathcal{L}_y$ es similar al costo del carril y $\mathcal{L}_x$ ​depende de la velocidad de nuestro carro. La curva naranja de la Figura 6 nos informa sobre la distancia de seguridad. A medida que aumenta la velocidad del automóvil, la curva naranja se ensancha. Así que mientras más rápido viaja el automóvil, más se tendrá que mirar hacia adelante y hacia atrás. La altura de la intersección de un automóvil con la curva naranja determina $\mathcal{L}_x$.

El producto de estos dos componentes nos da el costo de proximidad.

Aprendiendo un modelo del mundo

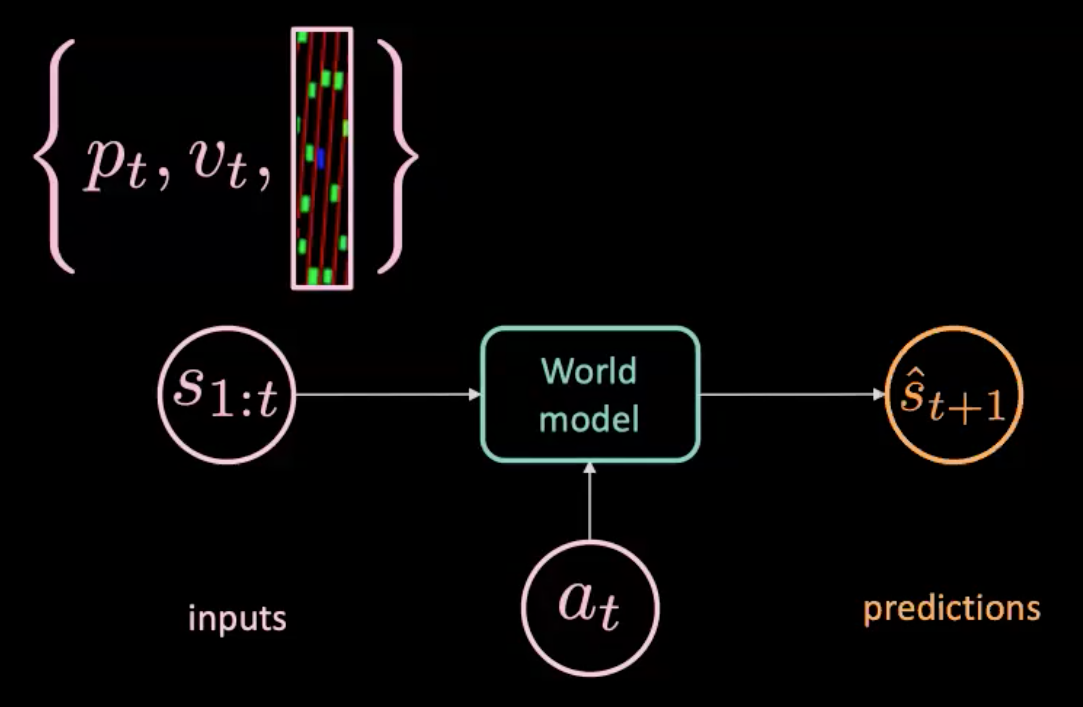
Figura 7: Ilustración del modelo del mundo

El modelo del mundo se alimenta de una acción $a_t$ (dirección, frenado y aceleración) y $s_{1:t}$​ (secuencia de estados donde cada estado está representado por posición, velocidad e imágenes de contexto en ese instante) y predice el siguiente estado $\hat s_{t+1}$​. Por otro lado, tenemos el mundo real que nos dice lo que realmente sucedió ($s_{t+1}$). Optimizamos MSE (error cuadrático medio) entre predicciones ($\hat s_{t+1}$) y objetivo ($s_{t+1}$) para entrenar nuestro modelo.

Predictor-decodificador determinista

Una forma de entrenar nuestro modelo del mundo es utilizando el modelo de predictor-decodificador que se explica a continuación.

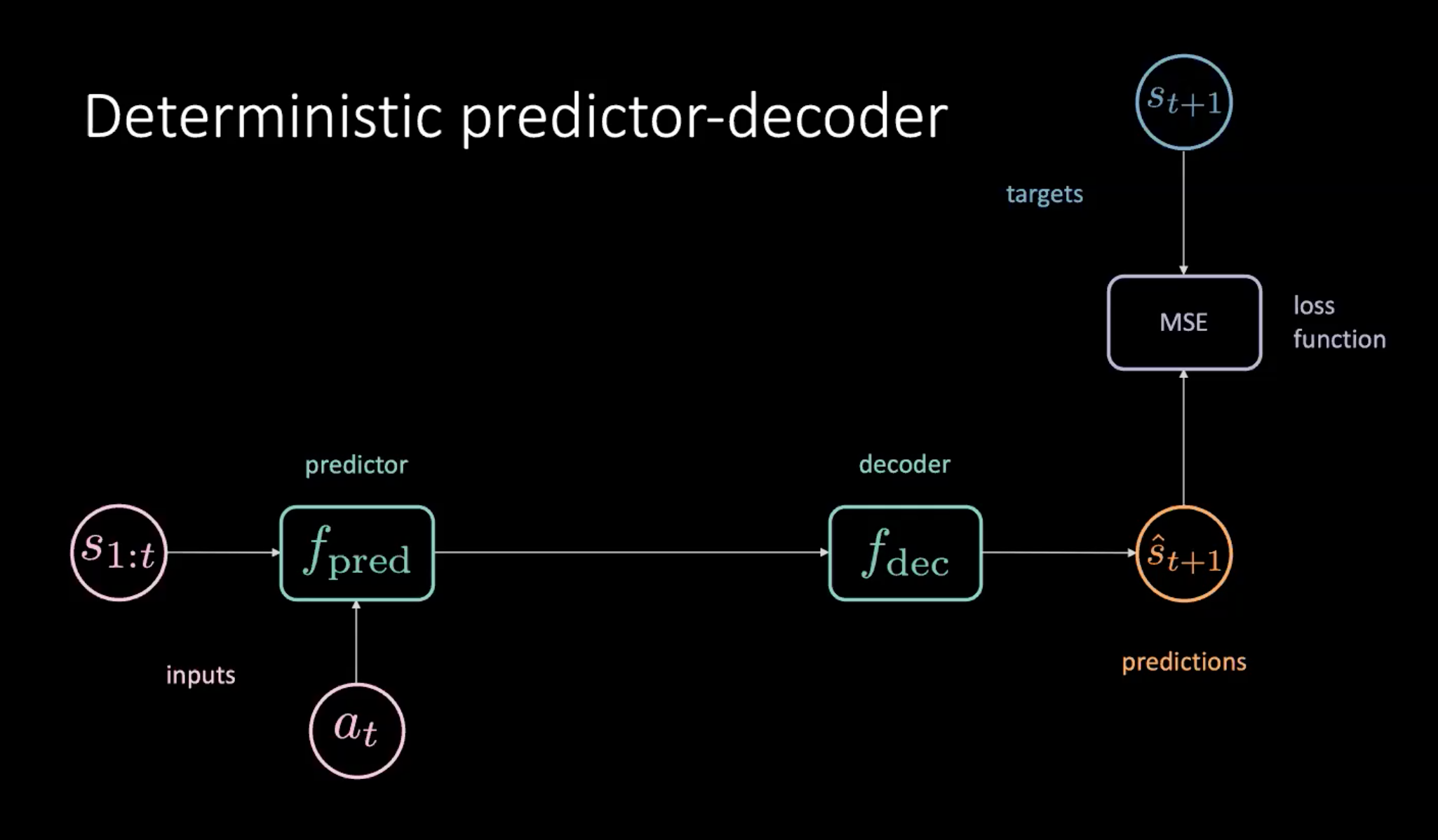
Figura 8: Predictor-decodificador determinista para aprender el modelo del mundo

Como se muestra en la Figura 8, tenemos una secuencia de estados ($s_{1:t}$) y acción ($a_t$) que se proporcionan al módulo predictor. El predictor genera una representación oculta del futuro que se transmite al decodificador. El decodificador está decodificando la representación oculta del futuro y genera una predicción ($\hat s_{t+1}$). Luego entrenamos nuestro modelo minimizando MSE entre predicciones$\hat s_{t+1}$ y objetivo $s_{t+1}$.

Figura 9: Futuro real * vs. * Futuro determinista

¡Por desgracia, esto no funciona!

Vemos que la salida determinista se vuelve muy confusa. Esto se debe a que nuestro modelo promedia todas las posibilidades futuras. Esto se puede comparar con la multimodalidad del futuro discutida un par de clases antes, donde una pluma colocada en el origen se deja caer al azar. Si tomamos el promedio de todas las ubicaciones, nos da la creencia de que la pluma nunca se movió, lo cual es incorrecto.

Podemos abordar este problema introduciendo variables latentes en nuestro modelo.

Red predictiva variacional

Para resolver el problema planteado en la sección anterior, agregamos una variable latente de baja dimensión $z_t$ a la red original que pasa por un módulo de expansión $f_{exp}$ para que coincida con la dimensionalidad.

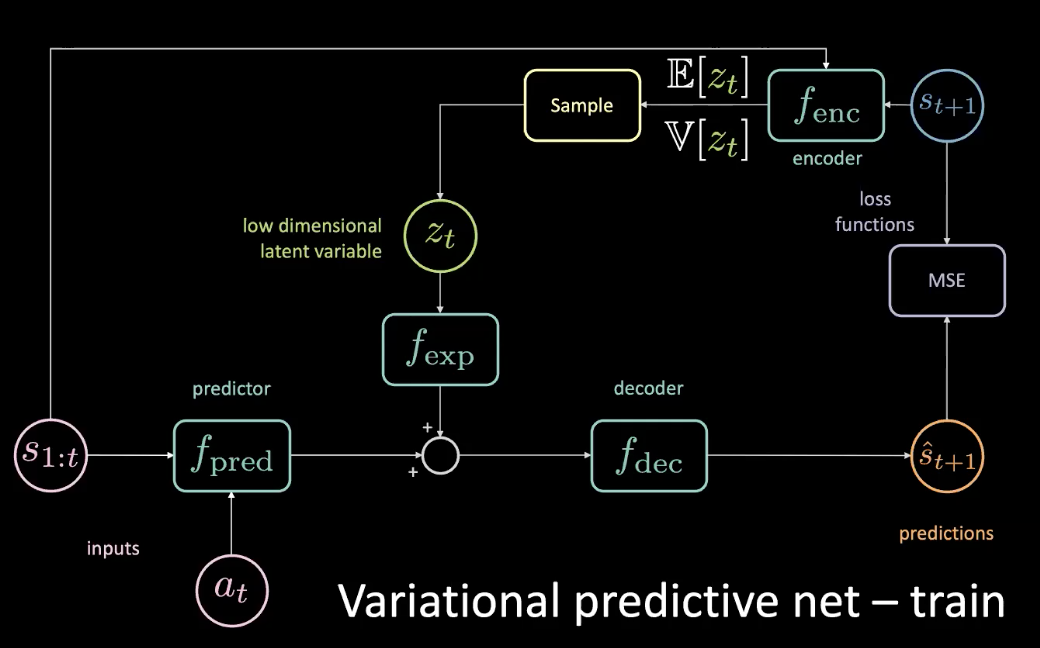
Figura 10: Red predictiva variacional - entrenamiento

Se escoge $z_t$ de manera que el MSE se minimice para una predicción específica. Al ajustar la variable latente, se puede llevar MSE a cero realizando un descenso de gradiente en el espacio latente, pero este es un proceso muy costoso. Entonces, podemos predecir esa variable latente usando un codificador. El codificador toma el estado futuro para darnos una distribución con una media y varianza de las que podemos muestrear $z_t$.

Durante el entrenamiento, podemos averiguar qué está sucediendo en el futuro, obteniendo información de él y usando esa información para predecir la variable latente. Sin embargo, ya en inferencia (prueba) no tenemos acceso al futuro. Arreglamos esto haciendo que el codificador nos dé una distribución posterior lo más cercana posible a la anterior optimizando la divergencia KL.

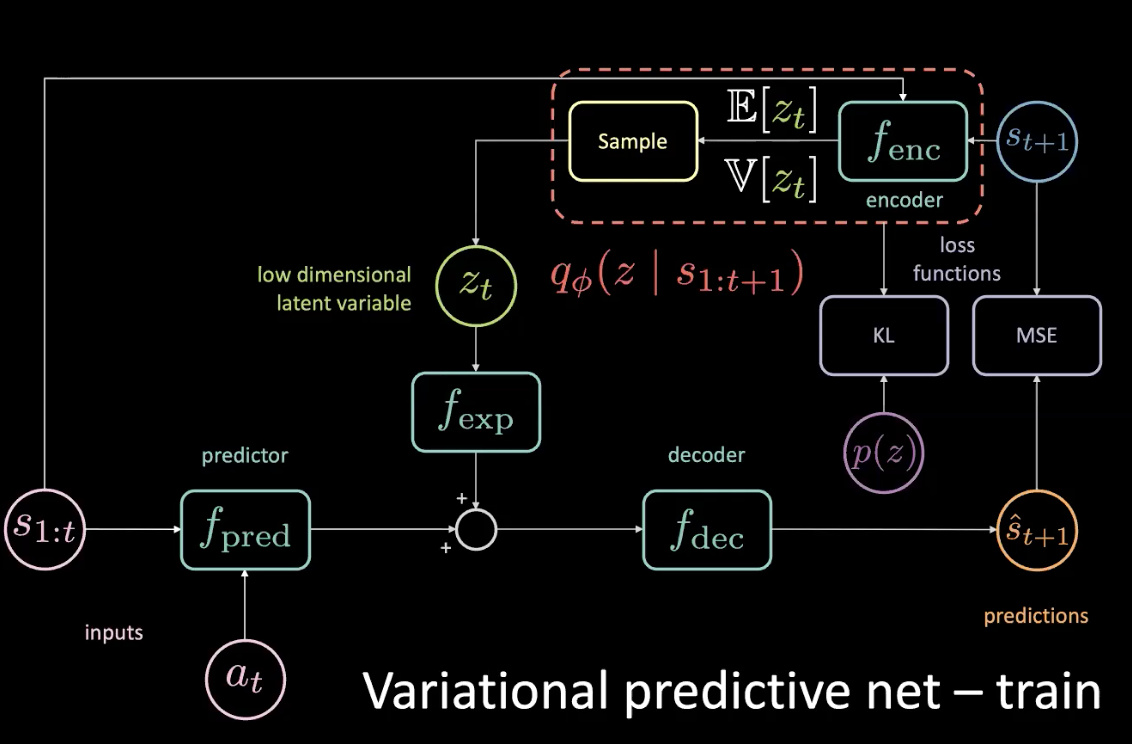
Figura 11: Red predictiva variacional - entrenamiento (con distribución previa)

Ahora, veamos la inferencia: ¿cómo conducimos?

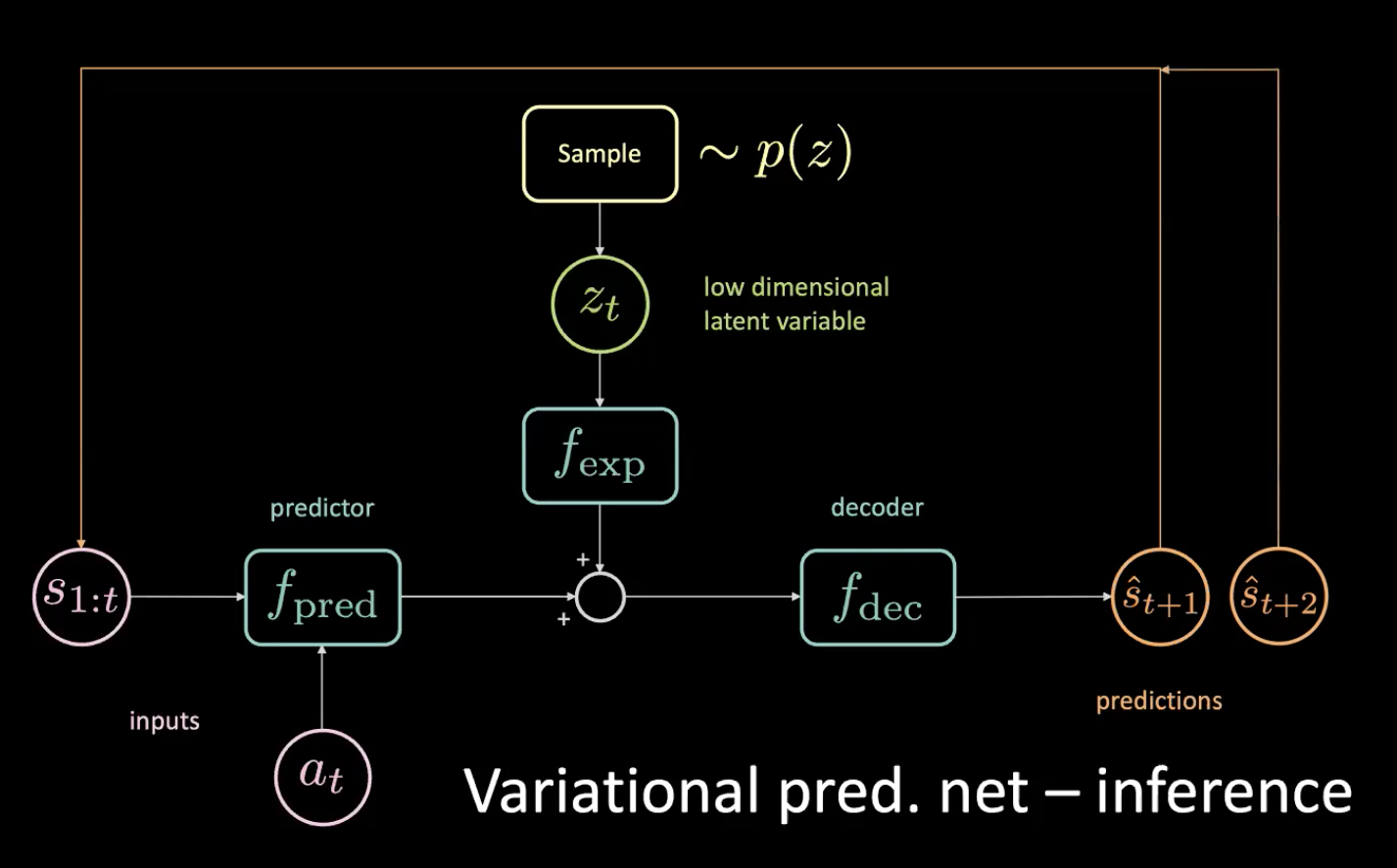
Figura 12: Red predictiva variacional - inferencia

Muestreamos la variable latente de pocas dimensiones $z_t$ ​desde la anterior, obligando al codificador a enviarla hacia esta distribución. Después de obtener la predicción $\hat s_{t+1}$, la devolvemos (en un paso autoregresivo) y obtenemos la siguiente predicción $\hat s_{t+2}$ y seguimos alimentando la red de esta manera.

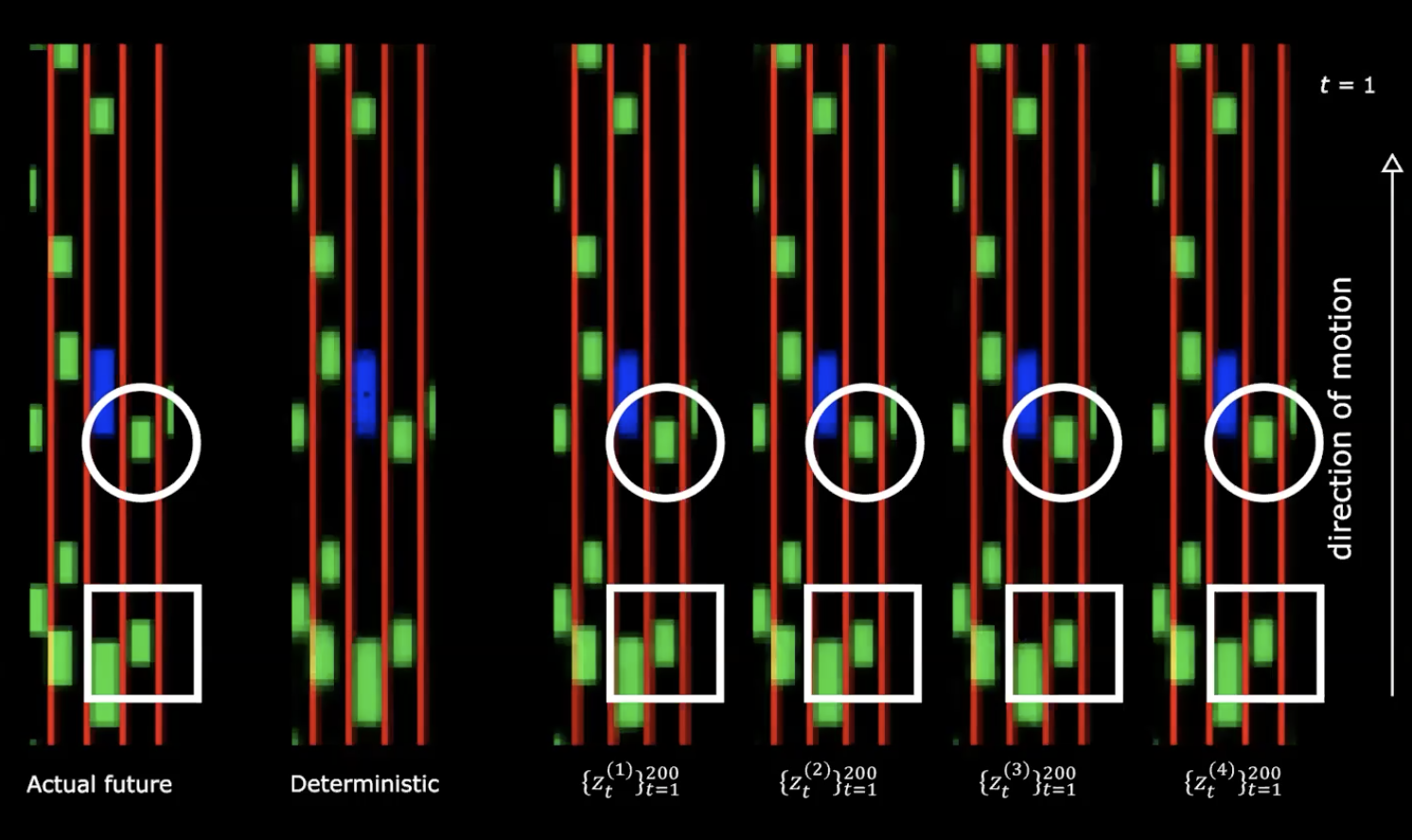
Figura 13: Futuro real *vs.* Determinista

En el lado derecho de la figura anterior, podemos ver cuatro representaciones diferentes de la distribución normal. Comenzamos con el mismo estado inicial y proporcionamos 200 valores diferentes a la variable latente.

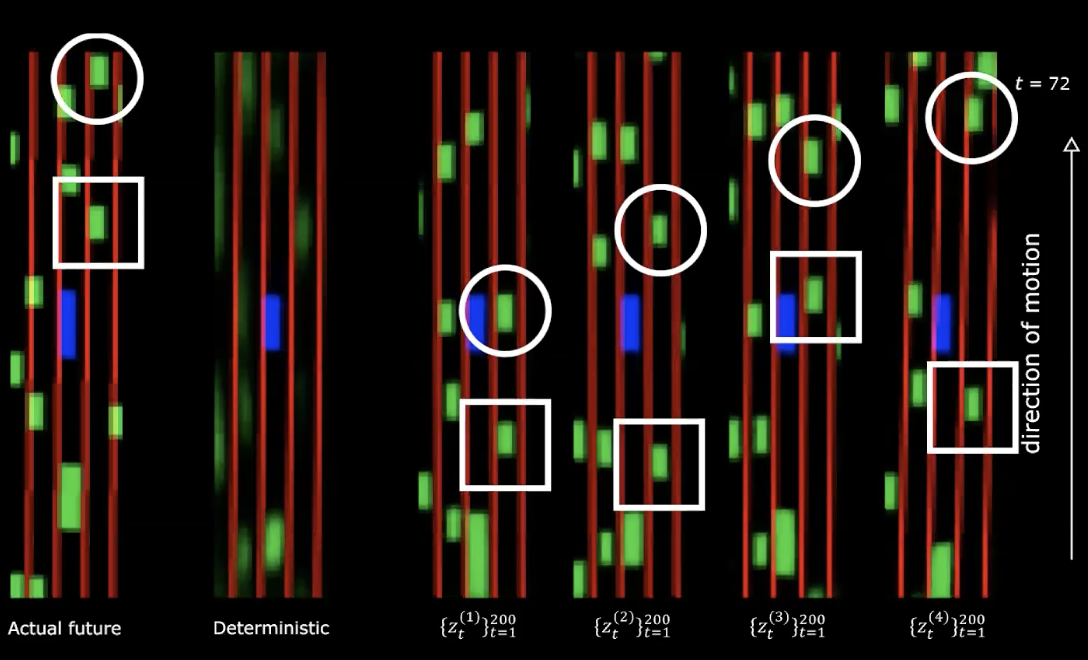
Figura 14: Futuro real * vs.* Determinista - después del movimiento

Podemos notar que proporcionar diferentes variables latentes genera diferentes secuencias de estados con diferentes comportamientos. Lo que significa que tenemos una red que genera el futuro. ¡Muy fascinante!

¿Que sigue?

Ahora podemos usar esta enorme cantidad de datos para entrenar nuestra política optimizando los costos de carril y proximidad descritos anteriormente.

Estos múltiples futuros provienen de la secuencia de variables latentes con que se alimenta a la red. Si se realiza un ascenso de gradiente, en el espacio latente, se intenta aumentar el costo de proximidad para obtener la secuencia de variables latentes de manera que los otros carros manejen hacia nosotros.

Insensibilidad a la acción y dropout latente

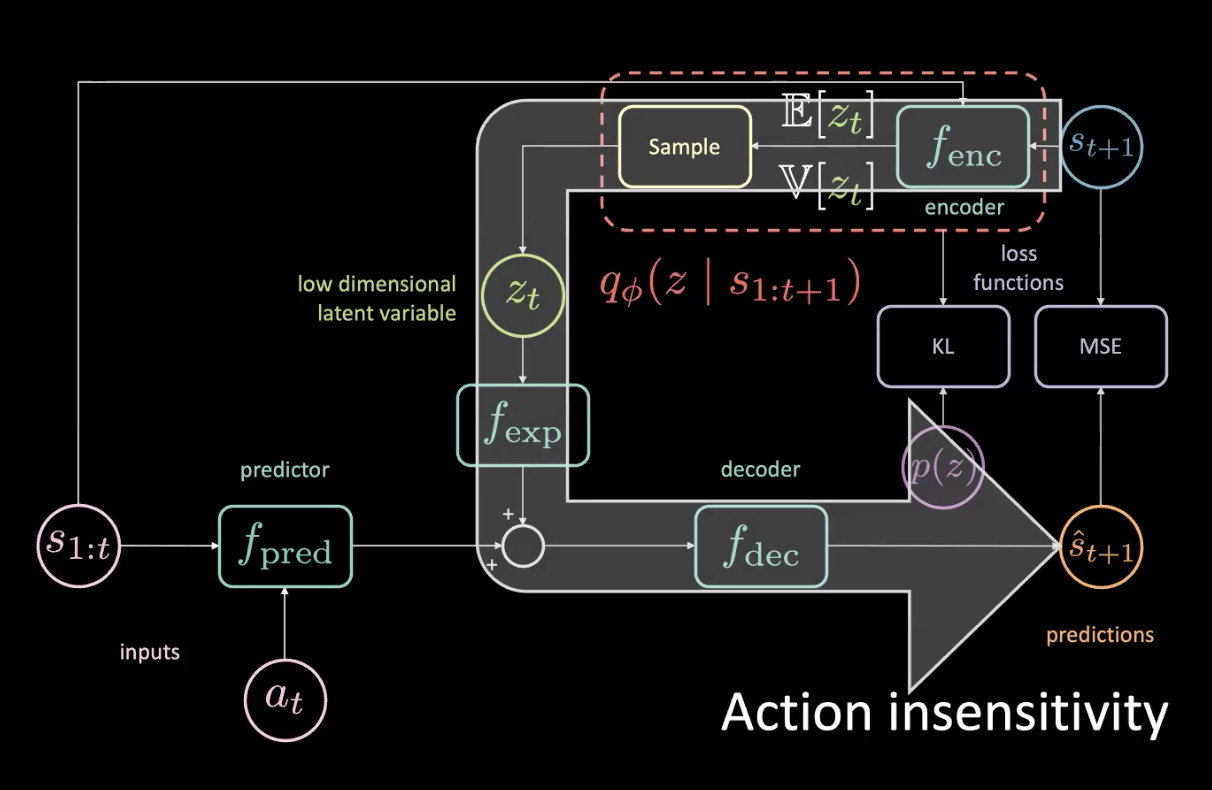
Figura 15: Problemas: insensibilidad a la acción

Dado que en realidad tienes acceso al futuro, si giras a la izquierda aunque sea levemente, todo va a girar a la derecha y eso contribuirá de manera enorme al MSE. La pérdida en el MSE se puede minimizar si la variable latente puede informar a la parte inferior de la red que todo va a girar a la derecha, ¡que no es lo que queremos! Sabemos cuándo todo gira a la derecha ya que es una tarea determinista.

La flecha grande en la Figura 15 significa una fuga de información y, por lo tanto, no es más sensible a la acción actual que se proporciona al predictor.

Figura 16: Problema: insensibilidad a la acción

En la figura 16, en el diagrama de la derecha tenemos la secuencia real de variables latentes (las variables latentes que nos permiten obtener el futuro más preciso) y tenemos la secuencia real de acciones realizadas por el experto. Las dos figuras a la izquierda de ésta han muestreado aleatoriamente las variables latentes, excepto la secuencia real de acciones, por lo que esperamos ver un cambio en la dirección de manejo. El último en el lado izquierdo tiene la secuencia real de acciones de las variables latentes exceptuando las arbitrarias, y podemos ver claramente que el giro provino principalmente de lo latente más que de la acción, lo que codifica la rotación y la acción (que son muestreadas de otras episodios).

¿Cómo arreglar este problema?

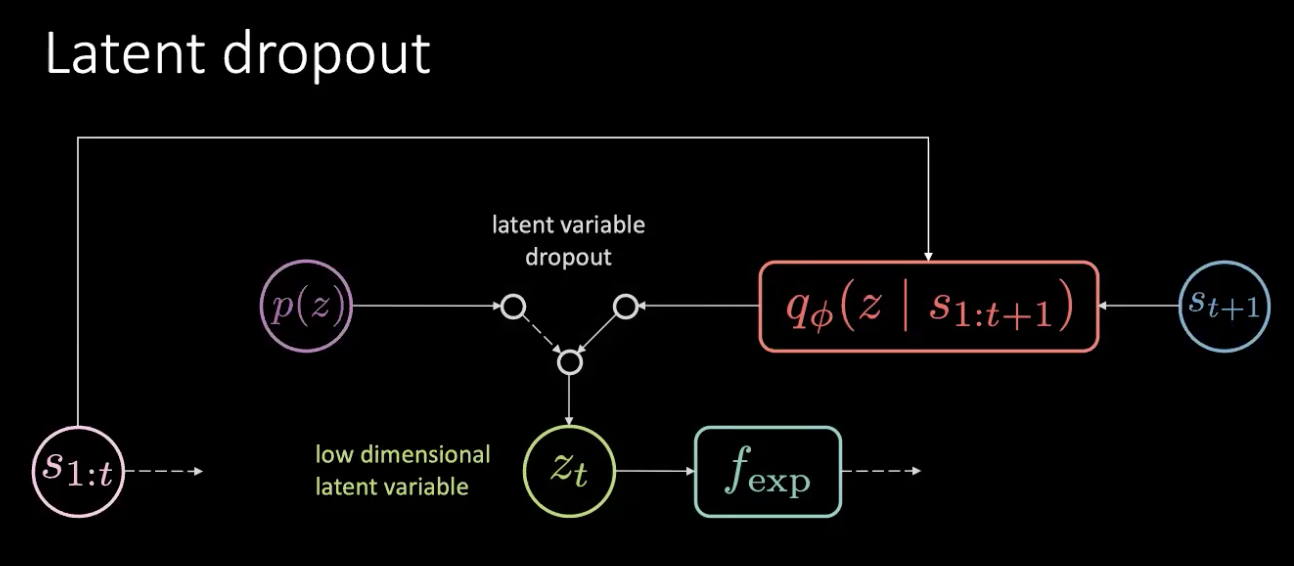
Figura 17: Solución - Dropout Latente

El problema no es una pérdida de memoria, sino una pérdida de información. Solucionamos este problema simplemente eliminando este elemento latente y muestreándolo de la distribución anterior, al azar. No siempre confiamos en la salida del codificador ($f_{enc}$) sino que lo escogemos del anterior. De esta forma, ya no se puede codificar la rotación en la variable latente. De esta manera, la información se codifica en la acción en lugar de en la variable latente.

Figure 18: Rendimiento con dropout latente

En las dos últimas imágenes del lado derecho, vemos dos conjuntos diferentes de variables latentes que tienen una secuencia real de acciones, en donde estas redes han sido entrenadas con el truco del dropout latente. Ahora podemos ver que la rotación ahora está codificada por la acción y ya no por las variables latentes.

Entrenando al agente

En las secciones anteriores, vimos cómo podemos obtener un modelo del mundo, simulando experiencias del mundo real. En esta sección, usaremos este modelo del mundo para entrenar a nuestro agente. Nuestro objetivo es conocer la política para tomar una acción dada la historia de los estados anteriores. Dado un estado $s_t$ (velocidad, posición e imágenes de contexto), el agente realiza una acción $a_t$ (aceleración, freno y dirección), el modelo del mundo genera el siguiente estado y el costo asociado con ese par $(s_t, a_t)$ que es una combinación de costo de proximidad y costo de carril.

Como se discutió en la sección anterior, para evitar predicciones confusas, necesitamos muestrear la variable latente $z_t$ del módulo codificador del estado futuro $s_{t+1}$ o de distribución previa $P(z)$. El modelo del mundo obtiene los estados anteriores $s_{1:t}$​, la acción realizada por nuestro agente y la variable latente $z_t$, para predecir el próximo estado $\hat s_{t+1}$ y el costo. Esto constituye un módulo que se replica varias veces (Figura 19) para darnos la predicción final y la pérdida a optimizar.

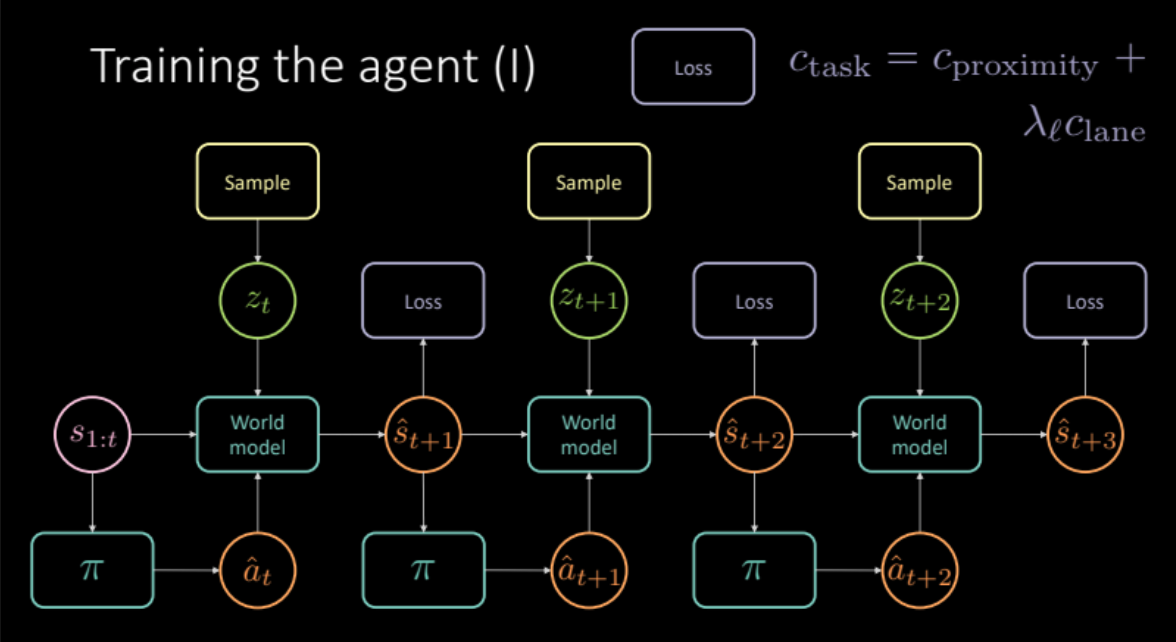
Figura 19: Arquitectura del modelo de tarea específica

Entonces, tenemos nuestro modelo listo. ¡Veamos cómo queda !

Figura 20: Política aprendida: el agente choca o se aleja de la carretera

Por desgracia, esto no funciona. La política entrenada de esta manera no es útil ya que aprende a predecir todo negro, ya que resulta en un costo cero.

¿Cómo podemos abordar este problema? ¿Podemos intentar imitar a otros vehículos para mejorar nuestras predicciones?

Imitando al experto

¿Cómo imitamos a los expertos aquí? Queremos que la predicción de nuestro modelo después de realizar una acción particular desde un estado sea lo más cercana posible al futuro real. Esto actúa como un regularizador experto en nuestro proceso de entrenamiento. Nuestra función de costo ahora incluye tanto el costo específico de la tarea (costo de proximidad y costo de carril) como este término de regularizador experto. Ahora que también estamos calculando la pérdida con respecto al futuro real, tenemos que eliminar la variable latente del modelo porque la variable latente nos da una predicción específica, pero esta configuración funciona mejor si solo trabajamos con la predicción promedio.

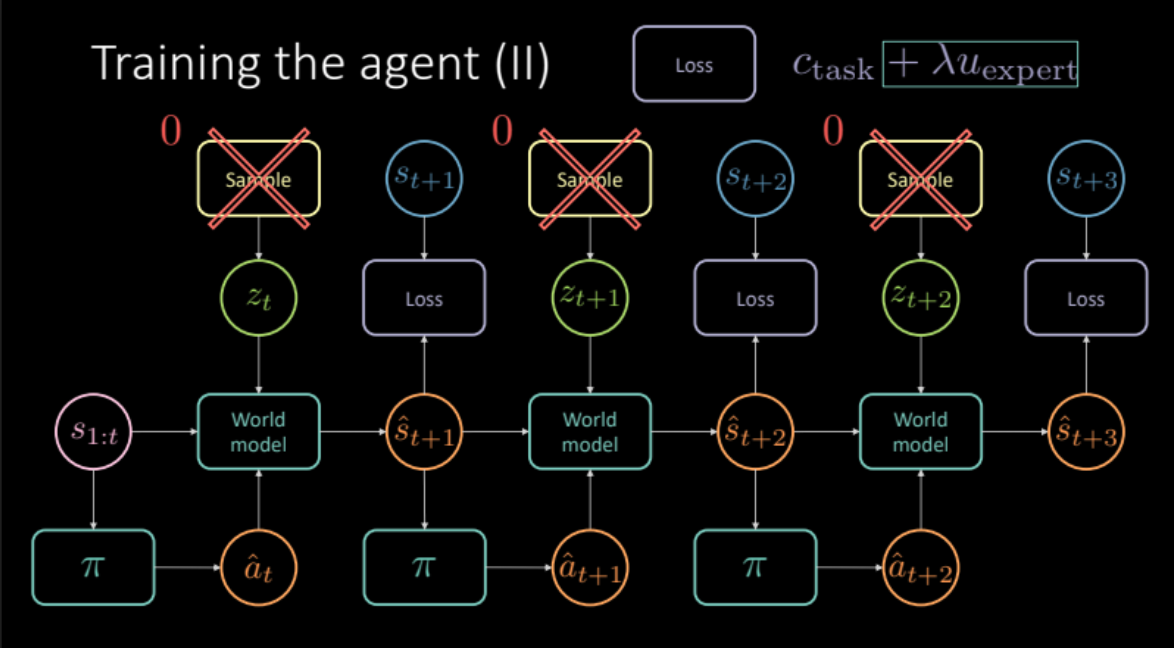
Figura 21: Arquitectura del modelo basado en regularización experta

Entonces, ¿qué tan bien funciona este modelo?

Figura 22: Política aprendida imitando a los expertos

Como podemos ver en la figura anterior, el modelo realmente lo hace increíblemente bien y aprende a hacer muy buenas predicciones. Este fue un aprendizaje de imitación basado en modelos, intentamos modelar a nuestro agente para tratar de imitar a otros.

Pero, ¿podemos hacerlo mejor? ¿Acabamos de entrenar el Autoencoder Variacional para eliminarlo al final?

Resulta que aún podemos mejorar si buscamos minimizar la incertidumbre de las predicciones del modelo a futuro.

Minimizando la incertidumbre del modelo hacia adelante

¿Qué queremos decir con minimizar la incertidumbre del modelo hacia adelante y cómo lo haríamos? Antes de responder a eso, recapitulemos algo que vimos en la práctica de la tercera semana.

Si entrenamos varios modelos con los mismos datos, todos esos modelos coinciden en los puntos de la región de entrenamiento (mostrados en rojo), lo que da como resultado una varianza cero en la región de entrenamiento. Pero a medida que nos alejamos de la región de entrenamiento, las trayectorias de las funciones de pérdida de estos modelos comienzan a divergir y la varianza aumenta. Esto se muestra en la figura 23. Pero como la varianza es diferenciable, podemos ejecutar un descenso de gradiente sobre la varianza para minimizarla.

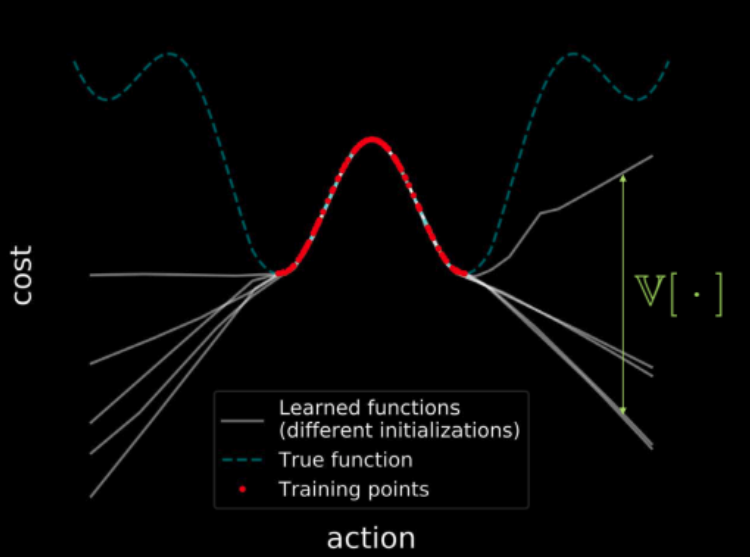
Figura 23: Visualización de costos en todo el espacio de entrada

Volviendo a nuestra discusión, observamos que aprender una política utilizando solo datos de observación es un desafío porque la distribución de estados que se produce durante la ejecución puede ser diferente de lo observado durante la fase de entrenamiento. El modelo del mundo puede hacer predicciones arbitrarias fuera del dominio en el que fue entrenado, lo que puede resultar erróneamente en un bajo costo. Entonces, la red de políticas puede aprovechar estos errores en el modelo de dinámica y producir acciones que conduzcan a estados erróneamente optimistas.

Para abordar esto, proponemos un costo adicional que mide la incertidumbre del modelo de dinámica sobre sus propias predicciones. Esto se puede calcular pasando la misma entrada y acción a través de varias máscaras de dropout diferentes y calculando la varianza entre las diferentes salidas. Esto alienta a la red de políticas a producir solo acciones para las que el modelo hacia adelante tiene confianza.

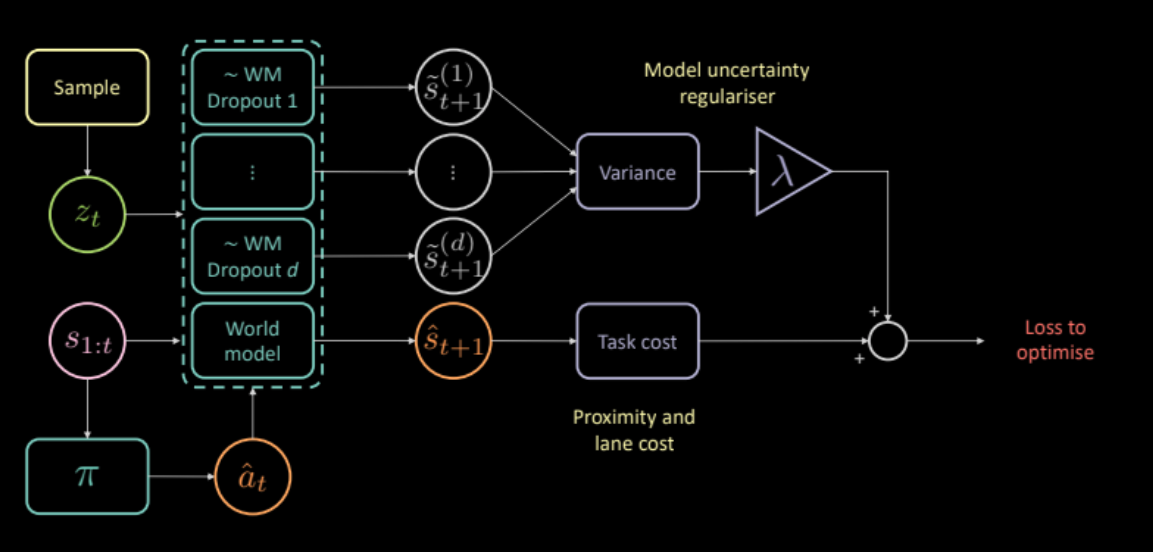
Figura 24: Arquitectura del modelo basado en regularizador de incertidumbre

Entonces, ¿el regularizador de incertidumbre nos ayuda a aprender mejores políticas?

Sí lo hace. La política aprendida de esta manera es mejor que los modelos anteriores.

Figura 25: Política aprendida basada en regularizador de incertidumbre

Evaluación

La Figura 26 muestra qué tan bien aprendió nuestro agente a conducir en un tráfico denso. El carro amarillo es el conductor original, el azul es nuestro agente y todos los carros verdes son ciegos para nosotros (no se pueden controlar).

Figura 26: Rendimiento del modelo con regularizador de incertidumbre