Funciones de Pérdida (cont.) y Funciones de Pérdida para Modelos Basados en Energía

Pérdida de Entropía Cruzada Binaria (BCE) - nn.BCELoss()

Esta pérdida es un caso especial de la entropía cruzada para cuando solo tienes dos clases así que se puede reducir a una función más simple. Se puede usar para medir el error de reconstrucción; por ejemplo, en un auto-encoder. Esta fórmula asume que $x$ e $y$ son probabilidades, así que están estrictamente en el rango de entre 0 y 1.

Pérdida de Divergencia Kullback-Leibler - nn.KLDivLoss()

Esta es una función de pérdida simple para cuando tu objetivo es una distribución one-hot (es decir, $y$ es una categoría). De nuevo, se asume que $x$ e $y$ son probabilidades. Tiene la desventaja de que no está combinada con una softmax o una log-softmax, por lo que puede tener problemas de estabilidad numérica.

Pérdida BCE con Logits - nn.BCEWithLogitsLoss()

Esta versión de la entropía cruzada binaria recibe puntajes que no han pasado por la función softmax, así que no asume que x esté entre 0 y 1. Después el resultado pasa por una sigmoide para asegurar que esté en ese rango. La función de pérdida tiende a ser más numéricamente estable cuando se combina de esta manera.

Pérdida de Ránking de Margen - nn.MarginRankingLoss()

Las pérdidas de margen son una categoría de pérdidas importantes. Si tienes dos entradas, esta función de pérdida indica que quieres que una de las entradas sea más grande que la otra por al menos un margen. En este caso $y$ es una variable binaria $\in { -1, 1}$. Puedes pensar en las dos entradas como en puntajes de dos categorías. Vas a querer que el puntaje para la categoría correcta sea más grande que el puntaje para las categorías incorrectas por lo menos por algún margen. Como la pérdida de bisagra; si $y*(x_1-x_2)$ es más grande que el margen, el costo es 0. Si es más pequeño, el costo incrementa de forma lineal. Si fueses a utilizar esto para clasificar, tendrías que $x_1$ es el puntaje de la respuesta correcta y $x_2$ es el puntaje de la respuesta incorrecta con puntaje más alto en el mini-lote. Si se utiliza en modelos basados en energía (los discutiremos más adelante), esta función de pérdida empuja hacia abajo sobre la respuesta correcta $x_1$ y hacia arriba sobre la respuesta incorrecta $x_2$.

Pérdida de Margen Trilliza - nn.TripletMarginLoss()

Esta pérdida se usa para medir la similitud relativa entre muestras. Por ejemplo, puedes pasar dos imágenes con la misma categoría por una CNN y obtener dos vectores. Vas a querer que la distancia entre los dos vectores sea lo más pequeña posible. Si pasas dos imágenes con diferentes categorias por una CNN, vas a querer que la distancia entre esos vectores sea lo más grande posible. Esta función de pérdida intenta hacer que la primera distancia sea 0 y la segunda distancia sea más grande que algún margen. Sin embargo, la única cosa que importa es que la distancia entre el par de imágenes de la misma clase sea más pequeña que la distancia entre el par de imágenes de clase distinta.

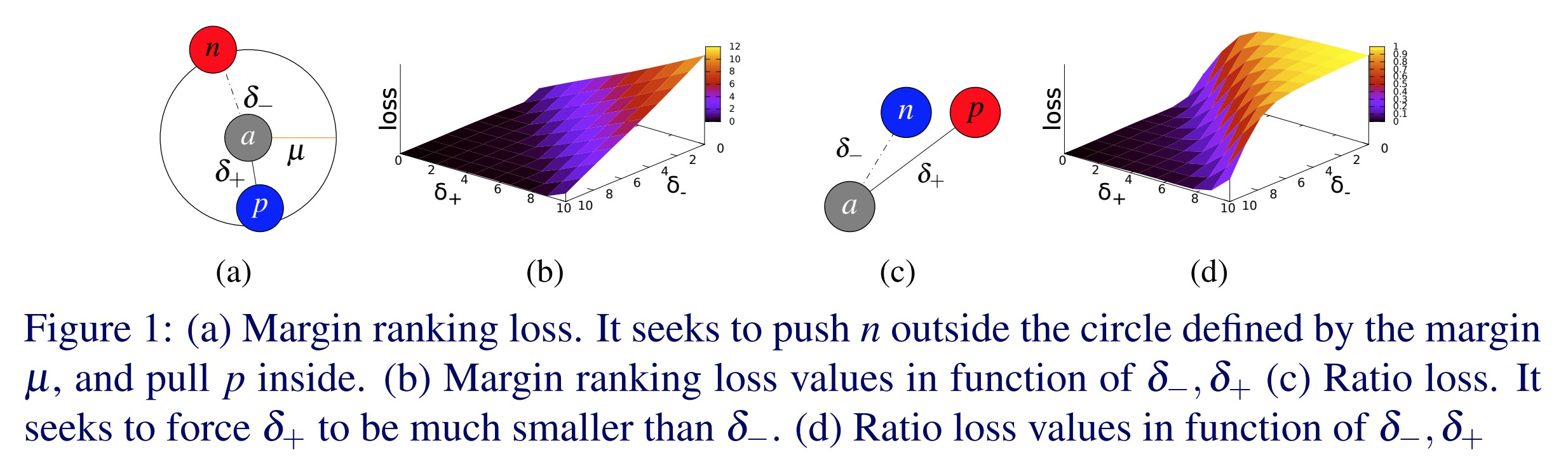
Fig. 1: Pérdida de Margen Trilliza

Esta función se usó originalmente para entrenar un sistema de búsqueda de imágenes para Google. En ese entonces, escribías una consulta en Google y Google codificaba esa consulta como un vector. Luego, se comparaba ese vector con un montón de vectores de imágenes que se habían indexado anteriormente. Google entonces recuperaba las imágenes más cercanas al vector.

Pérdida Soft Margen - nn.SoftMarginLoss()

Esta función crea un criterio que optimiza la pérdida logística para clasificación de dos clases entre un tensor de entrada $x$ y un tensor objetivo $y$ (que contiene 1 o -1).

• Esta es una versión softmax de la pérdida de margen. Tienes un puñado de ejemplos positivos y de ejemplos negativos que quieres pasar por una softmax. Esta función de pérdida entonces intenta hacer que el $\text{exp}(-y[i]*x[i])$ para el $x[i]$ correcto sea más pequeño que para cualquier otro.
• Esta función de pérdida intenta jalar los valores positivos de $y[i]*x[i]$ para acercarlos y alejar los valores negativos, pero al contrario que el margen duro, tiene un efecto continuo y de decadencia exponencial sobre la función de pérdida.

Pérdida de Bisagra Multi-Clase - nn.MultiLabelMarginLoss()

Esta pérdida basada en margen permite que las distintas entradas tengan cantidades de objetivos variables. En este caso tienes varias categorías para las cuales quieres puntajes altos y se suma la pérdida de bisagra para todas las categorías. Para modelos basados en energía, esta función de pérdida empuja hacia abajo sobre las categorías deseadas y hacia arriba sobre las no-deseadas.

Perdida de Embedding de Bisagra - nn.HingeEmbeddingLoss()

La pérdida de embedding de bisagra se usa para aprendizaje semi-supervisado al medir si dos entradas son similares o disímiles. Acerca las cosas que son similares y separa las cosas que son disímiles. La variable $y$ indica si la pareja de puntajes debe ir en cierta dirección. Usando una pérdida de bisagra, el puntaje es positivo si $y$ es 1 y algún margen $\Delta$ si $y$ es -1.

Pérdida de Embedding de Coseno - nn.CosineEmbeddingLoss()

Esta pérdida se usa para medir si dos entradas son similares o disímiles, usando la distancia de coseno, y a menudo se utiliza para aprender embeddings no-lineales o para aprendizaje semi-supervisado.

• Puesto de otra manera, 1 menos el coseno del ángulo entre los dos vectores es básicamente la distancia Euclidiana normalizada.
• La ventaja de esto es que siempre que tengas dos vectores y quieras hacer la distancia entre ellos lo más grande posible, es muy fácil hacer que la red logre esto haciendo que los vectores sean muy largos. Por supuesto, esto no es óptimo. No quieres que el sistema haga los vectores grandes sino que los rote en la dirección correcta para que los puedas normalizar y calcular la distancia Euclidiana normalizada.
• Para los casos positivos, esta pérdida intenta hacer que los vectores se alineen tanto como sea posible. Para las parejas negativas, se intenta que el coseno sea más pequeño que un margen particular. El margen aquí debería ser algún valor positivo pequeño.
• En un espacio de alta dimensionalidad, hay una área muy grande cerca del ecuador de la esfera. Tras normalizar, todos tus puntos ahora estarán normalizados sobre la esfera. Lo que quieres es que las muestras que son semánticamente parecidas estén cerca. Las muestras que son disímiles deberían ser ortogonales. No quieres que sean opuestas entre sí porque solo hay un punto en el polo opuesto. Más bien, sobre el ecuador hay una cantidad muy grande de espacio así que vas a querer que el margen sea algún valor positivo pequeño para que puedas tomar ventaja de toda esta área.

Pérdida de Clasificación Temporal Conexionista (CTC) - nn.CTCLoss()

Calcula la pérdida entre una serie de tiempo continua (no-segmentada) y una secuencia objetivo. La pérdida CTC realiza una suma sobre la probabilidad de los posibles alineamientos de la entrada al blanco, que produce un valor de pérdida que es diferenciable con respecto a cada nodo de entrada.

• Se asume que el alineamiento entre la entrada y la salida es de «muchos-a-uno», lo que limita la longitud de la secuencia objetivo tal que sea menor o igual a la longitud de la secuencia de entrada.
• Es útil cuando tu salida es una secuencia de vectores, que se corresponden con puntajes de categorías.

Fig. 2: Pérdida CTC para reconocimiento del habla

Ejemplo de aplicación: Sistema de reconocimiento del habla

• Goal: Predecir una palabra que se pronuncia cada 10 milisegundos.
• Cada palabra se representa como una secuencia de sonidos.
• Dependiendo de la velocidad de habla de una persona, diferentes longitudes de los sonidos podrían mapearse a la misma palabra.
• Encontrar el mejor mapeo de la secuencia de entrada a la secuencia de salida. Un buen método para esto es usar programación dinámica para encontrar el camino de costo mínimo.

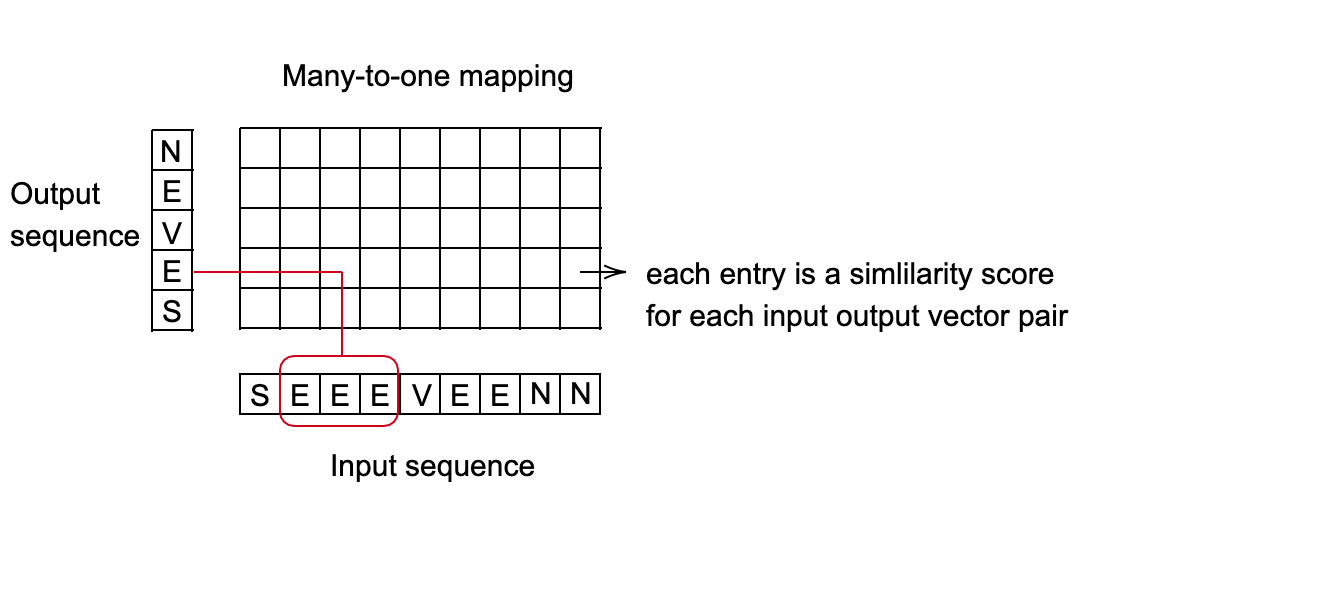
Fig. 3: Configuración para mapeo de muchos-a-uno.

Modelos Basados en Energía (Parte IV) - Función de Pérdida

Arquitectura y Funcional de Pérdida

Familia de funcionales de energía: $\mathcal{E} = {E(W,Y, X) : W \in \mathcal{W}}$.

Conjunto de entrenamiento: $S = {(X^i, Y^i): i = 1 \cdots P}$

Funcional de pédida: $\mathcal{L} (E, S)$

• Funcional quiere decir función de otra función. En nuestro caso, el funcional $\mathcal{L} (E, S)$ es una función de la función de energía $E$.
• Ya que $E$ se parametriza por medio de $W$, podemos convertir el funcional en una función de pérdida de $W$: $\mathcal{L} (W, S)$
• Mide la calidad de una función de energía sobre el conjunto de entrenamiento
• Es invariante a permutaciones y repeticiones de las muestras

Entrenamiento: $W^* = \min_{W\in \mathcal{W}} \mathcal{L}(W, S)$.

Forma del funcional de pérdida:

• $L(Y^i, E(W, \mathcal{Y}, X^i))$ es la pérdida por cada muestra.
• $Y^i$ es la respuesta deseada, puede ser una categoría o una imagen entera, etc.
• $E(W, \mathcal{Y}, X^i)$ es la superficie de energía para un $X_i$ dado a medida que $Y$ varía.
• $R(W)$ es un regularizador.

Diseñar una buena Función de Pérdida

Empujar hacia abajo sobre la energía de la respuesta correcta.

Empujar hacia arriba sobre las energías de las respuestas incorrectas, en particular si son más pequeñas que la correcta.

Ejemplos de Funciones De Pérdida

Pérdida de Energía

Esta pérdida simplemente empuja hacía abajo sobre la energía de la respuesta correcta. Si la red no se diseña de forma apropiada, podría terminar con una función de energía mayormente plana puesto que intentas hacer que la energía de la respuesta correcta sea pequeña pero no empujas la energía hacia arriba en otras partes. Por lo tanto, el sistema podría colapsar.

Pérdida de Log-Verosimilitud Negativa

Esta función de pérdida empuja hacía abajo sobre la energía de la respuesta correcta a la vez que empuja hacia arriba las energías de todas las respuestas en proporción a sus probabilidades. Esto reduce la pérdida del perceptrón cuando $\beta \rightarrow \infty$. Se ha utilizado por mucho tiempo en varias comunidades para entrenamiento discriminativo con salidas estructuradas.

Un modelo probabilístico es un EBM en el cual:

• La energía se puede integrar sobre Y (la variable a predecir)
• La pérdida es la log-verosimilitud negativa

Pérdida de Perceptrón

Muy parecida a la pérdida de perceptrón de hace 60+ años, y siempre es positiva ya que el mínimo también se toma sobre $Y^i$, así que $E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$. El mismo cálculo muestra que devuelve exactamente cero solo cuando $Y^i$ es la respuesta correca.

Esta pérdida hace que la energía de la respuesta correcta sea pequeña, y al mismo tiempo, hace que la energía para todas las otras respuestas sea lo más grande posible. Sin embargo, esta pérdida no evita que la función le de el mismo valor a todas las respuestas incorectas $Y^i$, así que en este aspecto, es una función de pérdida mala para sistemas no-lineales. Para mejorar esta función de pérdida, definimos la respuesta incorrecta más transgresora.

Pérdida de Margen Generalizado

Respuesta incorrecta más transgresora: caso discreto Sea $Y$ una variable discreta. Entonces para una muestra de entrenamiento $(X^i,Y^i)$, la respuesta incorrecta más transgresora $\bar Y^i$ es la respuesta que tiene la energía más baja entre todas las respuestas posibles que son incorrectas:

Respuesta incorrecta más transgresora: caso continuo Sea $Y$ una variable continua. Entonces para una muestra de entrenamiento $(X^i,Y^i)$, la respuesta incorrecta más transgresora $\bar Y^i$ es la respuesta que tiene la energía más baja entre todas las respuestas que están por lo menos a un valor $\epsilon$ de distancia de la respuesta correcta:

En el caso discreto, la respuesta incorrecta más transgresora es la respuesta incorrecta que tiene la energía más pequeña. En el caso continuo, la energía para $Y$ extremadamente cerca de $Y^i$ debería estar cerca de $E(W,Y^i,X^i)$. Además, el $\text{argmin}$ evaluado sobre $Y$ distinto de $Y^i$ sería 0. Como resultado, escogemos una distancia $\epsilon$ y decidimos que solo los $Y$ por lo menos a una distancia $\epsilon$ de $Y_i$ deberían ser considerados como la «respuesta incorrecta». Esto es porque la optimización solo se hace sobre $Y$”s que estén a una distancia de al menos $\epsilon$ de $Y^i$.

Si la función de energía es capaz de asegurar que la energía de la respuesta incorrecta más transgresora sea más alta que la energía de la respuesta correcta por algún margen, entonces esta función de energía debería funcionar bien.

Ejemplos de Funciones De Pérdida Generalizadas

Pérdida de Bisagra

Donde $\bar Y^i$ es la respuesta incorrecta más transgresora. Esta pérdida obliga a que la diferencia entre la respuesta correcta y la respuesta incorrecta más transgresora sea por lo menos de $m$.

Fig. 4: Pérdida de Bisagra

Q: ¿Cómo escoges $m$?

A: Es arbitrario, pero afecta los pesos de la última capa.

Pérdida Logarítmica

Se puede interpretar como una pérdida de bisagra «suave». En vez de ajustar la diferencia entre la respuesta correcta y la respuesta incorrecta más transgresora con una bisagra, ahora se ajusta con una bisagra suave. Esta pérdida intenta forzar un «margen infinito», pero debido a la degradación exponencial de la pendiente, esto no ocurre.

Fig. 5: Pérdida Logarítmica

Pérdida Cuadrada-Cuadrada

Esta pérdida intenta combinar el cuadrado de la energía con una bisagra al cuadrado. Esta combinación intenta minimizar la energía y forzar un margen de al menos $m$ sobre la respuesta incorrecta más transgresora. Esto es muy similar a la pérdida usada en las redes Siamesas.

Otras Pérdidas

Hay muchas otras. Aquí hay un resumen de algunas funciones de pérdida buenas y malas.

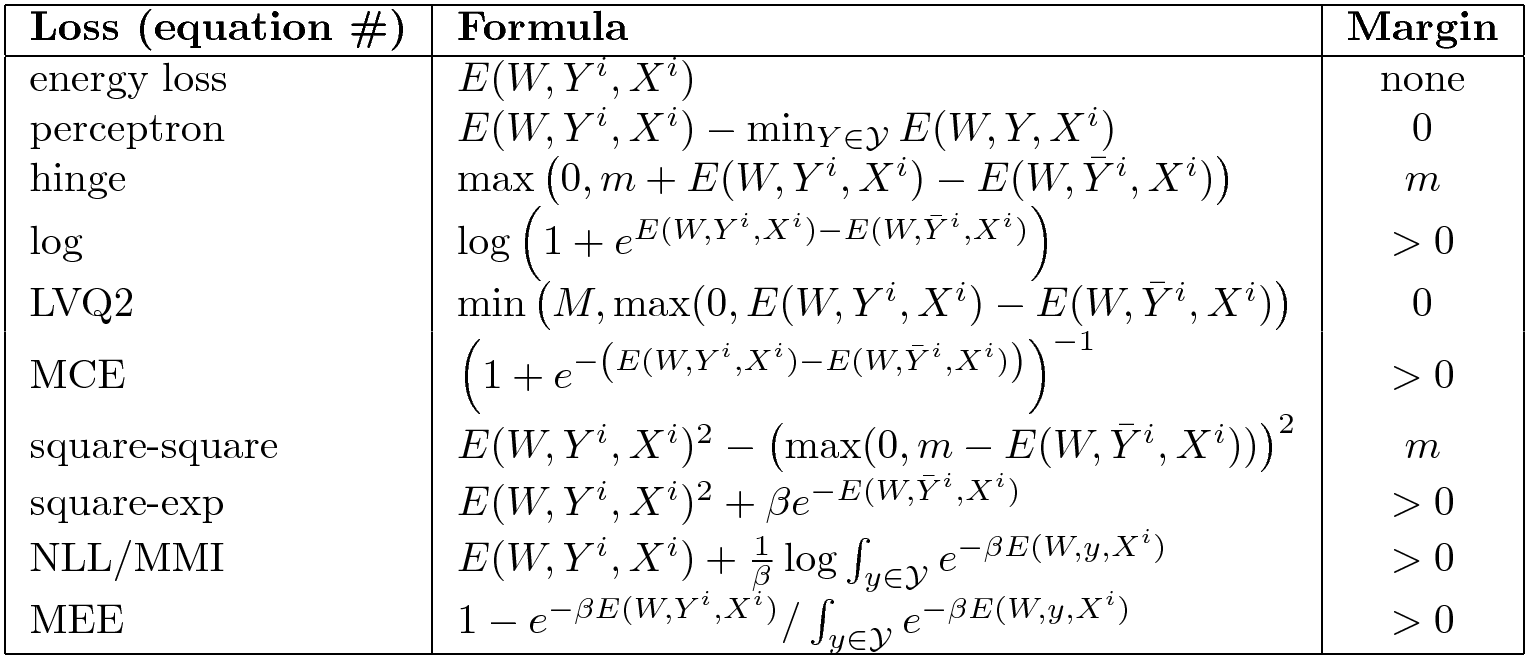
Fig. 6: Selección de funciones de pérdida para EBMs

La columna de la derecha indica si la función de pérdida obliga a que haya un margen. La típica pérdida de energía no empuja hacia arriba en ninguna parte, así que no tiene un margen. La pérdida de energía no funciona para todos los problemas. La pérdida de perceptrón funciona si tienes una parametrización lineal de tu energía pero no en general. Algunas de ellas tienen un margen finito como la pérdida de bisagra, y otras tienen un margen infinito, como la bisagra suave.

Q: ¿Cómo se encuentra la respuesta incorrecta más transgresora $\bar Y_i$ en el caso continuo?

A: Quieres empujar hacia arriba en un punto que esté lo suficientemente lejos de $Y^i$, porque si está muy cerca, los parámetros podrían no moverse mucho ya que la función definida por una red neuronal es «rígida». Pero en general, esto es difícil y es el problema que intentan resolver los métodos que seleccionan muestras contrastivas. No hay una única forma correcta de hacerlo.

Una forma ligeramente más general de las pérdidas contrastivas de tipo bisagra es:

Asumimos que $Y$ es discreta, pero si fuese continua, la suma se remplazaría por una integral. Aquí, $E(W, Y^i,X^i)-E(W,y,X^i)$ es la diferencia entre $E$ evaluado en la respuesta correcta y en alguna otra respuesta. $C(Y^i,y)$ es el margen, y generalmente es una medición de la distancia entre $Y^i$ y $y$. La motivación es que la cantidad por la que queremos empujar hacia arriba sobre una muestra incorrecta $y$ debería depender de la distancia entre $y$ y la muestra correcta $Y_i$. Esta puede ser una pérdida difícil de optimizar.