Funciones de activación y de costo (parte 1)
🎙️ Yann LeCunFunciones de activación
En la clase de hoy, vamos a repasar algunas funciones de activación importantes y sus implementaciones en PyTorch. Estas funciones vienen de varios artículos en los que se asegura que funcionan mejor para problemas específicos.
ReLU - nn.ReLU()
\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]
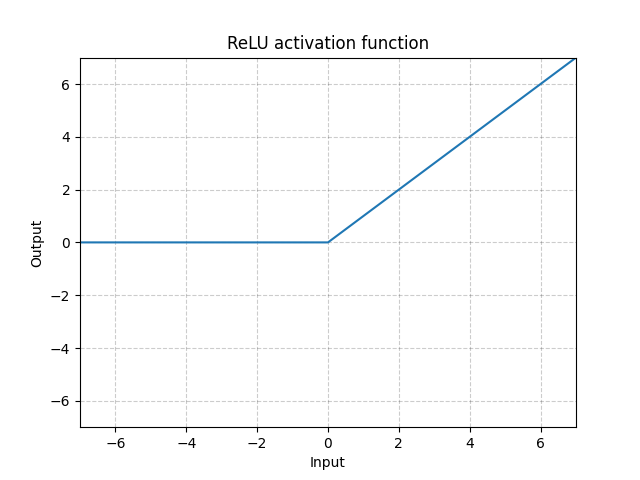
Fig. 1: ReLU
RReLU - nn.RReLU()
Hay variaciones de la ReLU. La ReLU Aleatoria (RReLU, por sus siglas en inglés) se define de la siguiente manera:
\[\text{RReLU}(x) = \begin{cases} x, & \text{si} x \geq 0\\ ax, & \text{en otro caso} \end{cases}\]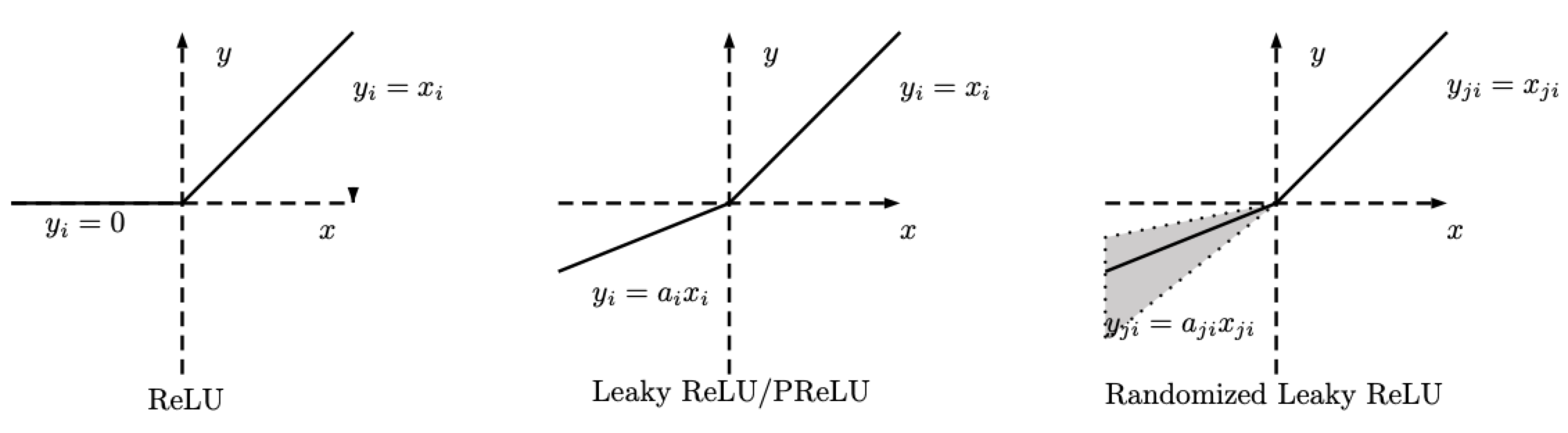
Fig. 2: ReLU, Leaky ReLU/PReLU, RReLU
Recuerda que para la RReLU, $a$ es una variable aleatoria que se muestrea constantemente a partir de un rango dado durante el entrenamiento, y se mantiene fija durante las pruebas. Para PReLU, $a$ es además un parámetro aprendido. Para la Leaky ReLU, $a$ es un valor fijo.
LeakyReLU - nn.LeakyReLU()
\[\text{LeakyReLU}(x) = \begin{cases}
x, & \text{si} x \geq 0\\
a_\text{pendiente negativa}x, & \text{en otro caso}
\end{cases}\]
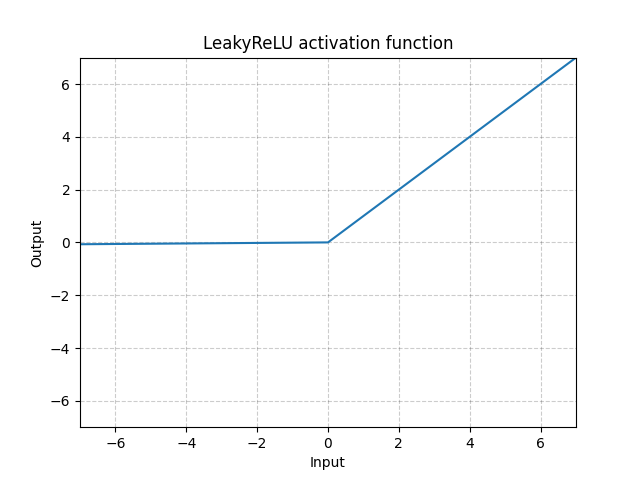
Fig. 3: LeakyReLU
Aquí, $a$ es un parámetro fijo. La parte interior de la ecuación evita el problema de las ReLU muertas, que se refiere al problema que ocurre cuando las neuronas ReLU se vuelven inactivas y solo retornan 0 para cualquier valor de entrada. Por tanto, su gradiente es 0. Al usar una pendiente negativa, se permite que la red haga propagación hacia atrás y aprenda algo útil.
La LeakyReLU es necesaria para las redes neuronales delgadas, en las que es casi imposible hacer que los gradientes fluyan hacia atrás con la ReLU por defecto. Con la LeakyReLU, la red puede seguir teniendo gradientes incluso cuando estamos en la región en la que todo se vuelve cero.
PReLU - nn.PReLU()
\[\text{PReLU}(x) = \begin{cases}
x, & \text{si} x \geq 0\\
ax, & \text{en otro caso}
\end{cases}\]
Aquí, $a$ es un parámetro que se puede aprender.
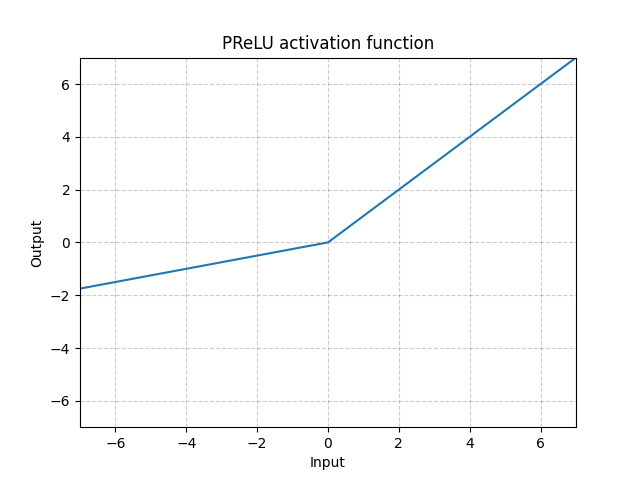
Fig. 4: ReLU
Las funciones de activación descritas arriba (es decir, ReLU, LeakyReLU y PReLU) son invariantes de escala.
Softplus - Softplus()
\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]
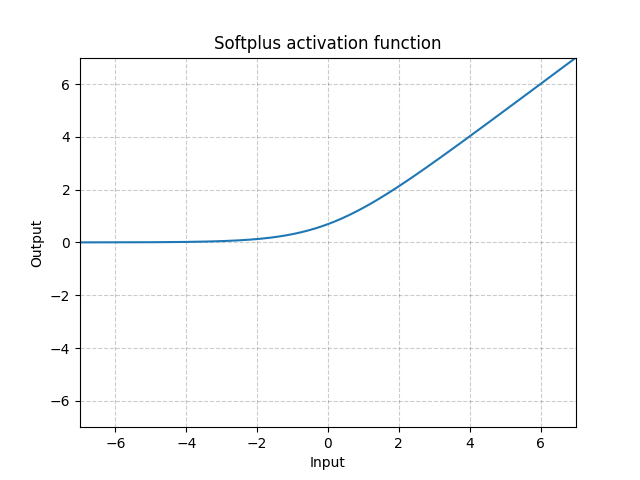
Fig. 5: Softplus
La Softplus es una aproximación suave de la función ReLU y puede ser usada para restringir la salida de una neurona para que siempre sea positiva.
La función se volverá más como la ReLU, si el $\beta$ se vuelve más y más grande.
ELU - nn.ELU()
\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1)\]
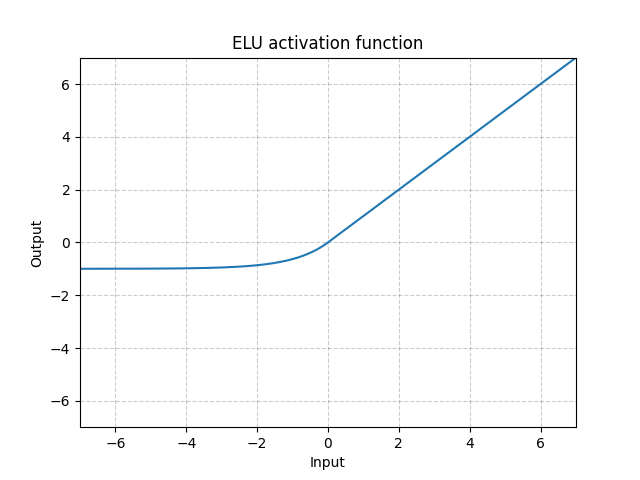
Fig. 6: ELU
Al contrario que la ReLU, puede ir debajo de 0, lo que permite que el sistema tenga una salida promedio de 0. Por lo tanto, el modelo puede converger más rápido. Y sus variaciones (CELU, SELU) son simplemente versiones con parametrizaciones diferentes.
CELU - nn.CELU()
\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1)\]
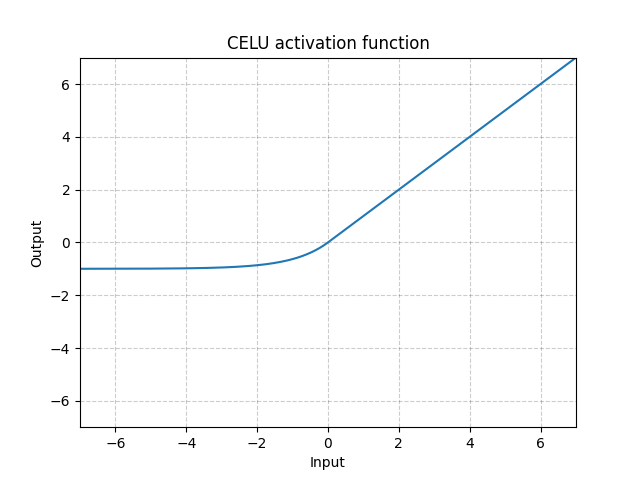
Fig. 7: CELU
SELU - nn.SELU()
\[\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1))\]
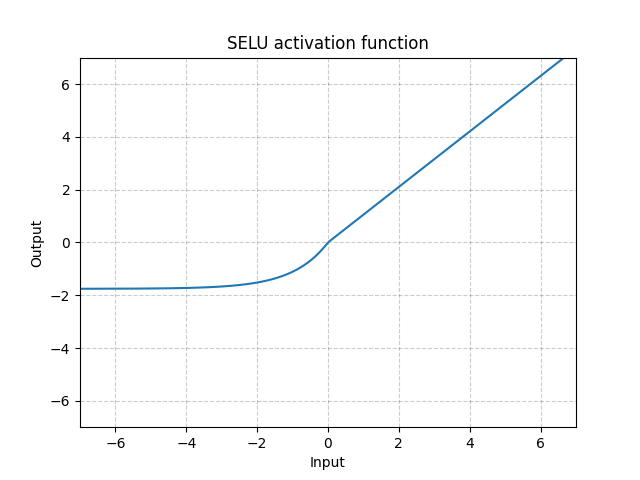
Fig. 8: SELU
GELU - nn.GELU()
\[\text{GELU(x)} = x * \Phi(x)\]
donde $\Phi(x)$ es la Función de Distribución Acumulada para la Distribución Gaussiana.
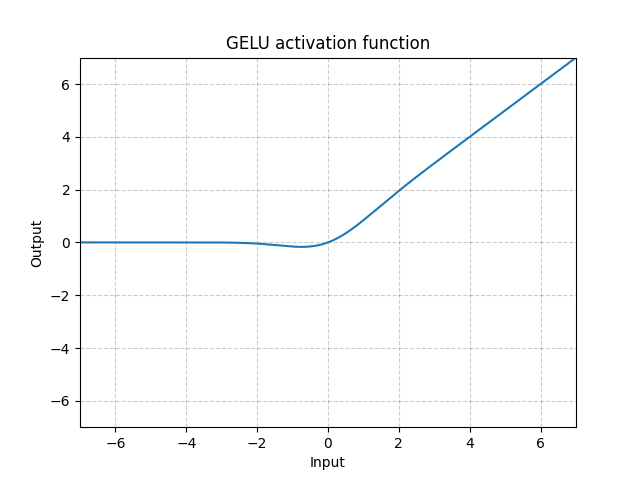
Fig. 9: GELU
ReLU6 - nn.ReLU6()
\[\text{ReLU6}(x) = \min(\max(0,x),6)\]
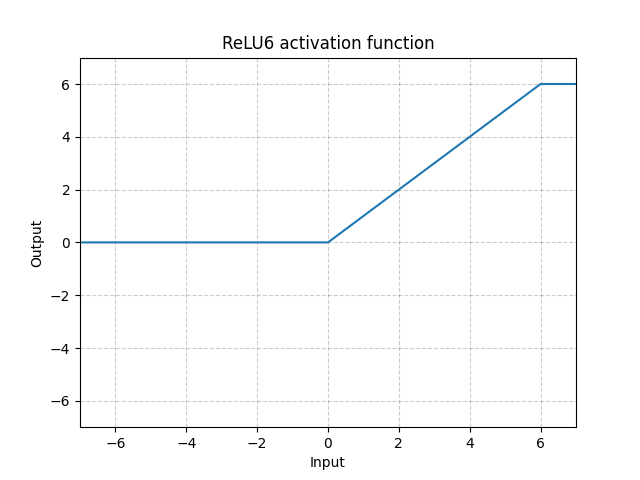
Fig. 10: ReLU6
Esta es la ReLU saturada en 6. Pero no hay ninguna razón en particular por la que escoger 6 como valor de saturación, así que podemos hacerlo mejor utilizando la función Sigmoide como abajo.
Sigmoide - nn.Sigmoid()
\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}\]
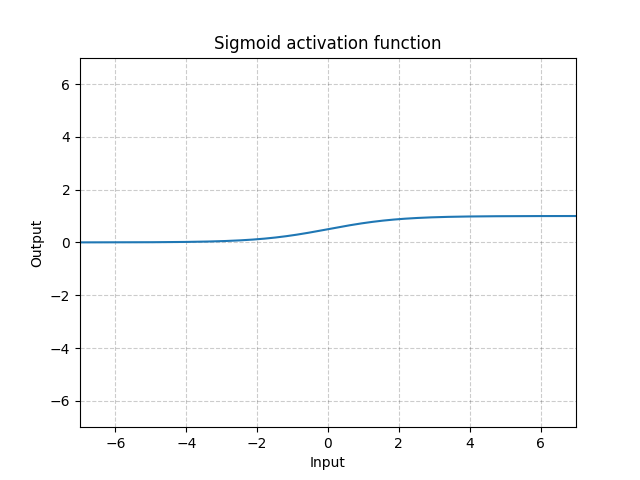
Fig. 11: Sigmoide
Si apilamos sigmoides en muchas capas, puede ser ineficiente para el aprendizaje del sistema y requerirá una inicialización cuidadosa. Esto es debido a que si la entrada es muy grande o pequeña, el gradiente de la función sigmoide se acerca a 0. En este caso, no hay un gradiente que fluya hacia atrás para actualizar los parámetros. Esto también se conoce como el problema del gradiente saturado. Por tanto, para las redes neuronales profundas, se prefiere utilizar funciones con un punto no diferenciable (como la ReLU).
Tanh - nn.Tanh()
\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]
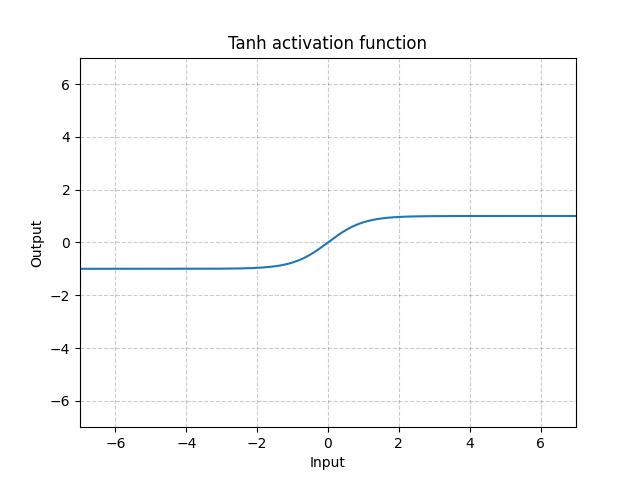
Fig. 12: Tanh
La Tanh es básicamente idéntica a la Sigmoide excepto porque está centrada, con un rango de entre -1 y 1. La salida de la función tendrá una media aproximadamente de 0. Por lo tanto, el modelo convergerá más rápido. Ten en cuenta que usualmente la convergencia será más rápida si el promedio de cada variable de entrada es cercano a cero. Un ejemplo es la Normalización por Lotes (Batch Normalization en inglés).
Softsign - nn.Softsign()
\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]
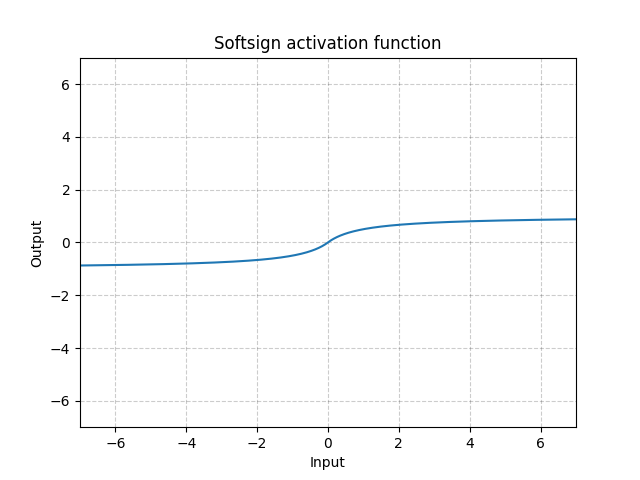
Fig. 13: Softsign
Es similar a la función Sigmoide pero se acerca lentamente a la asíntota y hasta cierto punto resuelve el problema del desvanecimiento del gradiente.
Tanh dura - nn.Hardtanh()
\[\text{Tanh dura}(x) = \begin{cases}
1, & \text{si} x > 1\\
-1, & \text{si} x < -1\\
x, & \text{en otro caso}
\end{cases}\]
El rango de la región lineal [-1, 1] puede ser ajustado usando min_val y max_val.
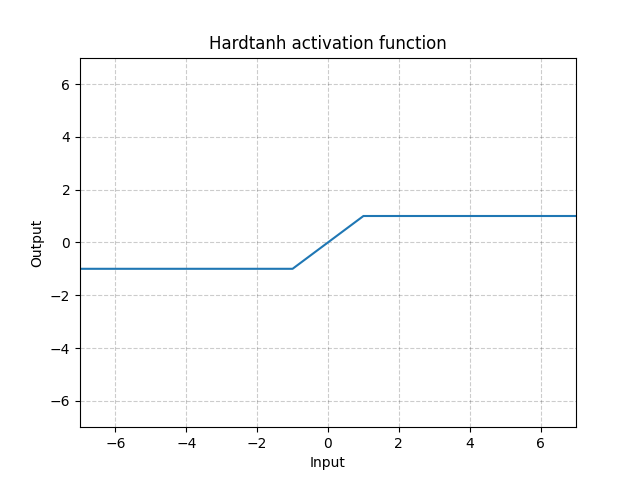
Fig. 14: Hardtanh
Funciona sorprendentemente bien, en especial cuando los pesos se mantienen dentro del pequeño rango de valores.
Umbral - nn.Threshold()
\[y = \begin{cases}
x, & \text{si} x > \text{umbral}\\
v, & \text{en otro caso}
\end{cases}\]
Se usa muy raramente puesto que no se puede propagar el gradiente hacia atrás. Es también lo que evitaba que se usara la propagación hacia atrás en los 60s y 70s cuando se utilizaban neuronas binarias.
Tanh encogida - nn.Tanhshrink()
\[\text{Tanh encogida}(x) = x - \tanh(x)\]
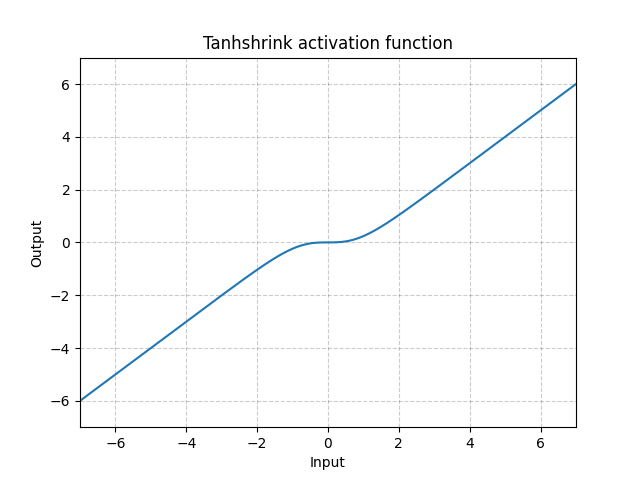
Fig. 15: Tanh encogida
Se usa muy raramente, con la excepción de la codificación dispersa, donde se usa para computar el valor de la variable latente.
Encogimiento suave - nn.Softshrink()
\[\text{Encogimiento suave}(x) = \begin{cases}
x - \lambda, & \text{si} x > \lambda\\
x + \lambda, & \text{si} x < -\lambda\\
0, & \text{en otro caso}
\end{cases}\]
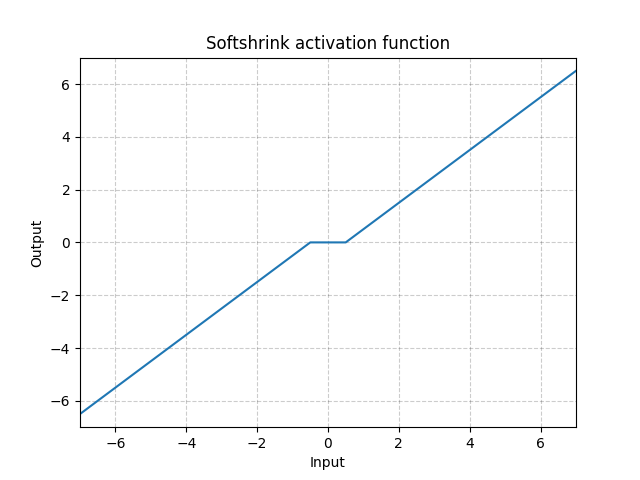
Fig. 14: Encogimiento suave
Esta función básicamente encoge la variable por un valor constante hacía 0, y la obliga a ser 0 si el valor de la variable es cercano a 0. Puedes pensar en ella como un paso del gradiente para los criterios $\ell_1%. Es también uno de los pasos del Algoritmo de Encogimiento-Umbralización Iterativo (ISTA, por sus siglas en inglés). Pero no se usa a menudo en las redes neuronales estándar como función de activación.
Encogimiento duro- nn.Hardshrink()
\[\text{EncogimientoDuro}(x) = \begin{cases}
x, & \text{si} x > \lambda\\
x, & \text{si} x < -\lambda\\
0, & \text{en otro caso}
\end{cases}\]
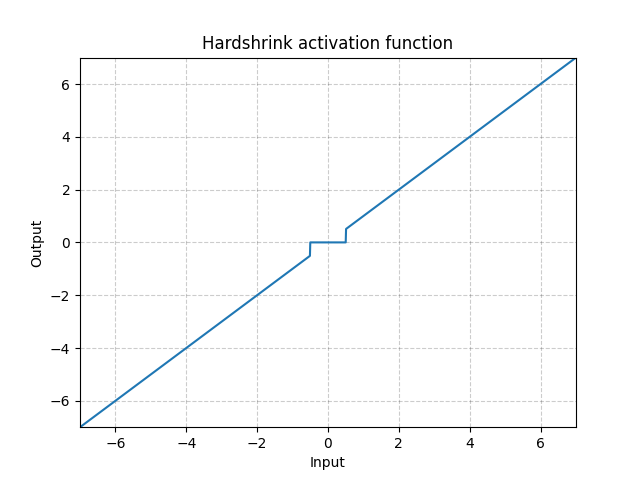
Fig. 17: Encogimiento duro
Se usa muy raramente, con la excepción de la codificación dispersa.
LogSigmoide - nn.LogSigmoid()
\[\text{LogSigmoide}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right)\]
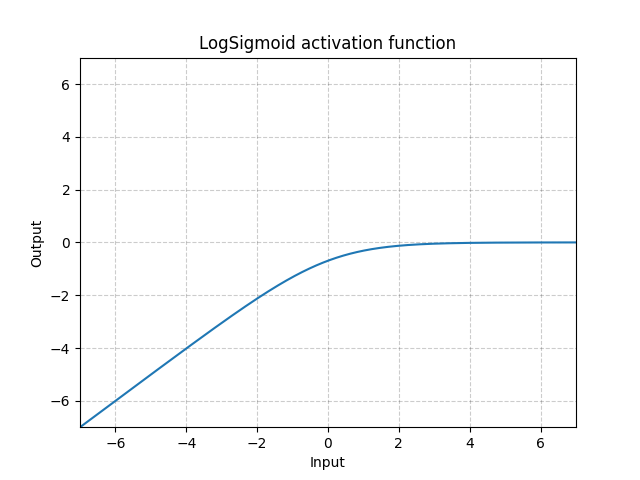
Fig. 18: LogSigmoide
Se usa mayormente en la función de costo pero no es común en las activaciones.
Softmin - nn.Softmin()
\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)}\]
Convierte números en una distribución de probabilidad.
Soft(arg)max - nn.Softmax()
\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]
LogSoft(arg)max - nn.LogSoftmax()
\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right)\]
Se usa mayormente en la función de costo pero no es común en las activaciones.
Q&A funciones de activación
preguntas respecto a la nn.PReLU()
- ¿Por qué querríamos el mismo valor de $a$ para todos los canales?
Diferentes canales pueden tener distintos valores de $a$. Podrías usar $a$ como un parámetro de todas las unidades. También podría ser compartida como un mapa de características.
- ¿Aprendemos $a$? ¿Es ventajoso aprender $a$?
Puedes aprender $a$ o mantenerlo como un valor fijo. La razón para mantenerlo fijo es asegurar que la no-linealidad te de un gradiente distinto de 0 incluso si está en una región negativa. Hacer $a$ un parámetro que se pueda aprender permite que el sistema convierta la no-linealidad ya sea en un mapeo lineal o en una rectificación completa. Podría ser util para algunas aplicaciones como implementar un detector de bordes sin importar la polaridad de los bordes.
- ¿Qué tan compleja quieres que sea tu no-linealidad?
En teoría, podemos parametrizar una función no-lineal completa de formas muy complicadas, ya sea con parámetros de resorte, polinomios de Chebyshev, etc. Parametrizar la función podría ser parte del proceso de aprendizaje.
- ¿Cuál es la ventaja de parametrizar en comparación con tener más unidades en tu sistema?
En realidad depende de lo que quieras hacer. Por ejemplo, cuando haces regresión en un espacio de baja dimensionalidad, la parametrización podría ayudar. Sin embargo, si tu tarea está en un espacio de alta dimensionalidad tal como el reconocimiento de imágenes, es necesario tener solo «una» no-linealidad y la no-linealidad monotónica funcionará mejor. En resumen, puedes parametrizar cualquier función que desees pero no te dará una ventaja tan grande.
Preguntas respecto a los puntos no diferenciables
- Un punto no diferenciable versus dos puntos no diferenciables
Double kink is a built-in scale in it. Esto significa que si la capa de entrada se multiplica por dos (o si la amplitud de la señal se multiplica por dos), entonces las salidas serán completamente distintas. La señal tendrá una no-linealidad mayor, y por tanto tendrás un comportamiento completamente distinto de la salida. Mientras que, si tienes una función con solo un punto no diferenciable, si multiplicas la salida por dos, entonces tu salida también será multiplicada por dos.
- Diferencias entre una activación no-lineal con puntos no diferenciables y una activación no-lineal suave. ¿Por qué/cuando es preferible alguna de ellas?
Es un asunto de equivarianza de escala. Si tienes un punto no diferenciable duro, al multiplicar la entrada por dos, la salida se multiplica por dos. Si tienes una transición suave, por ejemplo, al multiplicar la entrada por 100, la salida luce como si tuvieras un punto no diferenciable duro ya que la parte suave se encoge por un factor de 100. Si divides la entrada por 100, el punto no diferenciable se convierte en una función convexa muy suave. Así, al cambiar la escala de la entrada, cambias el comportamiento de la unidad de activación.
Algunas veces esto podría ser un problema. Por ejemplo, cuando entrenas una red neuronal multicapa y tienes dos capas que están una detrás de la otra. No tienes un buen control respecto a qué tan grandes son los pesos de una capa en relación con los pesos de la otra capa. Si tienes una no-linealidad a la que le importan las escalas, tu red no tiene elección respecto a qué tamaños de la matriz de pesos pueden usarse en la primera capa puesto que esto cambiará completamente su comportamiento.
Una forma de arreglar este problema es colocar un escalado duro en los pesos de cada capa para que se puedan normalizar dichos pesos, como por ejemplo la normalización por lotes. Así, la varianza de los valores que entran en cada unidad se mantiene constante. Si se mantiene fija la escala, entonces el sistema no tiene ninguna forma de escoger qué parte de la no-linearidad usar en funciones con dos puntos no diferenciables. Esto se podría volver un problema si la parte «fija» se vuelve muy «lineal». Por ejemplo, la Sigmoide se vuelve casi lineal cerca del cero, y por tanto las salidas de la normalización por lotes (cercanas a 0) no se pueden activar de forma «no-lineal».
No es completamente claro el por qué las redes profundas funcionan mejor con funciones con un solo punto no diferenciable. Probablemente se deba a la propiedad de equivarianza de escala.
El coeficiente de temperatura en una función soft(arg)max.
- ¿Cuándo usamos el coeficiente de temperatura y por qué lo usamos?
Hasta cierto punto, la temperatura es redundante con los pesos que entran. Si tienes sumas ponderadas entrando a tu función softmax, el parámetro $\beta$ es redundante con el tamaño de los pesos.
La temperatura controla qué tan dura será la distribución de la salida. Cuando $\beta$ es muy grande, se vuelve muy cercana a uno o a zero. Cuando $\beta$ es pequeño, es más suave. Cuando el límite de $\beta$ es igual a cero, se comporta como un promedio. Cuando $\beta$ tiende a infinito, se comporta como argmax. Deja de ser su versión suave. Entonces, si tienes algún tipo de normalización antes de la softmax, ajustar este parámetro te permite controlar la dureza. A veces, puedes empezar con un $\beta$ pequeño para que puedas tener descensos de gradiente con buen comportamiento y, a menuda que se hace la ejecución, si quieres unas decisiones más duras en tu mecanismo de atención, incrementas $\beta$. Así, puedes hacer decisiones más séveras. Este truco se conoce como enfriamiento. Puede ser útil para mezclas de expertos como un mecanismo de auto-atención.
Funciones de costo
PyTorch también tiene muchas funciones de costo implementadas. Revisaremos algunas de ellas.
nn.MSELoss()
Esta función devuelve el error cuadrático medio (norma L2 al cuadrado) entre cada elemento de la entrada $x$ y el objetivo $y$. También se conoce como función de costo L2.
Si estamos usando un mini-lote de $n$ muestras, entonces hay $n$ costos, uno para cada muestra en el lote. Podemos decirle a la función de costo que mantenga ese costo como un vector o que lo reduzca.
Si no se reduce (es decir, se coloca reduction='none”), el costo es
donde $N$ es el tamaño del lote, $x$ y $y$ son tensores de formas arbitrarias con un total de n elementos cada uno.
Las opciones de reducción están debajo (recuerda que el valor por defecto es reduction='mean').
La operación de suma opera sobre todos los elementos y divide por $n$.
La división por $n$ se puede evitar si se coloca reduction = 'sum'.
nn.L1Loss()
Esta función mide el error absoluto medio (MAE, por sus siglas en inglés) entre cada elemento de la entrada $x$ y el objetivo $y$ (o la salida obtenida y la salida deseada).
Si no se reduce (es decir, se coloca reduction='none”), el costo es
donde $N$ es el tamaño del lote, $x$ y $y$ son tensores de formas arbitrarias con un total de n elementos cada uno.
También tiene las opciones de reduction 'mean' y 'sum' similar a las que tiene nn.MSELoss().
Caso de uso: La función de costo L1 es más robusta contra valores atípicos y ruido en comparación con la función de costo L2. En la L2, los errores de los puntos atípicos o ruidosos se elevan al cuadrado, así que la función de costo se vuelve muy sensible a dichos puntos.
Problem: La función de costo L1 no es diferenciable al fondo (0). Tenemos que tener cuidado al manejar sus gradientes (es decir, Encogimiento suave). Esto motiva la siguiente función de costo L1 suave:
nn.L1Loss()
Esta función usa la función de costo L2 si el error absoluto por elemento está por debajo de 1 y la L1 en caso contrario.
\(\text{costo}(x, y) = \frac{1}{n} \sum_i z_i\) , donde $z_i$ está dado por
\[z_i = \begin{cases}0.5(x_i-y_i)^2, \quad &\text{si } |x_i - y_i| < 1\\ |x_i - y_i| - 0.5, \quad &\text{en otro caso} \end{cases}\]También tiene opciones de reduction.
Esto es promovido por Ross Girshick (Fast R-CNN). La función de costo L1 suave es también conocida como la función de costo Huber o la Red Elástica cuando se usa como función objetivo.
Caso de uso: Es menos sensible a valores atípicos que la MSELoss y es suave al fondo. Esta función a menudo se usa en visión por computador para resguardarse de valores atípicos.
Problema: La función tiene una escala ($0.5$ en la función de arriba).
L1 vs. L2 para Visión por Computador
Al hacer predicción cuando tenemos muchos $y$’s diferentes:
- Si usamos el MSE (función de costo L2), resulta en un promedio de todos los $y$, lo que en Visión por Computador significa que tendremos una imagen borrosa.
- Si usamos la función de costo L1, el valor de $y$ que minimiza la distancia L1 es el medio, que no es borroso, pero recuerda que el medio es difícil de definir en múltiples dimensiones.
Usar la L1 resulta en imágenes más nítidas al predecir.
nn.NLLLoss()
La función de costo de log-verosimilitud negativa es la que se usa en problemas de clasificación con C clases.
Es importante resaltar que, matemáticamente, la entrada de la NLLLoss deberían ser log-verosimilitudes, pero PyTorch no verifica eso. Así que el efecto es hacer que el componente deseado sea tan grande como sea posible.
La función de costo sin reducir (es decir, con el :attr:reduction puesto en 'none”) se puede describir así:
, donde $N$ es el tamaño de lote.
Si reduction no es 'none' (por defecto es 'mean'), entonces
Esta función de costo tiene un argumento opcional weight que puede ser enviado usando un Tensor en 1D en el que se le asigna un peso a cada una de las clases. Esto es útil cuando se trabaja con un conjunto de entrenamiento desbalanceado.
Pesos y Clases Desbalanceadas:
El vector de pesos es útil si la frecuencia es diferente para cada categoría/clase. Por ejemplo, la frecuencia de la gripe común es mucho más alta que la del cáncer de pulmón. Entonces podemos simplemente incrementar el peso para las categorías que tienen un pequeño número de muestras.
Sin embargo, en vez de poner un peso, es mejor ecualizar la frecuencia durante el entrenamiento para que podamos aprovechar mejor los gradientes estocásticos.
Para ecualizar las clases en el entrenamiento, ponemos muestras de cada clase en un buffer distinto. Entonces generamos cada mini-lote escogiendo el mismo número de muestras de cada buffer. Cuando el buffer pequeño se queda sin muestras, volvemos a iterar recorriéndolo desde el principio de nuevo hasta que se usen todas las muestras de la clase más grande. Esto nos da una frecuencia igual para todas las categorías al recorrer estos buffers circulares. Nunca deberíamos ir a la fácil ecualizando la frecuencia al no usar todas las muestras de la clase mayoritaria. ¡No dejes datos en el piso!
Un problema obvio del método mencionado arriba es que nuestro modelo de red neuronal no conocería la frecuencia relativa real de las muestras. Para resolver esto, afinamos el sistema corriendo unas cuantas épocas al final con la frecuencia de clases real, para que el sistema se adapte a los sesgos en su capa de salida y favorezca cosas que son más frecuentes.
Para imaginar como funciona este esquema, volvamos al ejemplo de las clases de medicina: los estudiantes gastan tanto tiempo en enfermedades raras como en las frecuentse (o incluso más, pues las enfermedades raras a menudo son las más complejas). Ellos aprenden a adaptarse a las características de toda las enfermedades y entonces se corrigen para saber cuales son raras.
nn.CrossEntropyLoss()
Esta función combina nn.LogSoftmax y nn.LLLoss en una sola clase. La combinación de las dos hace que el puntaje de la clase correcta sea tan grande como sea posible.
La razón por la que las dos funciones se combinan es por la estabilidad numérica del cómputo del gradiente. Cuando el valor que sale de la softmax es muy cercano a 1 o 0, el logarítmo de dicho valor puede estar muy cerca de 0 o de $-infty$. La pendiente del logarítmo cerca de 0 tiende a $\infty$, lo que causa que el paso intermedio en la propagación hacía atrás tenga problemas numéricos. Cuando se combinan ambas funciones, se satura el gradiente y se obtiene un número razonable al final.
La entrada esperada es el puntaje sin normalizar para cada clase.
Esta función de costo se puede describir como:
\[\text{loss}(x, c) = -\log\left(\frac{\exp(x[c])}{\sum_j \exp(x[j])}\right) = -x[c] + \log\left(\sum_j \exp(x[j])\right)\]o en caso de que se especifique el argumento weight:
Los costos se promedían entre todas las observaciones para cada mini-lote.
Una interpretación física de la función de costo de entropía cruzada se relaciona con la divergencia Kullback–Leibler (divergencia KL), donde se mide la divergencia entre las dos distribuciones. Aquí, las (quasi) distribuciones se representan por el vector x (predicciones) y la distribución objetivo (un vector one-hot con 0 en las clases equivocadas y 1 en la clase correcta).
Matemáticamente,
\[H(p,q) = H(p) + \mathcal{D}_{KL} (p \mid\mid q)\]donde \(H(p,q) = - \sum_i p(x_i) \log (q(x_i))\) es la entropía-cruzada (entre dos distribuciones), \(H(p) = - \sum_i p(x_i) \log (p(x_i))\) es la entropía, y \(\mathcal{D}_{KL} (p \mid\mid q) = \sum_i p(x_i) \log \frac{p(x_i)}{q(x_i)}\) es la divergencia KL.
nn.AdaptiveLogSoftmaxWithLoss()
Esta es una aproximación eficiente de la función softmax para grandes cantidades de clases (por ejemplo, millones de clases) Esta función implementa trucos para mejorar la velocidad de cómputo.
Los detalles del método se describen en Efficient softmax approximation for GPUs por Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, Hervé Jégou.
📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Alberto Mario Ceballos-Arroyo
13 Apr 2020