El *Truck Backer-Upper*

Planteamiento

El objetivo de esta tarea es construir un controlador que aprende por sí mismo (self-learning controller) que controle la dirección de un camión mientras retrocede hacia una plataforma de carga desde cualquier posición y orientación inicial arbitraria.

Fig. 1: El camión, tráiler y plataforma de carga

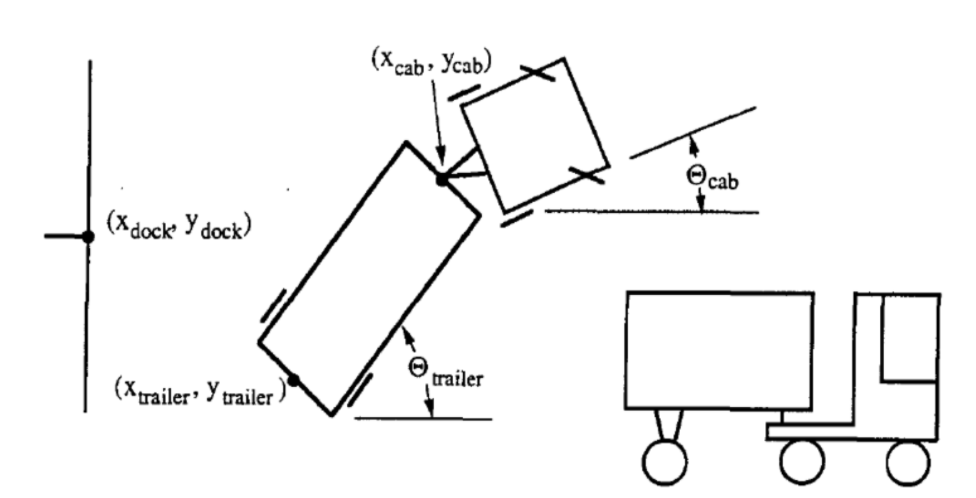El estado del camión está representado por seis parámetros:

• $tcab$: Ángulo del camión
• $\xcab, \ycab$: La coordenada cartesiana del acoplamiento (o parte frontal del tráiler)
• $\ttrailer$: Ángulo del tráiler
• $\xtrailer, \ytrailer$: La coordenada cartesiana del (parte trasera del) tráiler

La meta del controlador es seleccionar un ángulo apropiado $\phi$ en cada instante $k$, en el que el camión retrocederá en una pequeña distancia fija. El éxito se mide con dos criterios:

1. La parte trasera del tráiler está en posición paralela a la pared de la plataforma de carga, es decir, $\ttrailer = 0$.
2. La parte trasera del tráiler ($\xtrailer, \ytrailer$) está tan cerca como sea posible al punto ($x_{dock}, y_{dock}$) como se muestra anteriormente.

Más parámetros y visualización

|| |

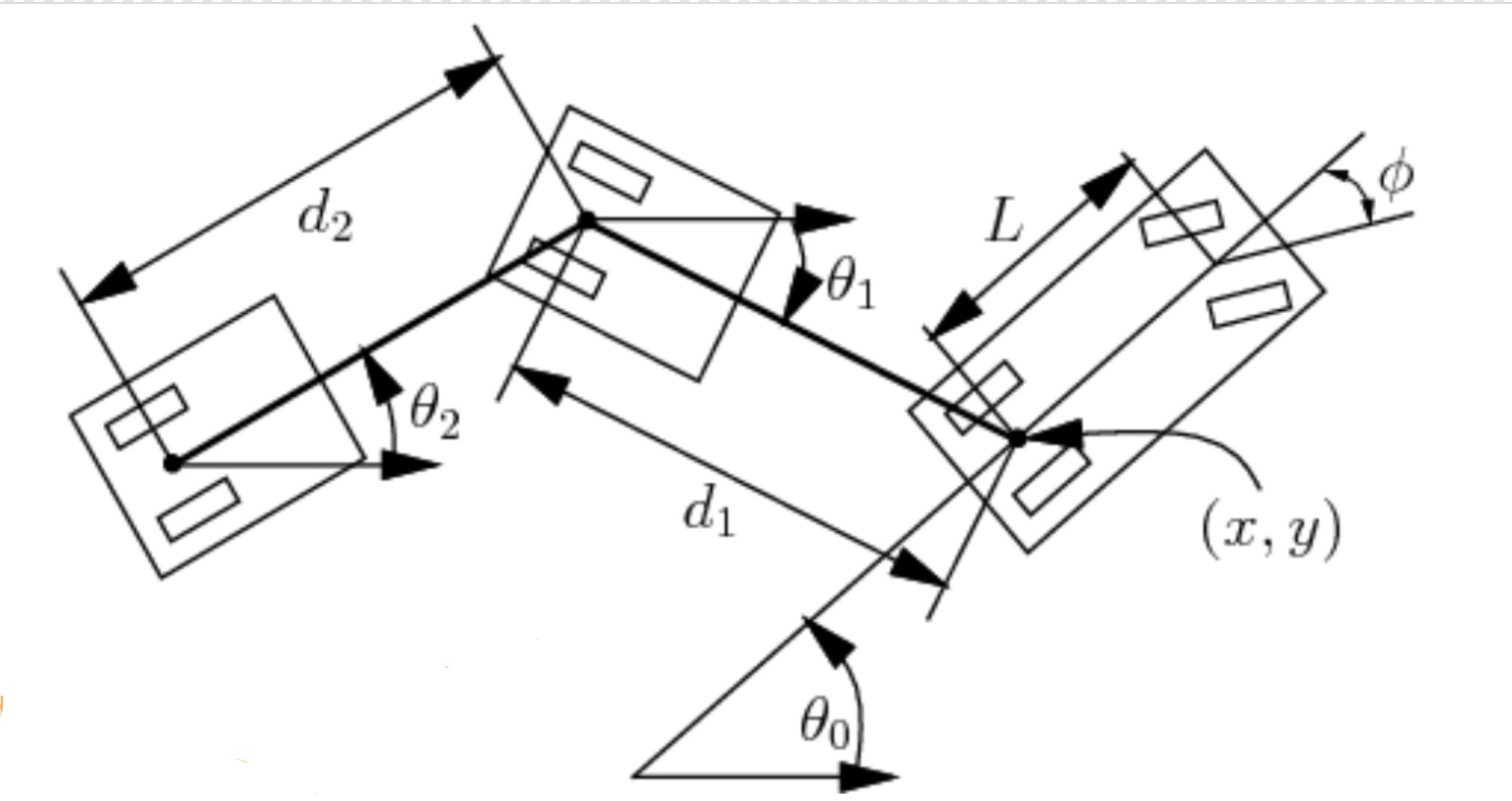
En esta sección, también consideramos unos cuantos parámetros más que se muestran en la figura 2. Dados la longitud $L$ del camión; la distancia $d_1$ entre el camión y el tráiler; la longitud $d_2$ del tráiler, etc., podemos calcular al cambio del ángulo y las posiciones:

Aquí, $s$ denota la rapidez con signo y $\phi$, el ángulo negativo de dirección. Ahora podemos representar el estado con solo cuatro parámetros: $\xcab$, $\ycab$, $\theta_0$ y $\theta_1$. Esto es porque los parámetros de longitud son conocidos y $\xtrailer, \ytrailer$ están determinados por $\xcab, \ycab, d_1, \theta_1$.

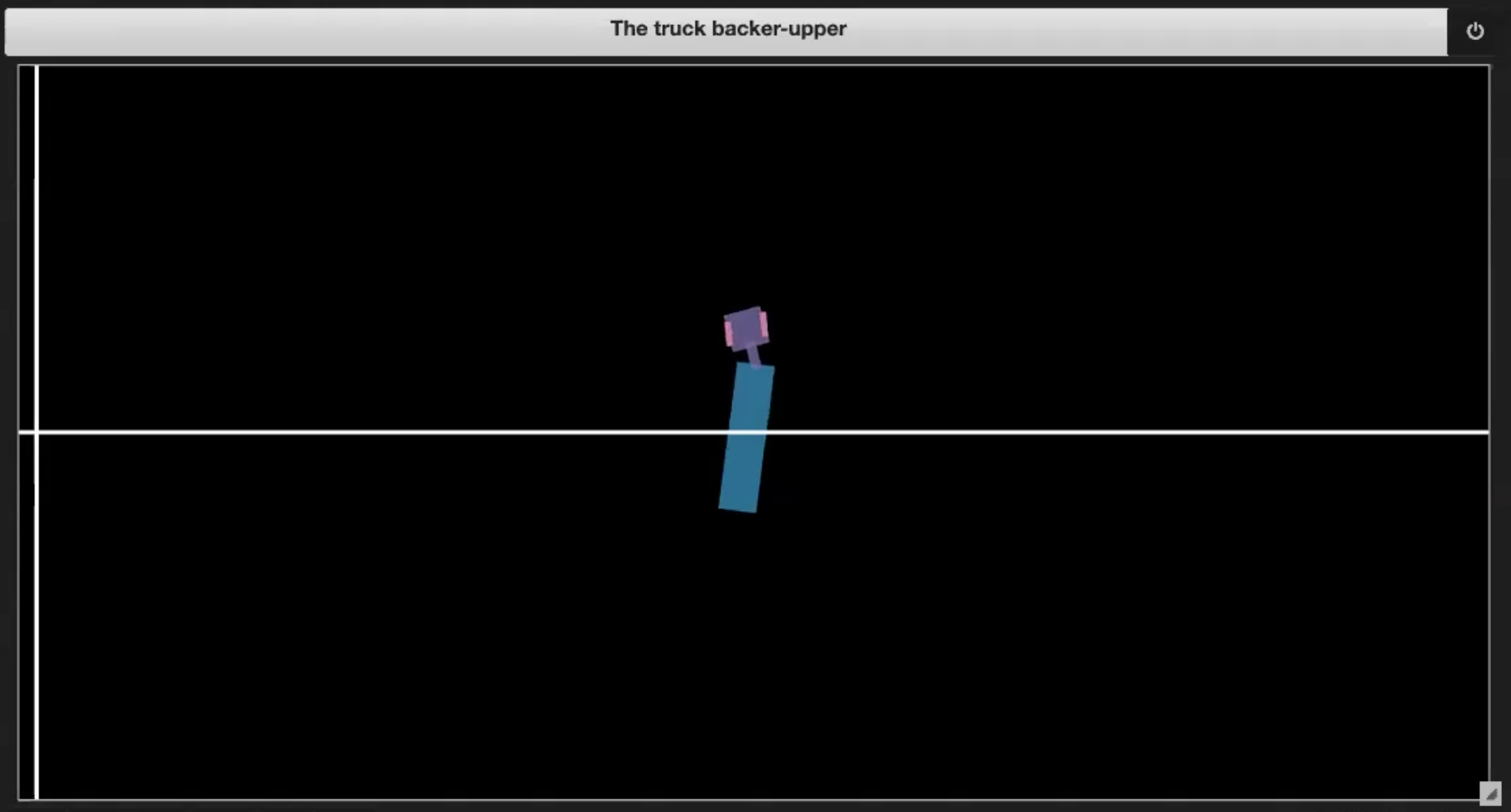
En el Jupyter Notebook del repositorio de Aprendizaje Profundo, tenemos algunos ambientes de ejemplo mostrados en las figuras 3 (de la 1 a la 4):

Fig. 3.1: Imagen de muestra del ambiente	Fig. 3.2: Conduciendo hacia sí mismo (efecto tijera)
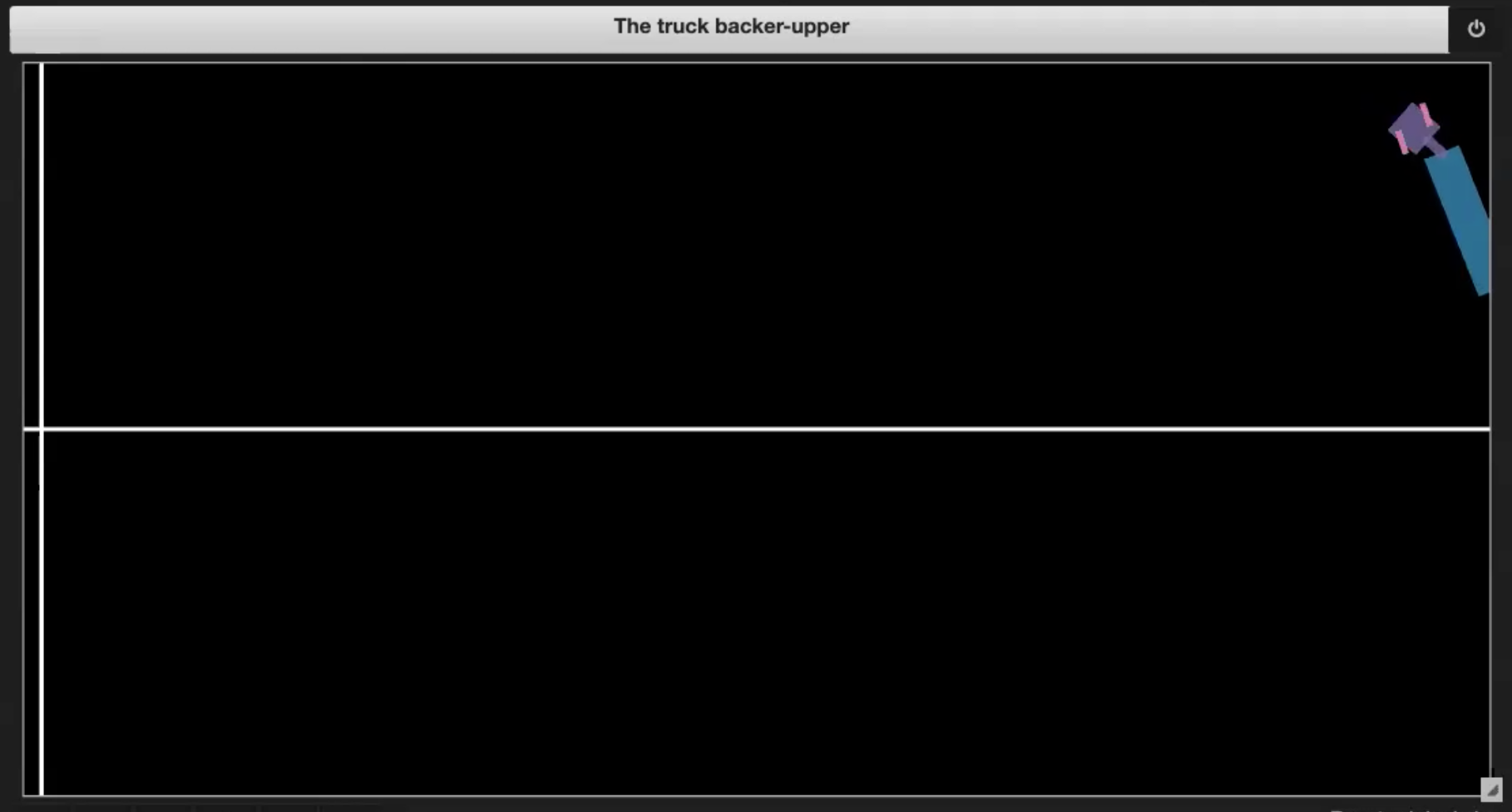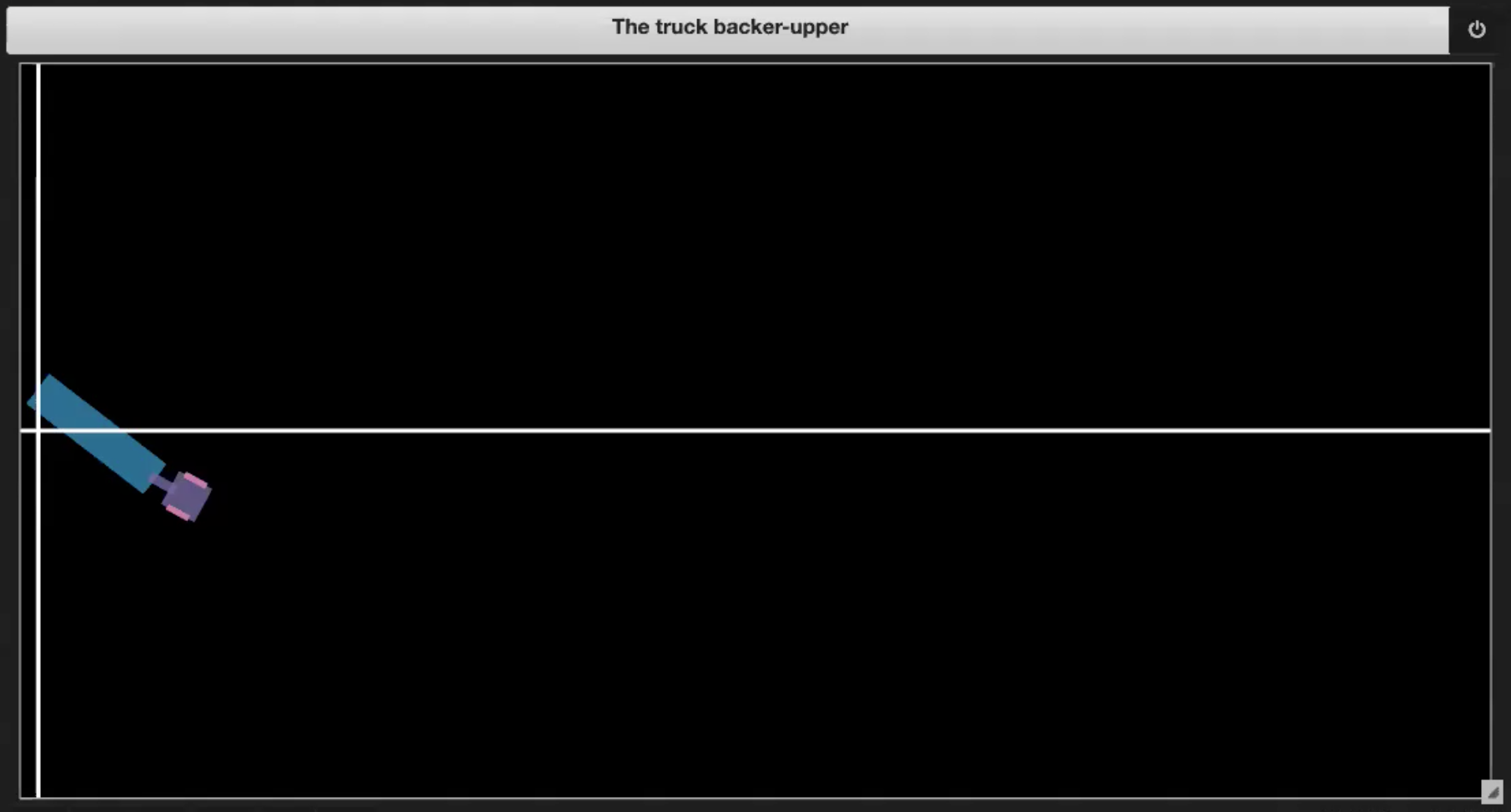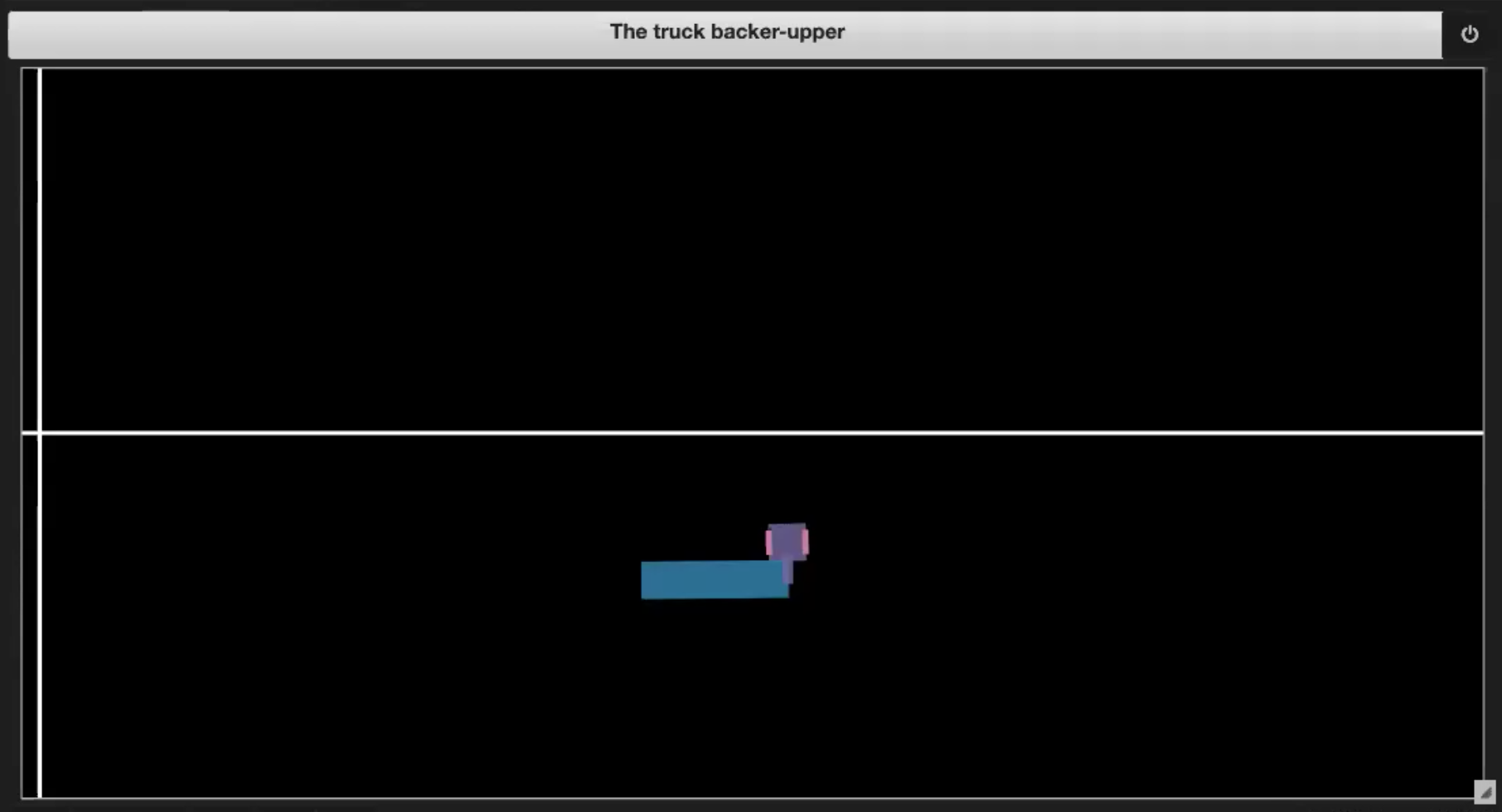
Fig. 3.3: Saliéndose de los límites	Fig. 3.4: Llegando a la plataforma

En cada incremento de tiempo $k$, una señal de dirección que va desde $-\frac{\pi}{4}$ a $\frac{\pi}{4}$ se alimentará y el camión retrocederá usando el ángulo correspondiente.

Hay varias situaciones en las que la secuencia puede terminar:

• Si el camión conduce hacia sí mismo (efecto tijera, como en la figura 3.2)
• Si el camión sale de los límites (mostrado en la figura 3.3)
• Si el camión llega a la plataforma (mostrado en la figura 3.4)

Entrenamiento

El proceso de entremiento comprende dos etapas: (1) el entrenamiento de una red neuronal para que sea un emulador de la cinemática del camión y el tráiler y (2) el entrenamiento de un controlador en red neuronal para controlar el camión.

Fig. 4: Diagrama general

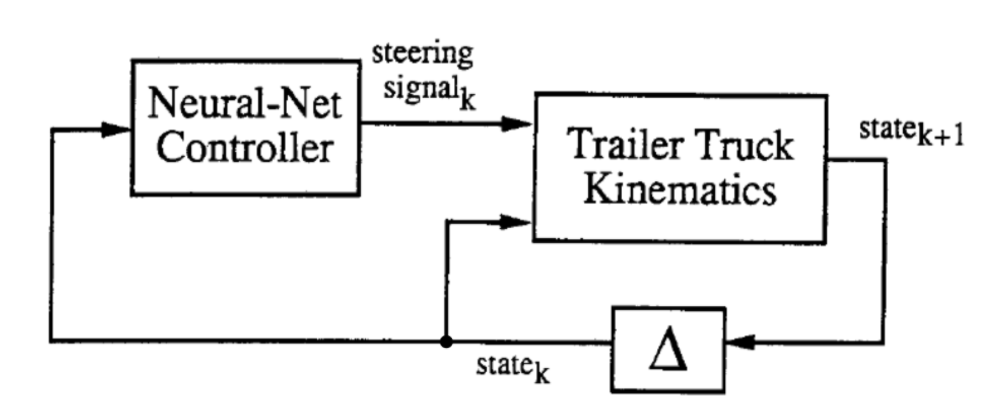Como se muestra anteriormente, en el diagrama abstracto, los dos bloques son las dos redes neuronales que se entrenarán. En cada incremento de tiempo $k$, la cinemática del tráiler y el camión (Trailer Truck Kinematics en la figura 4), o lo que hemos estado llamando el emulador, toma como entrada el vector de estado de seis dimensiones y la señal de dirección generada por el controlador y genera un nuevo vector de estado de seis dimensiones en el tiempo $k + 1$.

Emulador

El emulador toma como entrada la ubicación actual ($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$) más la dirección $\phi^t$ y su salida es el estado en el siguiente incremento de tiempo ($\tcab^{t+1}$,$\xcab^{t+1}, \ycab^{t+1}$, $\ttrailer^{t+1}$, $\xtrailer^{t+1}$, $\ytrailer^{t+1}$). Consiste en una capa oculta lineal, con una función de activación ReLU y una capa de salida lineal. Usamos MSE (error cuadrático medio) como función de costo y entrenamos el emulador por medio de descenso de gradiente estocástico.

|| |

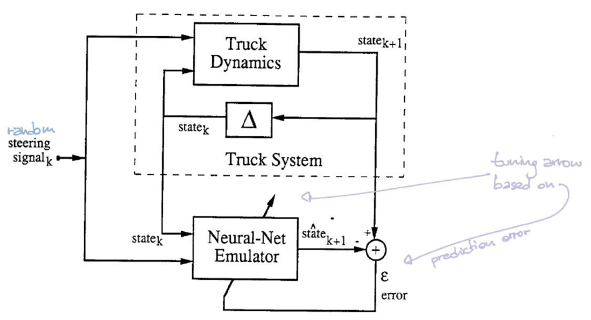En esta configuración, el simulador puede decirnos la ubicación del siguiente incremento dada la ubicación actual y el ángulo de dirección. Por lo tanto, en realidad no necesitamos una red neuronal que emule el simulador. Sin embargo, en un sistema más complejo, puede que no tengamos acceso a las ecuaciones subyacentes del sistema, es decir, no tenemos las leyes del Universo en una bonita forma computable. Puede que solo observemos datos que registren secuencias de las señales de dirección y sus trayectorias correspondientes. En este caso, queremos entrenar una red neuronal para emular la dinámica de este sistema complejo.

Para entrenar el emulador, hay dos funciones importantes en Class truck a las que necesitamos echar un vistazo cuando entrenamos el emulador.

La primera es la función step que da el estado de salida del camión después del cálculo.

def step(self, ϕ=0, dt=1):

    # Revisa si hay condiciones ilegales
    if self.is_jackknifed():
        print('The truck is jackknifed!')
        return

    if self.is_offscreen():
        print('The car or trailer is off screen')
        return

    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()

    # Realiza la actualización del estado
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

La segunda es la función state que da el estado actual del camión.

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

Generamos primero dos listas. Generamos una lista de entrada al agregar el ángulo de dirección ϕ generado aleatoriamente y el estado inicial que viene del camión al correr truck.state(). Y generamos una lista de salida que se forma con el estado de salida del camión que puede calcularse con truck.step(ϕ).

Ahora podemos entrenar el emulador:

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)

    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)

    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()

    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

Presta atención a que torch.randperm(len(train_inputs)) nos da una permutación aleatoria de los índices dentro del intervalo desde $0$ hasta la longitud de las entradas de entrenamiento menos $1$. Después de la permutación de los índices, se elige ϕ_state en cada instante de la lista de entrada en el índice i. Ingresamos ϕ_state a través de la función del emulador que tiene una capa de salida lineal y obtenemos next_state_prediction (la predicción del siguiente estado). Fíjate que el emulador es una red neuronal definida como sigue:

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

Aquí usamos MSE (error cuadrático medio) para calcular la pérdida entre el siguiente estado verdadero y el siguiente estado predicho, en donde el siguiente estado verdadero viene de la lista de salida con el índice i que corresponde con el índice del estado ϕ_state de la lista de entrada.

Controlador

En la figura 5, el bloque $\matr{C}$ representa el controlador. Toma como entrada el estado actual y tiene como salida un ángulo de dirección. Posteriormente, el bloque $\matr{T}$ (emulador) toma el estado y el ángulo para producir el siguiente estado.

Fig. 5: Diagrama de flujo de la transición de estado

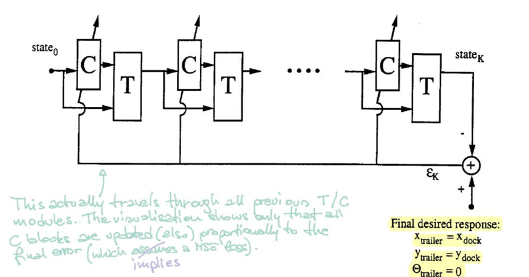Para entrenar el controlador, empezamos desde un estado inicial aleatorio y repetimos el procedimiento ($\matr{C}$ y $\matr{T}$) hasta que el tráiler está en posición paralela a la plataforma. El error se calcula al comparar la ubicación del tráiler y la ubicación de la plataforma. Posteriormente, encontramos los gradientes usando retropropagación y actualizamos los parámetros del controlador por medio de SGD (descenso de gradiente estocástico).

Estructura detallada del modelo

Este es un grafo detallado del proceso ($\matr{C}$, $\matr{T}$). Comenzamos con un estado (vector de seis dimensiones), lo multiplicamos por una matriz de pesos ajustables y obtenemos 25 unidades ocultas. Después, lo pasamos a través de otro vector de pesos ajustables para obtener la salida (señal de dirección–steering signal–). De manera similar, ingresamos el estado y el ángulo $\phi$ (vector de siete dimensiones) a través de dos capas para producir el estado del siguiente incremento de tiempo.

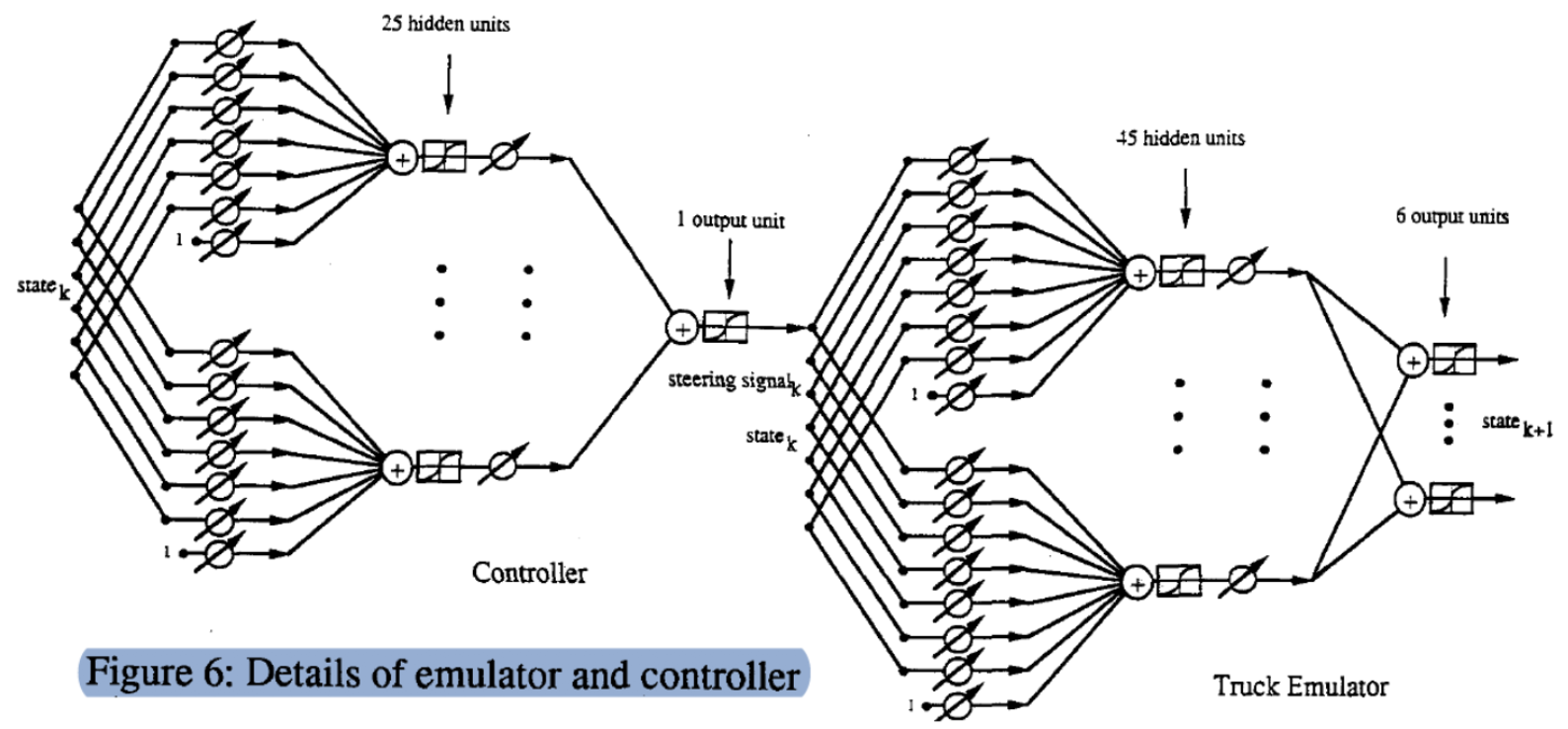
Para ver esto más claramente, mostramos la implementación exacta del emulador:

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

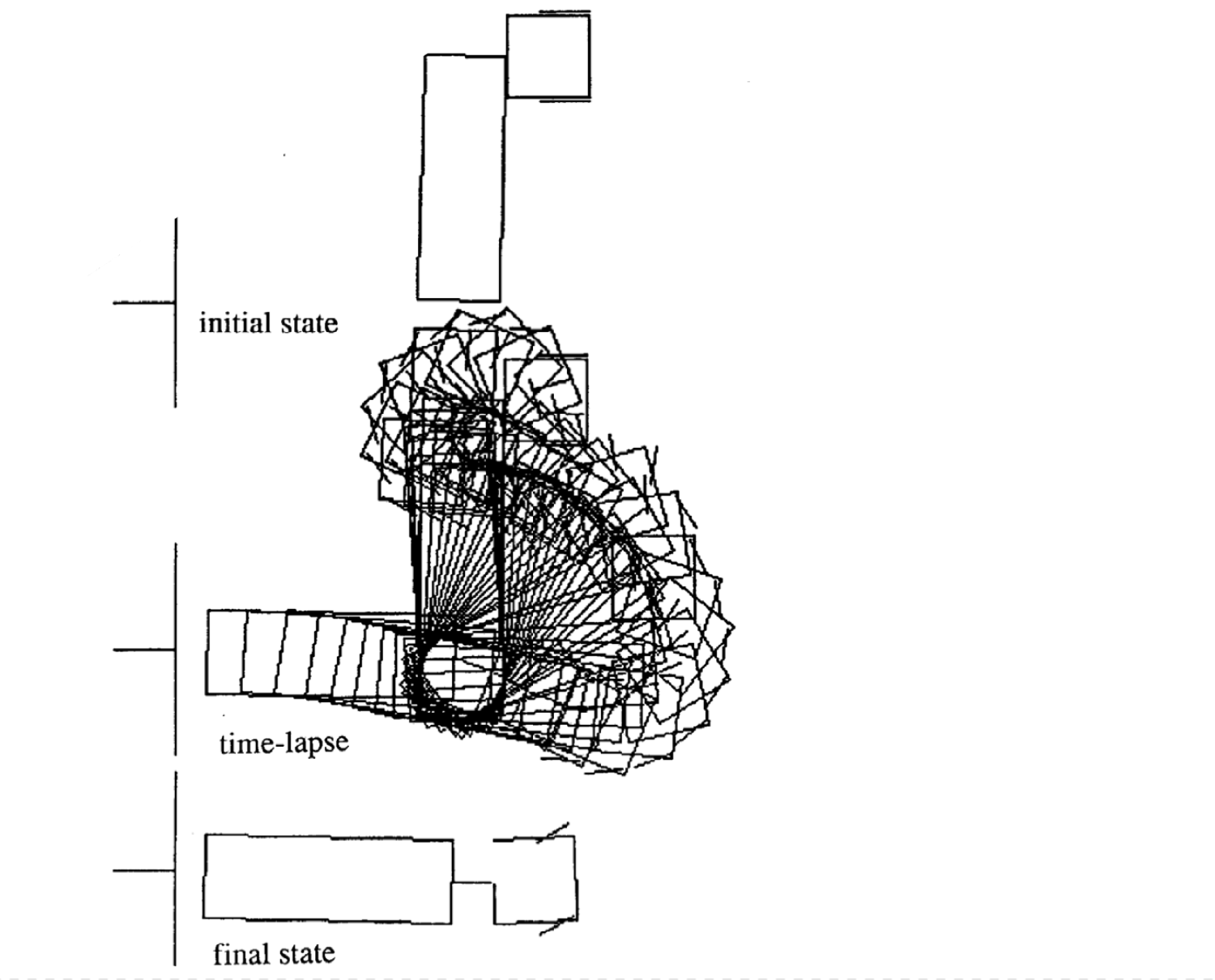
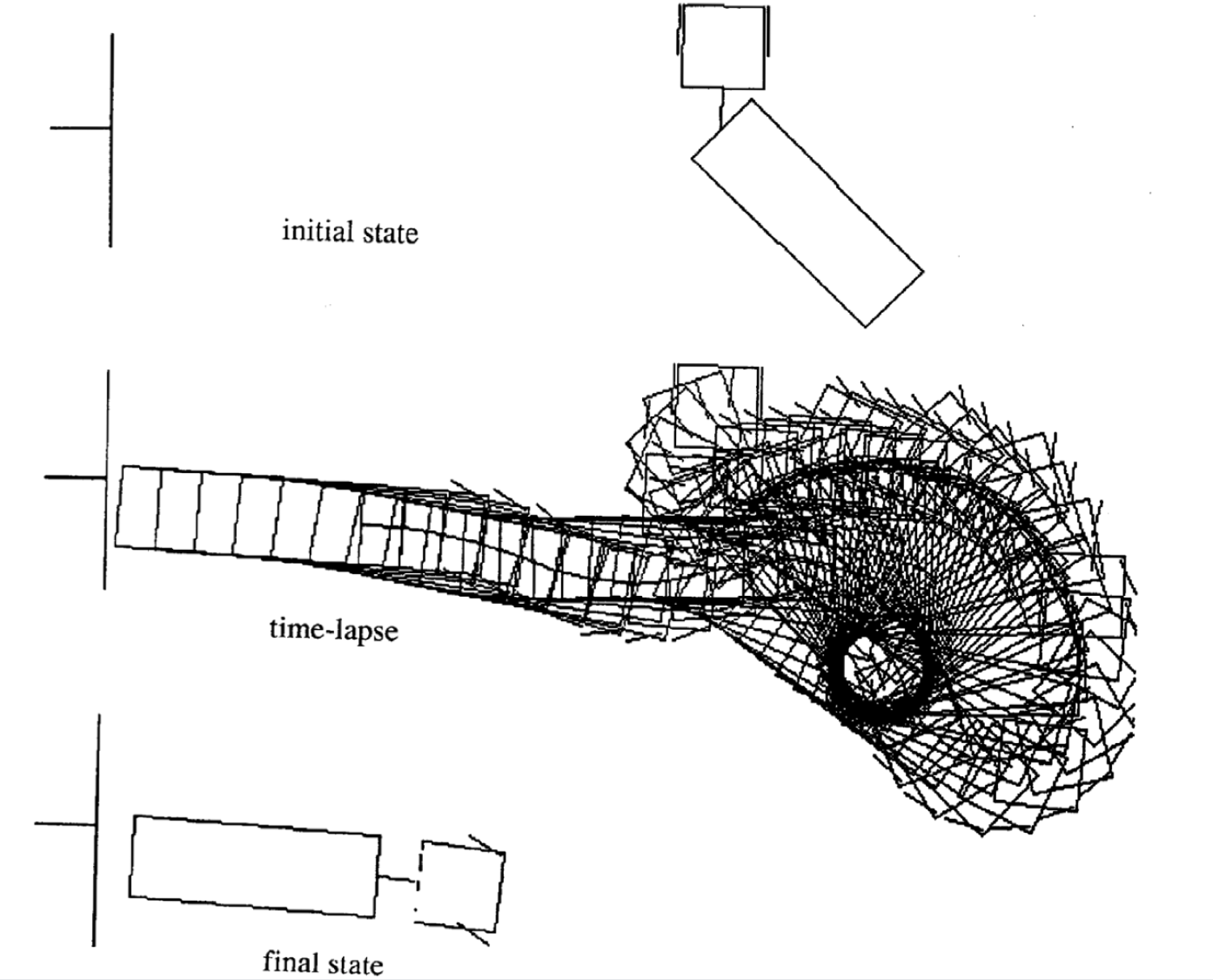
Ejemplos de movimiento

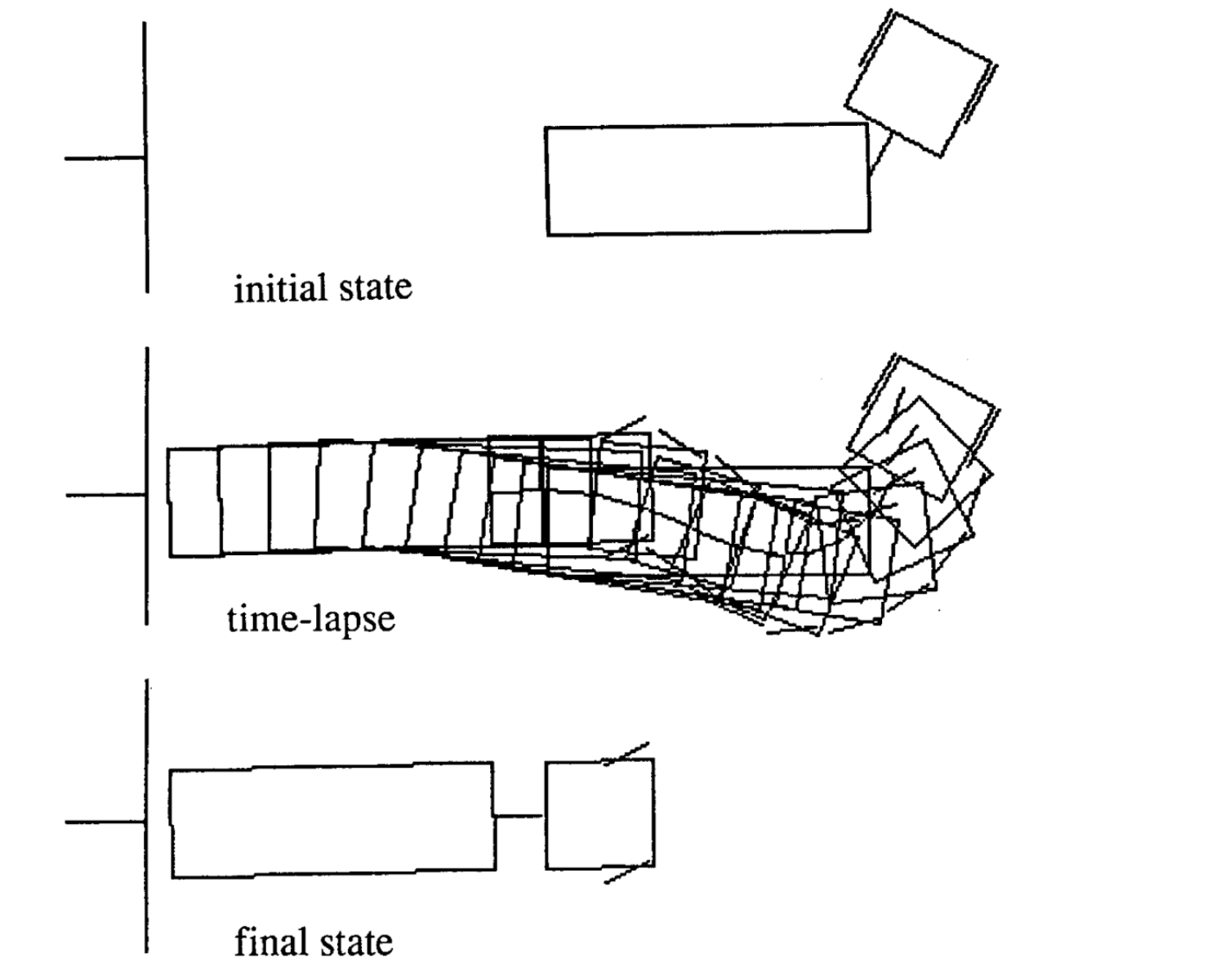
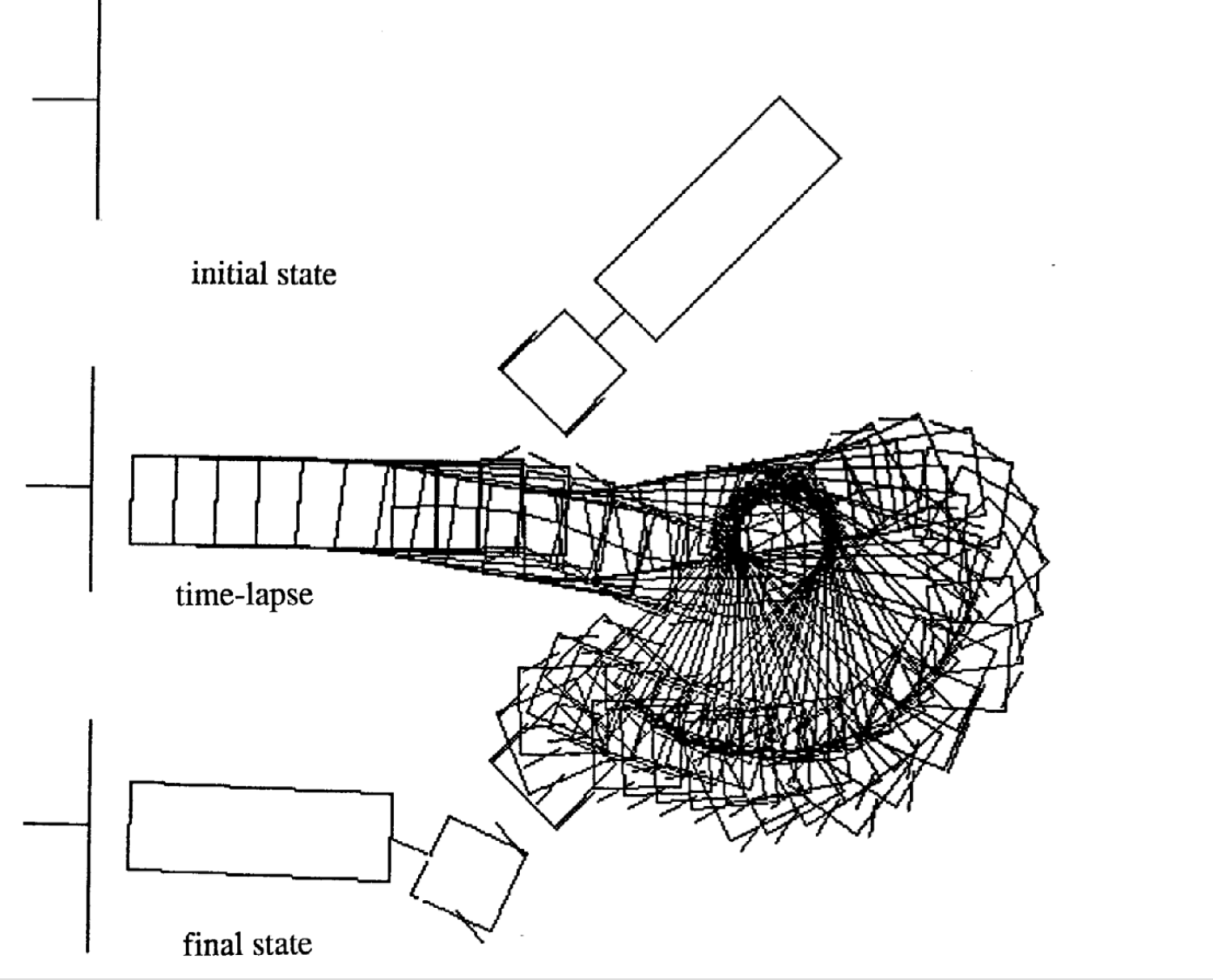
A continuación hay cuatro ejemplos de movimiento para diferentes estados inciales. Fíjate que el número de incrementos de tiempo en cada episodio varía.

Recursos adicionales:

Puedes encontrar un demo completamente funcional en: https://tifu.github.io/truck_backer_upper/. También revisa el código; el cual puede encontrarse en: https://github.com/Tifu/truck_backer_upper.