Aprendizaje auto-supervisado - ClusterFit y ARPI

###¿Qué falta en las tareas de “pretexto”? La esperanza de la generalización

La tarea de pretexto generalmente comprende pasos de preentrenamiento que se auto-supervisan y luego tenemos nuestras tareas de transferencia que a menudo son de clasificación o detección. Esperamos que la tarea de preentrenamiento y las tareas de transferencia estén “alineadas”, es decir, resolver la tarea de pretexto ayudará a resolver las tareas de transferencia muy bien. Por lo tanto, se investiga mucho en el diseño de una tarea pretexto e implementarla muy bien.

Sin embargo, no está muy claro por qué la realización de una tarea no semántica debe producir buenas características… Por ejemplo, ¿por qué deberíamos esperar aprender sobre “semántica” mientras resolvemos algo como un rompecabezas? ¿O por qué se espera que “predecir hashtags” a partir de imágenes ayude a aprender un clasificador en tareas de transferencia? Por lo tanto, la pregunta sigue siendo: ¿Cómo deberíamos diseñar buenas tareas de pre-entrenamiento que estén bien alineadas con las tareas de transferencia?

Una forma de evaluar este problema es mirando las representaciones en cada capa (ver Fig. 1). Si las representaciones de la última capa no están bien alineadas con la tarea de transferencia, entonces la tarea de preentrenamiento puede no ser la tarea correcta a resolver.

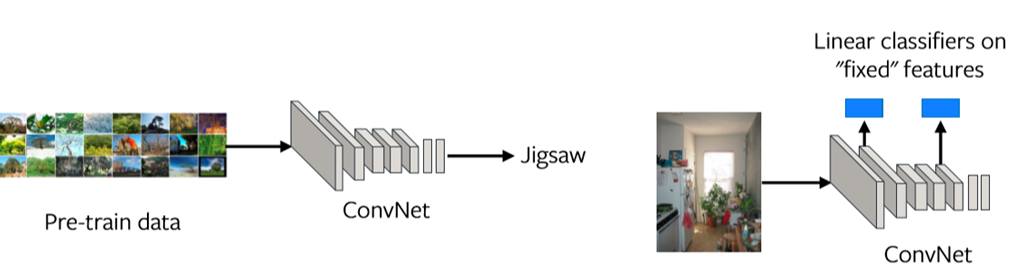
Fig. 1: Las representaciones de las características en cada capa

La Fig. 2 muestra la Media de Precisión Promedio en cada capa para los Clasificadores Lineales en el VOC07 usando el Preentrenamiento del Rompecabezas. Está claro que la última capa es muy especializada para el problema del rompecabezas.

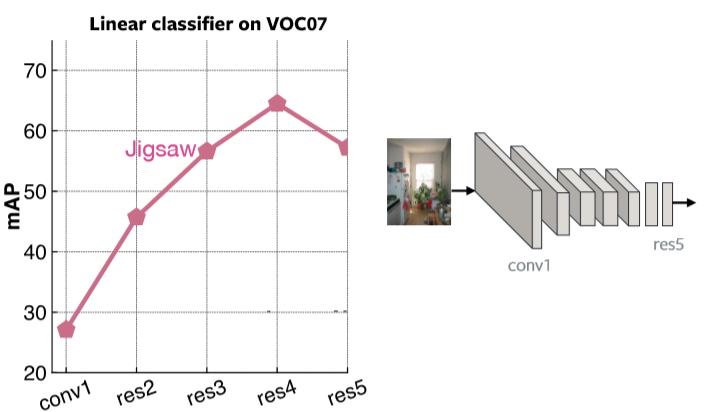
Fig. 2: Desempeño del rompecabezas basado en cada capa

###¿Qué queremos de las características pre-entrenadas?

• Representar cómo se relacionan las imágenes unas con otras

• ClusterFit: Mejorar la generalización de las representaciones visuales

• Ser robusto a los “factores de perturbación” – Invariancia

P.ej. la ubicación exacta de los objetos, la iluminación, el color exacto

• ARIP: Aprendizaje auto-supervisado de Representaciones Invariantes de Pretexto

Dos formas de lograr las propiedades anteriores son Agrupamiento y Aprendizaje Constrastivo. Estos métodos han comenzado a desempeñarse mucho mejor que las tareas de pretexto que se diseñaron hasta ahora. Un método que pertenece a la agrupación en clústeres es ClusterFit y otro que cae en invariancia es ARIP.

ClusterFit: Mejorando la generalización de las representaciones visuales

Agrupar el espacio de características es una forma de ver qué imágenes se relacionan entre sí.

Método

ClusterFit sigue dos pasos. Uno es el paso del clúster, y el otro es el paso de la predicción.

Clúster: Agrupamiento de características

Tomamos una red preentrenada y la usamos para extraer un montón de características de un conjunto de imágenes. La red puede ser cualquier tipo de red preentrenada. El agrupamiento de K-medias se realiza entonces sobre estos rasgos, así que cada imagen pertenece a un cluster, que se convierte en su etiqueta.

Fig. 3: Paso del clúster

Ajuste: Predecir la asignación del clúster

Para este paso, entrenamos una red desde cero para predecir las pseudo etiquetas de las imágenes. Estas pseudo etiquetas son las que obtuvimos en el primer paso a través de la agrupamiento.

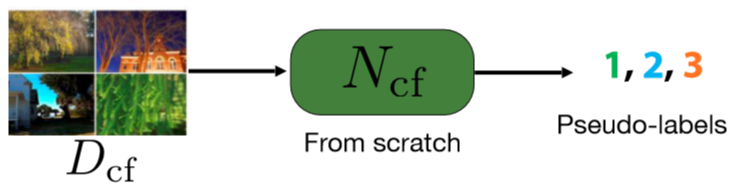
Fig. 4: Paso de Predicción

Una tarea estándar de preentrenamiento y de transferencia primero preentrena una red y luego la evalúa en tareas posteriores, como se muestra en la primera fila de la Fig. 5. ClusterFit aplica el preentrenamiento sobre un conjunto de datos $D_{cf}$ para obtener la red preentrenada $N_{pre}$. Esta red $N_{pre}$ se aplica sobre el conjunto de datos $D_{cf}$ para generar clústeres. Luego aprendemos una nueva red $N_{cf}$ a partir de estos datos. Por último, se usa $N_{cf}$ para todas las tareas posteriores.

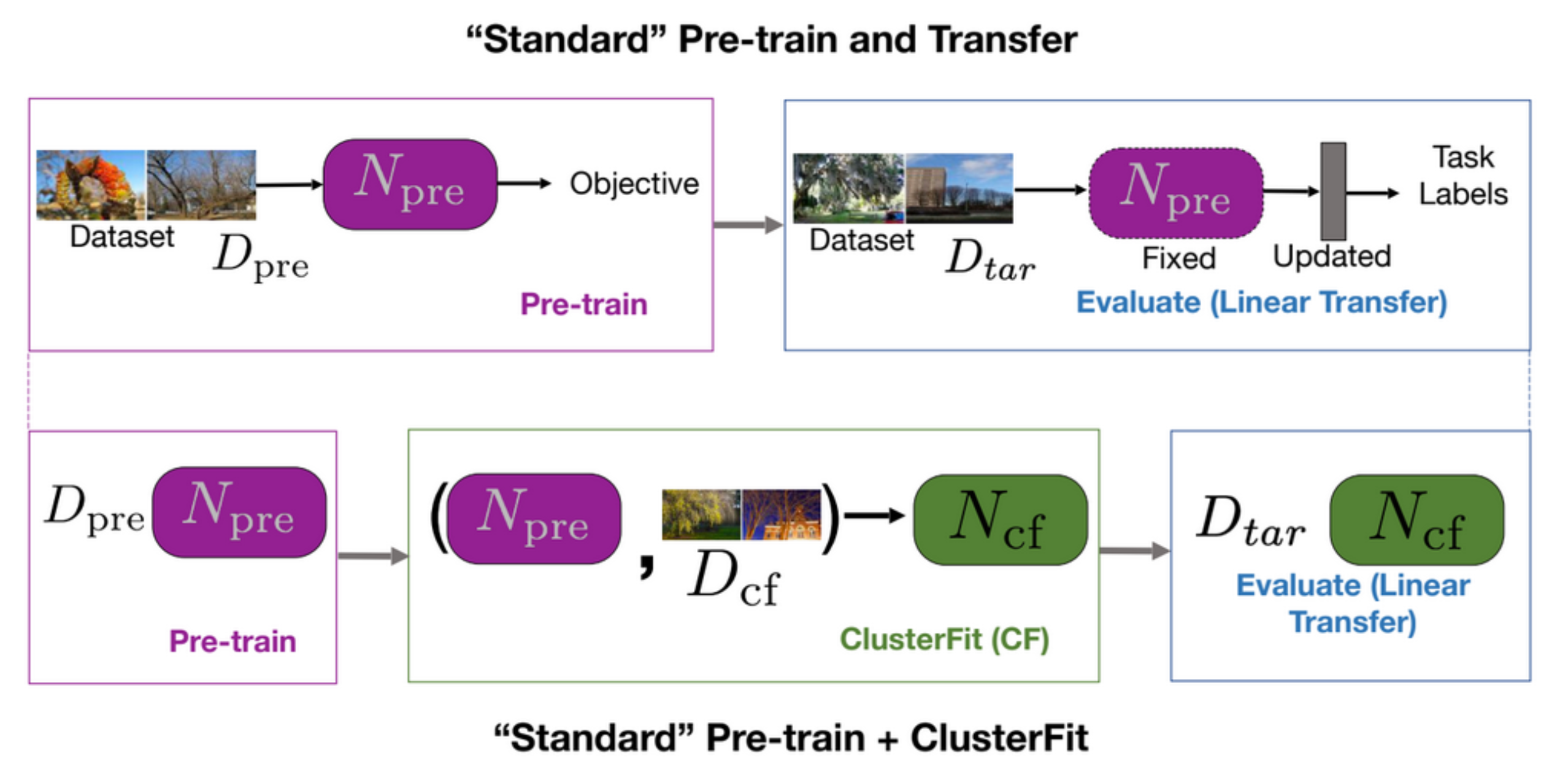
Fig. 5: Preentrenamiento "Estándar" + "Transferencia" *vs.* Preentrenamiento "Estándar" + ClusterFit

¿Por qué ClusterFit funciona?

La razón por la que ClusterFit funciona es que en el paso de agrupación sólo captura la información esencial, y los artefactos se sacan haciendo que la segunda red aprenda algo ligeramente más genérico.

Para entender este punto, se realiza un experimento sencillo. Añadimos ruido de etiqueta a ImageNet-1K, y entrenamos una red basada en este conjunto de datos. Luego, evaluamos la representación de las características de esta red en una tarea posterior en ImageNet-9K. Como se muestra en la Fig. 6, añadimos diferentes cantidades de ruido de etiqueta a ImageNet-1K, y evaluamos el desempeño de la transferencia de diferentes métodos en ImageNet-9K.

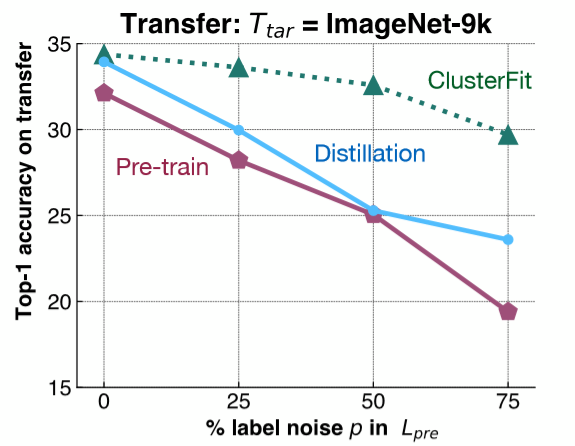
Fig. 6: Experimento de Control

La línea rosada muestra el rendimiento de la red preentrenada, que disminuye a medida que aumenta la cantidad de ruido de la etiqueta. La línea azul representa la destilación del modelo donde tomamos la red inicial y la usamos para generar etiquetas. La destilación generalmente tiene un mejor rendimiento que la red preentrenada. La línea verde, ClusterFit, es consistentemente mejor que cualquiera de estos métodos. Este resultado valida nuestra hipótesis.

• Pregunta: ¿Por qué usar el método de destilación para comparar? ¿Cuál es la diferencia entre la destilación y ClusterFit?

En la destilación del modelo tomamos la red pre-entrenada y usamos las etiquetas que la red predijo de una manera más ligera para generar etiquetas para nuestras imágenes. Por ejemplo, obtenemos una distribución en todas las clases y usamos esta distribución para entrenar la segunda red. La distribución más ligera ayuda a mejorar las clases iniciales que tenemos. En ClusterFit no nos importa el espacio de la etiqueta.

Rendimiento

Aplicamos este método al aprendizaje auto-supervisado. Aquí el rompecabezas se aplica para obtener la red preentrenada $N_{pre}$ en el ClusterFit. En la Fig. 7 vemos que el desempeño de la transferencia en diferentes conjuntos de datos muestra una sorprendente cantidad de ganancias, en comparación con otros métodos auto-supervisados.+

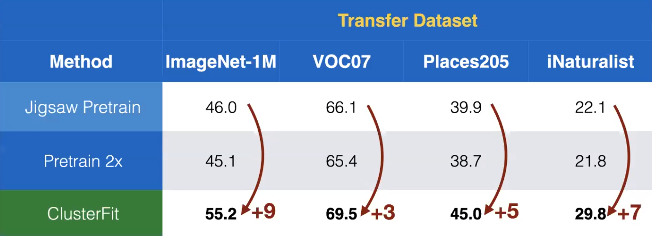
Fig. 7: Rendimiento de transferencia sobre diferentes conjuntos de datos

ClusterFit funciona para cualquier red pre-entrenada. Las ganancias sin datos extra, etiquetas o cambios en la arquitectura pueden verse en la Fig. 8. Así que de alguna manera, podemos pensar en ClusterFit como un paso de afinación auto-supervisado, que mejora la calidad de la representación.

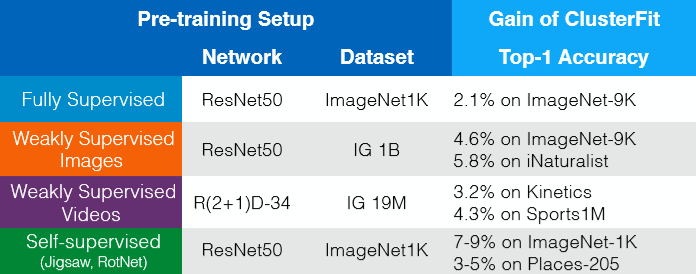
Fig. 8: Ganancias sin datos extra, etiquetas o cambios en la arquitectura

[Aprendizaje auto-supervisado de Representaciones Invariantes de Pretexto (ARIP)]https://www.youtube.com/watch?v=0KeR6i1_56g&t=4748s)

Aprendizaje Contrastivo

El aprendizaje contrastivo es básicamente un marco general que trata de aprender un espacio de características que puede combinar o juntar puntos que están relacionados y separar puntos que no están relacionados.

Fig. 9: Grupos de Imágenes Relacionadas y No Relacionadas

En este caso, imagina que las cajas azules son los puntos relacionados, los verdes están relacionados y los púrpuras son los puntos relacionados.

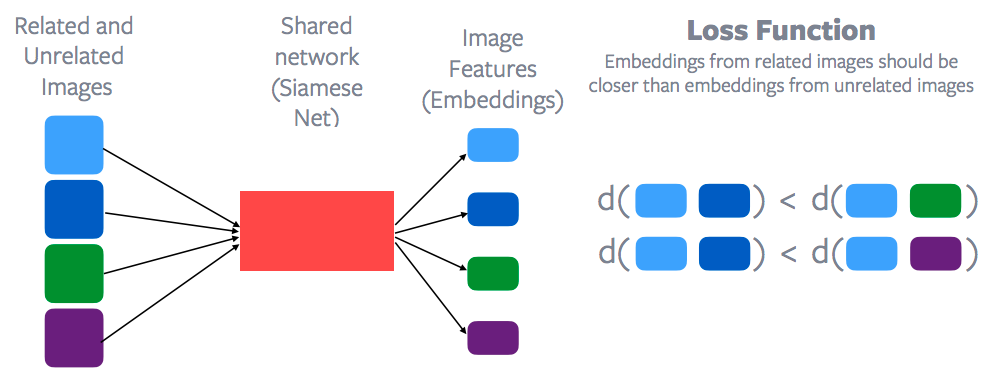
Fig. 10: Aprendizaje Contrastivo y Función de Pérdida

Las características de cada uno de estos puntos de datos se extraerían a través de una red compartida, que se llama Red Siamesa para obtener un montón de características de imagen para cada uno de estos puntos de datos. Luego se aplica una función de pérdida contrastiva para tratar de minimizar la distancia entre los puntos azules en contraposición a, digamos, la distancia entre el punto azul y el punto verde. O la distancia básicamente entre los puntos azules debería ser menor que la distancia entre el punto azul y el punto verde o el punto azul y el punto púrpura. Por lo tanto, el espacio de incrustación de las muestras relacionadas debería estar mucho más cerca que el espacio de incrustación de las muestras no relacionadas. Así que esa es la idea general de lo que es el aprendizaje contrastivo y por supuesto Yann fue uno de los primeros profesores en proponer este método. Así que el aprendizaje contrastivo está haciendo un resurgimiento en el aprendizaje auto-supervisado.

¿Cómo definir lo relacionado o no relacionado?

Y la cuestión principal es cómo definir lo que está relacionado y lo que no lo está. En el caso del aprendizaje supervisado que es bastante claro, todas las imágenes de perros son imágenes relacionadas, y cualquier imagen que no sea un perro es básicamente una imagen no relacionada. Pero no está tan claro cómo definir lo que está relacionado y lo que no lo está en este caso de aprendizaje auto-supervisado. La otra gran diferencia con algo como una tarea de pretexto es que el aprendizaje contrastado realmente razona muchos datos a la vez. Si observas la función de pérdida, siempre implica múltiples imágenes. En la primera fila implica básicamente las imágenes azules y las imágenes verdes y en la segunda fila implica las imágenes azules y las imágenes púrpuras. Pero si miras una tarea como por ejemplo un rompecabezas o una tarea como la rotación, siempre estás razonando sobre una sola imagen de forma independiente. Así que esa es otra diferencia con el aprendizaje contrastivo: razones de aprendizaje contrastivo sobre múltiples puntos de datos a la vez.

Podrían utilizarse técnicas similares a las que se han examinado anteriormente: recuadros de vídeo o la naturaleza secuencial de los datos. Los recuadros que están cerca en un vídeo están relacionados y los recuadros, digamos, de un vídeo diferente o que están más lejos en el tiempo no están relacionados. Y eso ha formado la base de muchos métodos de aprendizaje auto-supervisados en esta área. Este método se llama CPC, que es una codificación predictiva contrastiva, que se basa en la naturaleza secuencial de una señal y básicamente dice que las muestras que están cerca, como en el espacio-tiempo, están relacionadas y las muestras que están más alejadas en el espacio-tiempo no están relacionadas. Una cantidad bastante grande de trabajo explota esto básicamente: puede ser en el dominio del habla, video, texto o imágenes particulares. Y recientemente, también hemos estado trabajando en vídeo y audio, así que básicamente decir que un vídeo y su correspondiente audio son muestras relacionadas y que el vídeo y el audio de un vídeo diferente son básicamente muestras no relacionadas.

Seguimiento de objetos

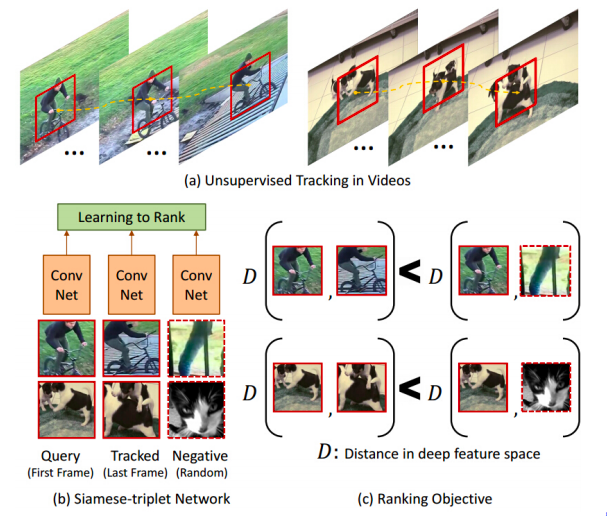
Fig. 11: Siguiendo los Objetos

Algunos de los primeros trabajos, como el aprendizaje auto-supervisado, también utilizan este método de aprendizaje contrastivo y realmente definieron ejemplos relacionados de manera bastante interesante. Si pasas un rastreador de objetos seguidos por un vídeo y eso te da un parche en movimiento, lo que dices es que cualquier parche que haya sido seguido por el rastreador está relacionado con el parche original. En cambio, cualquier parche de un vídeo diferente no es un parche relacionado. Así que eso básicamente da un montón de muestras relacionadas y no relacionadas. En la figura 11(c), tienes esto como una notación de distancia. Lo que esta red intenta aprender es que los parches que provienen del mismo vídeo están relacionados y los parches que provienen de vídeos diferentes no están relacionados. De alguna manera, este aprende automáticamente sobre las diferentes poses de un objeto. Este trata de agruparlos un ciclo, visto desde diferentes ángulos de visión o diferentes poses de un perro.

Parches cercanos vs. parches distantes de una imagen

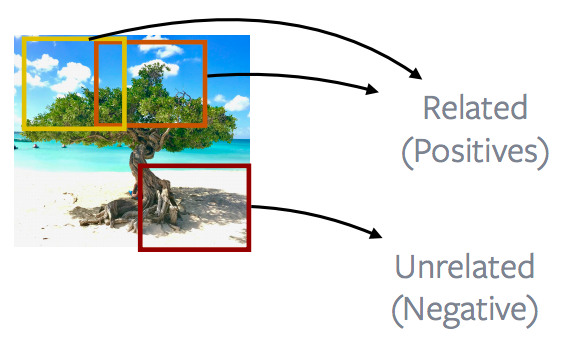
Fig. 12: Parches cercanos *vs.* parches distantes de una imagen

En general, hablando de imágenes, se trabaja mucho en la observación de parches de imágenes cercanas frente a parches distantes, por lo que la mayoría de los métodos CPC v1 y CPC v2 están realmente explotando esta propiedad de las imágenes. Así que los parches de imagen que están cerca se llaman positivos y los parches de imagen que están más alejados se traducen como negativos, y el objetivo es minimizar la pérdida contrastiva usando esta definición de positivos y negativos.

Patches of an image vs. patches of other images

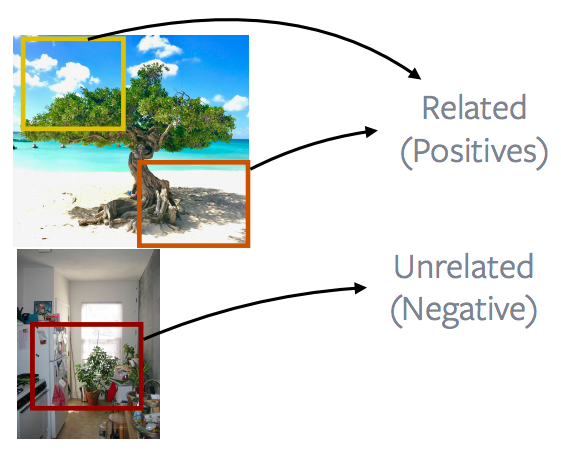
Fig. 13: Parches de una Imagen *vs.* Parches de Otras Imágenes

La forma más popular o de mejor desempeño de hacer esto es mirar los parches que vienen de una imagen y contrastarlos con los parches que vienen de una imagen diferente. Esto forma la base de muchos métodos populares como la discriminación de instancia, MoCo, ARPI(o PIRL por siglas en inglés), SimCLR. La idea es básicamente lo que se está mostrando en la imagen. Para entrar en más detalles, lo que hacen estos métodos es extraer parches completamente aleatorios de una imagen. Estos parches pueden superponerse, pueden llegar a estar contenidos dentro de otro o pueden estar completamente separados y luego aplicar algún aumento de datos. En este caso, digamos, un color intermitente o quitando el color o así sucesivamente. Y entonces estos dos parches se definen como ejemplos positivos. Otro parche se extrae de una imagen diferente. Y este es de nuevo un parche al azar y eso básicamente se convierte en tus negativos. Y muchos de estos métodos extraerán muchos parches negativos y luego básicamente realizarán un aprendizaje contrastivo. Así que hay que relacionar dos muestras positivas, pero hay muchas muestras negativas contra las que hacer aprendizaje contrastivo.

Principio subyacente para las tareas de pretexto

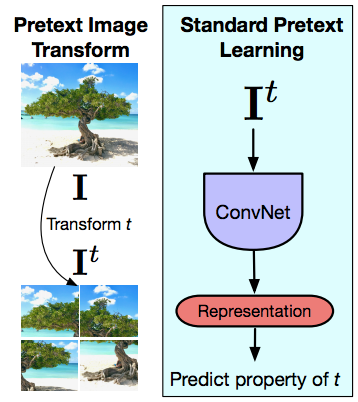
Fig. 14: Transformación de Imágenes de Pretexto y Aprendizaje de Pretexto Estándar

Ahora pasamos a ARPI un poco, y eso es tratar de entender cuál es la principal diferencia de las tareas de pretexto y cómo el aprendizaje contrastivo es muy diferente de las tareas de pretexto. De nuevo, las tareas con pretexto siempre razonan sobre una sola imagen a la vez. Así que la idea es que dándole a una imagen su y previa transformación a esa imagen, en este caso una transformación de rompecabezas, y luego introduciendo esta imagen transformada en una ConvNet e intentando predecir la propiedad de la transformación que aplicaste, la permutación que aplicaste o la rotación que aplicaste o el tipo de color que removiste y así sucesivamente. Así que las tareas de pretexto siempre razonan sobre una sola imagen. Y la segunda cosa es que la tarea que estás realizando en este caso realmente tiene que capturar alguna propiedad de la transformación. Así que realmente tiene que capturar la permutación exacta que se aplican o el tipo de rotación que se aplican, lo que significa que las representaciones de la última capa van a ir mucho ARPI como la transformación de los cambios y eso es por diseño, porque realmente estás tratando de resolver las tareas de pretexto. Pero desafortunadamente, lo que esto significa es que las representaciones de la última capa capturan una propiedad de muy bajo nivel de la señal. Estas capturan cosas como la rotación o algo así. Mientras que lo que se diseña o lo que se espera de estas representaciones es que sean invarintes a estas cosas que debería ser capaz de reconocer un gato, no importa si el gato está en posición vertical o que el gato esté, digamos, inclinado como 90 grados. Mientras que cuando estás resolviendo esa tarea de pretexto particular se impone exactamente lo contrario. Estamos diciendo que deberíamos ser capaces de reconocer si esta imagen está en posición vertical o si esta imagen está básicamente girada hacia los lados. Hay muchas excepciones en las que realmente quieres que estas representaciones de bajo nivel sean covariantes y muchas de ellas tienen que ver con las tareas que estás realizando y bastantes tareas en 3D realmente quieren ser predictivas. Así que quieres predecir qué transformaciones de cámara tienes: estás viendo dos vistas del mismo objeto o algo así. Pero a menos que tengas ese tipo de aplicación específica para muchas tareas semánticas, realmente quieres ser invariante a las transformaciones que se utilizan para usar esa entrada.

¿Qué importancia ha tenido la invarianza?

La invariancia ha sido la palabra clave para el aprendizaje de las características. Algo como SIFT, que es un rasgo artesanal bastante popular donde insertamos aquí es transferido invariante. Y las redes de supervisión, por ejemplo, las redes de Alex supervisadas, están entrenadas para ser aumento de datos invariantes. Quieres que esta red clasifique diferentes cultivos o diferentes rotaciones de esta imagen como un árbol, en lugar de pedirle que prediga cuál fue exactamente la transformación aplicada para la entrada.

ARPI

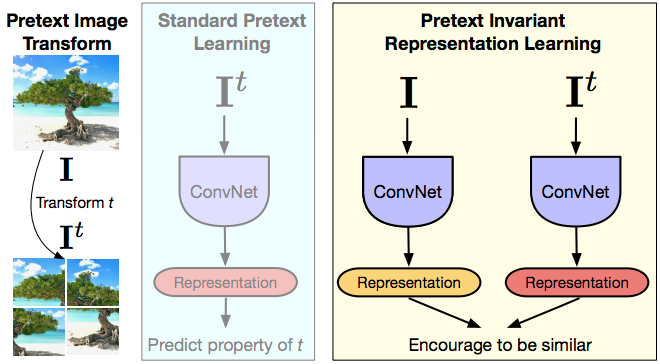
Fig. 15: ARPI

Esto es lo que inspiró a ARPI. Así que ARPI significa aprendizaje de representación de pretexto invariante, donde la idea es que quieres que la representación sea invariante o capturar la menor información posible de la transformación de entrada. Así que tienes la imagen, tienes la versión transformada de la imagen, alimentas ambas imágenes a través de una ConvNet, obtienes una representación y luego básicamente fomentas que estas representaciones sean similares. En términos de la notación mencionada anteriormente, la imagen $I$ y cualquier versión transformada del pretexto de esta imagen $I^t$ son muestras relacionadas y cualquier otra imagen son muestras infravaloradas. Así que de esta manera, cuando enmarcas esta red, la representación contiene con suerte muy poca información sobre esta transformación $t$. Y supongan que están usando aprendizaje contrastivo. Así que la parte de aprendizaje contrastivo es básicamente que tienes la característica guardada $v_I$ que viene de la imagen original $I$ y tienes la característica $v_{I^t}$ que viene de la versión transformada y quieres que ambas representaciones sean iguales. Y el artículo del libro que vimos tiene dos estados diferentes del arte de las transformaciones de pretexto, que es el rompecabezas y el método de rotación discutido anteriormente. De alguna manera, esto es como un aprendizaje multitarea, pero no tratando de predecir ambas rotaciones diseñadas. Estás tratando de ser invariante de la rotación del rompecabezas.

Usando un gran número de negativos

La clave que ha hecho que el aprendizaje contrastivo funcione bien en el pasado, haciendo intentos exitosos, es utilizar un gran número de negativos. Uno de los buenos artículos que han tenido éxito es el artículo de discriminación de 2018, que introdujo este concepto de un banco de memoria. Este es potenciado, la mayoría de los métodos de investigación que son técnicas de vanguardia dependen de esta idea de un banco de memoria. El banco de memoria es una buena manera de obtener un gran número de negativos sin aumentar realmente el tipo de requisitos computacionales. Lo que se hace es almacenar un vector de característica por imagen en la memoria, y luego se utiliza ese vector de característica en su aprendizaje contrastivo.

Como funciona

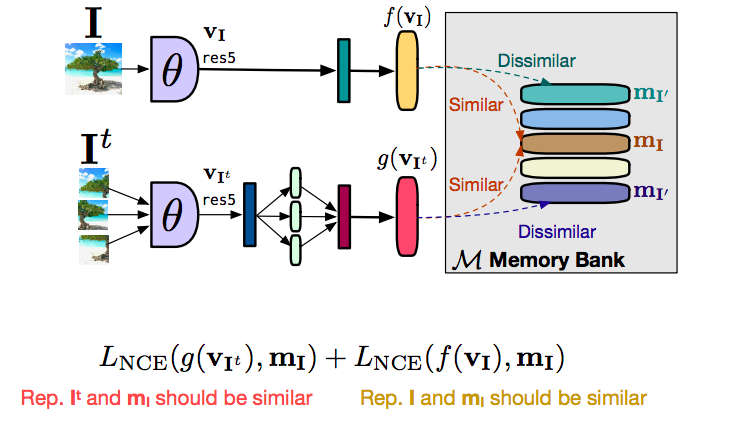
Fig. 16: Cómo funciona el Banco de Memoria

Hablemos primero de cómo harías toda esta configuración del ARPI sin usar un banco de memoria. Así que tienes una imagen $I$ y tienes una imagen $I^t$, y retroalimentas ambas imágenes, obtienes un vector de características $f(v_I)$ de la imagen original $I$, obtienes una característica $g(v_{I^t})$ de las versiones transformadas, los parches, en este caso. Lo que quieres es que las características $f$ y $g$ sean similares. Y quieres que las características de cualquier otra imagen no relacionada sean básicamente diferentes. En este caso, lo que podemos hacer ahora es que si quieres muchos negativos, realmente querríamos que muchas de estas imágenes negativas se retroalimentaran al mismo tiempo, lo que realmente significa que se necesita un tamaño de lote muy grande para poder hacer esto. Por supuesto, un gran tamaño de lote no es realmente bueno, si no es posible, en una cantidad limitada de memoria de la GPU. La forma de hacerlo es usar algo llamado banco de memoria. Así que lo que este banco de memoria hace es que almacena un vector de característica para cada una de las imágenes en su conjunto de datos, y cuando usted está haciendo el aprendizaje contrastivo en lugar de utilizar vectores de característica, digamos, de una imagen diferente de un negativo o una imagen diferente en su lote, usted puede simplemente recuperar estas características de la memoria. Puedes recuperar características de cualquier otra imagen no relacionada de la memoria y puedes sustituirla para llevar a cabo un aprendizaje contrastivo. Simplemente dividiendo el objetivo en dos partes, había un término contrastado para traer el vector de la característica de la imagen transformada $g(v_I)$, similar a la representación que tenemos en la memoria así $m_I$. Y de forma similar, tenemos un segundo término contrastivo que intenta acercar el rasgo $f(v_I)$ a la representación del rasgo que tenemos en la memoria. Esencialmente $g$ se acerca a $m_I$ y $f$ se acerca a $m_I$. Por la transitividad, $f$ y $g$ se acercan el uno al otro. Y la razón para separar esto fue que estabilizó el entrenamiento y no fuimos capaces de entrenar sin hacer esto. Básicamente, el entrenamiento no convergía realmente. Al separar esto en dos formas, en lugar de hacer un aprendizaje directo contrastivo entre $f$ y $g$, fuimos capaces de estabilizar el entrenamiento y hacerlo funcionar.

Preentrenamiento ARPI

La forma de evaluar esto es básicamente mediante un sistema estándar de evaluación previa al entrenamiento. Para el aprendizaje de transferencia, podemos pre-entrenar en imágenes sin etiquetas. La forma estándar de hacer esto es tomar una red de imágenes, tirar las etiquetas y fingir que no están supervisadas.

Evaluación

La evaluación puede realizarse mediante un ajuste completo (evaluación de inicialización) o entrenando un clasificador lineal (evaluación de características). La robustez del ARPI ha sido probada mediante el uso de imágenes en distribución entrenándola en imágenes en la naturaleza. Así que acabamos de tomar un millón de imágenes al azar de Flickr, que es el conjunto de datos del YFCC. Y luego básicamente realizamos el preentrenamiento sore estas imágenes y luego realizamos el transplante en diferentes conjuntos de datos.

Evaluando en la tarea de detección de objetos

EL ARPI fue evaluado primero en la tarea de detección de objetos (una tarea estándar en visión) y fue capaz de superar a las redes preentrenadas supervisadas por ImageNet en los conjuntos de datos VOC07+12 y VOC07. De hecho, ARPI superó incluso en los criterios de evaluación más estrictos, $AP^{all}$ y eso es una buena señal positiva.

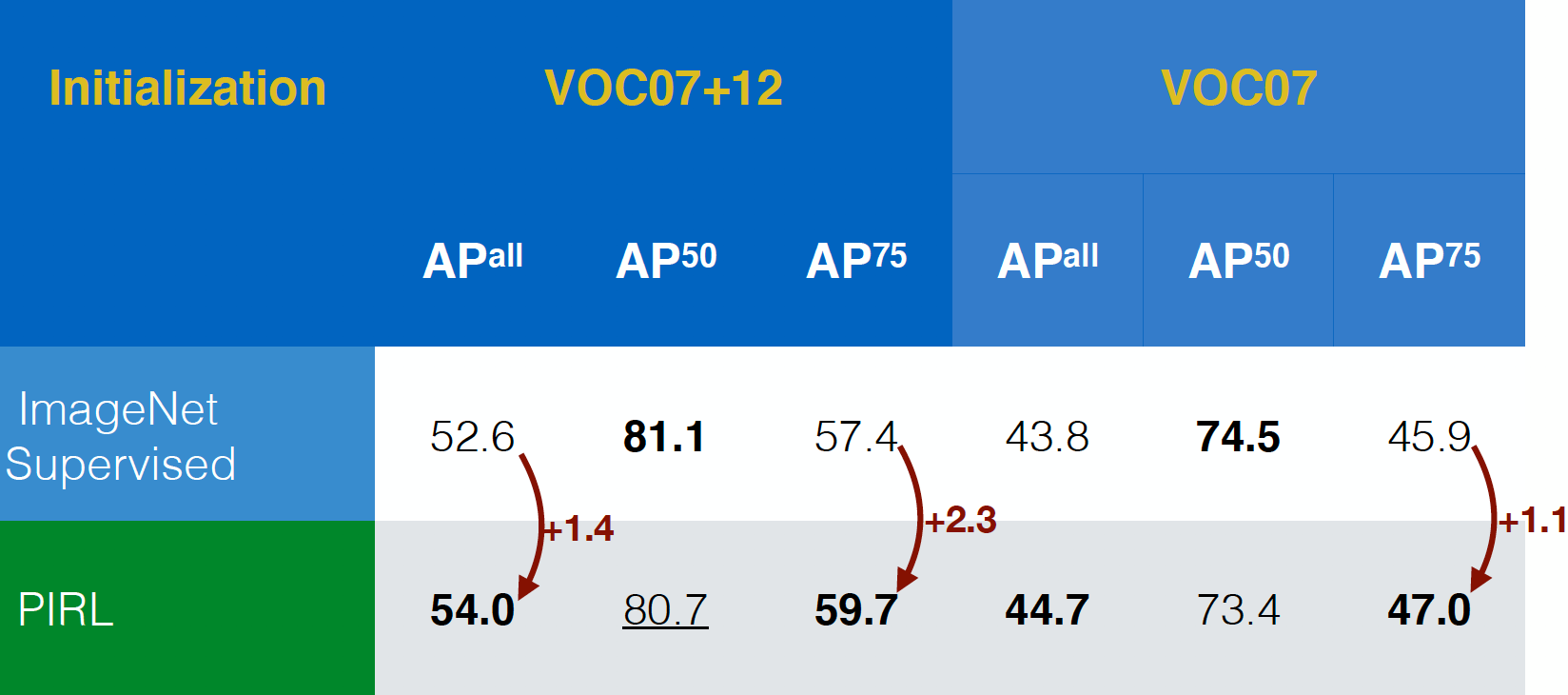
Fig. 17: Rendimiento de la detección de objetos en diferentes conjuntos de datos

Evaluación del aprendizaje semisupervisado

ARPI fue entonces evaluado en una tarea de aprendizaje semisupervisada. Una vez más, ARPI se desempeñó bastante bien. De hecho, ARPI fue mejor que incluso la tarea de pretexto del rompecabezas . La única diferencia entre la primera y la última fila es que ARPI es una versión invariante, mientras que el rompecabezas es una versión covariante.

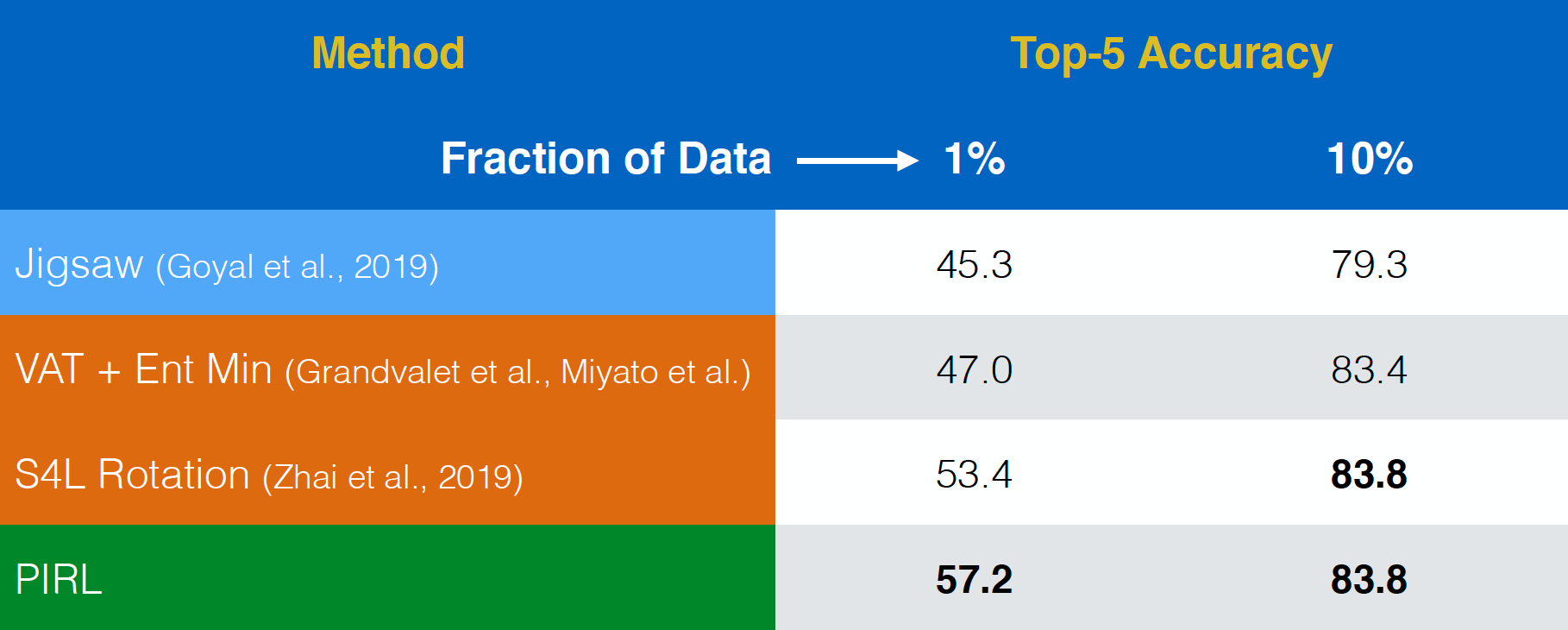
Fig. 18: Aprendizaje semisupervisado en ImageNet

Evaluación de la clasificación lineal

Ahora cuando se evaluan los clasificadores lineales, el ARPI estaba a la par con el CPCv2, cuando este salió. También funcionó bien en un montón de ajustes de parámetros y un montón de diferentes arquitecturas. Y por supuesto, ahora puedes tener un rendimiento bastante bueno con métodos como SimCLR o demás. De hecho, la precisión Top-1 para SimCLR sería de alrededor de 69-70, mientras que para el ARPI, sería de alrededor de 63.

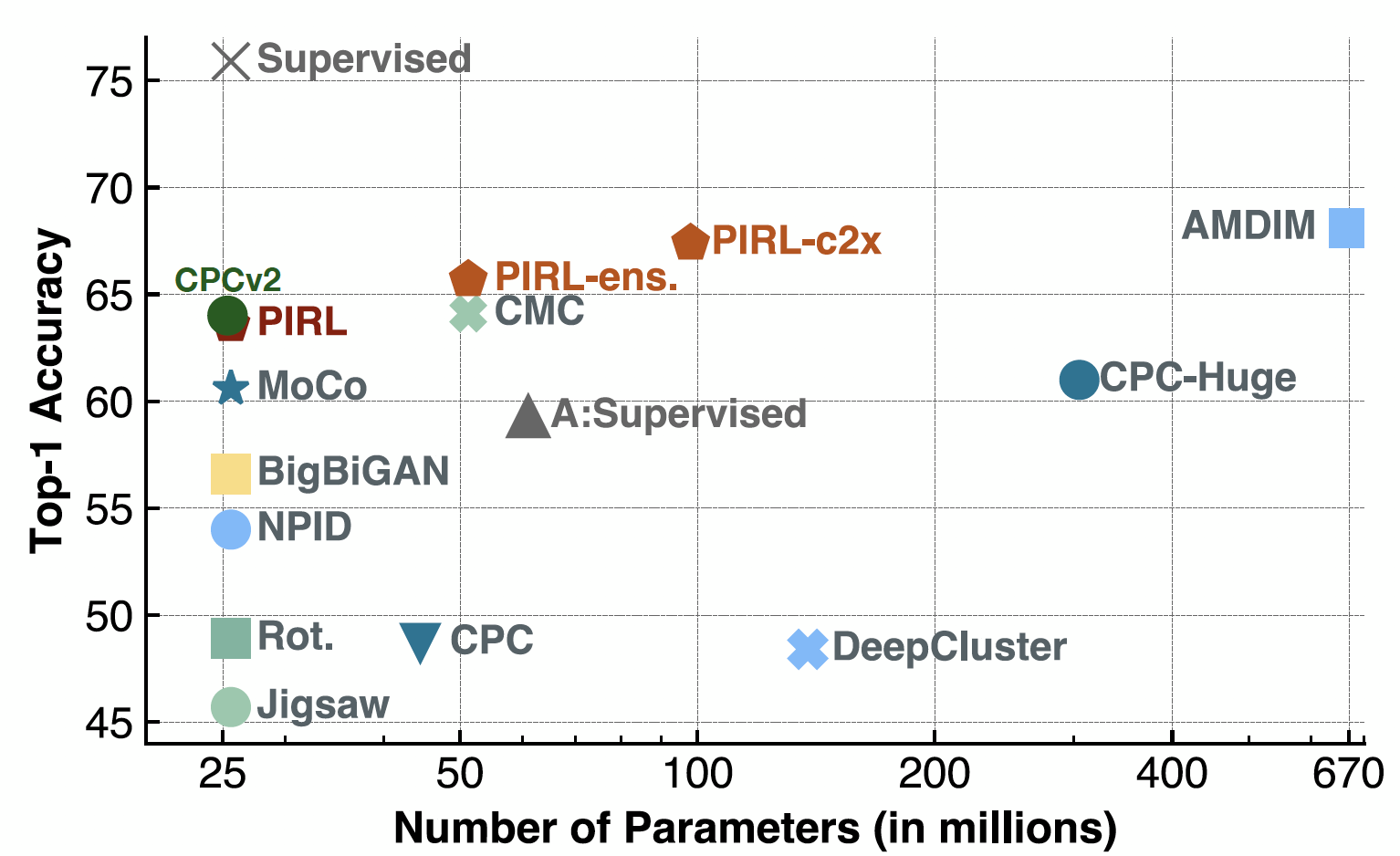
Fig. 19: Clasificación de ImageNet con modelos lineales

Evaluando en las imágenes del YFCC

El ARPI fue evaluado en imágenes de Flickr “In-the-wild” del conjunto de datos del YFCC. Fue capaz de funcionar mejor que el rompecabezas, incluso con un conjunto de datos $100$ veces más pequeño. Esto muestra el poder de tomar en cuenta la invariancia para la representación en las tareas de pretexto, en lugar de sólo predecir las tareas de pretexto.

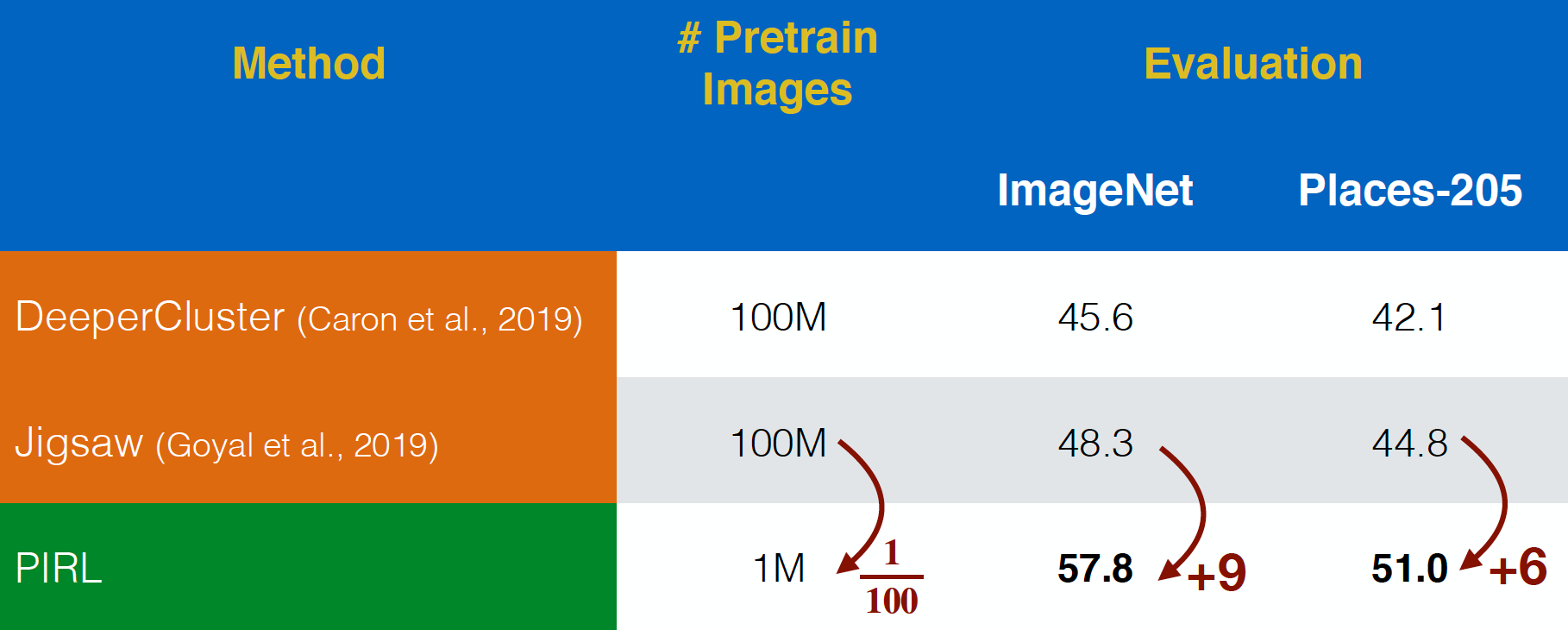
Fig. 20: Preentrenamiento en imágenes no curadas del YFCC

Características semánticas

Ahora, volviendo a la verificación de los características semánticas, miramos la precisión Top-1 para el ARPI y el rompecabezas para diferentes capas de representación desde “conv1” a “res5”. Es interesante observar que la precisión sigue aumentando para las diferentes capas tanto para el ARPI como para el rompecabezas, pero disminuye en la 5ª capa para el rompecabezas. Mientras que, la precisión sigue mejorando para ARPI, i.e., más y más semántica.

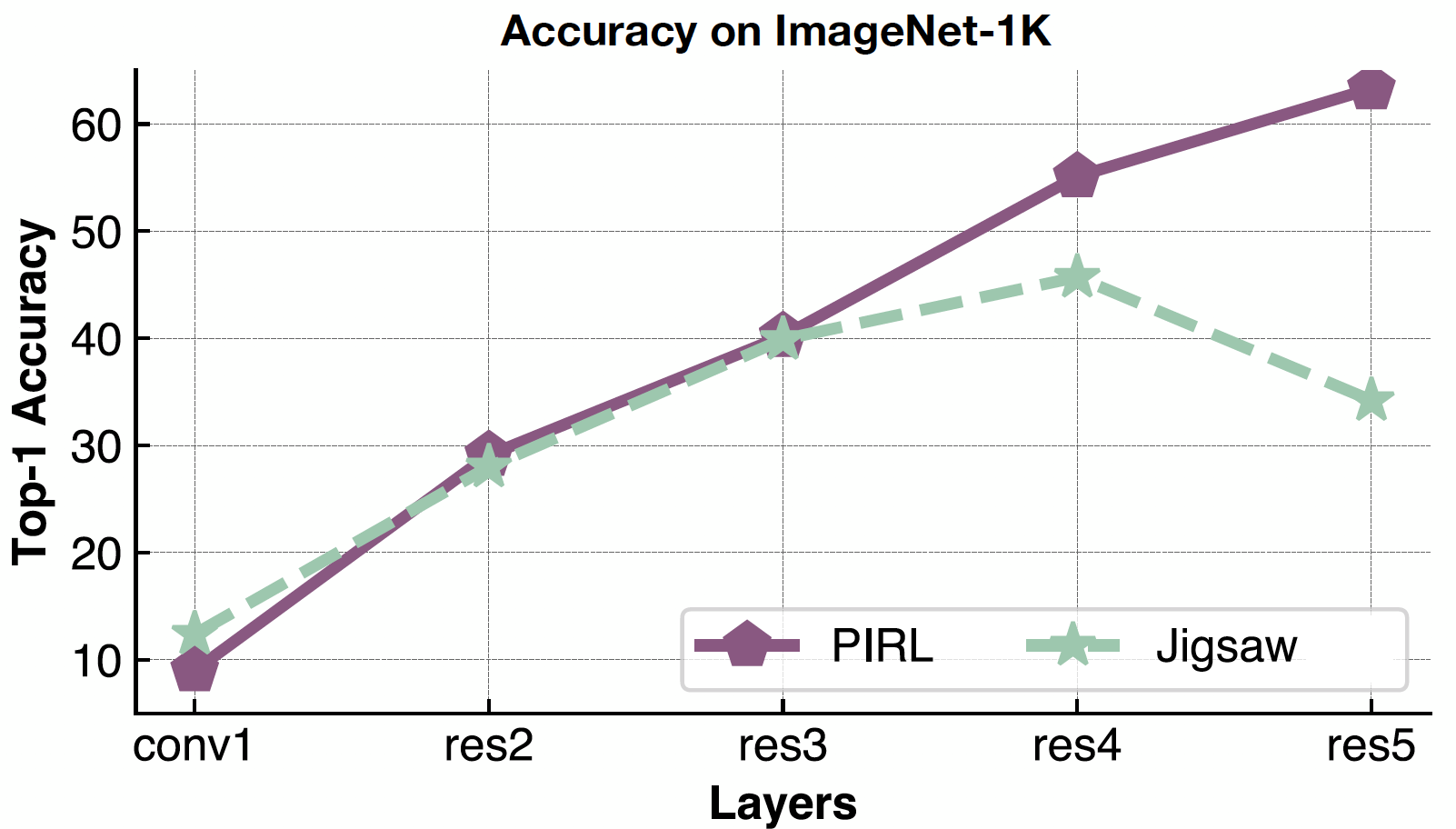
Fig. 21: Calidad de las representaciones del ARPI por capa

Escalabilidad

ARPI es muy bueno en el manejo problemas complejos porque tu nunca predices el número de permutaciones, sólo los usas como entrada. Así que el ARPI puede escalar fácilmente a todas las 362.880 permutaciones posibles en los 9 parches. Mientras que en el rompecabezas, ya que estás prediciendo eso, estás limitado por el tamaño de tu espacio de salida.

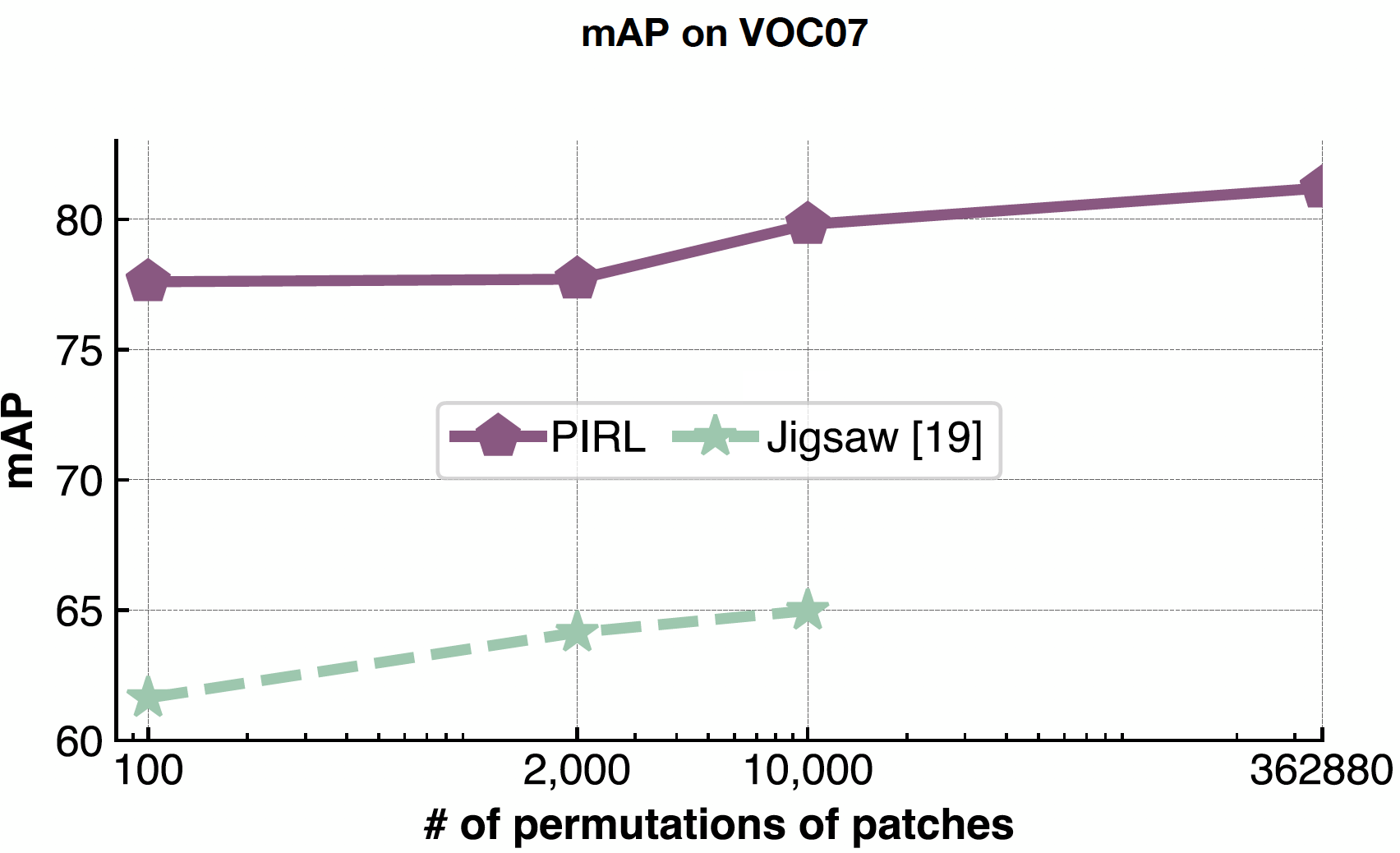
Fig. 22: Efecto de la variación del número de permutaciones de parches

El artículo de “Misra & van der Maaten, 2019, PIRL” también muestra como el ARPI podría extenderse fácilmente a otras tareas de pretexto como el rompecabezas, las rotaciones y así sucesivamente. Además, podría incluso extenderse a combinaciones de esas tareas como Rompecabezas+Rotación.

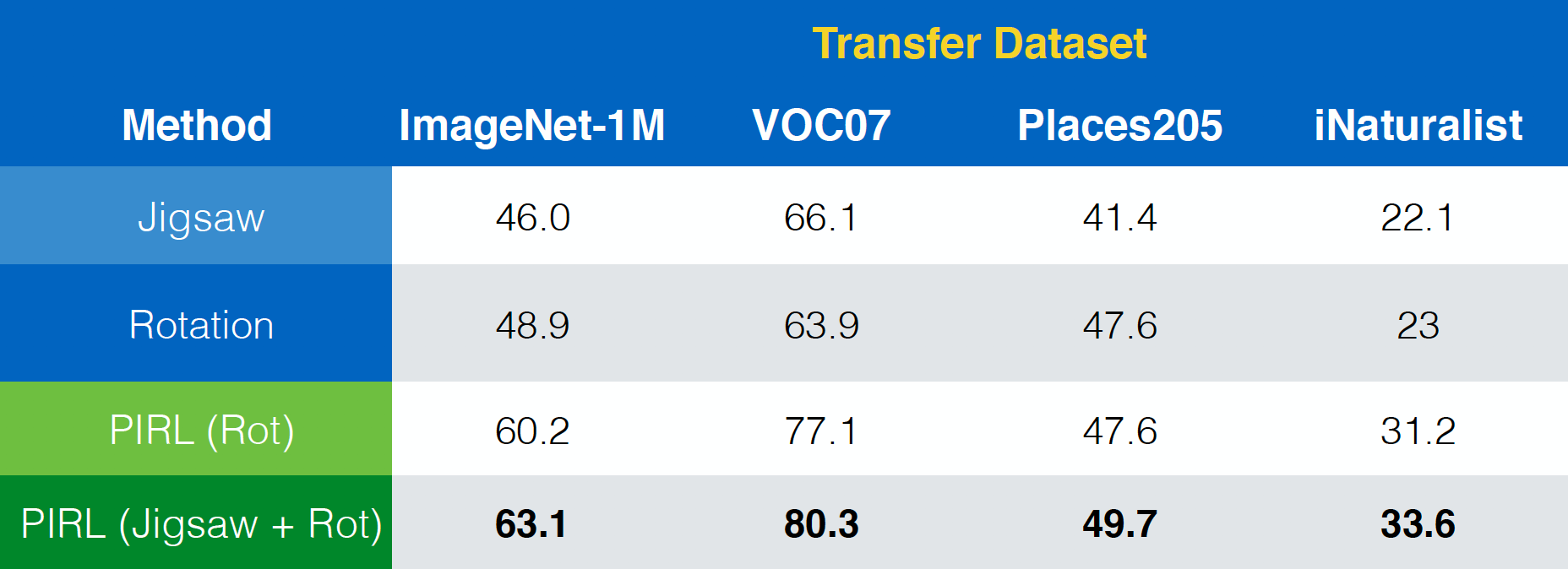
Fig. 23: Usando PIRL con (combinaciones de) diferentes tareas de pretexto

Invariancia vs. desempeño

En cuanto a la propiedad de la invariancia, se podría afirmar, en general, que la invariancia del ARPI es más que la del Agrupamiento, que a su vez tiene más invariancia que la de las tareas de pretexto. Y de forma similar, el desmpeño del ARPI es mayor que el del Agrupamiento, que a su vez tiene un rendimiento mayor que el de las tareas de pretexto. Esto sugiere que tomar más invariancia en su método podría mejorar el rendimiento.

Limitaciones

1. No está muy claro qué conjunto para transformación de datos importa. Aunque el Rompecabezas funciona, no está muy claro por qué funciona.
2. Saturación con el tamaño del modelo y el tamaño de los datos.
3. ¿Qué invariancias importan? (Uno podría pensar en qué invariancias funcionan para una tarea supervisada en general como trabajo futuro).

Así que en general, debemos tratar de predecir más y más información y tratar de ser lo más invariante posible.

Algunas preguntas importantes planteadas como dudas

Aprendizaje contrastivo y normas de lote

1. ¿No aprendería la red sólo una forma muy trivial de separar los negativos de los positivos si la red de contraste utiliza la capa de norma de lote (ya que la información pasaría entonces de una muestra a la otra)?

Resp: En ARPI, no se observó tal fenómeno, así que sólo se utilizó la norma habitual de lotes

1. Entonces, ¿está bien usar normas de lote para cualquier red de contraste?

Resp: *En general, sí. En SimCLR, se utiliza una variante de la norma de lote habitual para emular un gran tamaño de lote. Por lo tanto, la norma de lote con tal vez algunos ajustes podría ser utilizado para hacer el entrenamiento más sencillo *

1. ¿Funciona la norma de lote en el artículo del ARPI sólo porque se implementa como un banco de memoria - ya que todas las representaciones no se toman al mismo tiempo? (Como las normas de lote no se utilizan específicamente en el artículo de MoCo, por ejemplo)

Resp: Sí. En el ARPI, el mismo lote no tiene todas las representaciones y posiblemente por qué la norma del lote funciona aquí, lo que podría no ser el caso para otras tareas donde las representaciones están todas correlacionadas dentro del lote

1. Entonces, aparte del banco de memoria, ¿hay alguna otra sugerencia para la pérdida de n-pares? ¿Deberíamos usar AlexNet u otras que no usen la norma del lote? ¿O hay alguna manera de apagar la capa de norma de lote? (Esto es para una tarea de aprendizaje de video)

Resp: Generalmente los recuadros están correlacionados en los videos, y el desempeño de la norma del lote se degrada cuando hay correlaciones. Además, incluso la implementación más simple de AlexNet de hecho utiliza la norma de lote. Porque, es mucho más estable cuando se entrena con una norma de lote. Incluso se puede utilizar una tasa de aprendizaje más alta y que también se podría utilizar para otras tareas posteriores. Podrías usar una variante de la norma por lotes, por ejemplo, la norma de grupo para la tarea de aprendizaje de vídeo, ya que no depende del tamaño del lote.

Funciones de pérdida en el ARPI

1. En el ARPI, ¿por qué se utiliza el ECR (Estimador Contrastativo de Ruido) para minimizar la pérdida y no sólo la probabilidad negativa de la distribución de datos: $h(v_{I},v_{I^{t})$?

Resp: Realmente, ambos podrían ser usados. La razón para usar el ECR tiene más que ver con la forma en que el fue configurado en el artículo del libro. Así que, con $k+1$ negativos, es equivalente a resolver el problema binario de $k+1$. Otra forma de hacerlo es empleando un softmax, donde se aplica un softmax y se minimiza la probabilidad negativa

Consejos relacionados con el proyecto de aprendizaje auto-supervisado

¿Cómo hacemos que funcione un simple modelo auto-supervisado? ¿Cómo comenzamos la implementación?

Resp: Hay una cierta clase de técnicas que son útiles para las etapas iniciales. Por ejemplo, podrías mirar las tareas de pretexto. La rotación es una tarea muy fácil de implementar. El número de piezas móviles es en general un buen indicador. Si estás planeando implementar un método existente, entonces podrías tener que mirar más de cerca los detalles mencionados por los autores, como - la tasa exacta de aprendizaje utilizada, la forma en que se utilizaron las normas de lote, etc. Cuantas más cosas de estas, más difícil será la implementación. La siguiente cosa muy crítica a considerar es el aumento de los datos. Si consigues que algo funcione, entonces añade más aumento de datos a esta.

Modelos Generativos

¿Ha pensado en combinar modelos generativos con redes contrastadas?

Resp: *Generalmente, es buena idea. Pero no se ha implementado en parte porque es difícil y no trivial entrenar tales modelos. Los enfoques integradores son más difíciles de implementar, pero quizás sea el camino a seguir en el futuro.

Destilación

¿No aumentaría la incertidumbre del modelo cuando los objetivos más ricos son dados por distribuciones más suaves? Además, ¿por qué se llama destilación?

Resp: Si entrenas con etiquetas one hot, tus modelos tienden a ser extremadamente confiados. Trucos como la suavización de la etiqueta se están utilizando en algunos métodos. La suavización de etiquetas es sólo una versión simple de la destilación en la que se intenta predecir un vector one hot. Ahora, en lugar de tratar de predecir todo el vector one hot de un uno, sacas alguna masa de probabilidad de eso, donde en lugar de predecir un uno y un montón de ceros, predices digamos $0,97$ y luego añades $0,01$, $0,01$ y $0,01$ al vector restante (uniformemente). La destilación es sólo una forma más informada de hacer esto. En lugar de aumentar aleatoriamente la probabilidad de una tarea no relacionada, tienes una red preentrenada para hacerlo. En general, las distribuciones más suaves son muy útiles en los métodos de pre-entrenamiento. Los modelos tienden a ser demasiado confiados y por lo tanto las distribuciones más suaves son más fáciles de entrenar. También convergen más rápidamente. Estos beneficios están presentes en la destilación