Redes generativas adversarias

Introducción a las redes generativas adversarias (GANs)

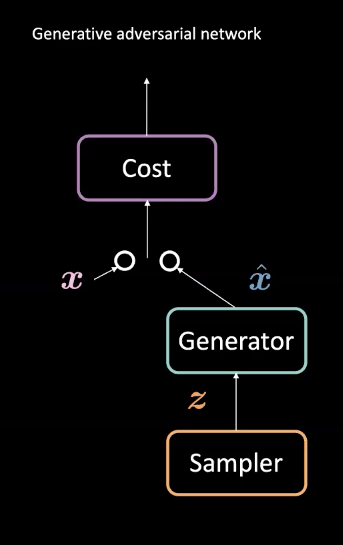
Fig. 1: Arquitectura GAN

Las GAN son un tipo de red neuronal que se utiliza para el aprendizaje automático no supervisado. Se componen de dos módulos adversarios: redes generador y de costo. Estos módulos compiten entre sí de modo que la red de costo intenta filtrar ejemplos falsos mientras que el generador intenta engañar a este filtro creando ejemplos realistas $\vect{\hat{x}}$. A través de esta competencia, el modelo aprende un generador que crea datos realistas. Se pueden usar en tareas como predicciones futuras o para generar imágenes después de haber sido entrenadas en un conjunto de datos en particular.

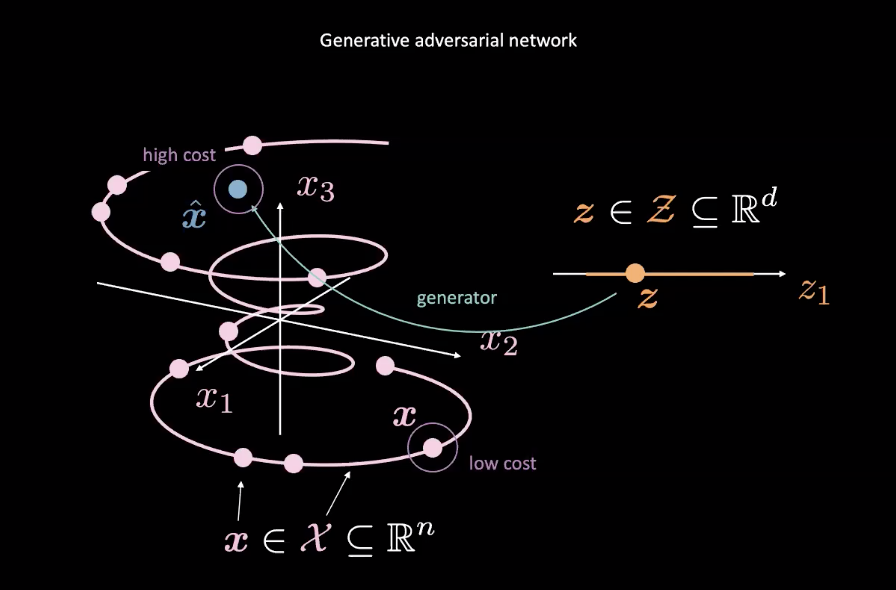
Fig. 2: Asignación de GAN a partir de una variable aleatoria

Las GAN son ejemplos de modelos basados ​​en energía (EBM). Como tal, la red de costos está entrenada para producir costos bajos para entradas más cercanas a la distribución de datos real indicada por el $\vect{x}$ rosa en la Fig. 2. Datos de otras distribuciones, como el $\vect{\hat{x}}$ en la Fig. 2, debería tener un costo elevado. Por lo general, se utiliza una pérdida del cuadrado medio del error (MSE) para calcular el rendimiento de la red de costos. Vale la pena señalar que la función de costo genera un valor escalar positivo dentro de un rango específico es decir, $\text{cost} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$). Esto es diferente a un discriminador clásico que usa clasificación discreta para sus salidas.

Mientras tanto, la red del generador ($\text{generator} : \mathcal{Z} \rightarrow \mathbb{R}^n$) está entrenada para mejorar su mapeo de la variable aleatoria $\vect{z}$ a datos generados realistas $\vect{\hat{x}}$ para engañar a la red de costos. El generador se entrena con respecto a la salida de la red de costos, tratando de minimizar la energía de $\vect{\hat{x}}$. Denotamos esta energía como $C(G(\vect{z}))$, donde $C(\cdot)$ es la red de costos y $G(\cdot)$ es la red del generador.

El entrenamiento de la red de costos se basa en minimizar la pérdida de MSE, mientras que el entrenamiento de la red de generadores es minimizando la red de costos, utilizando gradientes de $C(\vect{\hat{x}})$ con respecto a $\vect{\hat{x}}$.

Para asegurar que se asigne un alto costo a los puntos fuera del colector de datos y un bajo costo a los puntos dentro de él, la función de pérdida para la red de costos $\mathcal{L}_{C}$ is $C(x)+[m-C(G(\vect{z}))]^+$ para un margen positivo $m$. Minimizar $\mathcal{L}_{C}$ requiere que $C(\vect{x}) \rightarrow 0$ y $C(G(\vect{z})) \rightarrow m$. La pérdida para el generador $\mathcal{L}_{G}$ es simplemente $C(G(\vect{z}))$, lo que anima al generador a asegurarse de que $C(G(\vect{z})) \rightarrow 0$. Sin embargo, esto crea inestabilidad como $0 \leftarrow C(G(\vect{z})) \rightarrow m$.

Diferencias entre GANs y VAEs

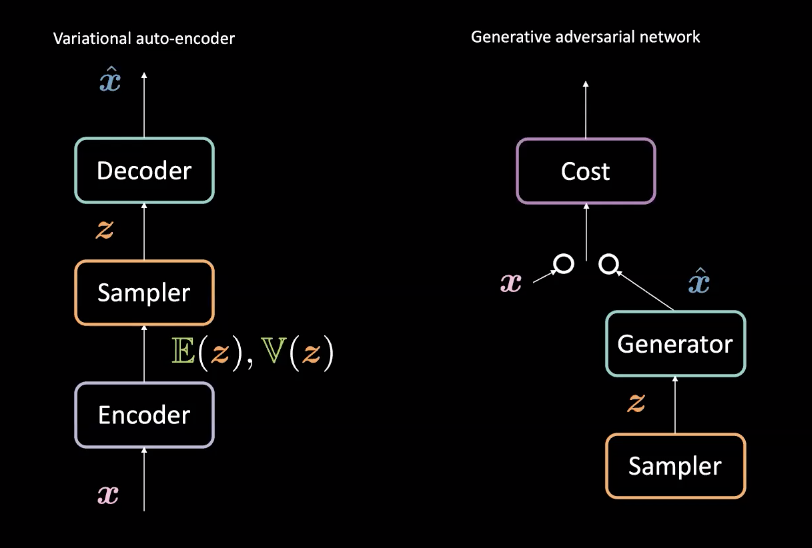
Fig. 3: VAE (izquierda) *vs.* GAN (derecha) - Diseño de Arquitectura

En comparación con los codificadores automáticos variacionales (VAE) de la semana 8, los GAN crean generadores de manera ligeramente diferente. Recuerde, los VAE mapean las entradas $\vect{x}$ a un espacio latente $\mathcal{Z}$ con un codificador y luego mapean desde $\mathcal{Z}$ de regreso al espacio de datos con un descifrador para obtener $\vect{\hat{x}}$. Luego usan la pérdida de reconstrucción para hacer que $\vect{x}$ y $\vect{\hat{x}}$ sean similares. Las GAN, por otro lado, se entrenan a través de un entorno de confrontación con el generador y las redes de costos compitiendo como se describe anteriormente. Estas redes se entrenan sucesivamente mediante retropropagación mediante métodos basados ​​en gradientes. La comparación de esta diferencia arquitectónica se puede ver en la Fig.3.

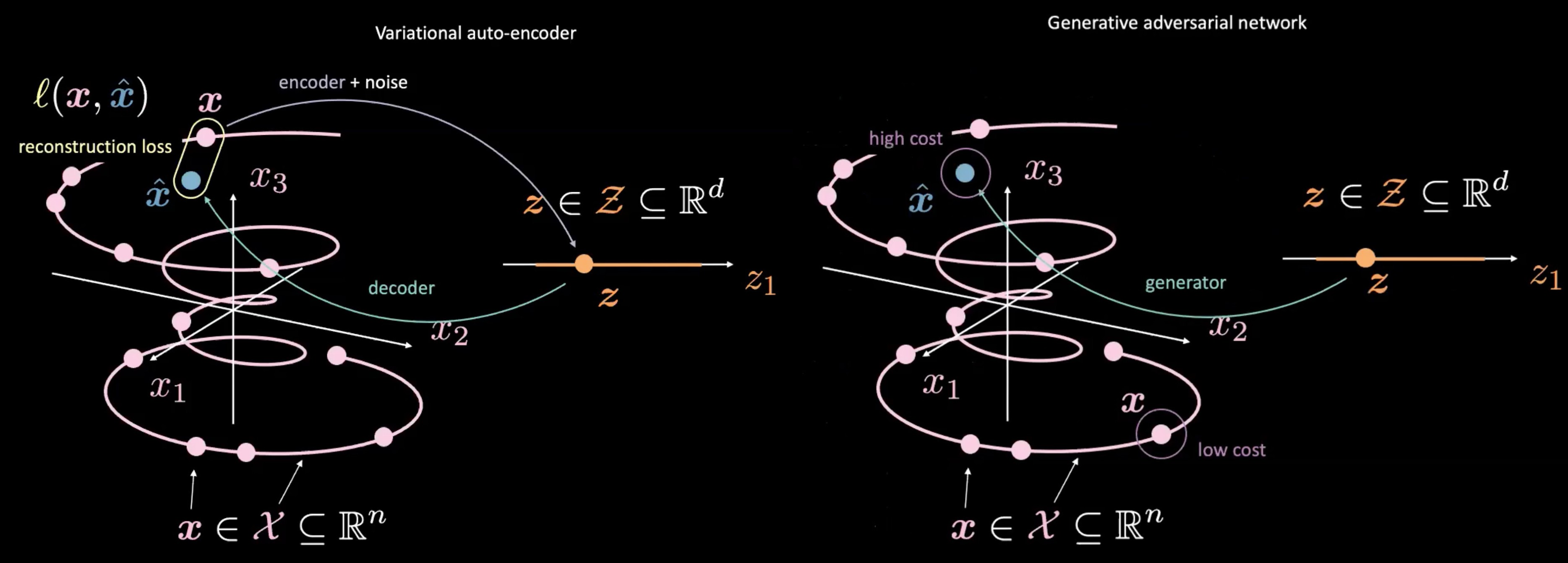
Fig. 4: VAE (left) *vs.* GAN (right) - Asignación de una muestra aleatoria $\vect{z}$

Los GAN también se diferencian de los VAE en la forma en que producen y usan $\vect{z}$. Las GAN comienzan muestreando $\vect{z}$, similar al espacio latente en un VAE. Luego usan una red generativa para mapear $\vect{z}$ a $\vect{\hat{x}}$. Este $\vect{\hat{x}}$ se envía luego a través de una red discriminadora / de costos para evaluar qué tan “real” es. Una de las principales diferencias de VAE y GAN es que ** no necesitamos medir una relación directa (* es decir, * pérdida de reconstrucción) entre la salida de la red generativa $\vect{\hat{x}}$ y los datos reales $\vect{x}$. ** En su lugar, forzamos $\vect{\hat{x}}$ a ser similar a $\vect{x}$ al entrenar el generador para producir $\vect{\hat{x}}$ tal que la red discriminadora / de costos produzca puntuaciones que sean similares a las de los datos reales $\vect{x}$, o más “reales”.

Principales dificultades en las GAN

Si bien las GAN pueden ser poderosas para construir generadores, tienen algunas dificultades importantes.

1. Convergencia inestable

A medida que el generador mejora con el entrenamiento, el rendimiento del discriminador empeora porque el discriminador ya no puede diferenciar fácilmente entre datos reales y falsos. Si el generador es perfecto, entonces la variedad de datos reales y falsos se superpondrán y el discriminador creará muchas clasificaciones erróneas.

Esto plantea un problema para la convergencia de la GAN: la retroalimentación del discriminador se vuelve menos significativa con el tiempo. Si el GAN ​​continúa entrenando más allá del punto en el que el discriminador está dando retroalimentación completamente aleatoria, entonces el generador comienza a entrenar con retroalimentación basura y su calidad puede colapsar. [Consulte [formación de convergencia en GAN] (https://developers.google.com/machine-learning/gan/training)]

Como resultado de esta naturaleza antagónica entre el generador y el discriminador, hay un punto de equilibrio inestable en lugar de un equilibrio.

1. Desvanecimiento de gradiente

Consideremos usar la pérdida de entropía cruzada binaria para una GAN:

A medida que el discriminador se vuelve más seguro, $D(\vect{x})$ $ se acerca a $1$ y $D(\vect{\hat{x}})$ se acerca a $0$. Esta confianza mueve los resultados de la red de costos a regiones más planas donde los gradientes se vuelven más saturados. Estas regiones más planas proporcionan pequeños gradientes que se desvanecen y dificultan el entrenamiento de la red de generadores. Por lo tanto, al entrenar a un GAN, debe asegurarse de que el costo aumente gradualmente a medida que adquiere más confianza.

3. Colapso de la moda

Si un generador mapea todos los $\vect{z}$ del muestreador a un ** único ** $\vect{\hat{x}}$ que puede engañar al discriminador, entonces el generador producirá solo ese $\vect{\hat{x}}$. Eventualmente, el discriminador aprenderá a detectar específicamente esta entrada falsa. Como resultado, el generador simplemente encuentra el siguiente $\vect{\hat{x}}$ más plausible y el ciclo continúa. En consecuencia, el discriminador queda atrapado en los mínimos locales mientras recorre los $\vect{\hat{x}}$ falsos. Una posible solución a este problema es imponer alguna penalización al generador por dar siempre la misma salida dadas diferentes entradas.

[Código fuente de Deep Convolutional Generative Adversarial Network (DCGAN)] (https://www.youtube.com/watch?v=xYc11zyZ26M&t=2911s)

El código fuente del ejemplo se puede encontrar [aquí] (https://github.com/pytorch/examples/blob/master/dcgan/main.py).

Generador

1. El generador muestra la entrada utilizando varios módulos nn.ConvTranspose2d separados por nn.BatchNorm2d y nn.ReLU.
2. Al final de la secuencia, la red usa nn.Tanh() para aplastar las salidas a $(- 1,1)$.
3. El vector aleatorio de entrada tiene un tamaño $nz$. La salida tiene un tamaño $nc \times 64 \times 64$, donde $nc$ es el número de canales.

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # la entrada es Z, entrando en una convolución
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # tamaño del estado. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # tamaño del estado. (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # tamaño del estado. (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # tamaño del estado. (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # tamaño del estado. (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

Discriminador

1. Es importante utilizar nn.LeakyReLU como función de activación para evitar matar los gradientes en las regiones negativas. Sin estos gradientes, el generador no recibirá actualizaciones.
2. Al final de la secuencia, el discriminador usa nn.Sigmoid () para clasificar la entrada

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # la entrada es (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # tamaño del estado. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # tamaño del estado. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # tamaño del estado. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # tamaño del estado. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

Estas dos clases se inicializan como netG y netD

Función de pérdida para GAN

Usamos entropía cruzada binaria (BCE) entre el objetivo y la salida.

criterion = nn.BCELoss()

Preparación

Configuramos Fixed_noise de tamaño opt.batchSize y la longitud del vector aleatorio nz. También creamos etiquetas para datos reales y datos generados (falsos) llamados real_label y fake_label, respectivamente.

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

Luego configuramos optimizadores para redes discriminadoras y generadoras.

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

Entrenamiento

Cada época de entrenamiento esta divida en dos partes.

El paso 1 es actualizar la red discriminadora. Esto se hace en dos partes. Primero, alimentamos los datos reales del discriminador provenientes de los “dataloaders”, calculamos la pérdida entre la salida y la “etiqueta_real”, y luego acumulamos gradientes con propagación hacia atrás. En segundo lugar, alimentamos los datos del discriminador generados por la red del generador utilizando el Fixed_noise, calculamos la pérdida entre la salida y la fake_label, y luego acumulamos el gradiente. Finalmente, usamos los gradientes acumulados para actualizar los parámetros de la red discriminadora.

Tenga en cuenta que separamos los datos falsos para evitar que los gradientes se propaguen al generador mientras entrenamos al discriminador.

También tenga en cuenta que solo necesitamos llamar a zero_grad() una vez al principio para borrar los gradientes de forma que los gradientes de los datos reales y falsos se puedan usar para la actualización. Las dos llamadas .backward() acumulan estos gradientes. Finalmente solo necesitamos una llamada a optimizerD.step () para actualizar los parámetros.

# entrenar con reales
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# entrenar con falsos
noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

El paso 2 es actualizar la red del generador. Esta vez, alimentamos al discriminador con los datos falsos, ¡pero calculamos la pérdida con el real_label! El propósito de hacer esto es entrenar al generador para hacer $\vect{\hat{x}}$ realistas.

netG.zero_grad()
label.fill_(real_label)  # las etiquetras falsas son para los costos del generador
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()