Modelos Mundiales y Redes Generativas Adversarias

Modelos mundiales para el control autónomo

Uno de los usos más importantes de el aprendizaje auto-supervisado es aprender modelos mundiales para control. Cuando los humanos realizan una tarea, tenemos un modelo interno de cómo el mundo funciona. Por ejemplo, nosotros ganamos una intuición física cuando tenemos alrededor de nueve meses, principalmente a través de la observación. En cierto sentido, ésto es similar al aprendizaje auto-supervisado; en aprender a predecir qué pasará, aprendemos principios abstractos, justo como los modelos auto-supervisados aprenden características latentes. Pero yendo un paso más allá, los modelos internos nos permiten actuar sobre el mundo. Por ejemplo, podemos usar nuestra intuición física aprendida y nuestra comprensión aprendida de cómo funcionan nuestros músculos para predecir — y ejecutar — cómo atrapar una pluma que cae.

¿Qué es un “modelo mundial?

Un sistema de inteligencia autónomo comprende cuatro módulos principales (Figura 1.). Primero, el módulo de percepción observa el mundo y calcula una representación del estado del mundo. Esta representación está incompleta porque 1) el agente no observa todo el universo y 2) la precisión de las observaciones es limitada. También vale la pena señalar que en el modelo feed-forward(de retroalimentación hacia adelante), el módulo de percepción solo está presente para el paso de tiempo inicial. En segundo lugar, el módulo de actores (también llamado módulo de políticas) imagina tomar alguna acción basada en el estado (representado) del mundo. En tercer lugar, el módulo de modelo predice el resultado de la acción dado el estado (representado) del mundo, y también posiblemente dadas algunas características latentes. Ésta predicción pasa hacia adelante en el siguiente paso de tiempo como la suposición para el próximo estado del mundo, asumiendo el papel del módulo de percepción del paso de tiempo inicial. La figura 2 ofrece una demostración detallada de este proceso de retroalimentación hacia adelante. Finalmente, el módulo crítico convierte esa misma predicción en un costo de realizar la acción propuesta, e.j, dada la velocidad con la que creo que el bolígrafo está cayendo, si muevo los músculos de esta manera en particular, ¿Qué tanto perderé su captura?

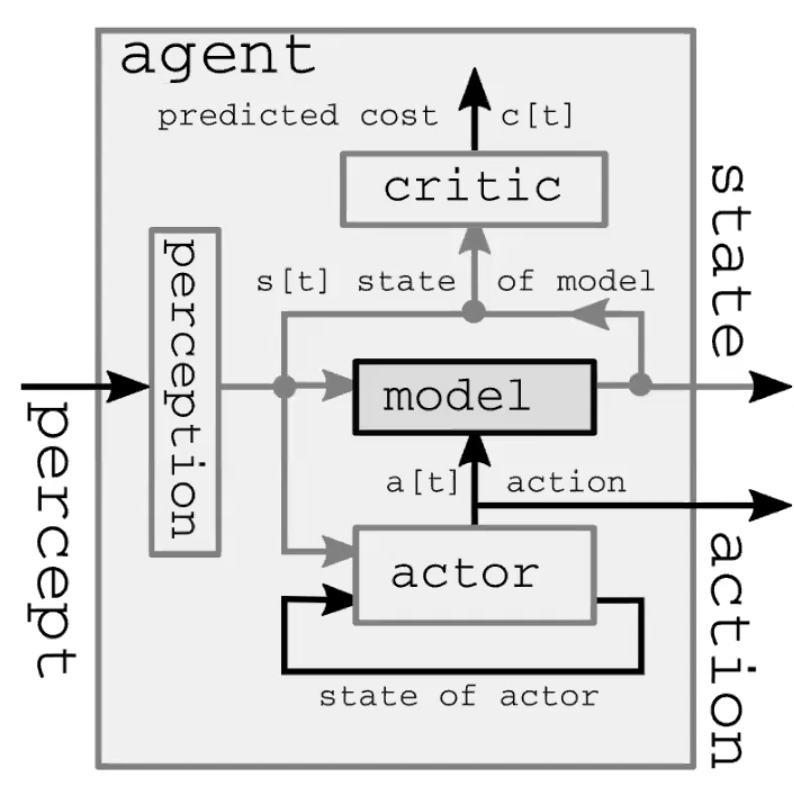
Fig. 1: La arquitectura de los Modelos Mundiales de una demostración de un sistema de inteligencia autónoma.

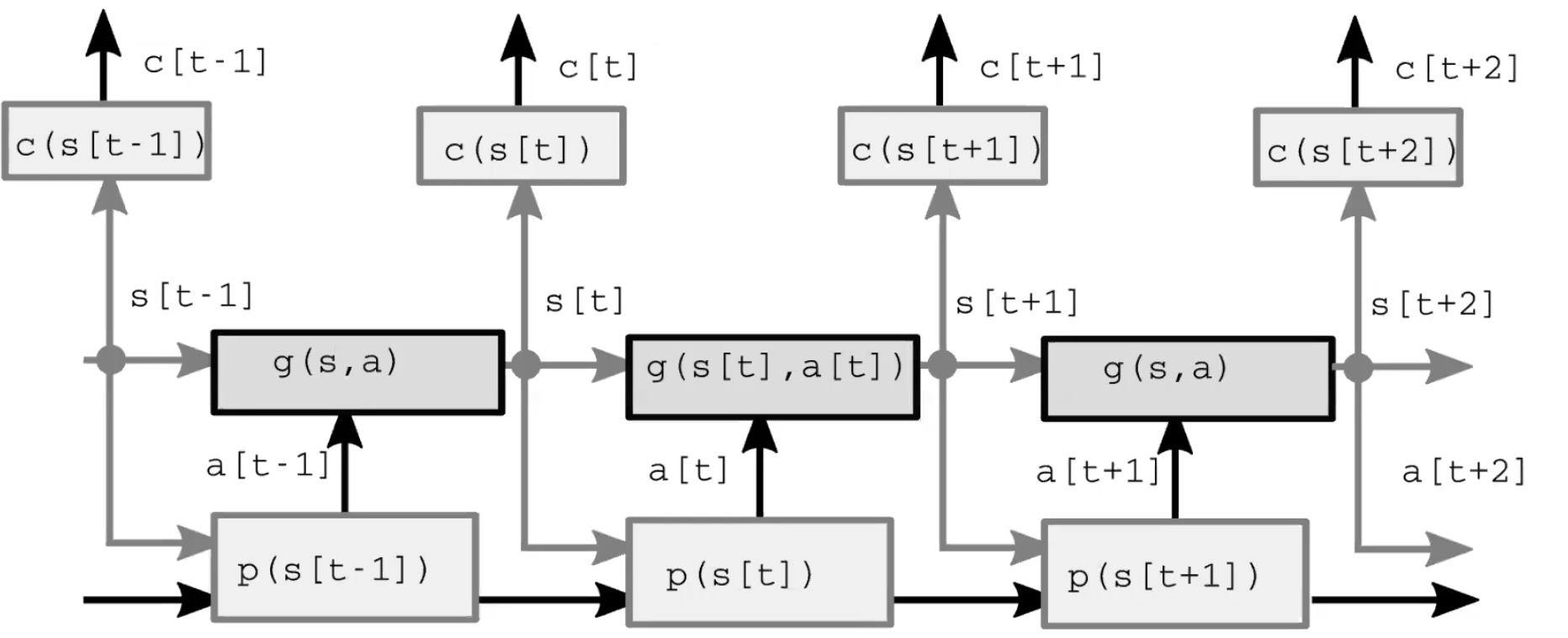
Fig. 2: Arquitectura del modelo.

La configuración clásica

En el control óptimo clásico, no hay un módulo de actor / política, sino solo una variable de acción. Esta formulación está optimizada por un método clásico llamado Modelo Predictivo de Control, que fue utilizado por la NASA en la década de 1960 para calcular las trayectorias de los cohetes cuando cambiaron de computadoras humanas (en su mayoría mujeres matemáticas negras) a computadoras electrónicas. Podemos pensar en este sistema como un RNN desenrollado, y las acciones como variables latentes, y usar métodos de retropropagación y gradiente (o posiblemente otros métodos, como la programación dinámica para un conjunto de acciones discretas) para inferir la secuencia de acciones que minimiza la suma de los costos de los pasos de tiempo

Apartado: usamos la palabra “inferencia” para las variables latentes y “aprendizaje” para los parámetros, aunque el proceso de optimización es generalmente similar. Una diferencia importante es que una variable latente toma un valor específico para cada muestra, mientras que los parámetros se comparten entre las muestras.

Una mejora

Ahora, preferiríamos no pasar por el complicado proceso de retropropagación cada vez que queremos hacer un plan. Para abordar esto, usamos el mismo truco que usamos para el codificador automátco variacional para mejorar la codificación esparcida: entrenamos un codificador para predecir directamente la secuencia de acción óptima a partir de las representaciones del mundo. En este régimen, el codificador se denomina red de políticas.

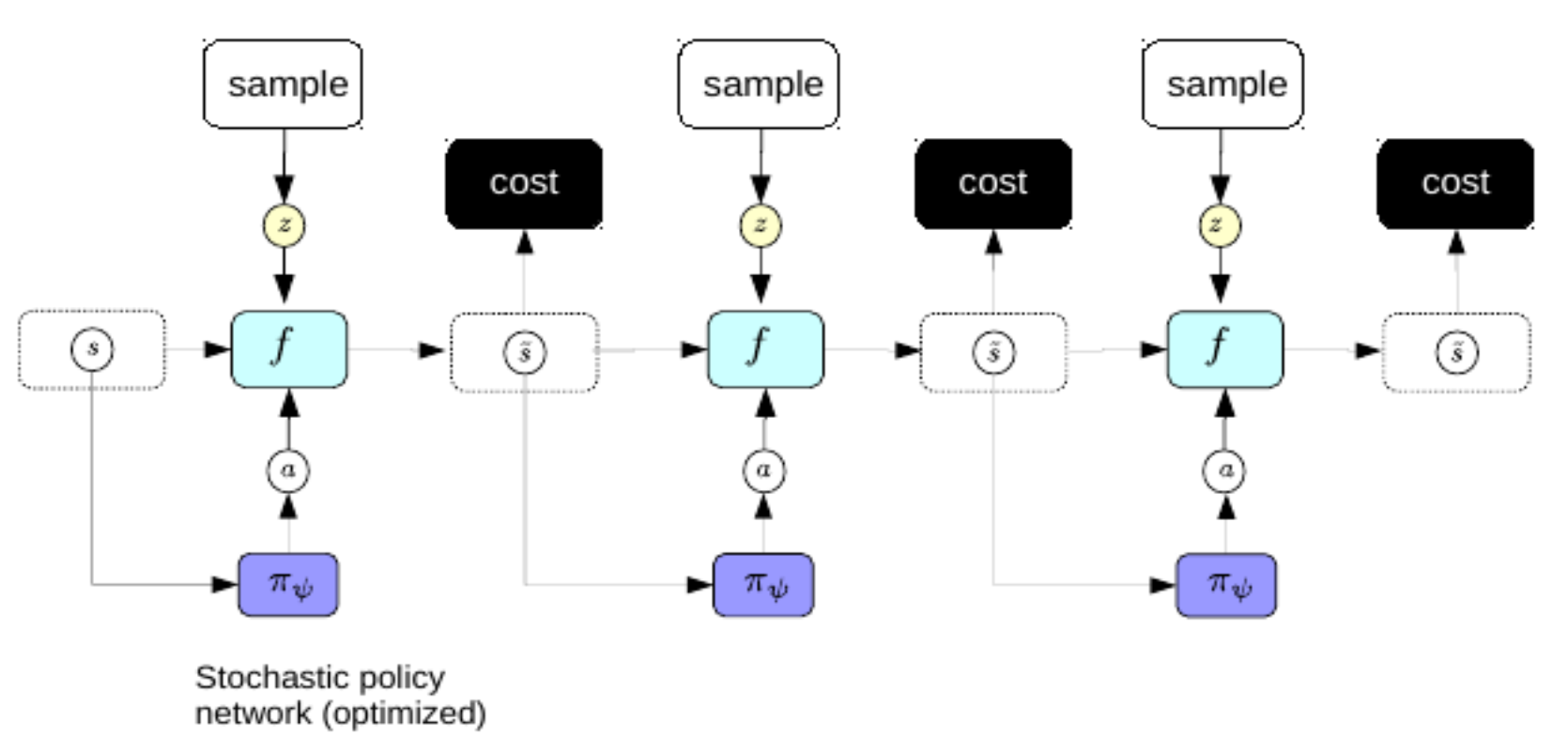
Fig. 3: Red de Políticas

Una vez entrenado, podemos usar la política de redes para predecir la secuencia óptima de acción inmediatamente después de la percepción

Aprendizaje Reforzado (RL)

Las principales diferencias entre RL y lo que hemos estudiado hasta este punto son dos:

1. En los entornos de aprendizaje por refuerzo, la función de costo es una caja negra. En otras palabras, el agente no comprende la dinámica de la recompensa.
2. En la configuración de RL, no utilizamos un modelo hacia adelante del mundo para avanzar en el ambiente. En cambio, interactuamos con el mundo real y aprendemos el resultado al observar lo que sucede. En el mundo real, nuestra medida del estado del mundo es imperfecta, por lo que no siempre es posible predecir lo que sucederá a continuación.

El principal problema del aprendizaje por refuerzo es que la función de costo no es diferenciable. Esto significa que la única forma de aprender es mediante prueba y error. Entonces el problema pasa a ser cómo explorar el espacio de estados de manera eficiente. Una vez que se le ocurre una solución a esto, el siguiente problema es la cuestión fundamental de exploración vs. explotación: ¿Preferiría tomar acciones para aprender al máximo sobre el ambiente o en su lugar explotar lo que ya ha aprendido para obtener una recompensa tan alta como sea posible?

Los métodos actor-crítico son una familia popular de algoritmos de RL que entrenan tanto a un actor como a un crítico. Muchos métodos de RL funcionan de manera similar, entrenando un modelo de la función de costo (el crítico). En los métodos actor-crítico, el papel del crítico es aprender el valor esperado de la función de valor. Esto permite la propagación hacia atrás a través del módulo, ya que el crítico es solo una red neuronal. La responsabilidad del actor es proponer acciones a tomar en el entorno, y el trabajo del crítico es aprender un modelo de la función de costos. El actor y el crítico trabajan en conjunto, lo que conduce a un aprendizaje más eficiente que si no se utiliza ningún crítico. Si no tienes un buen modelo del mundo, es mucho más difícil de aprender: Ej. El coche que está al lado del acantilado no sabrá que caer por un acantilado es una mala idea. Esto permite que los humanos y los animales aprendan mucho más rápido que los agentes de RL: tenemos modelos mundiales realmente buenos en nuestra cabeza.

No siempre podemos predecir el futuro del mundo debido a la incertidumbre inherente: incertidumbre aleatoria y epistémica. La incertidumbre aleatoria se debe a cosas que no se pueden controlar u observar en el entorno. La incertidumbre epistémica ocurre cuando no se puede predecir el futuro del mundo porque el modelo no tiene suficientes datos de entrenamiento.

A el modelo hacia delante le gustaría ser capaz de predecir

donde $z$ es una variable latente de la cuál no sabemos el valor. $z$ representa lo que no puedes saber sobre el mundo pero que aún influye en la predicción (es decir, incertidumbre aleatoria). Podemos regularizar $z$ con esparcidad, ruido, o con un codificador. Podemos usar modelos hacia adelante para aprender a planificar. El sistema trabaja al tener un decodificador decodificando una concatenación del estado de representación y la incertidumbre $z$. El mejor $z$ está definido como el $z$ que minimiza la diferencia entre $\hat s_{t+1}$ y el $s_{t+1}$ actual observado.

Red Generativa Adversaria (GAN)

Hay muchas variaciones de GAN y aquí pensamos en GAN como una forma de modelo basado en energía que utiliza métodos contrastivos. Empuja hacia arriba la energía de las muestras contrastivas y empuja hacia abajo la energía de las muestras de entrenamiento. Una GAN básica consta de dos partes: un generador que produce muestras contrastivas de manera inteligente y un discriminador (a veces llamado crítico) que es esencialmente una función de costo y actúa como un modelo energético. Tanto el generador como el discriminador son redes neuronales.

Los dos tipos de entrada a GAN son, respectivamente, muestras de entrenamiento y muestras contrastivas. Para las muestras de entrenamiento,la GAN pasa estas muestras a través del discriminador y hace que disminuya su energía. Para muestras contrastivas,la GAN muestrea variables latentes de alguna distribución, las pasa por el generador para producir algo similar a las muestras de entrenamiento y las pasa a través del discriminador para hacer que aumente su energía. La función de pérdida del discriminador es la siguiente:

Donde $L_d$ puede ser una función de pérdida basada en márgenes como $F(y) + [m - F(\bar{y})]^+$ or $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$ siempre y cuando haga disminuir a $F(y)$ e incremente $F(\bar{y})$. En éste contexto, $y$ es la etiqueta, y $\bar{y}$ es la variable de respuesta que proporciona la energía más baja, excepto a $y$ en sí.

donde $z$ es la variable latente y $G$ es la red neuronal generadora. Queremos hacer que el generador adapte su peso y produzca $\bar{y}$ con poca energía que pueda engañar al discriminador.

La razón por la que a este tipo de modelo se le llama red generativa adversaria es porque tenemos dos funciones objetivas que son incompatibles entre sí y necesitamos minimizarlas simultáneamente. No es un problema de descenso de gradiente porque el objetivo es encontrar un equilibrio de Nash entre estas dos funciones y el descenso de gradiente no es capaz de hacerlo de forma predeterminada.

Habrá problemas cuando tengamos muestras cercanas a la verdadera variedad. Suponga que tenemos una variedad infinitamente delgada. El discriminador necesita producir una probabilidad de $0$ fuera de la variedad y una probabilidad infinita en la variedad. Dado que esto es muy difícil de lograr, GAN usa sigmoide y produce $0$ fuera de la variedad y produce $1$ en la variedad. El problema con esto es que si entrenamos el sistema con éxito donde conseguimos que el discriminador produzca $0$ fuera de la variedad, la función de energía es completamente inútil. Esto se debe a que la función de energía no es uniforme donde toda la energía fuera de la variedad de datos será infinita y toda la energía en la variedad de datos será $0$. No queremos que el valor de la energía pase de $0$ al infinito en un paso muy pequeño. Los investigadores han propuesto muchas formas de solucionar este problema regularizando la función energética. Un buen ejemplo de GAN mejorado es Wasserstein GAN, que limita el tamaño del peso del discriminador.