Codificador automático disperso recurrente discriminativo y dispersión de grupos

Codificador automático disperso recurrente discriminativo (DrSAE)

La idea de DrSAE consiste en combinar codificación esparcida, o el codificador automático esparcido, con entrenamiento discriminativo

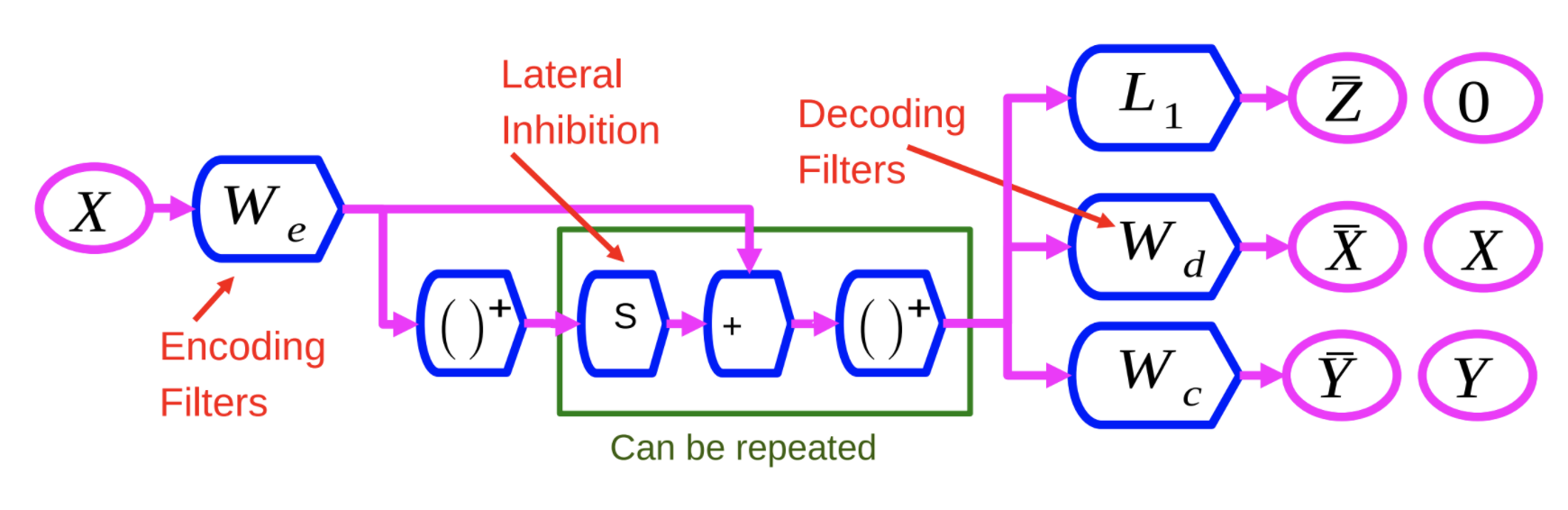
Fig 1: Red de codificador automático disperso recurrente discriminativo

El codificador, $W_e$, es similar al codificador en el método LISTA. La variable $X$ es atravesada por $W_e$ y luego por una no linealidad. Este resultado es luego multiplicado por otra matriz aprendida, $S$, y agregado a $W_e$. Posteriormente es enviado a través de otra no linealidad. Este proceso puede ser repetido un número de veces, con cada repetición como una capa.

Entrenamos la red neuronal con 3 criterios diferentes:

1. $L_1$: Aplicar el criterio $L_1$ en el vector de características $Z$ para hacerlo esparcido.
2. Reconstruir $X$: ésto se hace usando una matriz de decodificación que reproduce la entrada en la salida. Ésto se hace para minimizar el error cuadrático indicado por $W_d$ en la Figura 1.
3. Agregar un tercer término: Éste tercer término, indicado por $W_c$, es un simple clasificador lineal que intenta predecir una categoría.

El sistema es entrenado para minimizar los 3 criterios al mismo tiempo

La ventaja de ésto es que al forzar el sistema a encontrar representaciones que pueden reconstruir la entrada, implica que se está basicamente sesgando el sistema a extraer características que contienen tanta información acerca de la entrada como es posible. En otras palabras, enriquece las características.

Dispersión Grupal

La idea aquí es generar características dispersas, no solo características normales que son extraídas por convoluciones, sino basicamente producir características que son dispersas después del pooling

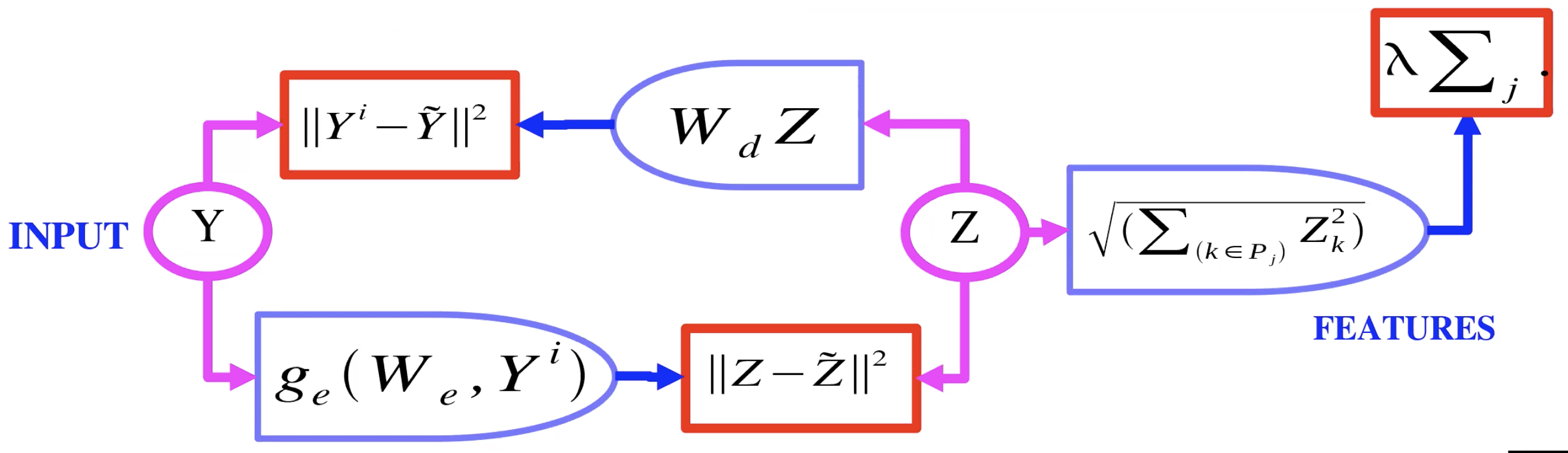
Fig 2: Codificador automático con dispersión de grupo

La Figura 2 muestra un ejemplo de un codificador automático con dispersión de grupo. Aquí, en lugar de que la variable latente $Z$ vaya a $L_1$, ella pasa por básicamente un $L_2$ sobre grupos. Entonces se puede tomar la norma $L_2$ para cada componente en un grupos de $Z$, y tomar la suma de esas normas. Ahora eso es lo que se usa como regularizador, esto implica que podemos tener la dispersión de grupos de $Z$. Éstos grupos, o pools de características, tienen a agrupar juntas características que son similares una con las otras.

Codificador automático (AE) con dispersión grupal: preguntas y aclaraciones

Q: ¿Puede una estrategia similar ser usada en la primera lámina con el regularizador siendo aplicado por el VAE?

A: Agregar ruido y forzar la dispersión en una VAE son dos maneras de reducir la información que tiene la variable latente/código. Evita el aprendizaje de una función de identidad

Q: En la lámina “AE con dispersión grupal”, ¿Qué es $P_j$?

A:$p$ es un pool de características. Para un vector $z$, sería el subconjunto de valores en $z$.

Q: Aclaración de pooling de características

A: (Yann dibuja una representación de AE con difusión grupal) El codificador produce la variable latente $z$, la cual es regularizada usando la norma $L_2$ de las características agrupadas. Éste $z$ es usado por el decodificador para la reconstrución de imagen.

Q: ¿La regularización grupal ayuda a agrupar características similares?

A: La respuesta no es clara, el trabajo realizado aquí se realizó antes de que la potencia / datos computacionales estuvieran fácilmente disponibles. Las técnicas no se han vuelto a poner en primer plano

Entrenamiento a nivel de imagen, filtros locales pero sin compartir peso

La respuesta sobre si ayuda o no, no está clara. Las personas interesadas en esto están interesadas en la restauración de imágenes o en algún tipo de aprendizaje auto supervisado. Esto funcionaría bien cuando el conjunto de datos fuera muy pequeño. Cuando se tiene un codificador y decodificador que es convolucional y se entrena con difusión grupal en celdas complejas, luego de que se termine de pre-entrenar, el sistema se deshace del decodificador y solo usa el codificador como extractor de características, digamos la primera capa de la red convolucional y se le añade una segunda capa encima.

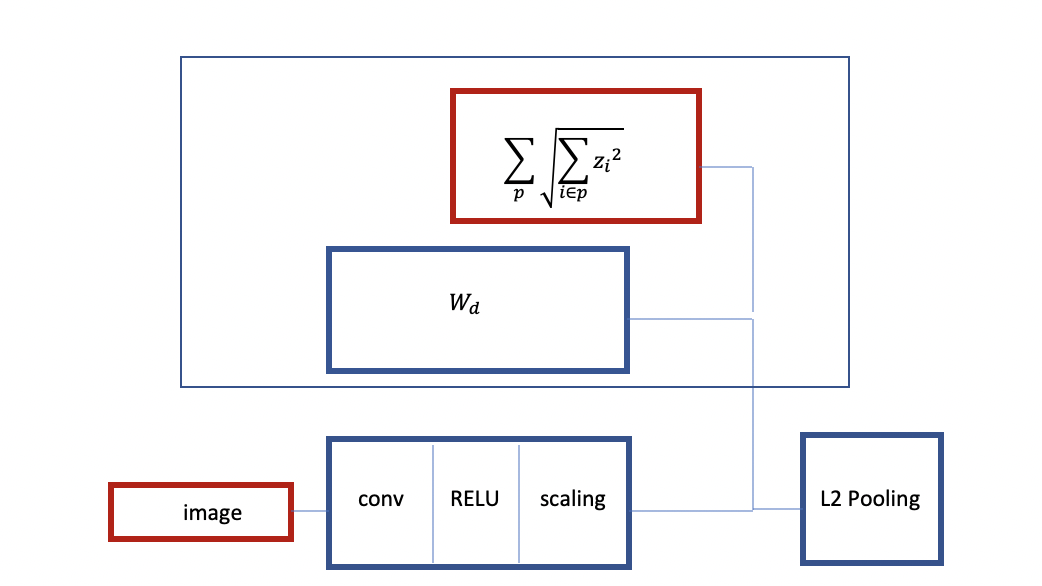
Fig 3: Estructura de una RELU Convolucional con difusión grupal

Como se puede ver arriba, se empieza con una imagen, se tiene un codificador el cuál es basicamente una RELU Convolucional y algún tipo de capa de escala después de este. Se entrena con difusión grupal. Se tiene un decodificador lineal y un criterio que es agrupar por 1. Se toma la difusión grupal como un regularizador. Ésto es como L2 pooling con una arquitectura similar a difusión grupal

También puedes entrenar otra instancia de ésta red. Ésta vez, puede agregar más capas y tener un decodificador con L2 pooling y criterio de difusión, entrenarlo para reconstruir su entrada con pooling arriba. Ésto va a crear una red convolucional pre-entrenada de 2 capas. Éste procedimiento es también llamado codificador automático apilado (Stacked Autoencoder). La característica principal aquí es que está entrenado para producir características invariantes con difusión grupal.

Q: ¿Deberíamos usar todos los posibles sub-árboles como grupos?

A: Eso depende de usted, puede usar múltiples árboles si quieres. Podemos entrenar el árbol con un árbol más grande de lo necesario y luego remover ramas que se usan raramente.

Fig 4: Entrenamiento a nivel de imagen, filtros locales pero no pesos compartidos

Estos son llamados patrones molinillo. Ésto es una especie de organización de las características. La orientación varia continuamente mientras recorres esos puntos rojos. Si tomamos uno de ésos puntos rojos y si hacemos un pequeño círculo alrededor de los puntos rojos, notarás que la orientación del extractor varía continuamente mientras te mueves. Tendencias similares son observadas en el cerebro.

Q : ¿Está el término de difusión grupal entrenado para tener un valor pequeño?

Éste es un regularizador. El término en sí mismo no es entrenado, es fijado. Éste es solo la norma L2 de los grupos y los grupos son predeterminados. Pero, como es un criterio, determina lo que hacen el codificador y decodificador y que clase de características van a ser extraídas.

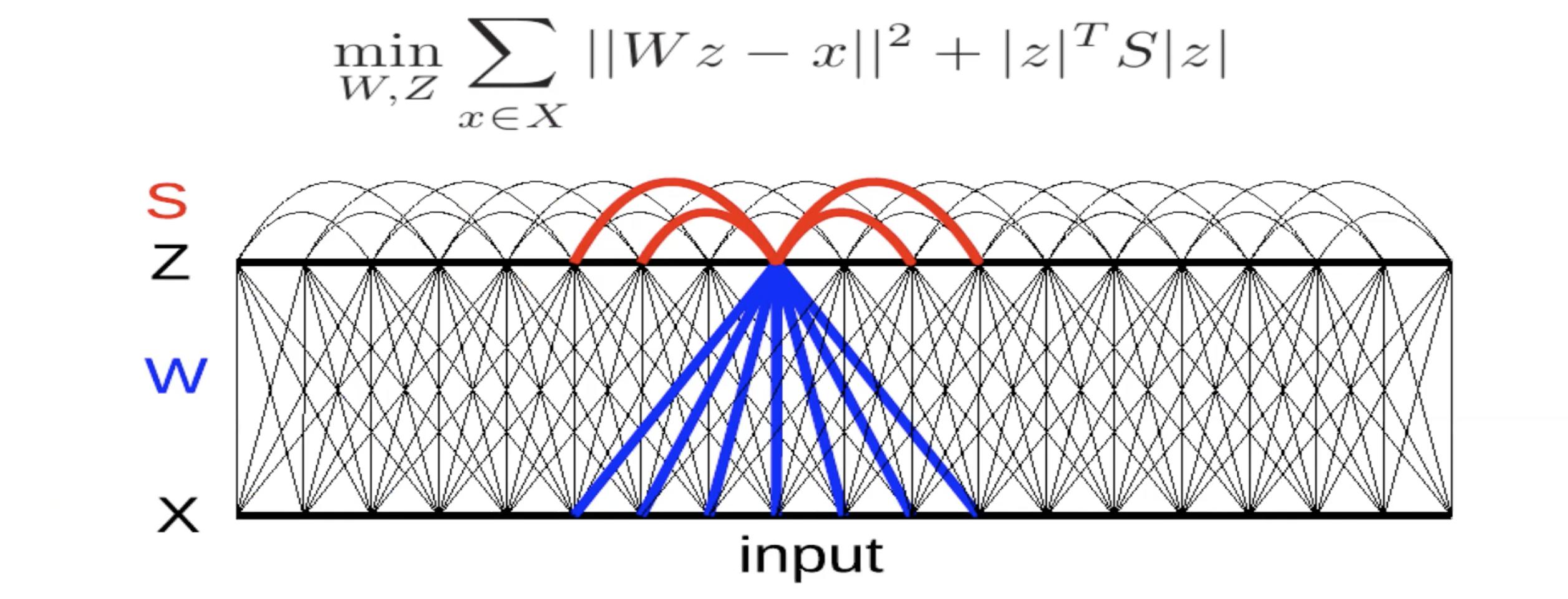
Fig 5: Características Invariantes a través de Inhibición Lateral.

Aquí, hay un decodificador lineal con error de reconstrución cuadrático. Hay un criterio en la energía. La matriz $S$ está determinada a mano o se aprende para maximizar éste término. Si los términos en $S$ son positivos y grandes, ello implica que el sistema no quiere $z_i$ y $z_j$ estén al mismo tiempos. En consecuencia, ésta especia de inhibición mutua (llamada inhibición natural en neurociencia). Así, estás intentando encontrar un valor para $S$ que es tan grande como es posible.

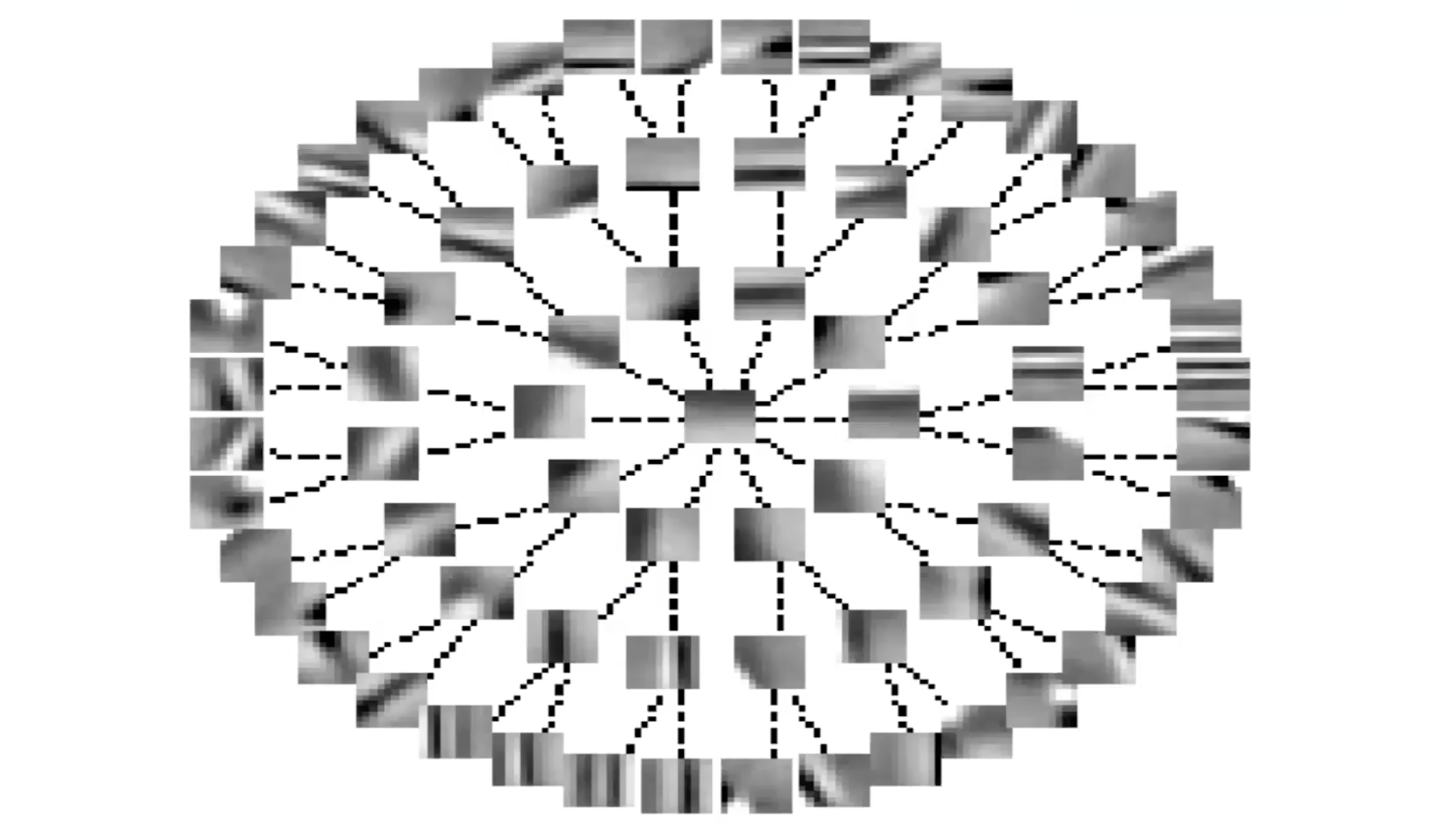
Fig 6: Características Invariantes a través de Inhibición Lateral (Forma de Árbol)

Si usted organiza S en términos de un árbol, las líneas representan los términos cero en la matriz $S$. Cuando usted no tiene una línea, existe un término no-cero. Entonces, cada característica inhibe todas las otras características exceptuando aquellas que están arriba del árbol o abajo del árbol de él. Ésto es algo así como lo opuesto a la difusión grupal.

Verá nuevamente que los sistemas están organizando características de una manera más o menos continua. Las características a lo largo de la rama de un árbol representan la misma característica con diferentes niveles de selectividad. Las características a lo largo de la periferia varían de forma más o menos continua porque no hay inhibición.

Para entrenar éste sistema, en cada iteración, usted da un $x$ y encuentra la $z$ que minimiza ésta función de energía. Luego da un paso de descenso de gradiente para actualizar $W$. También puedes hacer un paso de ascenso de gradiente para hacer los términos en $S$ más grandes.