Modelos Generativos - Auto-encodificadores Variacionales

Recapitulación: Auto-encodificador ^Auto-encoder(AE)

En resumen, a alto nivel, en una forma muy simple un AE es de la siguiente manera:

• Primero, el auto-encodificador^auto-encoder toma una entrada y la hace corresponder con un estado oculto a través de una transformación afín $\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$, donde $f$ es una función de activación (entre elementos). Esta es la etapa de encodificación. Note que $\boldsymbol{h}$ es también llamado el código.
• Después, $\hat{\boldsymbol{x}} = g(\boldsymbol{W}x \boldsymbol{h} + \boldsymbol{b}x)$, donde $g$ es una función de activación. Esta es la etapa de decodificación.

Para una explicación detallada, consulte las notas de la Semana 7.

Intuición atrás de VAE y una comparación con los auto-encodificadores clásicos

Presentamos los Auto-encodificadores Variacionales (VAE), un tipo de modelos generativos. Pero, ¿por qué debemos interesarnos sobre modelos generativos? Para responder esta pregunta, los modelos discriminativos aprenden a realizar predicciones dadas algunas observaciones, pero los modelos generativos apuntan a simular el proceso de generación de datos. En consecuencia, los modelos generativos pueden entender mejor las relaciones casuales subyacentes que llevan a una mejor generalización.

Note que, aunque VAE tiene “Auto-encodificadores” (AE) en su nombre (debido a la similitud estructural a los auto-encodificadores), las formulaciones entre VAEs y AEs son muy diferentes. Ver la Figura 1 abajo.

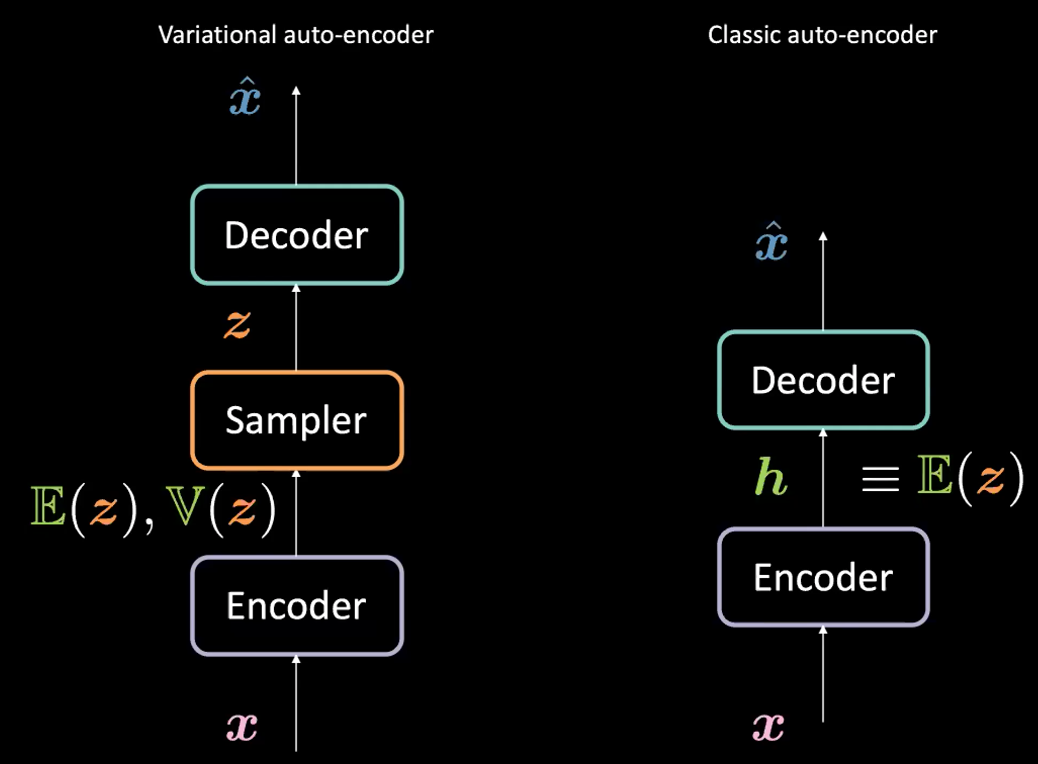
Fig. 1: VAE *vs.* AE Clásico.

¿Cuál es la diferencia entre un auto-encodificador variacional (VAE) y un auto-encodificador clásico (AE)?

Para VAE:

• Primero, la etapa de encodificación: pasamos la entrada $\boldsymbol{x}$ al encodificador. En lugar de generar una representación oculta $\boldsymbol{h}$ (the code) en el AE, el código en el Auto-encodifcador variacional (VAE) está formado por dos cosas: $\mathbb{E}(\boldsymbol{z})$ y $\mathbb{V}(\boldsymbol{z})$ donde $\boldsymbol{z}$ es la variable aleatoria latente que sigue una distribución Gaussiana con media $\mathbb{E}(\boldsymbol{z})$ y varianza $\mathbb{V}(\boldsymbol{z})$. Note que las personas en la práctica utilizan distribuciones Gaussianas como la distribución encodificada, pero otras distribuciones también pueden ser utilizadas.
  • El encodificador será una función de $\mathcal{X}$ a $\mathbb{R}^{2d}$: $\boldsymbol{x} \mapsto \boldsymbol{h}$ (aquí usamos $\boldsymbol{h}$ para representar la concatenación de $\mathbb{E}(\boldsymbol{z})$ y $\mathbb{V}(\boldsymbol{z})$).
• Después, muestreamos $\boldsymbol{z}$ de la distribución anterior parametrizada por el encodificador; específicamente, $\mathbb{E}(\boldsymbol{z})$ y $\mathbb{V}(\boldsymbol{z})$ son pasados dentro de un muestrador para generar la variable latente $\boldsymbol{z}$.
• Después, $\boldsymbol{z}$ es pasado en el decodificador para generar $\hat{\boldsymbol{x}}$.
  • El decodificador será una función de $\mathcal{Z}$ hacia $\mathbb{R}^{n}$: $\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$.

En realidad, para el auto-encodificador clásico, podemos pensar en $\boldsymbol{h}$ justamente como el vector $\E(\boldsymbol{z})$ en la formulación de auto-codificador variacional VAE. En resumen, la principal diferencia entre VAEs y AEs es que los VAEs tienen un buen espacio latente que hace posible un proceso generativo.

La función objetivo(perdida) de un VAE

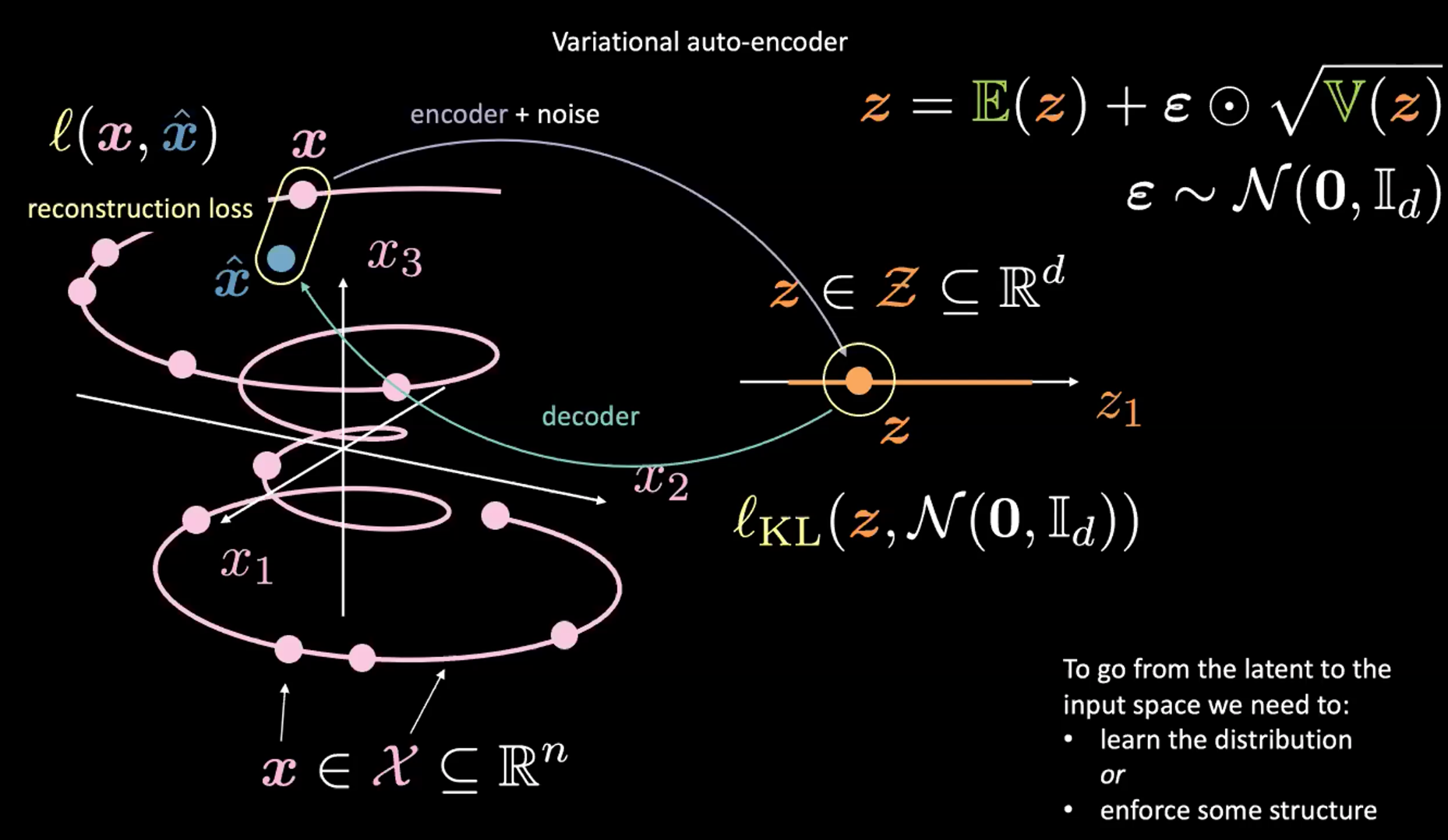
Fig. 2: Mapeo del espacio de entrada a un espacio latente.

Observe la Figura 2 arriba. Por ahora, ignore la esquina superior derecha (la cual es el truco de re-parametrización explicado en la sección siguiente).

Primero, encodificamos desde el espacio de entrada(izquierda) hacia el espacio latente(derecha), a través del encodificador y ruido. Siguiente, decodificamos desde el espacio latente (derecha) hacia el espacio de salida (izquierda). Para ir desde el espacio latente hacia el espacio de entrada (el proceso generativo) necesitamos ya sea aprender la distribución (del código latente) o reforzar alguna estructura. En nuestro caso, VAE refuerza alguna estructura al espacio latente.

Como es usual, para entrenar un VAE, minimizamos una función de perdida. Por lo tanto, La función de perdida está compuesta por un término de reconstrucción y también un término de regularización.

• El término de reconstrucción está en la capa final (lado izquierdo de la figura). Esto corresponde a $l(\boldsymbol{x}, \hat{\boldsymbol{x}})$ en la figura.
• El término de regularización está en la capa latente, para reforzar alguna estructura Gaussiana especifica en el espacio latente (lado derecho de la figura). Hacemos esto utilizando un término de penalización $l{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}d))$. Sin este término, un VAE actuara como un auto-encodificador clásico, lo cual puede llevar a sobreajuste y no tendremos las propiedades generativas que nosotros deseamos.

Discusión sobre el muestreo de $\boldsymbol{z}$ (truco de re-parametrización)

¿Como muestreamos de la distribución entregada por el encodificador en un VAE? De acuerdo a lo anterior, nosotros muestreamos desde la distribución Gaussiana, para obtener $\boldsymbol{z}$. Sin embargo, esto es problemático, debido a que cuando realizamos el algoritmo de gradiente descendiente para entrenar el modelo VAE, no sabemos cómo realizar retro-propagación a través del módulo de muestreo.

En lugar de eso, utilizamos el truco de re-parametrización para “muestrear” $\boldsymbol{z}$. Utilizamos $\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$ donde $\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$. En este caso, la retro-propagación en el entrenamiento es posible. Específicamente, las gradientes pasaran a través de la multiplicación y adición (entre elementos) en la ecuación de arriba.

Descomposición de la función de pérdida de un VAE

Visualizando estimaciones de la variable latente y pérdida de reconstrucción

Como se indicó anteriormente, la función de perdida para un VAE contiene dos partes: un término de reconstrucción y un término de regularización. Podemos escribir eso como:

Para visualizar el propósito de cada termino en la función de perdida, podemos pensar en cada valor estimado $\boldsymbol{z}$ como un círculo en un espacio $2d$, donde el centro del circulo es $\mathbb{E}(\boldsymbol{z})$ y el área alrededor son los posibles valores de $\boldsymbol{z}$ determinados por $\mathbb{V}(\boldsymbol{z}).$

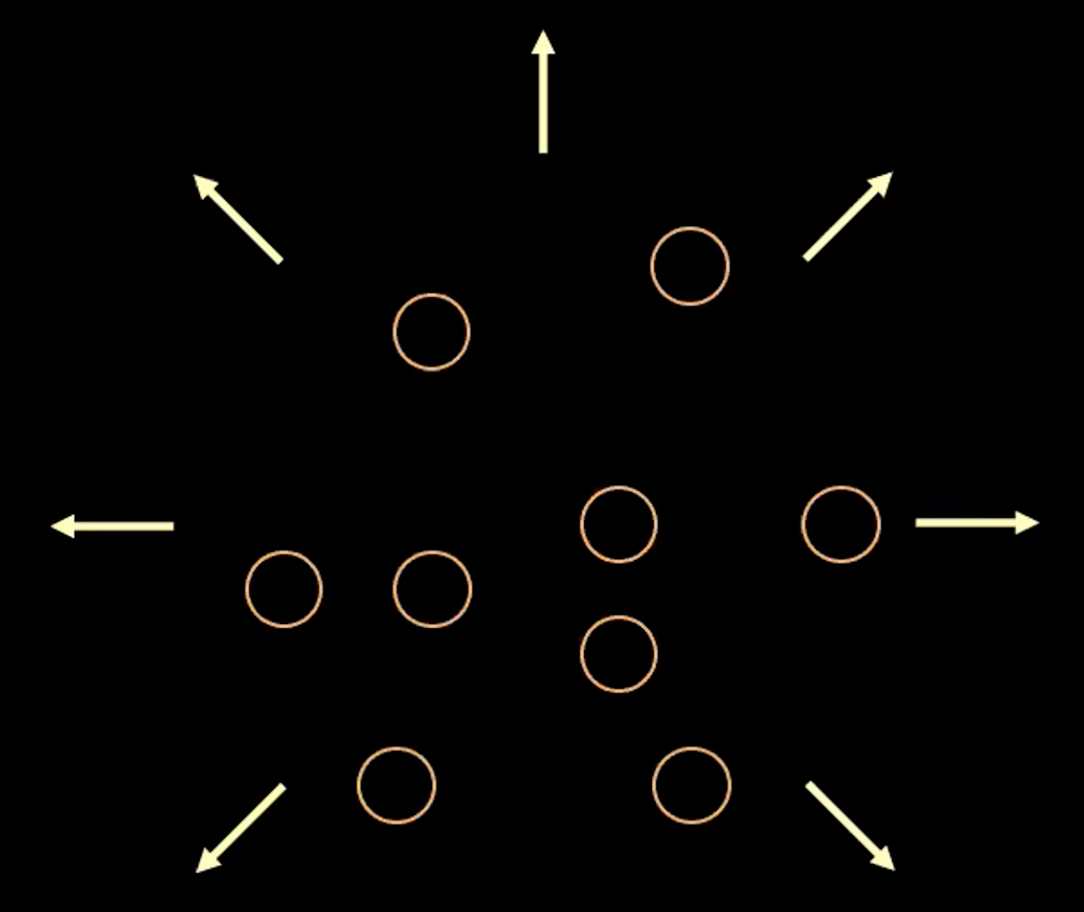
Fig. 3: Visualizando el vector $z$ como burbujas en el espacio latente.

En la Figura 3 de arriba, cada burbuja representa una región estimada de $\boldsymbol{z}$, y las flechas representan como el termino de reconstrucción empuja lejos de los otros cada valor estimado, lo cual es explicado más adelante.

Si hay un traslape entre dos estimados cualquiera de $z$, (visualmente, si dos burbujas se traslapan) esto crea ambigüedad para la reconstrucción debido a que ambos puntos en el traslape pueden ser mapeados a la misma entrada original. Por lo tanto, la pérdida de reconstrucción empujara los puntos lejos uno de otro.

Sin embargo, si utilizamos solamente la pérdida de reconstrucción, los estimados continuarán siendo empujados lejos uno de otro y el sistema podría explotar. Aquí es donde el termino de penalización entra en juego.

Nota: Para entradas binarias la pérdida de reconstrucción es:

Y para entradas de valores reales la pérdida de reconstrucción es:

El término de penalización

El segundo término es la entropía relativa (una medida de distancia entre dos distribuciones) entre $\boldsymbol{z}$ la cual viene de una distribución Gaussiana con media $\mathbb{E}(\boldsymbol{z})$, varianza $\mathbb{V}(\boldsymbol{z})$ y la distribución normal estándar. Si expandimos este segundo término en la función de pérdida del VAE obtenemos:

Donde cada expresión en la sumatoria tiene cuatro términos. Abajo en la Figura 4 escribimos y graficamos los primeros tres términos.

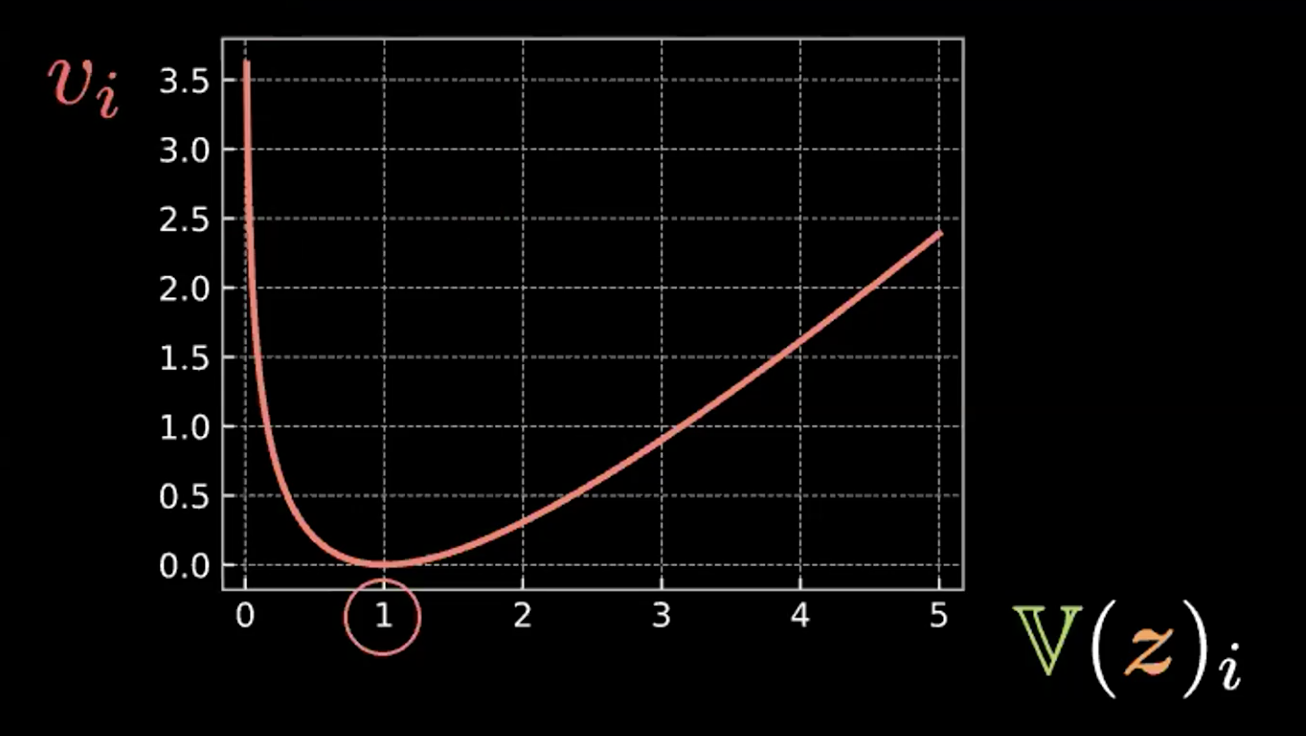
Fig. 4: Gráfico mostrando como la entropía relativa fuerza a las burbujas para tener una varianza = 1.

Así podemos ver que esta expresión es minimizada cuando $z_i$ tiene varianza 1. Por lo tanto, nuestra pérdida de penalización mantendrá la varianza de nuestras variables latentes estimadas cerca de 1. Visualmente, esto significa que nuestras “burbujas” de arriba tendrán un radio cercano a 1.

El ultimo término, $\mathbb{E}(z_i)^2$, minimiza la distancia entre $z_i$ y por lo tanto previene la “explosión” impulsada por el término de reconstrucción.

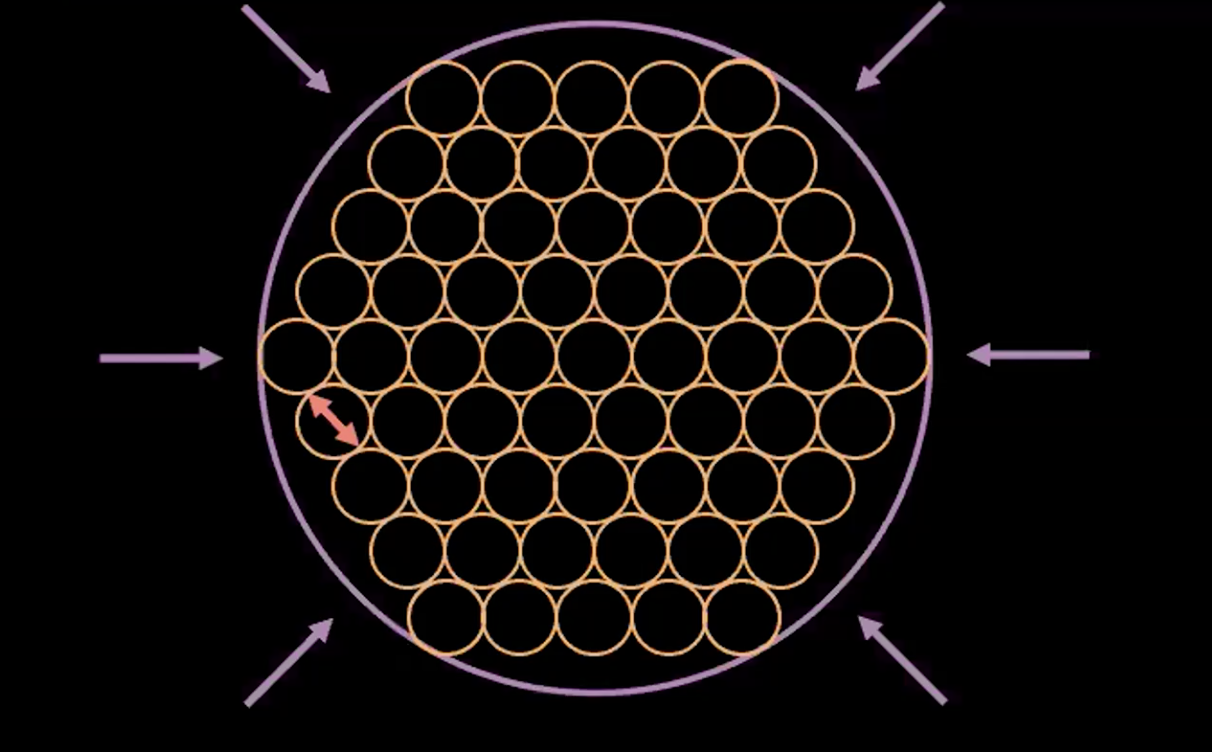
Fig. 5: La interpretación "burbuja-de-burbujas" de un VAE

La figura 5 de arriba muestra como la pérdida de un VAE empuja las variables latentes estimadas lo más cercano posible sin algún traslape, manteniendo así la varianza estimada de cada punto cerca a uno.

Nota: El $\beta$ en la función de pérdida del VAE es un hiper-parámetro que dicta como ponderar los términos de penalización y reconstrucción.

Implementación de un Auto-encodificador Variacional (VAE)

El Jupyter Notebook puede ser encontrado aquí.

En este Jupyter Notebook, implementamos un VAE y lo entrenamos en el conjunto de datos MNIST. Después muestreamos $\boldsymbol{z}$ de una distribución normal y alimentamos el decodificador y comparamos el resultado. Finalmente, observamos como cambia $\boldsymbol{z}$ en una proyección 2D.

Nota: En el conjunto de datos usado MNIST, los valores de los píxeles fueron normalizados para estar en el rango de $[0, 1]$.

El Encodificador y el Decodificador

1. Definimos el encodificador y el decodificador en nuestro módulo VAE.
2. Para la última capa lineal del encodificador, definimos el tamaño de la salida para que sea $2d$, de la cual los primeros valores $d$ son las medias y valores los restantes $d$ son las varianzas. Muestreamos $\boldsymbol{z} \in R^d$ usando estas medias y varianzas como fue explicado anteriormente en el truco de re-parametrización.
3. Para la última capa lineal en el decodificador, utilizamos la activación sigmoide para que podamos tener una salida en el rango $[0, 1]$, similar a los datos de entrada.

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

Re-parametrización y la función hacia adelante ^foward

Para la función reparametrise, si el modelo está en modo de entrenamiento, calculamos la desviación estándar (std) del logaritmo de la varianza (logvar). Utilizamos el logaritmo de la varianza en lugar de la varianza porque queremos asegurarnos que la varianza es no-negativa, y tomar el logaritmo de ella nos asegura que obtendremos el rango completo de la varianza, lo cual hace que el entrenamiento sea más estable.

Durante el entrenamiento, la función reparametrise realizará el truco de re-parametrización para que podamos realizar la retro-progragación en el entrenamiento. Para conectar con el concepto de una burbuja amarilla, como fue explicado en la lección, cada vez que esta función es llamada, dibujamos un punto eps = std.data.new(std.size()).normal_(), si realizamos esto 100 veces, obtendremos 100 puntos los cuales aproximadamente forman una esfera debido a que es una distribución normal, y la línea eps.mul(std).add_(mu) formará esta esfera centrada en mu con un radio igual a std.

Para la función forward, primero calculamos mu, (primera mitad) y logvar (segunda mitad) obtenidas del encodificador, después calculamos $\boldsymbol{z}$ por medio de la función reparamterise. Finalmente, devolvemos la salida del decodificador.

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        eps = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

Función de pérdida para el VAE

Aquí definimos la reconstrucción de perdida (entropía cruzada binaria ^{binary cross entropy} y la entropía relativa (penalización de divergencia KL).

def loss_function(x_hat, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + KLD

Generando nuevas muestras

Después de entrenar nuestro modelo, podemos muestrear un $z$ aleatorio desde la distribución normal y alimentar nuestro decodificador con él. Podemos observar en la Figura 6 que algunos de los resultados no son buenos debido a que nuestro decodificador no ha “cubierto” el espacio latente completamente. Esto puede ser mejorado si entrenamos el modelo por más épocas.

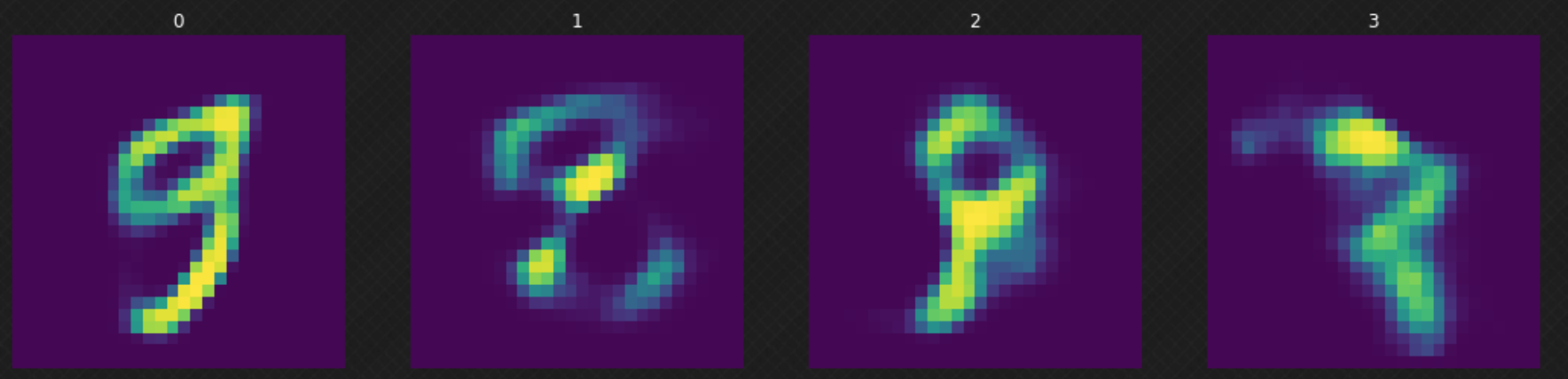
Fig. 6: Moviéndose aleatoriamente en el espacio latente.

Podemos ver como un dígito se transforma en otro, lo cual no sería posible si hubiéramos utilizado un auto-encodificador. Podemos ver que cuando caminamos en el espacio latente, la salida del decodificador aun parece legitima. La Figura 7 de abajo muestra como transformamos el dígito $3$ a $8$.

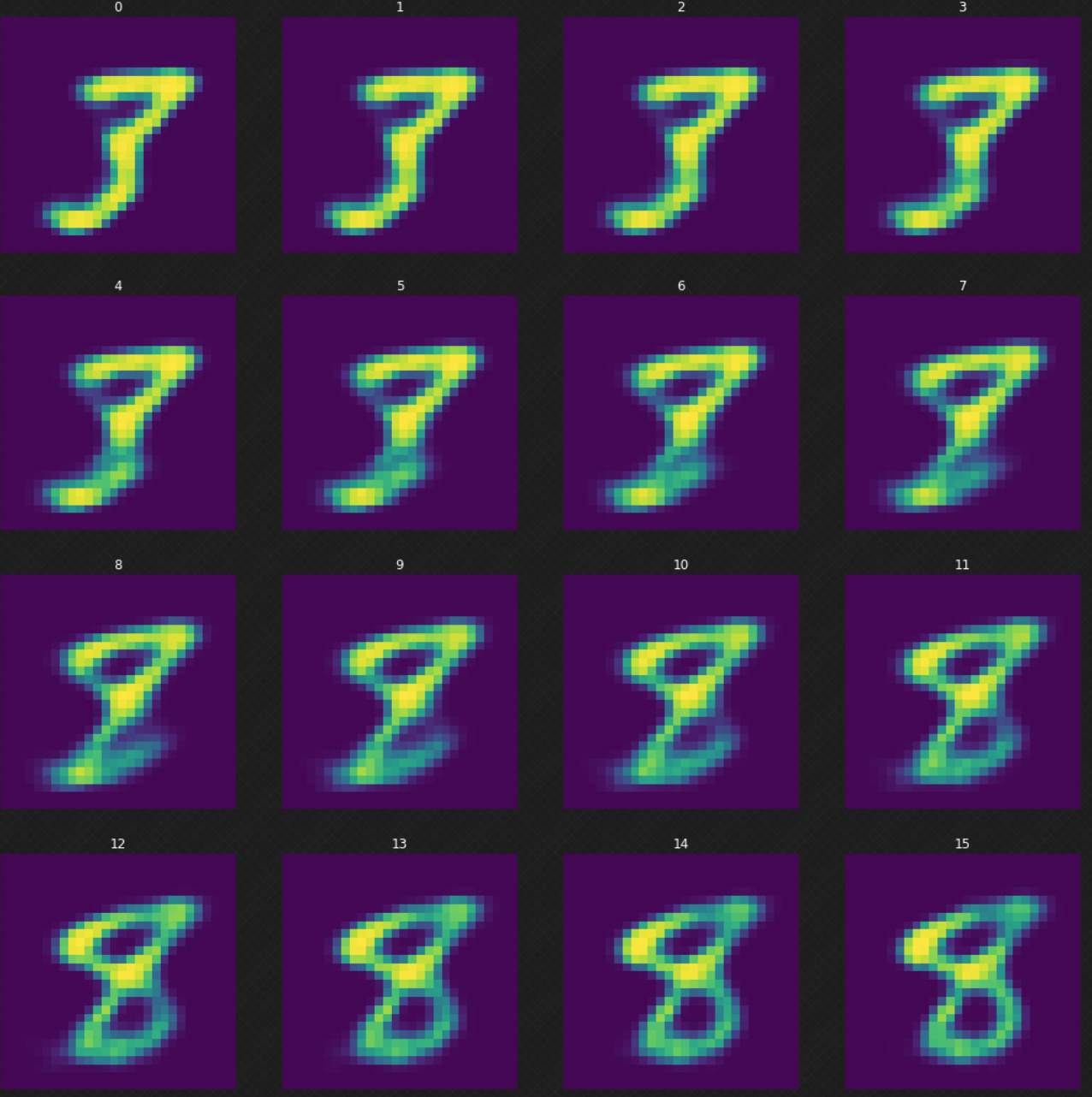
Fig. 7: Transformando el dígito 3 en 8.

Proyección de medias

Finalmente, echemos un vistazo a como el espacio latente cambia durante/después del entrenamiento. Los siguientes gráficos en la Figura 8 son las medias de la salida del encodificador, proyectadas en un espacio 2D, donde cada color representa un dígito. Podemos ver que en la época 0, las clases están dispersas en todos lados, solamente con una pequeña concentración. Conforme el modelo es entrenado, el espacio latente se vuelve mejor definido y las clases(dígitos) inician a formar grupos.

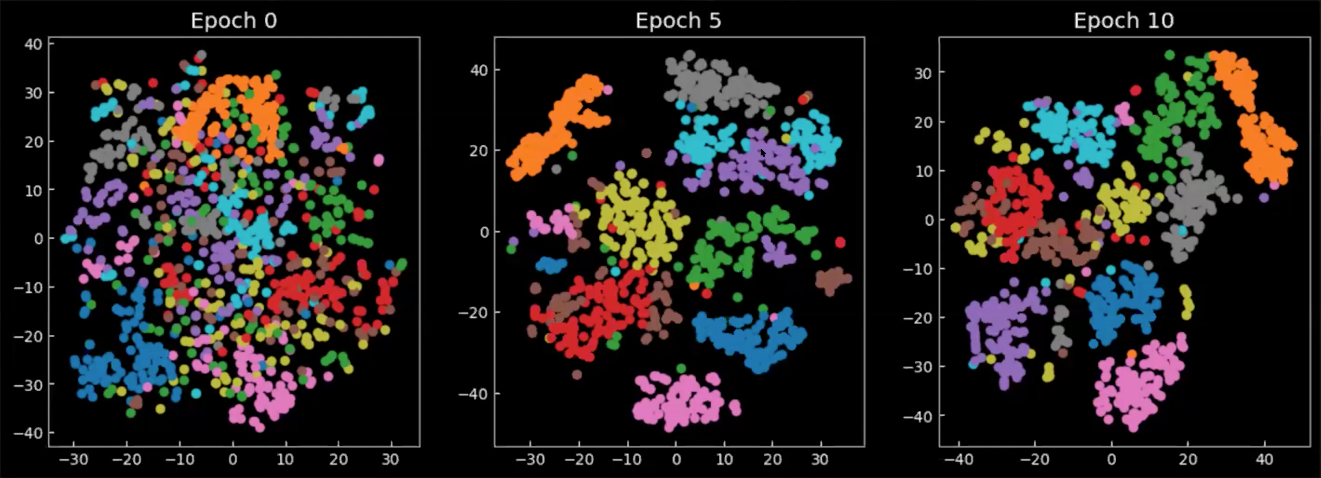
Fig. 8: Proyección 2D de las medias $\E(\vect{z})$ en el espacio latente.