Modelos basados en energía de variables latentes regularizadas

Modelos basados en energía de variables latentes regularizadas.

Los modelos con variables latentes son capaces de hacer una distribución de predicciones $\overline{y}$ condicionadas en una entrada observada $x$ y una variable latente adicional $z$. Los modelos basados en energía pueden también contener variables latentes:

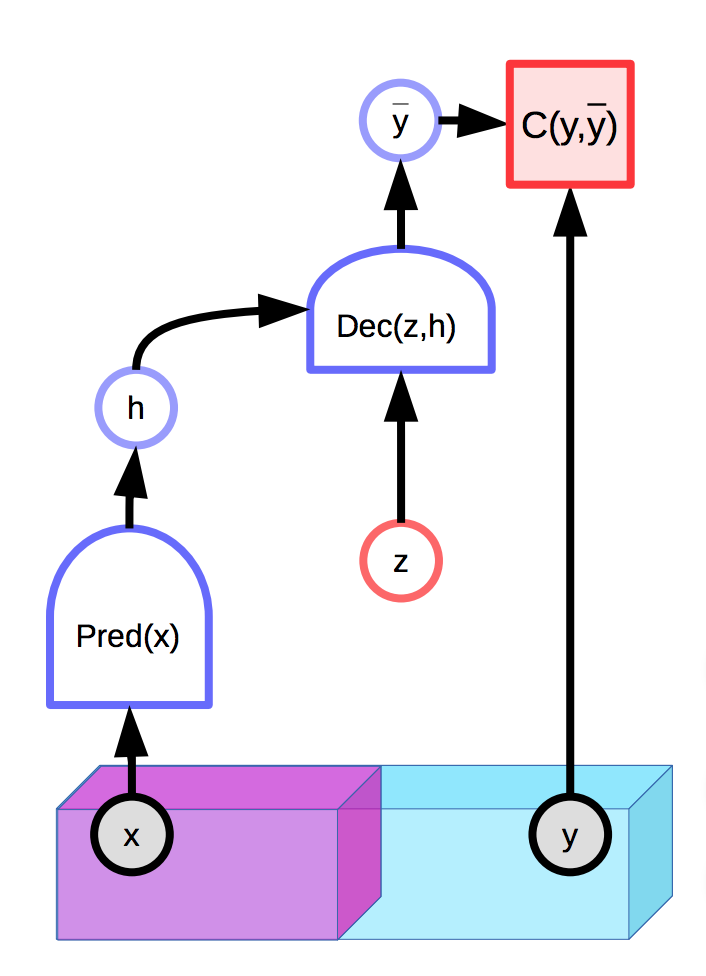
Fig. 1: Ejemplo de un EBM (modelo basado en energía) con una variable latente.

Ver notas de lecciones pasadas para más detalles

Desafortunadamente, si la variable latente $z$ tiene mucho poder expresivo en producir una predicción final $\overline{y}$, cada salida verdadera $y$ va a ser perferctamente reconstruida desde la entrada $x$ con una $z$ apropiadamente elegida. Esto significa que la función de energía será 0 en todas partes, ya que la energía es optimizada sobre ambas $y$ y $z$ durante inferencia.

Una solución natural es limitar la capacidad de información de la variable latente $z$. Una forma de hacer esto es regularizar la variable latente

Este método va a limitar el volumen de espacio de $z$ que toma un valor pequeño y el valor que, a su vez, controlará el espacio de $y$ que tiene energía baja. El valor de $\lambda$ controla esta compensación. Un ejemplo útil de $R$ es la norma $L_1$, que a su vez puede ser vista como una aproximación diferenciable de dimension efectiva en casi todas partes. Agregar ruido a $z$ mientras se limita su norma $L_2$ puede también limitar el contenido de su información (VAE).

Codificación esparcida (Sparse Coding)

La codificación esparcida es un ejemplo de un EBM (modelo basado en energía) de variable latente regularizada el cual esencialmente intenta aproximar los datos con una función lineal a trozos

El vector $n$-dimensional va a tender a tener un máximo número de componentes no-cero $m « n$. Luego cada $Wz$ será de elementos en la extensión de $m$ columnas de $W$

Luego de cada paso de optimización, la matriz $W$ y la variable latente $z$ son normalizadas por la suma de las normas $L_2$ de las columnas de $W$. Ésto asegura que $W$ y $z$ no diverjan al infinito y cero.

FISTA

Fig. 2: Grafo computacional FISTA

FISTA (ISTA rápido, por sus siglas en inglés) es un algoritmo que optimiza la función de energía de la codificación esparcida $E(y,z)$ con respecto a $z$ a través de alternadamente optimizar los dos términos $\Vert y - Wz\Vert^2$ y $\lambda \Vert z\Vert_{L^1}$. Inicializamos $Z(0)$ e iterativamente actualizamos $Z$ de acuerdo con la siguiente regla:

La expresión interna $Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$ es un paso de gradiente por el término $\Vert y - Wz\Vert^2$. La función $\text{Shrinkage}$ cambia los valores hacia 0, lo cual optimiza el término $\lambda \Vert z\Vert_{L_1}$.

LISTA

FISTA es muy costoso para ser aplicado en conjuntos largos de data de alta dimensión (e.j. imágenes). Una manera de hacerlo más eficiente es entrenar una red para predecir el valor óptimo de la variable latente $z$:

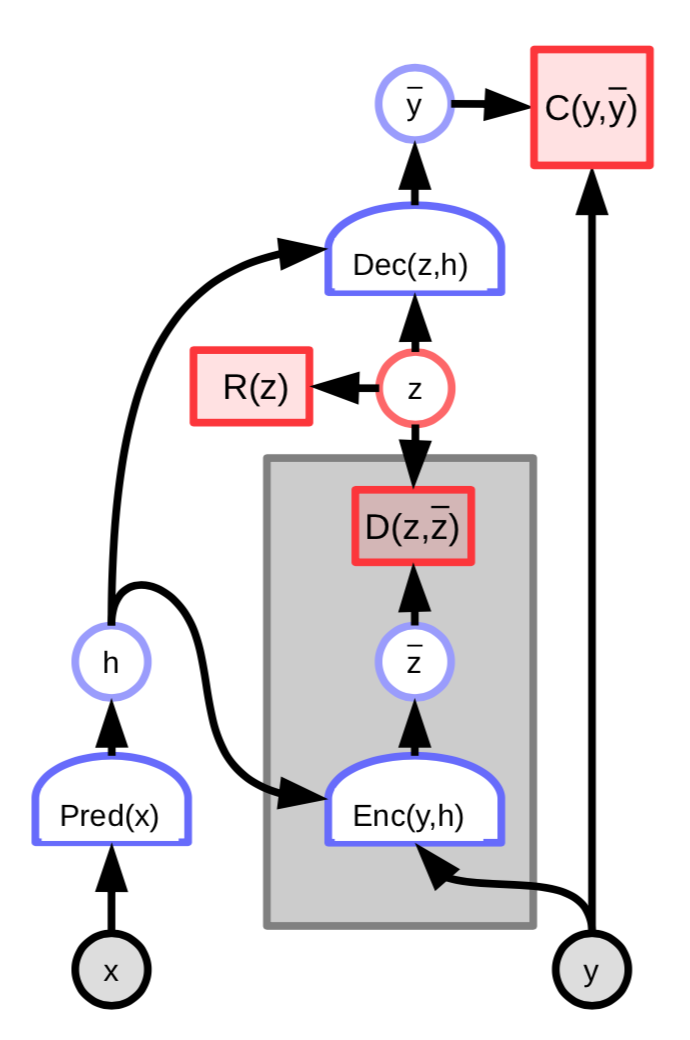
Fig. 3: EBM (Modelo basado en energía) con un codificador de variable latente

La energía de ésta arquitectura incluye un término adicional que mide la diferencia entre la variable latente predecida $\overline z$ y la variable latente óptima $z$:

Podemos definir aún más

y luego escribir

Ésta regla de actualización puede ser interpretada como una red recurrente, lo que sugiere que en su lugar podemos aprender los parámetros $W_e$ que iterativamente determinan la variable latente $z$. La red es manejada por un número fijo de pasos de tiempo $K$ y los gradientes de $W_e$ se computan usando la estándar propagación hacia atrás a través del tiempo. La red entrenada luego produce un buen $z$ en menos iteraciones que el algoritmo FISTA.

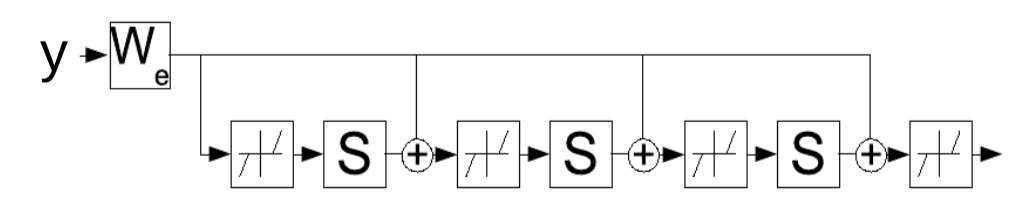
Fig. 4: LISTA como una red recurrente desplegada a través del tiempo

Ejemplos de codificación esparcida

Cuando un sistema de codificación esparcida con vectores latentes de 256 dimensiones es aplicado a los números escritos a mano MNIST, el sistema aprende un conjunto de 256 trazos que pueden ser linearmente combinados para reproducir casi todo el conjunto de entrenamiento. El regularizador de esparcimiento asegura que puedan ser reproducidos desde un número de trazos pequeño.

Fig. 5: Codificación esparcida en MNIST. Cada imagen es una columna aprendida de $W$.

Cuando un sistema de codificación esparcido es entrenado en parches de imágenes naturales, las características (features) aprendidas son filtros Gabor, que tienen bordes orientados. Éstas caracteristicas aprenddidas se asemejan a las aprendidas en las primeras partes de los sistemas visuales animales.

Codificación esparcida convolucional

Supongamos que tenemos una imagen y los mapas de características (feature maps, $z_1, z_2, \cdots, z_n$) de la imagen. Entonces podemos convolucionar ($*$) cada uno de los mapas de características con el kernel $K_i$. Luego la reconstrucción puede ser simplemente calculada como:

Ésto es diferente de la codificación esparcida original donde la reconstrucción fue hecha como $Y=\sum_{i}W_iZ_i$. En la codificación esparcida regular, tenemos una suma ponderada de columnas donde los pesos son coeficientes de $Z_i$. En la codificación convolucional esparcida, esto es todavía una operación lineal pero el diccionario matriz es ahora un conjunto de mapas de características que pueden convolucionar cada mapa de característica con cada kernel y sumar los resultados.

Auto-codificador convolucional esparcido en imágenes natirales

Fig.6 Fitros y funciones Bases obtenidas. Decodificador lineal convolucional

Los fitros en el codificador y decodificador lucen muy similares. El codificador es simplemente una convolución seguida de alguna no-linealidad y luego una capa diagonal para cambiar la escala. Luego hay escasez en las restricciones del código. El decodificador es solo un decodificador convolucional lineal y la reconstrucción aquí es el error cuadrático.

Entonces, si imponemos que hay un solo filtro entonces entonces es solo un filtro de tipo envolvente central. Con dos filtros, podemos obtener algunos filtros de formas extrañas. Con cuatro filtros, obtenemos bordes orientados (horizontales y verticales); obtenemos 2 polaridades para cada uno de los filtros. Con ocho filtros podemos obtener bordes orientados en ocho direcciones diferentes. Con 16, obtenemos más orientación junto con los centros alrededor. Mientras vamos incrementando los filtros, obtenemos filtros más diversos además de los detectores de bordes, también obtenemos detectores de rejilla de varias orientaciones, centros alrededor, etc.

Éste fenómeno parece ser interesante ya que es similar a lo que observamos en la corteza visual. Entonces ésto es una indicación de que podemos aprender buenas características (features) en un modo completamente no supervisado.

Como uso secundario, si tomamos estas características y las conectamos en una red convolucional y luego la entrenamos en alguna tarea, no necesariamente tendremos mejores resultados que entrenar una red de imágenes desde cero. Sin embargo, existen algunas instancias donde puede ayudar a impulsar el rendimiento. Por ejemplo, en casos donde el número de ejemplos no es lo suficientemente largo o hay pocas categorías, al entrenarlo en una manera puramente supervisada, obtenemos características degeneradas

Fig. 7 Codificación convolucional esparcida en una imagen a color

La figura anterior es otro ejemplo de imágenes a color. El kernel codificador (del lado derecho) es de tamaño 9 por 9. Éste kernel es aplicado convolucionalmente sobre toda la imagen. La imagen a la izquierda es de los códigos esparcidos del codificador. El vector $Z$ es un espacio muy esparcido donde existen sólo unos pocos componentes que son blanco o negro (no gris).

Auto-codificador variable (Varational autoencoder)

Los auto-codificadores variables tienen una arquitectura similar a los EBM de variables latentes regularizadas, con la excepción del esparcimiento. Por lo contrario, la información contenida del código es limitada al hacerlo ruidoso.

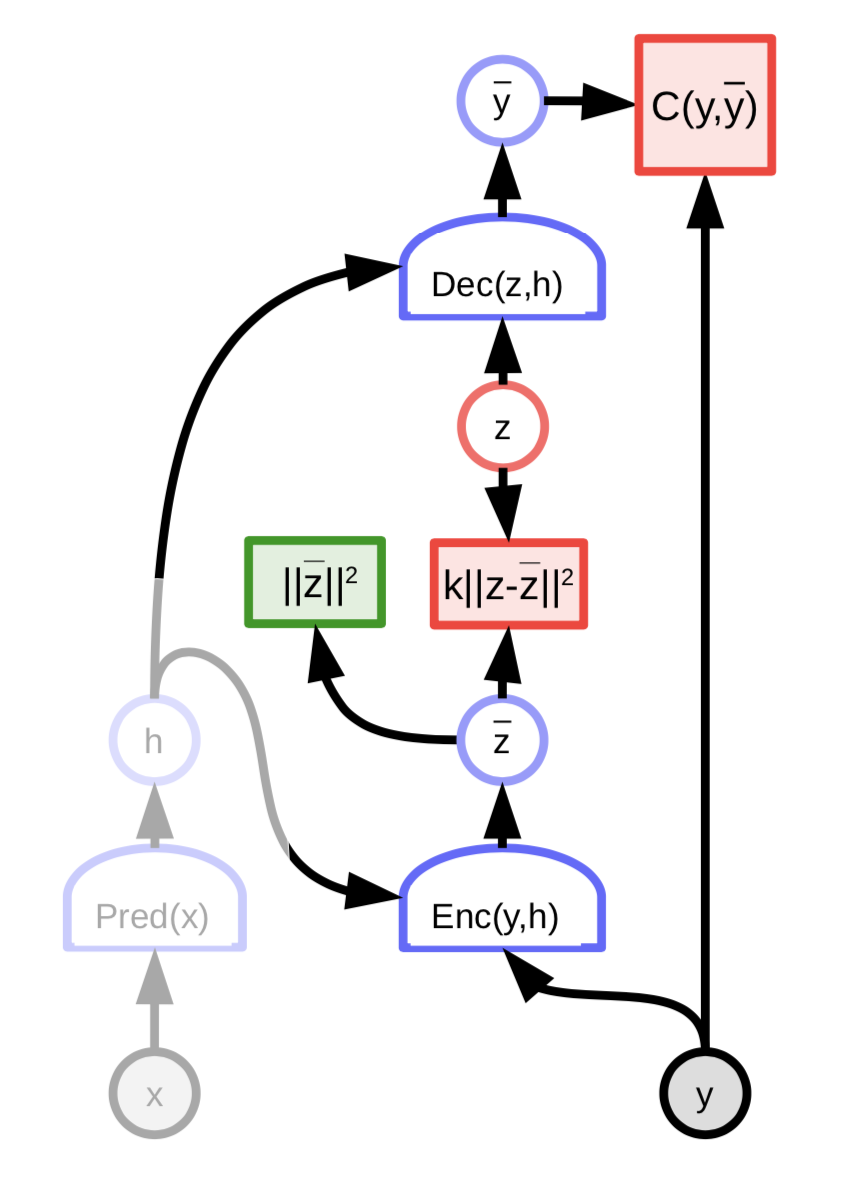
Fig. 8: Arquitectura de un auto-codificador variable.

La variable latente $z$ no es computada a través de minimizar la función de energía con respecto a $z$. Por lo contrario, la función de energía es vista como un muestreo aleatorio $z$ de acuerdo a la distribución cual logaritmo es el costo que la conecta a ${\overline z}$. La distribución es Gaussiana con media ${\overline z}$ y esto resulta en un ruido Gaussiano que es agregado a ${\overline z}$.

Los vectores de código con un ruido Gaussiano agregado pueden ser visualizados como esferas difusas como se muestra en la Fig. 9(a).

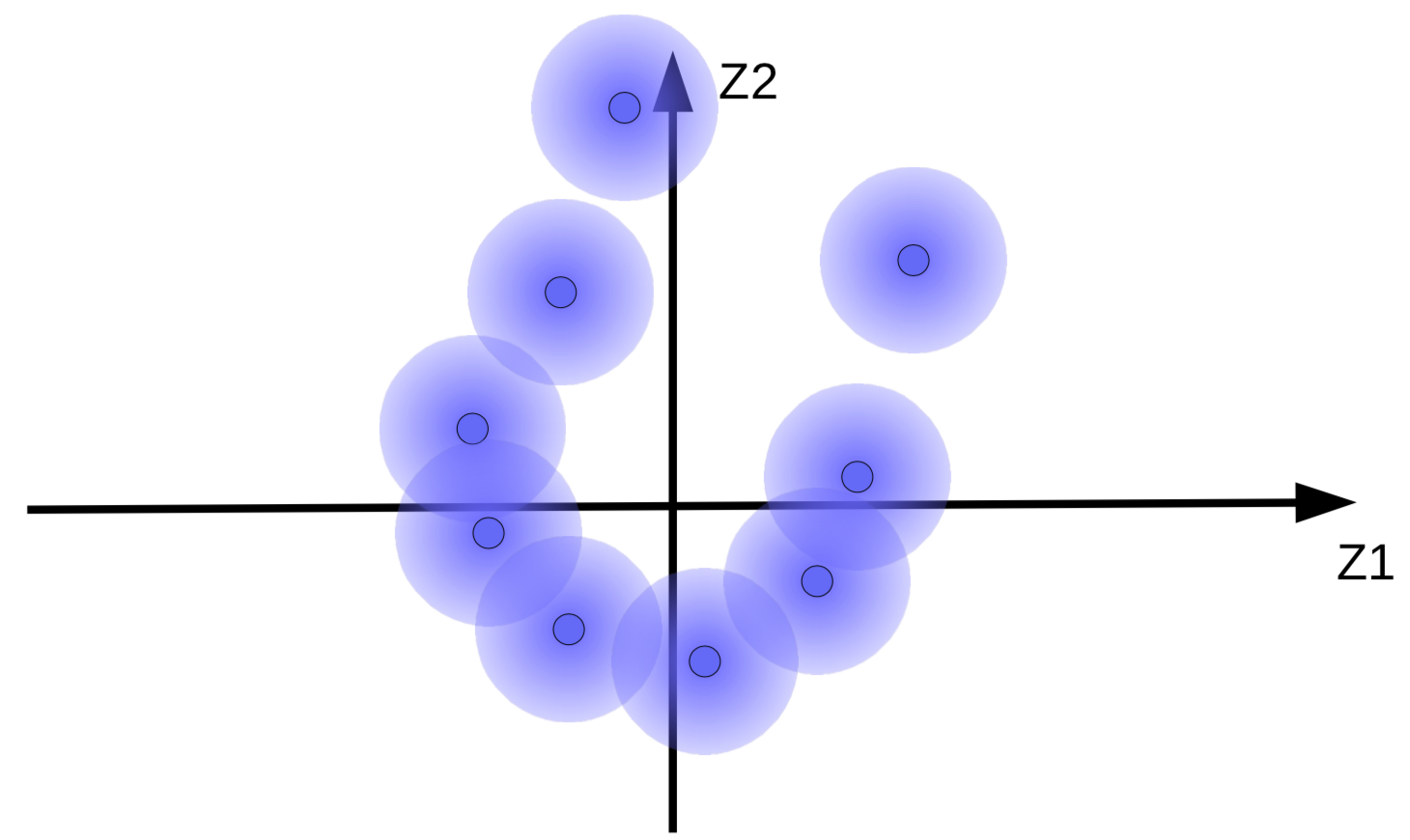(a) Conjunto original de esferas difusas

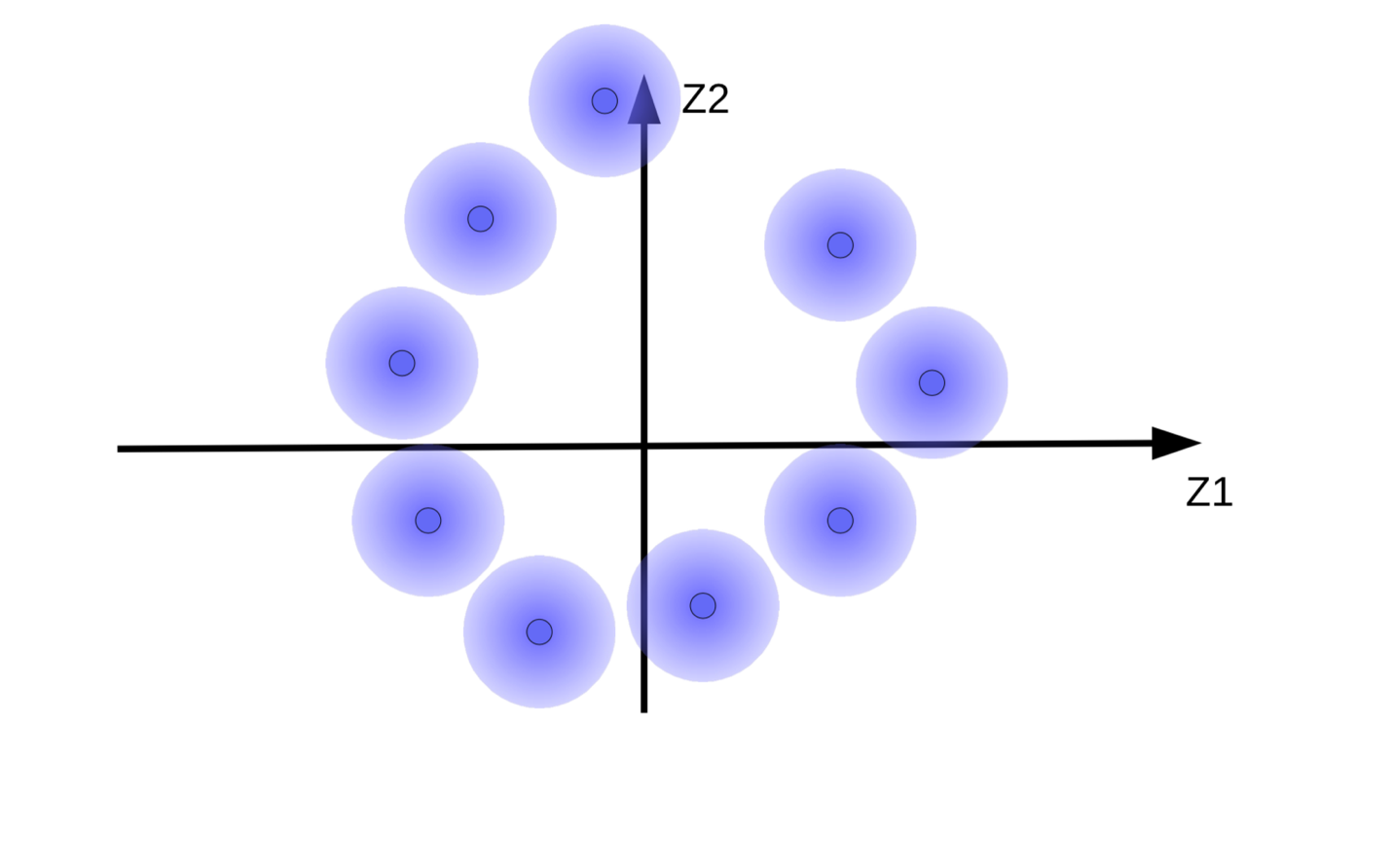(b)Movimiento de las esferas difusas debido a la minimización de energía sin regularización

El sistema intenta hacer los vectores de código ${\overline z}$ tan largos como sea posible para que el efecto en $z$(ruido) sea tan pequeño como sea posible. Ésto resulta en esferas difusas flotando desde el origen como se muestra en la Fig. 9(b). Otra razón por la cual el sistema intenta hacer los vectores de código grandes es para prevenir las esferas difusas superpuestas, lo que causa que el decodificador se confunda entre diferentes muestras durante reconstrucción.

Pero queremos que las besferas difusas se agrupen alrededor de una variedad de datos, si existen. Entonces, los vectores de códigos son regularizados para tener una media y varianza cercana a cero. Para hacer ésto, los conectamos con el origen usando un resorte como se muestra en la Fig. 10.

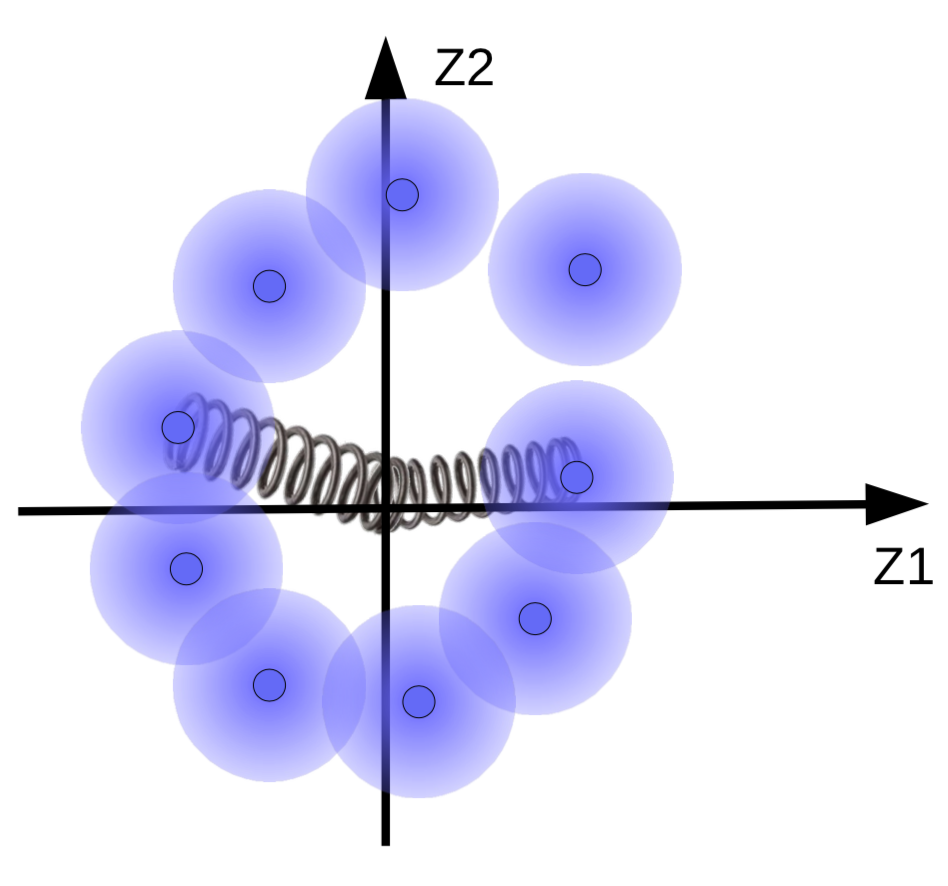
b>Fig. 10</b>: Efectos de la regularización visualizados con resortes

La fuerza del resorte determina que tan cerca las esferas difusas están del origen. Si el resorte es muy débil, entonces las esferas difusas volarían fuera del origen. Si es muy fuerte, entonces colapsarían al origen, resultando en un valor de energía alto. Para prevenir ésto, el sistema deja a las esferas superponerse solo si las muestras correspondientes son similares

También es posible adaptarse al tamaño de las esferas difusas. Ésto es limitado por una función de penalización (Divergencia KL) que intenta hacer la varianza cercana a 1 para que el tamaño de las esferas no sean ni muy grandes ni muy pequeñas que se derrumbe.