Introducción a autoencoders

Aplicación de autoencoders

Generación de imágenes

¿Puedes decir qué cara es falsa en la Fig. 1? De hecho, ambos son producidos por el generador StyleGan2. Aunque los detalles faciales son muy realistas, el fondo parece extraño (izquierda: borrosidad, derecha: objetos deformados). Esto se debe a que la red neuronal se entrena en muestras de caras. El fondo tiene entonces una variabilidad mucho mayor. Aquí, la variedad de datos tiene aproximadamente 50 dimensiones, iguales a los grados de libertad de una imagen facial.

Fig. 1: Caras generadas a partir de StyleGan2

Diferencia de interpolación en el espacio de píxeles y el espacio latente

Fig. 2: Un perro y un pájaro

Si interpolamos linealmente entre la imagen del perro y el pájaro (Fig. 2) en el espacio de píxeles, obtendremos una superposición difusa de dos imágenes en la Fig. 3. Desde la parte superior izquierda a la inferior derecha, el peso de la imagen del perro disminuye y el peso de la imagen del pájaro aumenta.

Fig. 3: Resultados después de la interpolación

Si interpolamos en dos representaciones de espacios latentes y los alimentamos al decodificador, obtendremos la transformación de perro a pájaro en la Fig.4.

Fig. 4: Resultados después de alimentar al decodificador

Obviamente, el espacio latente es mejor para capturar la estructura de una imagen.

Ejemplos de transformación

Fig. 5: Magnificación

Fig. 6: Cambio de posición

Fig. 7: Cambio de brillo

Fig. 8: Rotación (tenga en cuenta que la rotación podría ser 3D)

Súper resolución de images

Este modelo tiene como objetivo mejorar la calidad de las imágenes y reconstruir los rostros originales. De izquierda a derecha en la Fig. 9, la primera columna es la imagen de entrada de 16x16, la segunda es lo que obtendría de una interpolación bicúbica estándar, la tercera es la salida generada por la red neuronal y a la derecha estám casos reales. (https://github.com/david-gpu/srez)

Fig. 9: Reconstruyendo caras originales

A partir de las imágenes de salida, queda claro que existen sesgos en los datos de entrenamiento, lo que hace que las caras reconstruidas sean inexactas. Por ejemplo, el hombre asiático de arriba a la izquierda está hecho para parecer europeo en la salida debido a las imágenes de entrenamiento desequilibradas. La cara reconstruida de las mujeres de abajo a la izquierda se ve extraña debido a la falta de imágenes desde ese ángulo extraño en los datos de entrenamiento.

Repintado de images

Fig. 10: Poniendo parche gris en las caras

Poniendo un parche gris en la cara como en la Fig. 10 hace que la imagen se aleje de las variedades de los ejemplos de entrenamiento. La reconstrucción de la cara en la Fig. 11 se realiza encontrando la imagen de muestra más cercana en las variedades de los ejemplos de entrenamiento a través de la minimización de la función de energía.

Fig. 11: Imagen reconstruida de Fig. 10

Subtítulos a imagen

Fig. 12: Ejemplo de subtítulo a imagen

El traslado desde descripción de texto a imagen en la Fig. 12 se logra extrayendo las representaciones de características de texto asociadas con información visual importante y luego decodificándolas en imágenes.

¿Qué son los autoencoders?

Los autoencoders son redes neuronales artificiales, entrenadas de manera no supervisada, que tienen como objetivo aprender primero las representaciones codificadas de nuestros datos y luego generar los datos de entrada (lo más cerca posible) a partir de las representaciones codificadas aprendidas. Por tanto, la salida de de autoencoder es su predicción para la entrada.

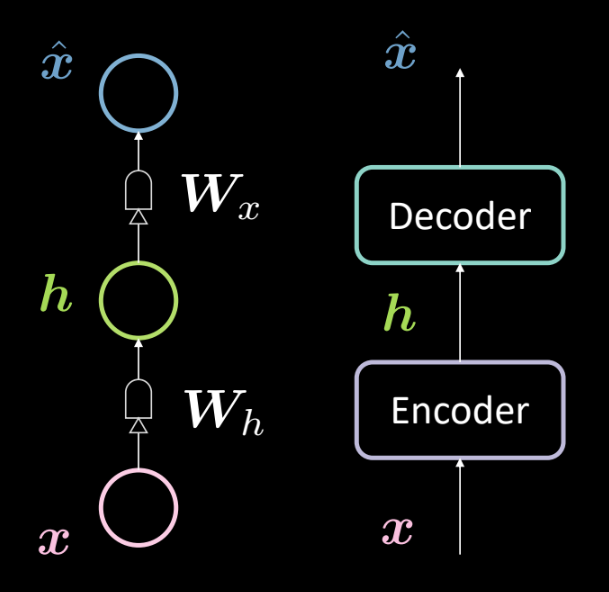
Fig. 13: Arquitectura de un autoencoder básico

La Fig. 13 muestra la arquitectura de un autoencoder básico. Como antes, comenzamos desde abajo con la entrada $\boldsymbol{x}$ que está sujeta a un codificador (transformación afín definida por $\boldsymbol{W_h}$, seguido de un “apretón”). Esto da como resultado la capa oculta intermedia $\boldsymbol{h}$. Esto se somete al decodificador (otra transformación afín definida por $\boldsymbol{W_x}$ seguida de otro “apretón”). Esto produce la salida $\boldsymbol{\hat{x}}$, que es la predicción/reconstrucción de la entrada de nuestro modelo. Según nuestra convención, decimos que se trata de una red neuronal de 3 capas.

Podemos representar la red anterior matemáticamente usando las siguientes ecuaciones:

También especificamos las siguientes dimensionalidades:

Nota: Para representar los componentes principales (principal component analysis, PCA), podemos tener pesos ajustados (o pesos atados) definidos por $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$

¿Por qué utilizamos autoencoders?

A este punto, es posible que te preguntes cuál es el sentido de predecir la entrada y cuáles son las aplicaciones de autoencoders.

Las aplicaciones principales de un autoencoder son la detección de anomalías o la eliminación de ruido de imágenes. Sabemos que la tarea de un autoencoder es poder reconstruir datos que viven en variedad, es decir, dado una variedad de datos, querríamos que nuestro autoencoder pudiera reconstruir solo la entrada que existe en esa variedad. Por lo tanto, restringimos el modelo para reconstruir cosas que se han observado durante el entrenamiento, por lo que cualquier variación presente en las nuevas entradas se eliminará porque el modelo sería insensible a ese tipo de perturbaciones.

Otra aplicación de un autoencoder es como un compresor de imágenes. Si tenemos una dimensionalidad intermedia $d$ menor que la dimensionalidad de entrada $n$, entonces el codificador puede usarse como un compresor y las representaciones ocultas (representaciones codificadas) abordarían toda (o la mayoría) de la información en la entrada específica pero ocupa menos espacio.

Función de costo de reconstrucción

Veamos ahora las funciones de costo de reconstrucción que usamos generalmente. La función de costo general para el conjunto de datos se da como el promedio por costo de muestra, es decir,

Cuando la entrada es categórica, podríamos usar la función de costo de entropía cruzada (cross-entropy) para calcular el costo por muestra que viene dada por

Y cuando la entrada tiene un valor real, es posible que deseemos usar la función de costo de error cuadrático medio dada por

Capa oculta subcompleta o sobrecompleta

Cuando la dimensionalidad de la capa oculta $d$ es menor que la dimensionalidad de la entrada $n$, decimos que esta capa oculta esta subcompleta. Y de manera similar, cuando $d>n$, lo llamamos una capa oculta sobrecompleta. La Fig. 14 muestra una capa oculta subcompleta a la izquierda y una capa oculta sobrecompleta a la derecha.

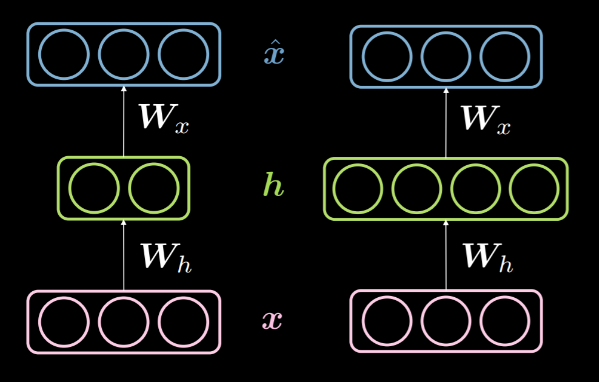
Fig. 14: Una capa oculta subcompleta vs una sobrecompleta

Como se mencionó anteriormente, se puede usar una capa oculta subcompleta para la compresión, ya que estamos codificando la información de entrada en menos dimensiones. Por otro lado, en una capa sobrecompleta, usamos una codificación con mayor dimensionalidad que la entrada. Esto facilita la optimización.

Dado que estamos tratando de reconstruir la entrada, el modelo es propenso a copiar todas las características de entrada en la capa oculta y pasarla como salida, por lo que se comporta esencialmente como una función de identidad. Esto debe evitarse, ya que esto implicaría que nuestro modelo no aprende nada. Por lo tanto, necesitamos aplicar algunas restricciones adicionales mediante la aplicación de un cuello de botella de información. Hacemos esto restringiendo las posibles configuraciones que la capa oculta puede tomar a solo aquellas configuraciones vistas durante el entrenamiento. Esto permite una reconstrucción selectiva (limitada a un subconjunto del espacio de entrada) y hace que el modelo sea insensible a todo lo que no está en la variedad.

Cabe señalar que una capa subcompleta no puede comportarse como una función de identidad simplemente porque la capa oculta no tiene suficientes dimensiones para copiar la entrada. Por lo tanto, es menos probable que una capa oculta subcompleta se sobreajuste en comparación con una capa oculta sobrecompleta, pero aún así podría sobreajustarse. Por ejemplo, dado un codificador y un decodificador potentes, el modelo podría simplemente asociar un número a cada punto de datos y aprender el mapeo. Existen varios métodos para evitar el sobreajuste, como los métodos de regularización, los métodos arquitectónicos, etc.

Autoencoder eliminador de ruido

La Fig.15 muestra la variedad del autoencoder eliminador de ruido y la intuición de cómo funciona.

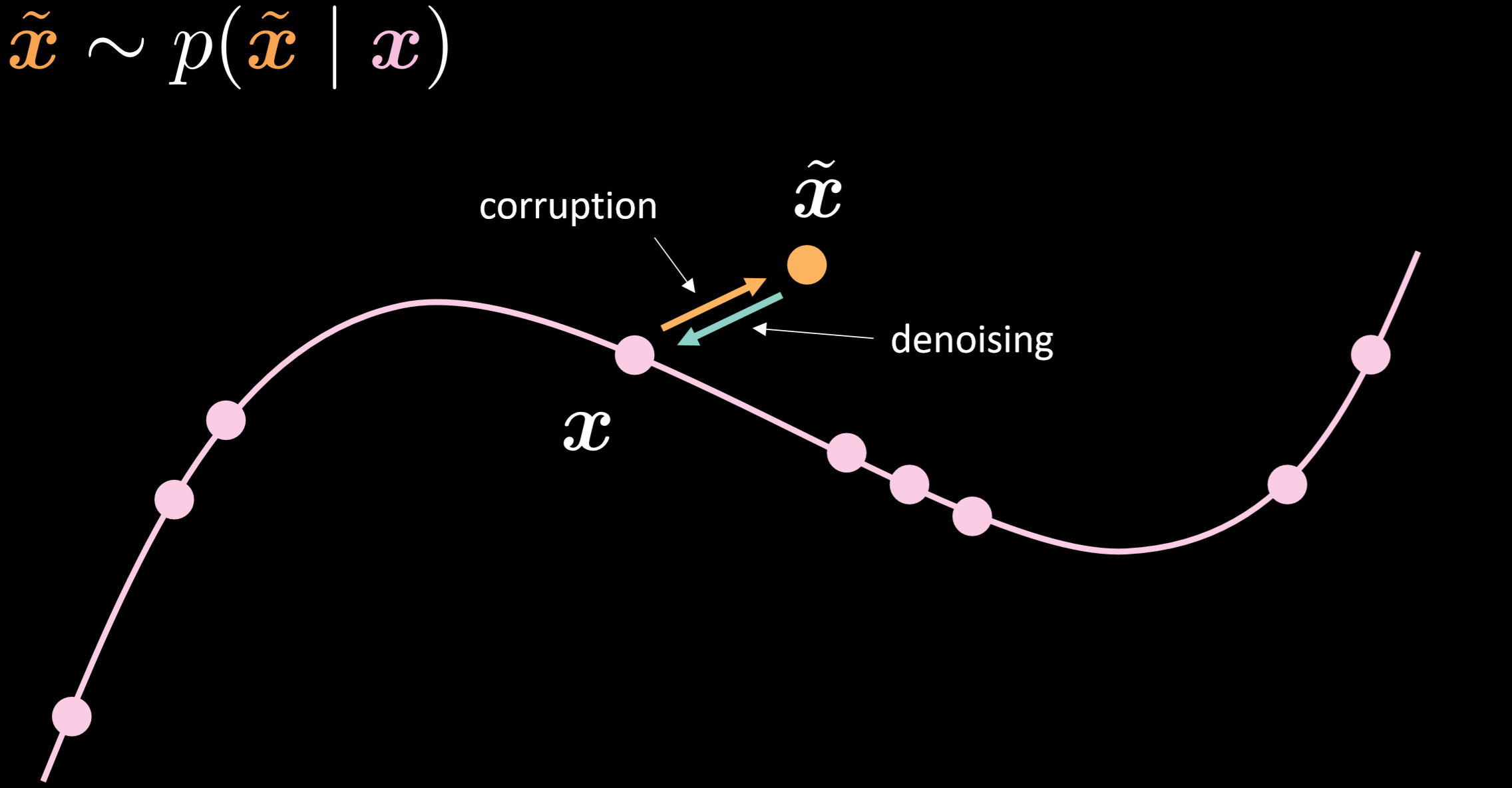
Fig. 15: Autoencoder eliminador de ruido

En este modelo, asumimos que estamos inyectando la misma distribución ruidosa que vamos a observar en la realidad, de modo que podamos aprender cómo recuperarnos de ella de manera robusta. Al comparar la entrada y la salida, podemos decir que los puntos que ya estaban en los datos de la variedad no se movieron, y los puntos que estaban lejos de la variedad se movieron mucho.

La Fig.16 muestra la relación entre los datos de entrada y los datos de salida.

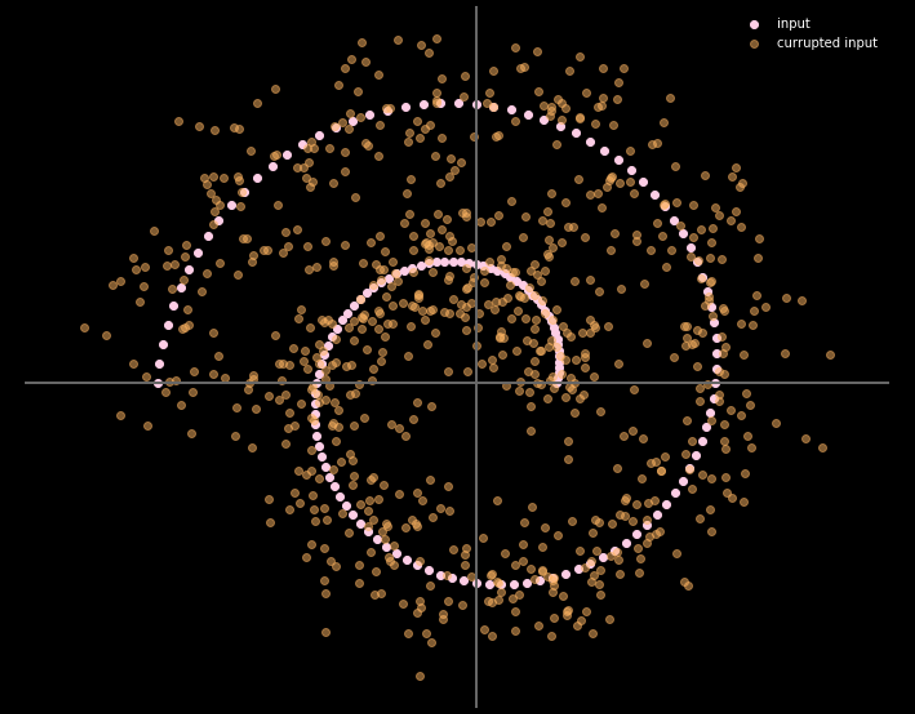
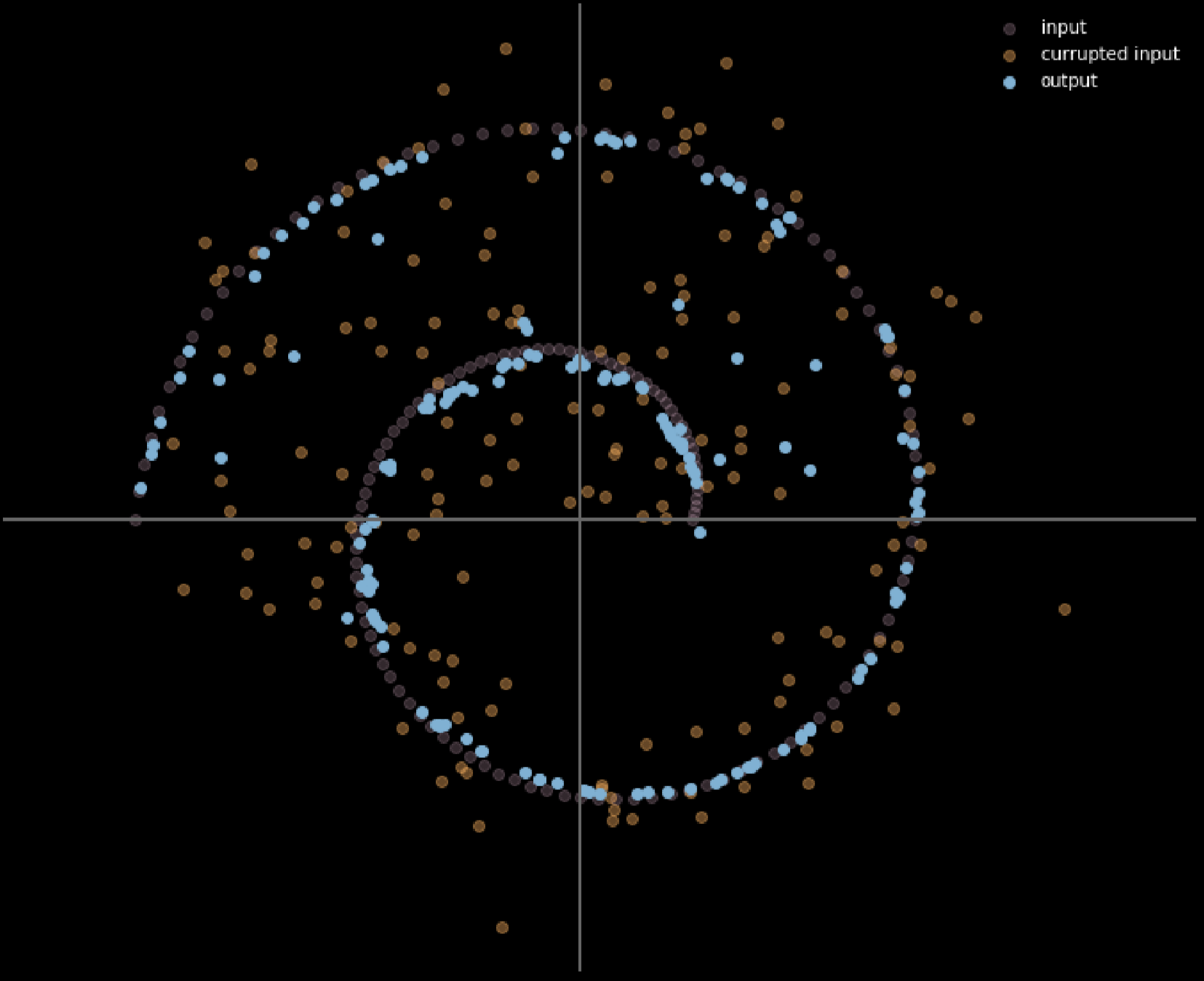
Fig. 16: Entrada y salida del autoencoder eliminador de ruido

También podemos usar diferentes colores para representar la distancia de los movimientos de cada punto de entrada, la Fig. 17 muestra el diagrama.

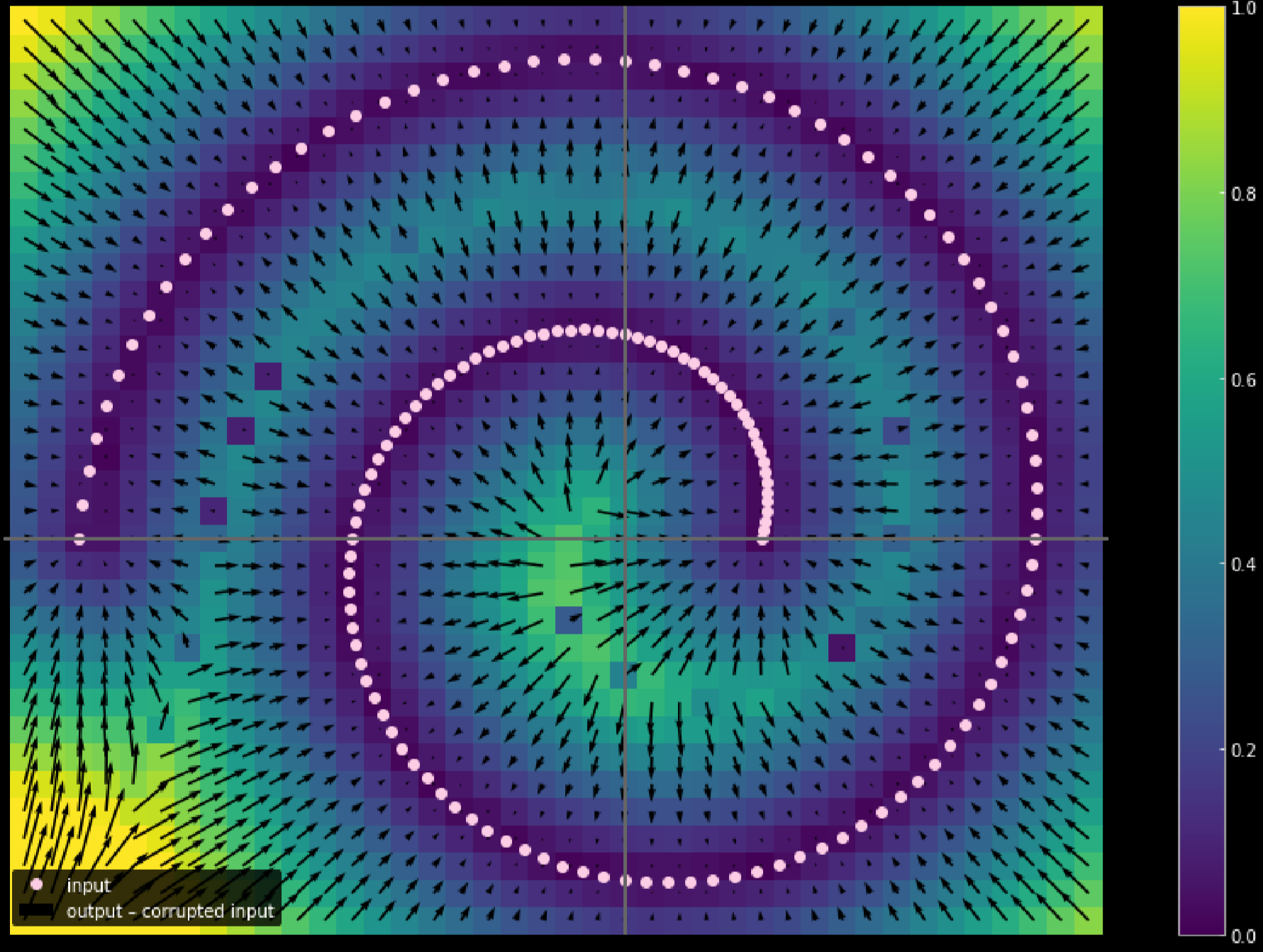
Fig. 17: Medir la distancia de viaje de los datos de entrada

Cuanto más claro sea el color, mayor será la distancia recorrida por un punto. Del diagrama, podemos decir que los puntos en las esquinas viajaron cerca de 1 unidad, mientras que los puntos dentro de las 2 ramas no se movieron en absoluto ya que son atraídos por las ramas superior e inferior durante el proceso de entrenamiento.

Autoencoder contractivo

La Fig.18 muestra la función de costo del autoencoder contractivo y la variedad.

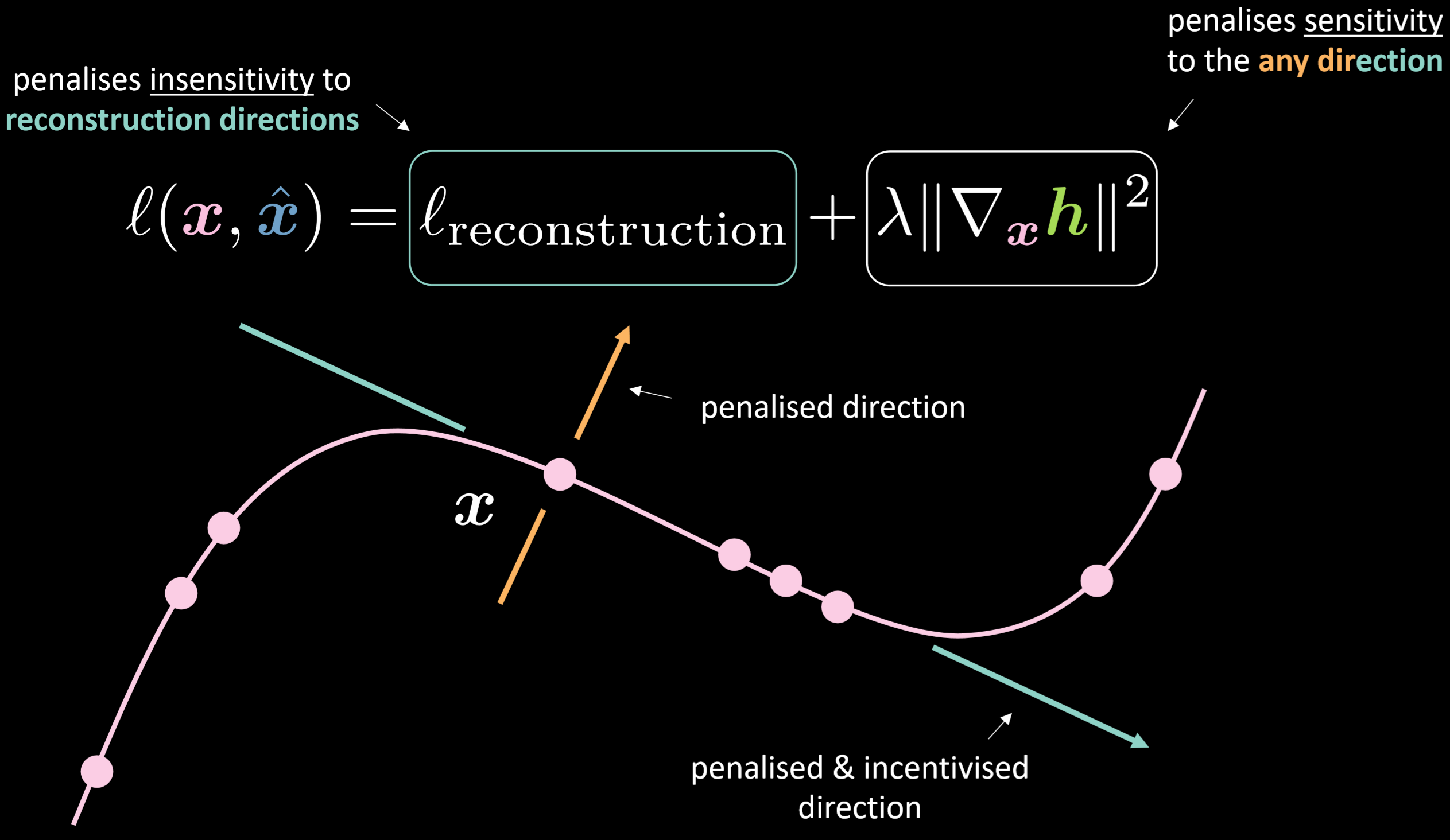
Fig. 18: Autoencoder contractivo

La función de costo contiene el término de reconstrucción más la norma al cuadrado del gradiente de la representación oculta con respecto a la entrada. Por lo tanto, la función de costo general minimizará la variación de la capa oculta dada la variación de la entrada. El beneficio sería hacer que el modelo sea sensible a las direcciones de reconstrucción mientras que insensible a cualquier otra dirección posible.

La Fig.19 muestra cómo funcionan estos autoencoders en general.

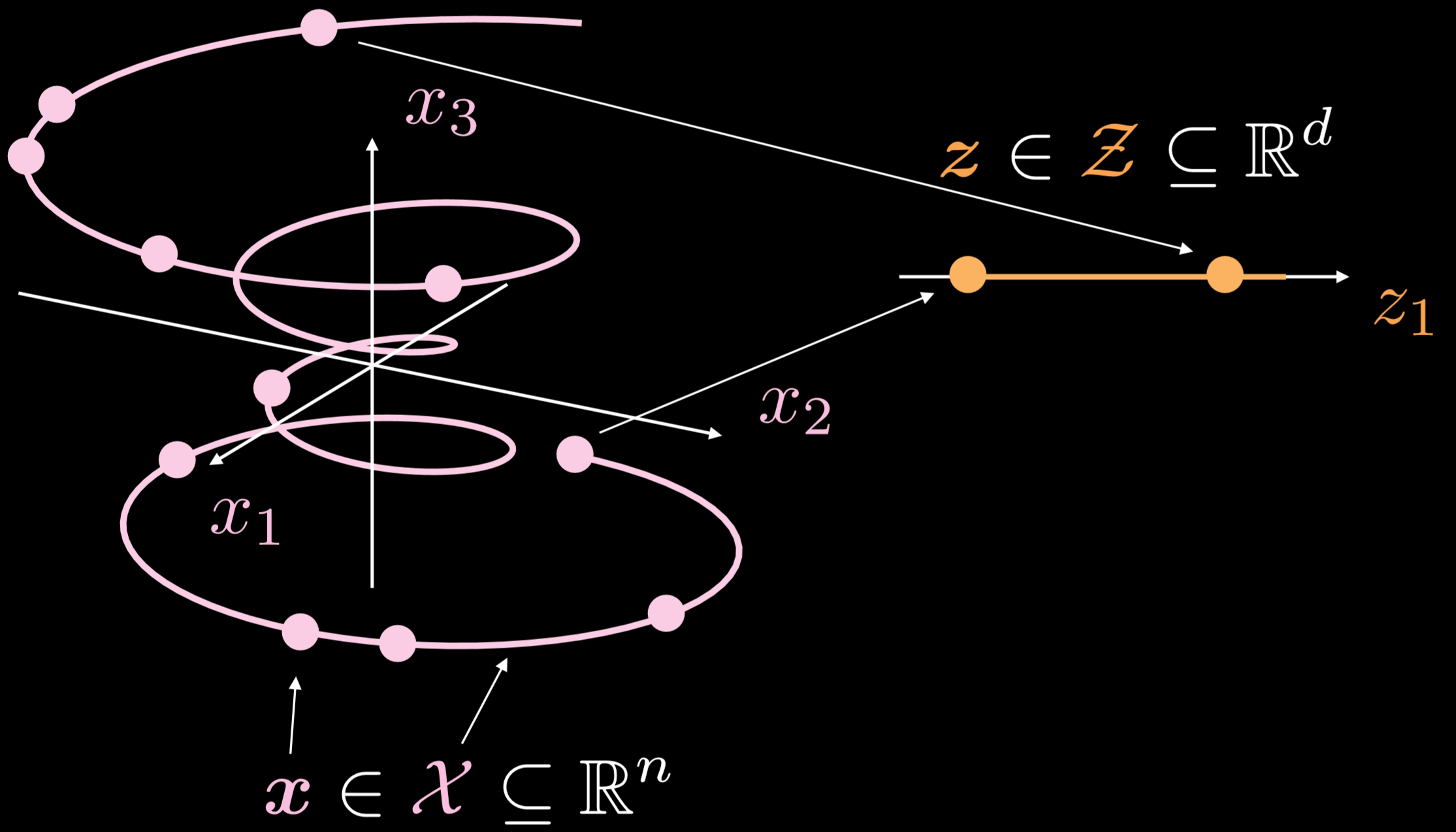
Fig. 19: Autoencoder básico

La variedades de los ejemplos de entrenamiento es un objeto unidimensional que va en tres dimensiones. Donde $\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$, el objetivo del autoencoder es estirar la línea curveada en una dirección, donde $\boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$. Como resultado, un punto de la capa de entrada se transformará en un punto de la capa latente. Ahora tenemos la correspondencia entre los puntos en el espacio de entrada y los puntos en el espacio latente, pero no tenemos la correspondencia entre las regiones del espacio de entrada y las regiones del espacio latente. Luego, utilizaremos el decodificador para transformar un punto de la capa latente para generar una capa de salida significativa.

Implementar un autoencoder - Notebook

El Jupyter Notebook se puede encontrar aquí.

En este Notebook, vamos a implementar un autoencoder estándar y un autoencoder eliminador de ruido y luego compararemos las salidas.

Definir la arquitectura del modelo de autoencoder y la función de costo de reconstrucción

Usando una imagen de $28 \times 28$, y una capa oculta de 30 dimensiones. La rutina de transformación estaría pasando de $784\to30\to784$. Al aplicar la función de tangente hiperbólica a la rutina del codificador y decodificador, podemos limitar el rango de salida a $(-1, 1)$. El error cuadrático medio (Mean Squared Error, MSE) se utilizará como función de costo de este modelo.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

Entrenar autoencoder estándar

Para entrenar un autoencoder estándar usando PyTorch, necesitas poner los siguientes 5 métodos en el bucle de entrenamiento:

Yendo hacia adelante:

1) Enviar la imagen de entrada a través del modelo llamando output = model(img) .
2) Calcule la función de costo usando: criterion(output, img.data).

Yendo hacia atrás:

3) Borre el gradiente para asegurarse de que no acumulemos el valor: optimizer.zero_grad().
4) Propagación hacia atrás: loss.backward()
5) Paso hacia atrás: optimizer.step()

La Fig. 20 muestra la salida del autoencoder estándar.

Fig. 20: Salida del autoencoder estándar

Entrenar un autoencoder eliminador de ruido

Para el autoencoder eliminador de ruido, necesitas agregar los siguientes pasos:
1) LLamar nn.Dropout() para apagar neuronas aleatoriamente.
2) Crear máscara de ruido: do(torch.ones(img.shape)).
3) Crear imágenes malas multiplicando imágenes buenas por máscaras binarias: img_bad = (img * noise).to(device).

La Fig. 21 muestra la salida del autoencoder eliminador de ruido.

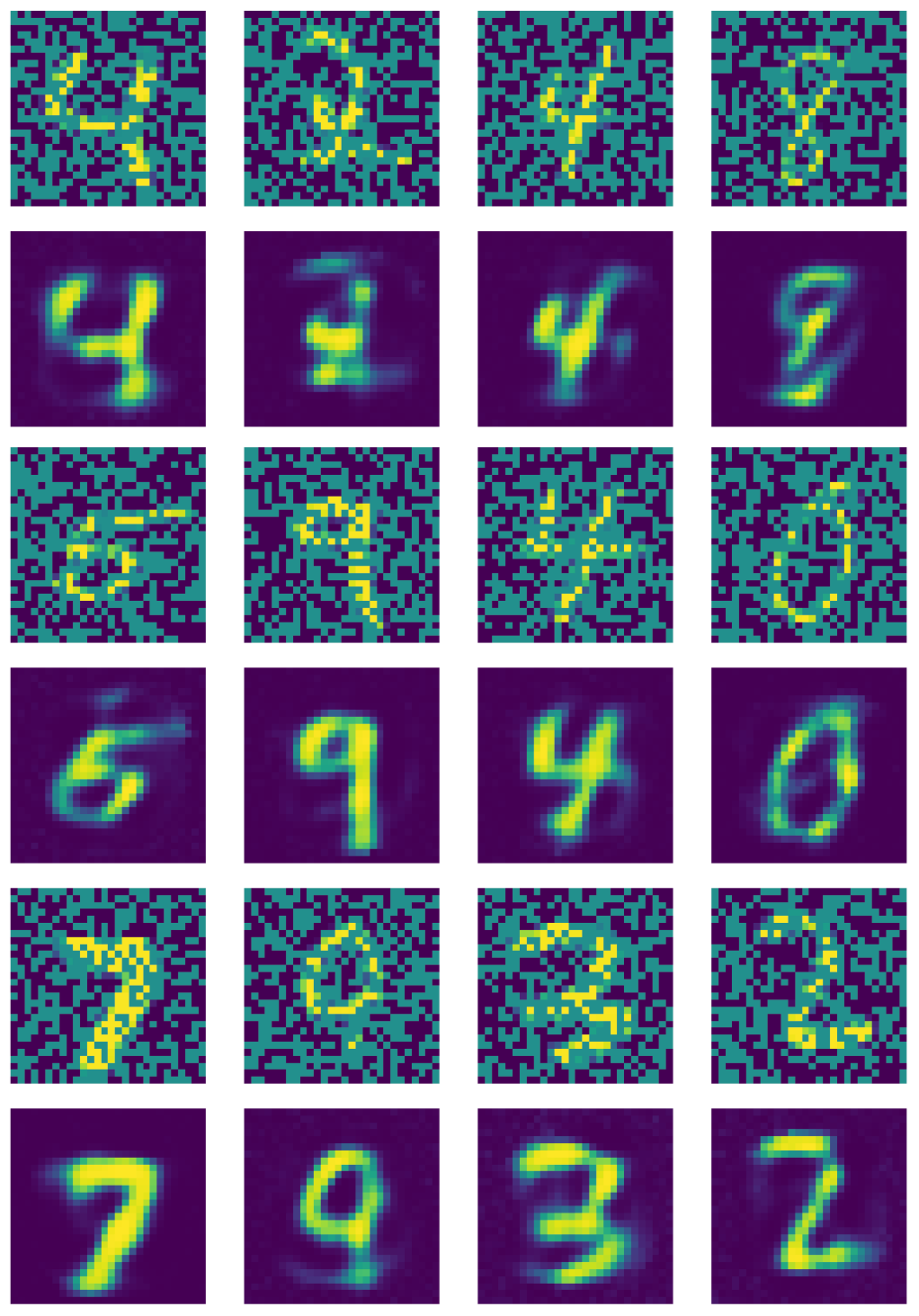
Fig. 21: Salida del autoencoder eliminador de ruido

Comparación de kernels

Es importante tener en cuenta que a pesar del hecho de que la dimensión de la capa de entrada es $28 \times 28 = 784$, una capa oculta con una dimensión de 500 sigue siendo una capa sobrecompleta debido a la cantidad de píxeles negros en la imagen. A continuación se muestran ejemplos de kernels utilizados en el autoencoder estándar subcompleto entrenado. Claramente, los píxeles en la región donde existe el número indican la detección de algún tipo de patrón, mientras que los píxeles fuera de esta región son básicamente aleatorios. Esto indica que el autoencoder estándar no se preocupa por los píxeles fuera de la región donde está el número.

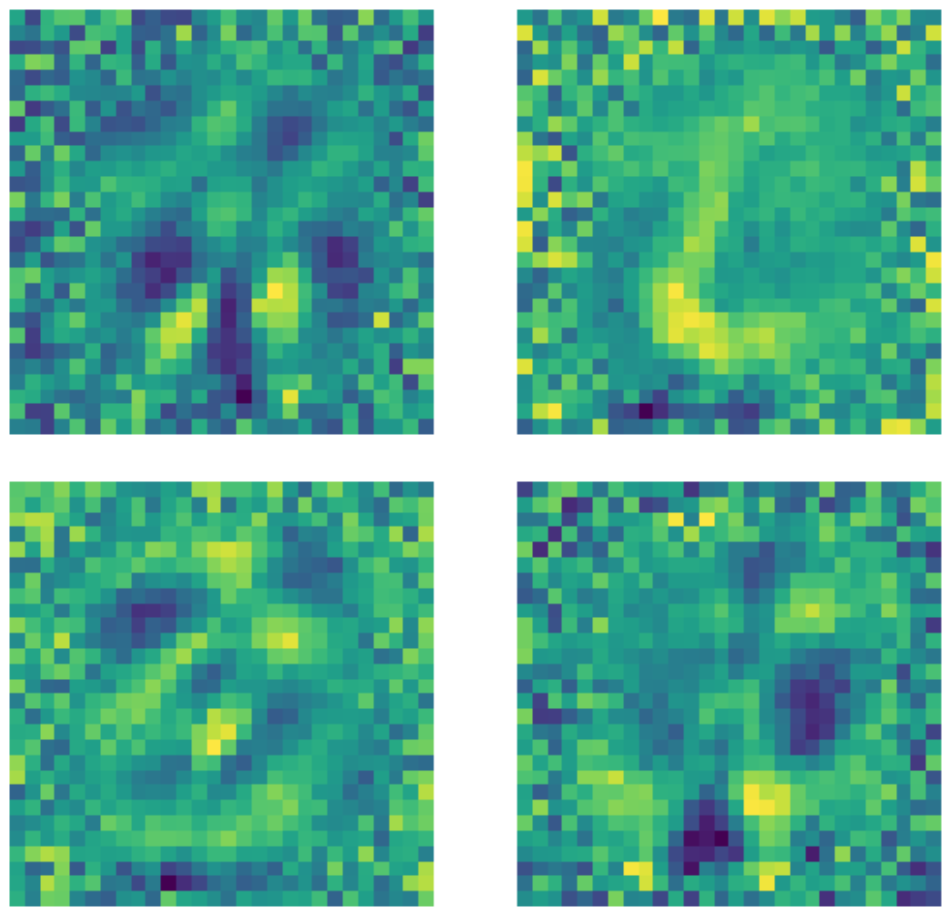
Figure 22: Kernels de autoencoders estándares.

Por otro lado, cuando los mismos datos se envían a un autoencoder eliminador de ruido donde se aplica una máscara de dropout a cada imagen antes de ajustar el modelo, sucede algo diferente. Cada kernel que aprende un patrón establece los píxeles fuera de la región donde existe el número en algún valor constante. Debido a que se aplica una máscara de dropout a las imágenes, el modelo ahora se preocupa por los píxeles fuera de la región del número.

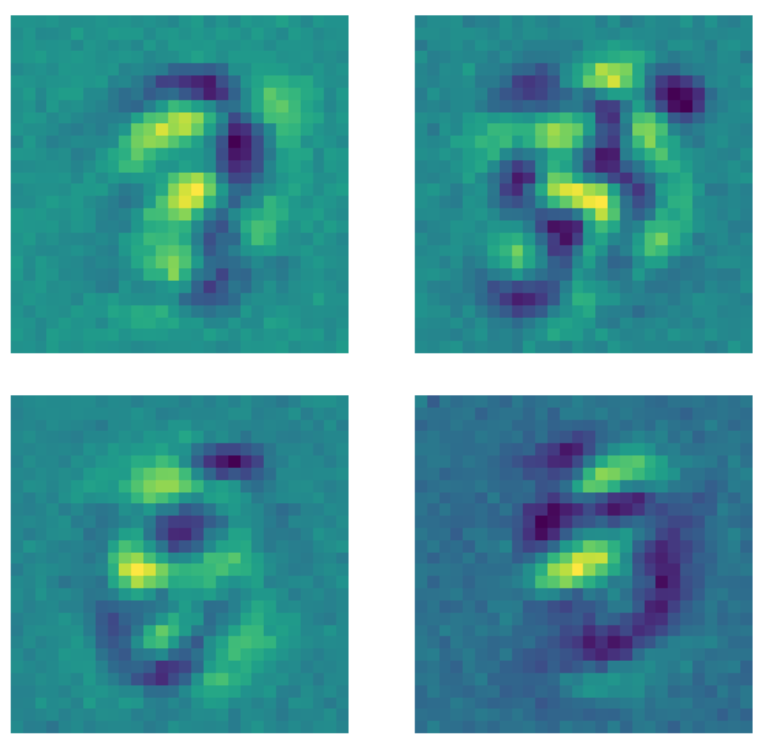
Figure 23: Kernels de autoencoders eliminadores de ruido.

En comparación con el estado del arte, ¡nuestro autoencoder funciona mejor! Puedes ver los resultados a continuación.

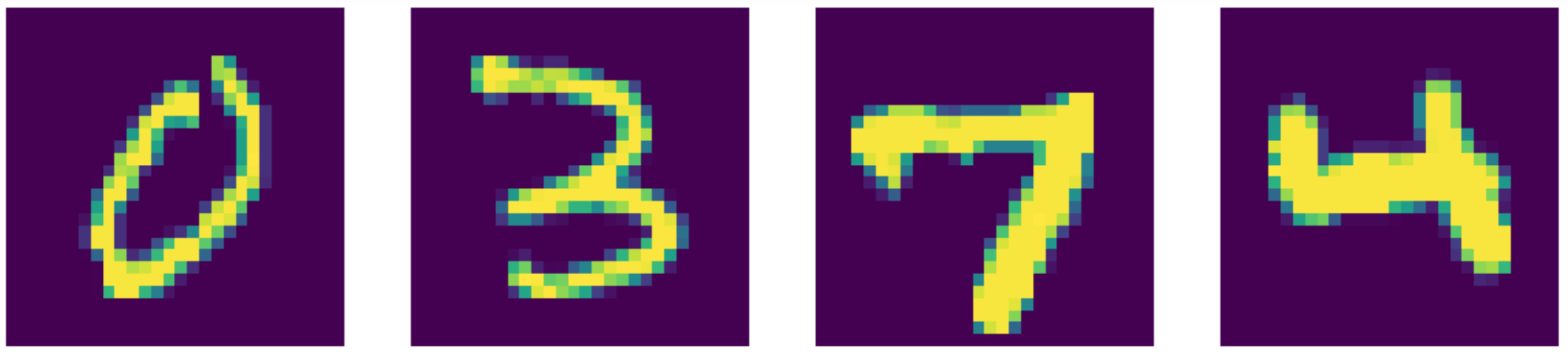
Figure 24: Datos de entrada (dígitos MNIST).

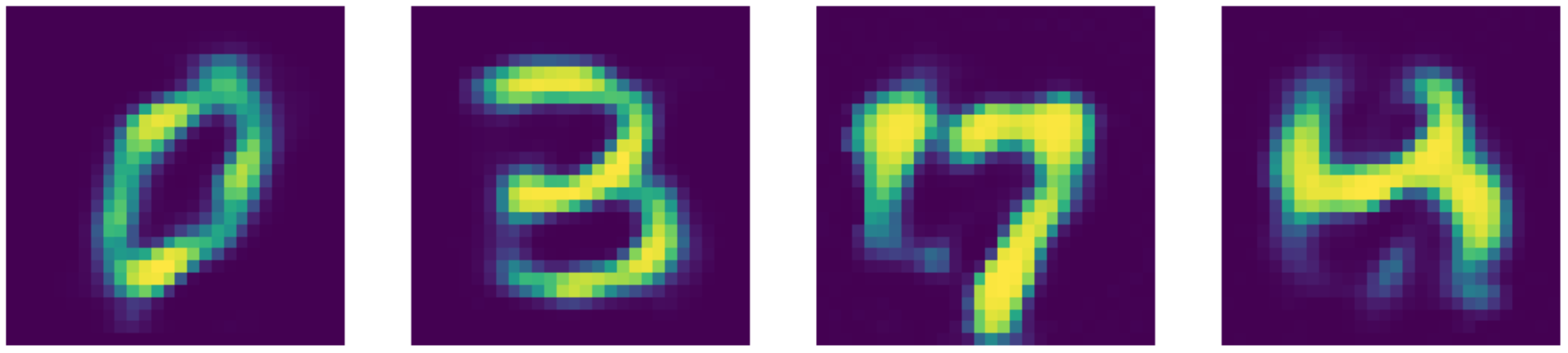
Figure 25: Reconstrucciones de autoencoders eliminadores de ruido.

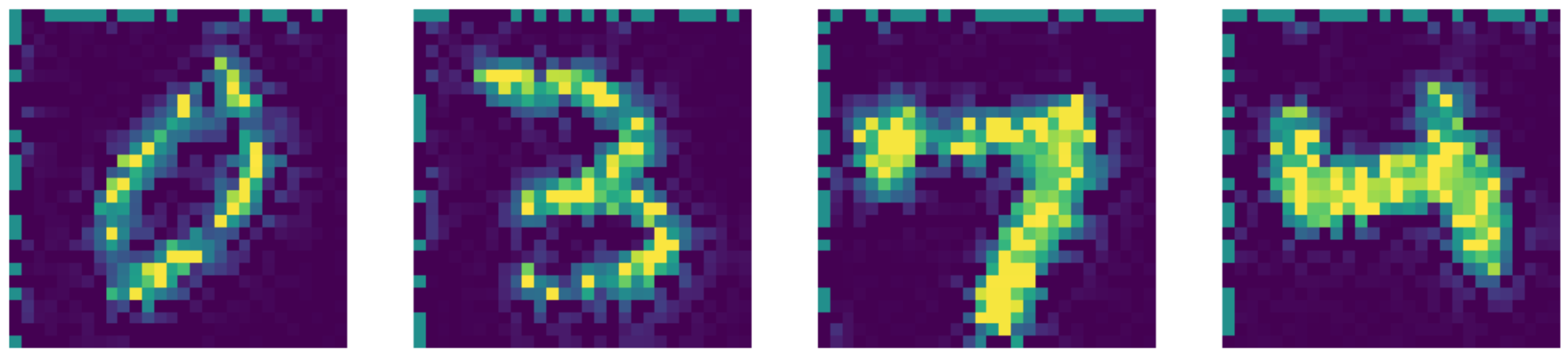
Figure 26: Salida del repintado de images using el método de Telea.

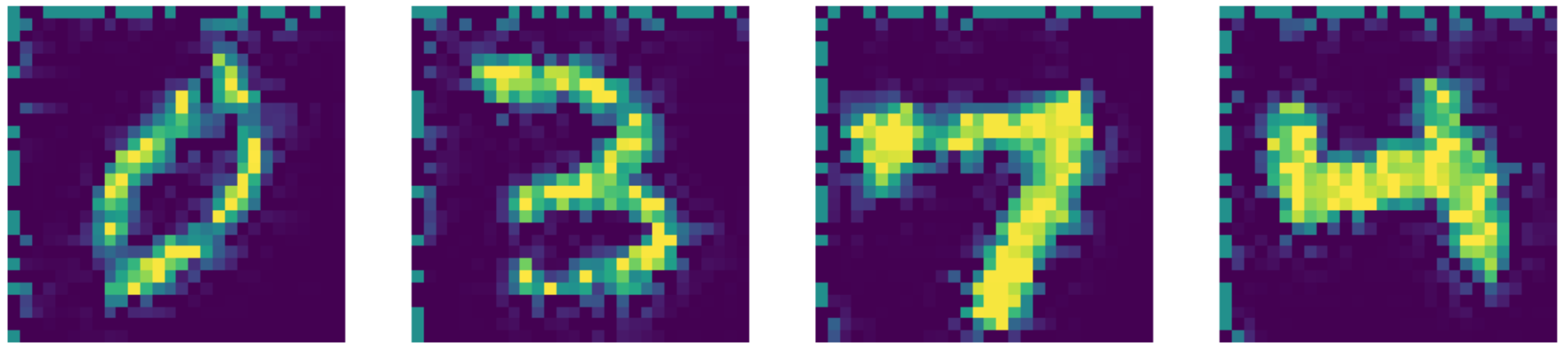
Figure 27: Salida del repintado de images using el método de Navier-Stokes.