SSL, EBM con detalles y ejemplos

Aprendizaje auto supervisado

El aprendizaje auto supervisado (self-supervised learning, SSL) abarca tanto el aprendizaje supervisado como el no supervisado. El objetivo de la tarea de pretexto SSL es aprender una buena representación de la entrada para que posteriormente pueda utilizarse para tareas supervisadas. En SSL, el modelo está entrenado para predecir una parte de los datos dadas otras partes de los datos. Por ejemplo, BERT fue entrenado usando técnicas SSL y de autoencoder eliminador de ruido (Denoising Auto-Encoder, DAE) ha particularmente mostrado resultados en el estado del arte en el procesamiento del lenguaje natural (Natural Language Processing, NLP).

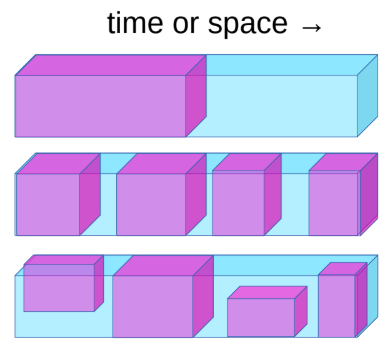
Fig. 1: Aprendizaje auto supervisado

La tarea de aprendizaje auto supervisado se puede definir como sigue:

• Predecir el futuro desde el pasado.
• Predecir lo enmascarado desde lo visible.
• Predecir las partes ocluidas desde todas las partes disponibles.

Por ejemplo, si un sistema está entrenado para predecir el siguiente fotograma cuando se mueve la cámara, el sistema aprenderá implícitamente sobre la profundidad y el paralaje. Esto obligará al sistema a aprender que los objetos ocluidos de su visión no desaparecen sino que continúan existiendo y la distinción entre objetos animados e inanimados y el fondo. También puede terminar aprendiendo sobre física intuitiva como la gravedad.

El estado del arte de sistemas NLP (BERT) pre-entrenan una red neuronal gigante en una tarea de SSL. Tu eliminas algunas de las palabras de una oración y hace que el sistema prediga las palabras que faltan. Esto ha tenido mucho éxito. También se probaron ideas similares en el ámbito de la visión por computadora. Como se muestra en la imagen a continuación, puedes tomar una imagen y eliminar una parte de la imagen y entrenar el modelo para predecir la parte que falta.

Fig. 2: Resultados correspondientes en visión por computadora

Aunque los modelos pueden llenar el espacio que falta, ellos no han compartido el mismo nivel de éxito que los sistemas NLP. Si tuviera que tomar las representaciones internas generadas por estos modelos, como entrada a un sistema de visión por computadora, no podría vencer a un modelo que fue pre-entrenado de manera supervisada en ImageNet. La diferencia aquí es que NLP es discreto mientras que las imágenes son continuas. La diferencia en el éxito se debe a que en el dominio discreto sabemos cómo representar la incertidumbre, podemos usar un gran softmax sobre las posibles salidas, en el dominio continuo no lo hacemos.

Un sistema inteligente (agente de IA) necesita poder predecir los resultados de su propia acción en el entorno y a sí mismo para tomar decisiones inteligentes. Dado que el mundo no es completamente determinista y no hay suficiente poder de cómputo en una máquina / cerebro humano para tener en cuenta todas las posibilidades, debemos enseñar a los sistemas de IA a predecir en presencia de incertidumbre en espacios de gran dimensión. Los modelos basados ​​en energía (EBM) pueden ser extremadamente útiles para esto.

Una red neuronal entrenada con mínimos cuadrados para predecir el siguiente fotograma de un video dará como resultado imágenes borrosas porque el modelo no puede predecir exactamente el futuro, por lo que aprende a promediar todas las posibilidades del siguiente fotogramas a partir de los datos de entrenamiento para reducir la pérdida.

Modelos basados en energía de variable latente como una solución para hacer predicciones para el siguiente fotograma:

A diferencia de regresión lineal, los modelos basados en energía de variable latente toman lo que sabemos sobre el mundo así como una variable latente que nos da información sobre lo que sucedió en la realidad. Se puede utilizar una combinación de esas dos piezas de información para hacer una predicción cercana a lo que realmente ocurre.

Estos modelos se pueden considerar como sistemas que clasifican la compatibilidad entre la entrada $x$ y la salida real $y$ dependiendo de la predicción utilizando la variable latente que minimiza la energía del sistema. Observa la entrada $x$ y produce posibles predicciones $\bar{y}$ para diferentes combinaciones de entrada $x$ y variables latentes $z$ y elige la que minimiza la energía, el error de predicción, del sistema.

Dependiendo de la variable latente que dibujemos, podemos terminar con todas las predicciones posibles. La variable latente podría considerarse como una pieza de información importante sobre la salida $y$ que no está presente en la entrada $x$.

La función de energía de valor escalar puede tomar dos versiones:

1. Ccondicional $F(x, y)$ - mide la compatibilidad entre $x$ y $y$
2. Incondicional $F(y)$ - mide la compatibilidad entre los componentes de $y$

Entrenando un modelo basado en energía

Hay dos clases de modelos de aprendizaje para entrenar un modelo basado en energía para parametrizar $F(x, y)$.

1. Métodos contrastivos: Empuja hacia abajo en $F(x[i], y[i])$, empuja hacia arriba en otros puntos $F(x[i], y’)$
2. Métodos arquitectónicos: Construir $F(x, y)$ para que el volumen de las regiones de baja energía se limite o minimice mediante regularización

Hay siete estrategias para dar forma a la función de energía. Los métodos contrastivos difieren en la forma en que seleccionan los puntos para empujar hacia arriba. Mientras que los métodos arquitectónicos difieren en la forma en que limitan la capacidad de información del código.

Un ejemplo del método contrastivo es el aprendizaje de máxima verosimilitud. La energía se puede interpretar como una densidad logarítmica negativa no normalizada. La distribución de Gibbs nos da la probabilidad de $y$ dado $x$. Puede formularse de la siguiente manera:

La verosimilitud máxima intenta hacer que el numerador sea grande y el denominador pequeño para maximizar la probabilidad. Esto es equivalente a minimizar $-\log(P(Y \mid W))$ que se da a continuación

El gradiente de la funcion de pérdida de probabilidad logarítmica negativa para una muestra Y es el siguiente:

En el gradiente anterior, el primer término del gradiente en el punto de datos $Y$ y el segundo término del gradiente nos da el valor esperado del gradiente de la energía sobre todos los $Y$. Por lo tanto, cuando realizamos un descenso de gradiente, el primer término intenta reducir la energía dada al punto de datos $Y$ y el segundo término intenta aumentar la energía dada a todos los demás $Y$.

El gradiente de la función de energía es generalmente muy complejo y, por lo tanto, calcular, estimar o aproximar la integral es un caso muy interesante, ya que es intratable en la mayoría de los casos.

Modelo basado en energía de variable latente

La principal ventaja de los modelos de variables latentes es que permiten múltiples predicciones a través de la variable latente. Como $z$ varía en un conjunto, $y$ varía en la variedad de posibles predicciones. Algunos ejemplos incluyen:

1. K-medias
2. Modelado disperso
3. Optimización generativa de variables latentes Generative Latent Optimization(GLO)

Estos pueden ser de dos tipos:

1. Modelos condicionales donde $y$ depende de $x$
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. Modelos incondicionales que tienen una función de energía de valor escalar, $F(y)$ que mide la compatibilidad entre los componentes de $y$
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

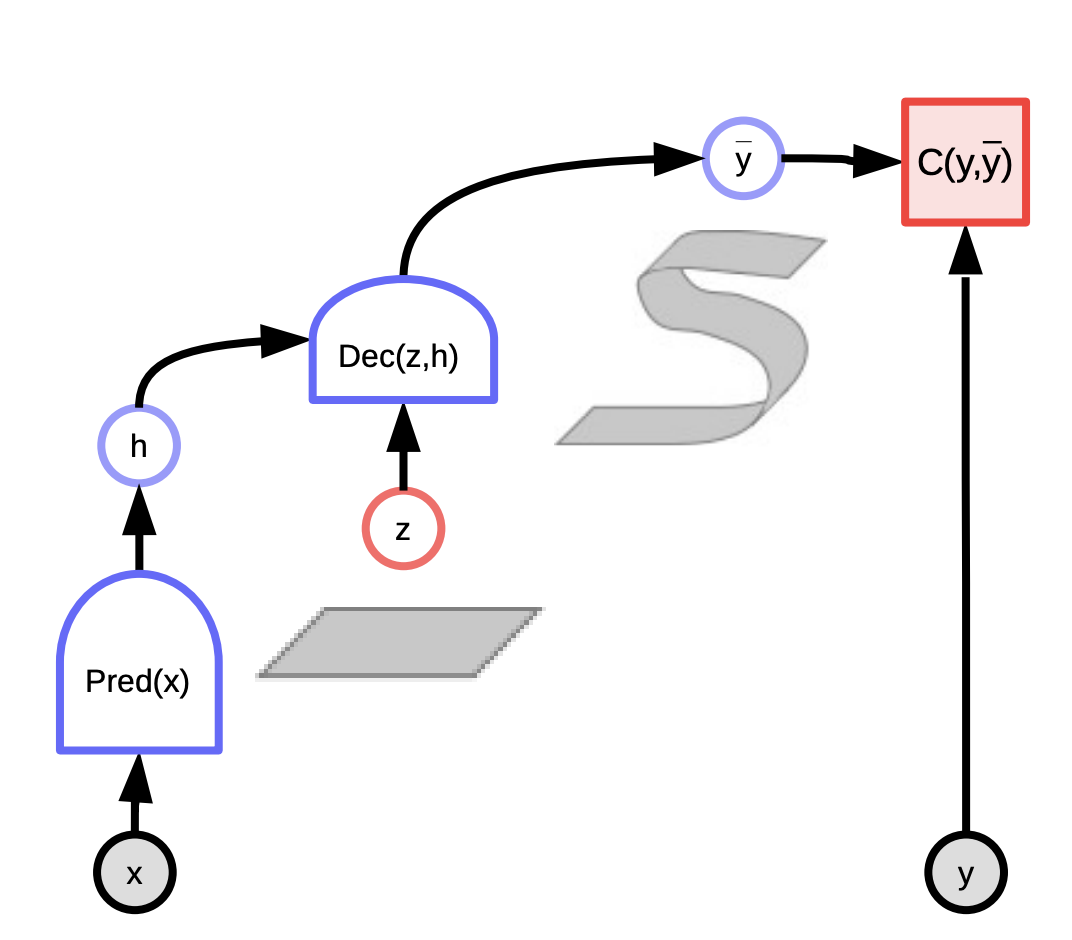
Fig. 3: EBM de variable latente

Ejemplo de EBM de variable latente: $K$-medias

K-medias es un algoritmo de agrupamiento simple que también se puede considerar como un modelo basado en energía donde estamos tratando de modelar la distribución sobre $y$. La función de energía es $E(y,z) = \Vert y-Wz \Vert^2$ donde $z$ es un vector $1$-hot.

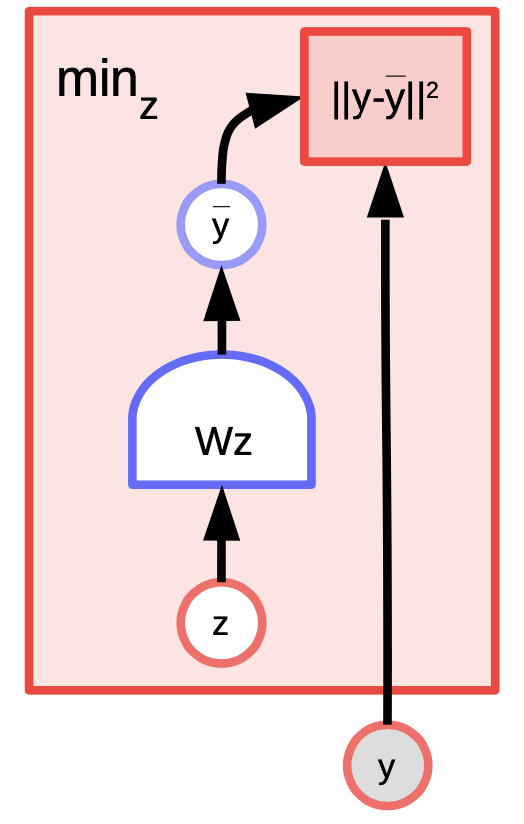
Fig. 4: Ejemplo de K-medias

Dado un valor de $y$ y $k$, podemos hacer inferencias calculando cuál de las $k$ posibles columnas de $W$ minimiza el error de reconstrucción o la función de energía. Para entrenar el algoritmo, podemos adoptar un enfoque en el que podemos encontrar $z$ para elegir la columna de $W$ más cercana a $y$ y luego intentar acercarnos aún más dando un paso de gradiente y repetir el proceso. Sin embargo, el descenso de gradiente coordinado en realidad funciona mejor y más rápido.

En el gráfico de abajo podemos ver los puntos de datos a lo largo de la espiral rosada. Las manchas negras que rodean esta línea corresponden a pozos cuadráticos alrededor de cada uno de los prototipos de $W$.

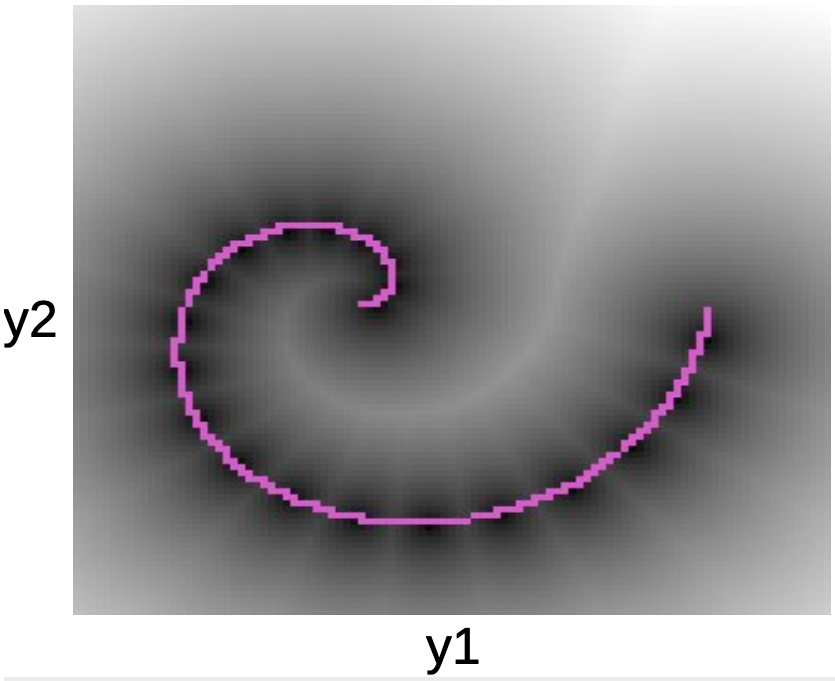
Fig. 5: Gráfico de espiral

Una vez que aprendamos la función de energía, podemos comenzar a abordar preguntas como:

1. Dado un punto $y_1$, ¿podemos predecir $y_2$?
2. Dado $y$, ¿podemos encontrar el punto más cercano en la variedad de datos?

K-medias pertenece a los métodos arquitectónicos (a diferencia de los métodos contrastivos). Por lo tanto, no empujamos hacia arriba la energía en ninguna parte, todo lo que hacemos es empujar la energía hacia abajo en ciertas regiones. Una desventaja es que una vez que se ha decidido el valor de $k$, solo puede haber $k$ puntos que tengan $0$ de energía, y todos los demás puntos tendrán una energía mayor que crecerá cuadráticamente a medida que nos alejamos de ellos.

Métodos contrastivos

Según el Dr. Yann LeCun, todos usarán métodos arquitectónicos en algún momento, pero en este momento, son los métodos contrastivos los que funcionan para imágenes. Considera la siguiente figura que nos muestra algunos puntos de datos y contornos de la superficie de energía. Idealmente, queremos que la energía de la superficie tenga la energía más baja en el variedad de datos. Por lo tanto, lo que nos gustaría hacer es reducir la energía (es decir, el valor de $F(x,y)$) alrededor del ejemplo de entrenamiento, pero esto por sí solo puede no ser suficiente. Por lo tanto, también lo aumentamos para los $y$ en la región que debería tener alta energía pero tiene baja energía.

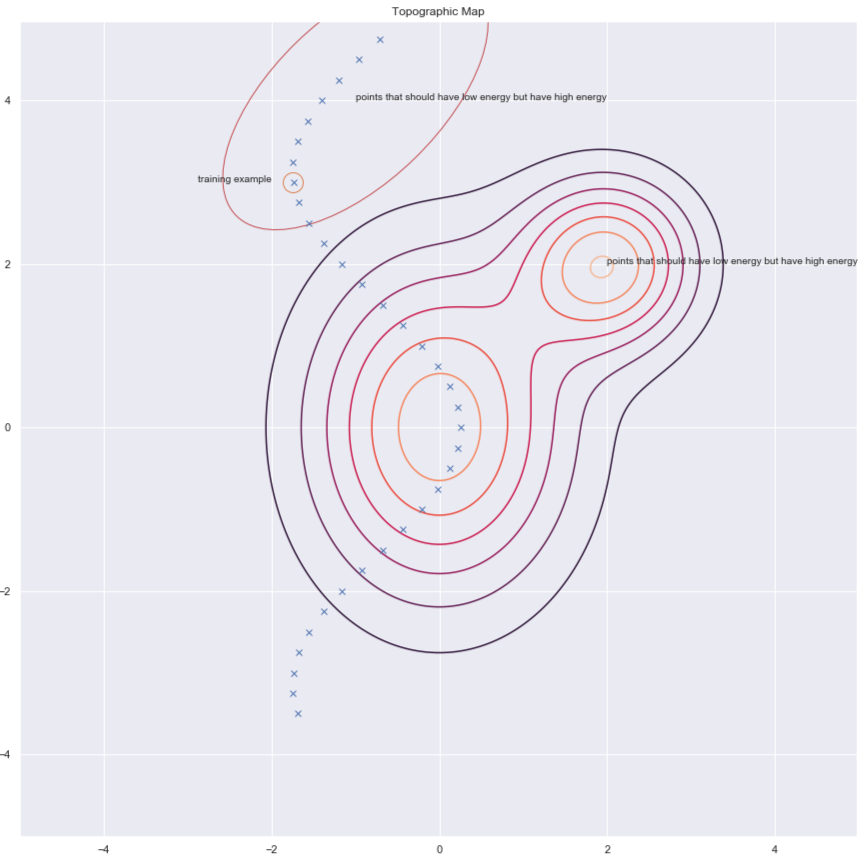
Fig. 6: Métodos contrastivos

Hay varias formas de encontrar estos $y$ candidatos para los que queremos aumentar la energía. Algunos ejemplos son:

1. Autoencoder Eliminador de Ruido
2. Divergencia contrastiva
3. Monte Carlo
4. Cadena de Markov Monte Carlo
5. Montecarlo Hamiltoniano

Discutiremos brevemente autoencoders eliminadores de ruido y la divergencia contrastiva.

Autoencoder Eliminador de Ruido (Denoising autoencoder, DAE)

Una forma de encontrar $y$ para aumentar la energía es perturbando aleatoriamente el ejemplo de entrenamiento como lo muestran las flechas verdes en la gráfica de abajo.

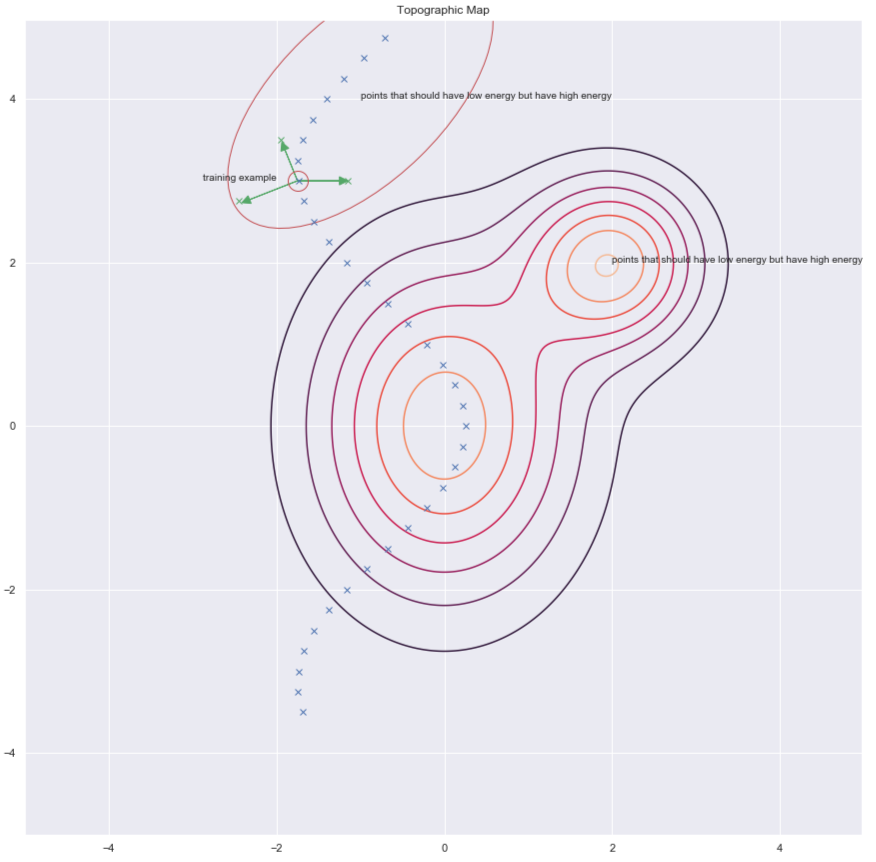
Fig. 7: Mapa topográfico

Una vez que tengamos un punto de datos dañado, podemos empujar la energía hacia arriba. Si hacemos esto suficientes veces para todos los puntos de datos, la muestra de energía se acumulará alrededor de los ejemplos de entrenamiento. El siguiente gráfico ilustra cómo se realiza el entrenamiento.

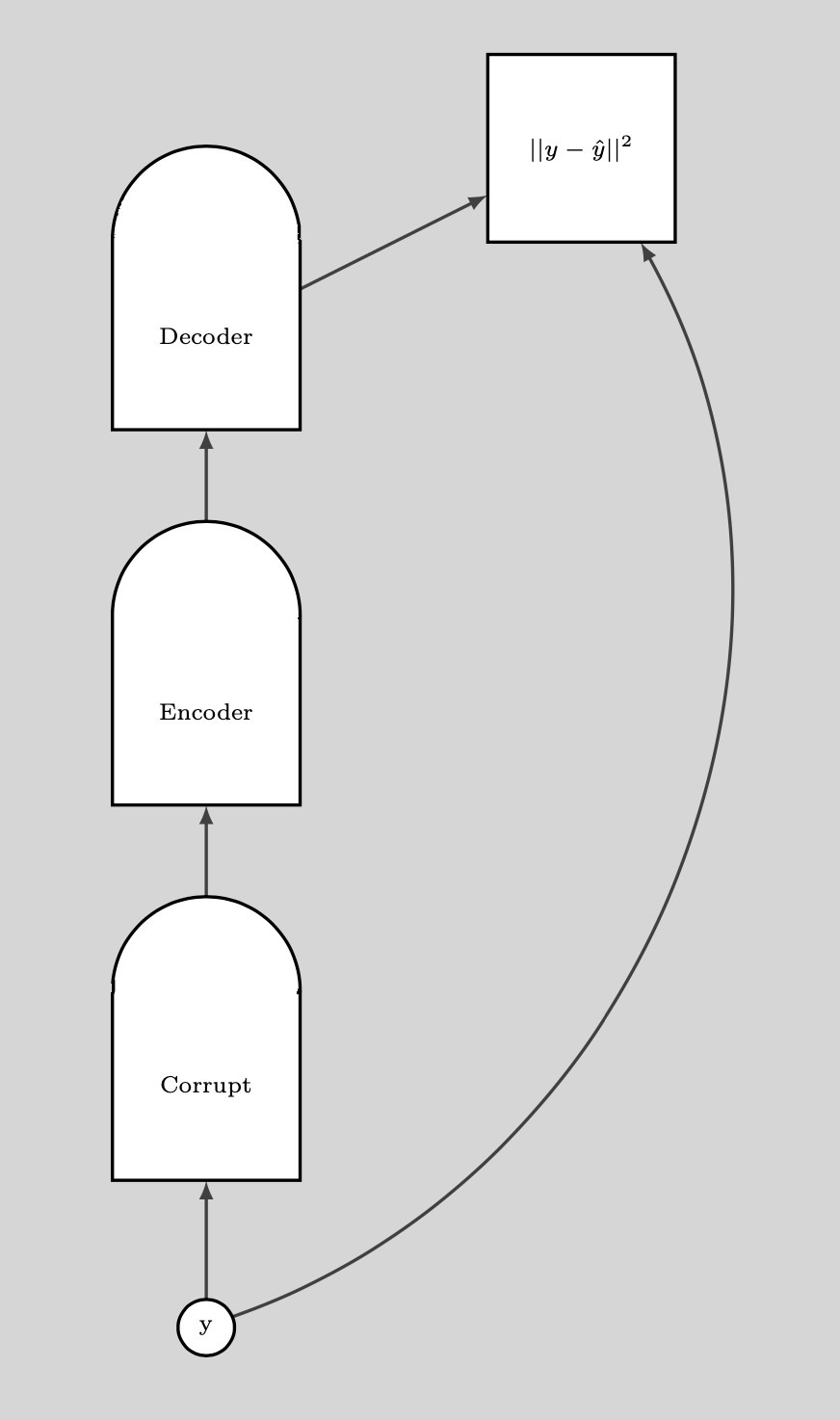
Fig. 8: Entrenamiento

Pasos para el entrenamiento:

1. Toma un punto $y$ y dañalo
2. Entrene el codificador y el decodificador para reconstruir el punto de datos original a partir de este punto de datos dañado.

Si el DAE está debidamente entrenado, la energía crece de forma cuadrática a medida que nos alejamos de la variedad de datos.

La siguiente gráfica ilustra cómo usamos el DAE.

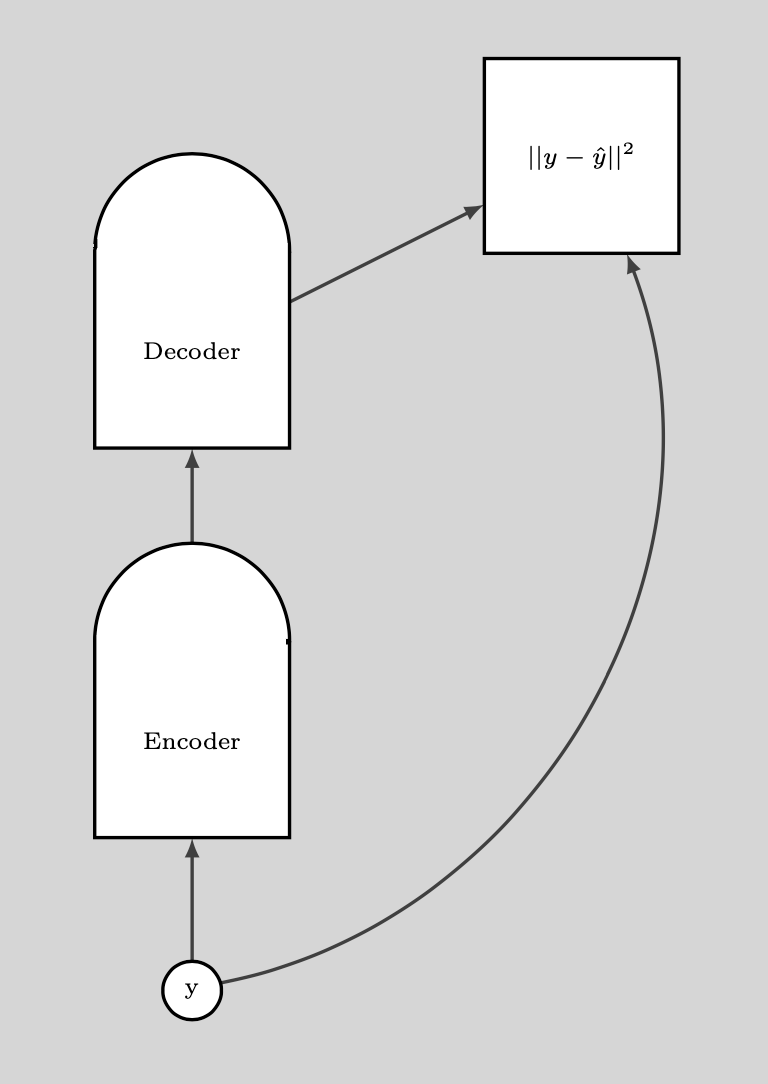
Fig. 9: Cómo se usa DAE

BERT

BERT se entrena de manera similar, excepto que el espacio es discreto ya que estamos tratando con texto. La técnica de dañar consiste en enmascarar algunas de las palabras y el paso de reconstrucción consiste en intentar predecirlas. Por lo tanto, a esto también se le llama un autoencoder enmascarado.

Divergencia contrastiva

La divergencia contrastiva nos presenta una forma más inteligente de encontrar el punto $y$ para el que queremos empujar la energía hacia arriba. Podemos dar una patada aleatoria a nuestro punto de entrenamiento y luego bajar la función de energía usando el descenso de gradiente. Al final de la trayectoria, aumentamos la energía para el punto en el que aterrizamos. Esto se ilustra en el gráfico siguiente utilizando la línea verde.

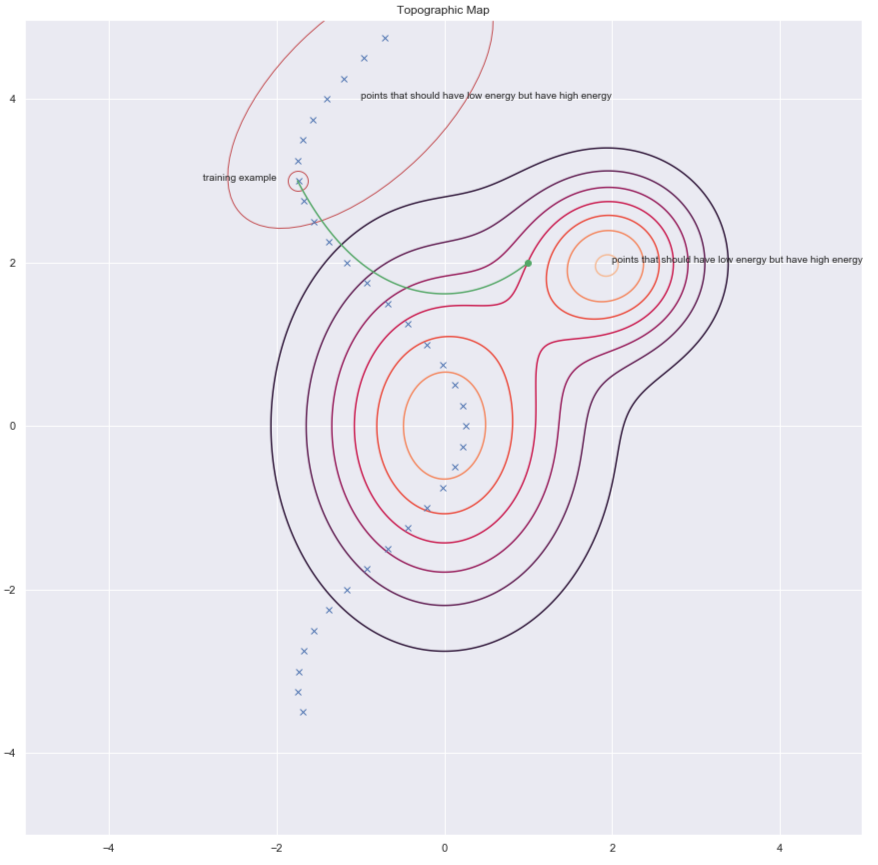
Fig. 10: Divergencia contrastiva