Modelos basados en energía (EBM)

Descripción general

Introduciremos una nueva estructura para definir modelos. Esta proporciona un marco unificador que ayuda a definir modelos supervisados, no supervisados y auto-supervisados. Los modelos basados en energía observan un conjunto de variables $x$ y generan un conjunto de variables $y$. Hay 2 problemas principales con las redes prealimentadas:

1. ¿Qué sucede si el procedimiento de inferencia es un cálculo más complejo que las capas apiladas de sumas ponderadas?
2. ¿Qué pasa si hay múltiples salidas posibles para una sola entrada? Ejemplo: predecir futuros fotogramas de video. Esencialmente en una red de clasificación, entrenamos esta red para emitir una puntuación para cada clase. Sin embargo, esto no es posible hacerlo en un dominio continuo de alta dimensión como imágenes. (¡No podemos tener softmax sobre imágenes!). Incluso si la salida es discreta, podría tener un gran espacio de muestra. Por ejemplo, el texto es compositivo que lleva a una gran cantidad de combinaciones posibles. Los modelos basados en energía proporcionan una mejor estructura para modelar estas modalidades.

Enfoque de EBM

En lugar de intentar clasificar $x$ en $y$, nos gustaría predecir si un determinado par de ($x$, $y$) encaja o no. O en otras palabras, encuentrar un $y$ compatible con $x$. También podemos plantear el problema como encontrar un $y$ para el cual algún $F(x,y)$ es bajo. Por ejemplo:

• ¿Es $y$ una imagen precisa de alta resolución de $x$?
• ¿Es el texto A una buena traducción del texto B?

Definición

Definimos una función de energía $F: \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$ donde $F(x,y)$ describe el nivel de dependencia entre pares $(x,y)$. (Nota que esta energía se usa en inferencia, no en el aprendizaje.) La inferencia esta dada por la siguiente ecuación:

Solución: inferencia basada en gradientes

Nos gustaría que la función de energía fuera suave y diferenciable para poder usarla para realizar el método de inferencia basado en gradientes. Para realizar inferencias, buscamos esta función usando el descenso de gradiente para encontrar $y$ compatibles. Hay muchos métodos alternativos a los métodos de gradiente para obtener el mínimo.

Aparte: Los modelos gráficos son un caso especial de modelos basados en energía. La función de energía se descompone como una suma de términos de energía. Cada término de energía tiene en cuenta un subconjunto de variables con las que estamos tratando. Si se organizan en una forma particular, existen algoritmos de inferencia eficientes para encontrar el mínimo de la suma de los términos con respecto a la variable que nos interesa inferir.

EBM con variables latentes

La salida $y$ depende de $x$, así como también de una variable adicional $z$ (la variable latente) cuyo valor no conocemos. Estas variables latentes pueden proporcionar información auxiliar. Por ejemplo, una variable latente puede indicarle las posiciones de los límites de las palabras en un fragmento de texto. Esto sería útil para saber cuándo queremos interpretar la escritura a mano sin espacios. Esto también es especialmente útil para saber en el habla que puede tener lagunas difíciles de descifrar. Adicionalmente, algunos idiomas tienen límites de palabras muy tenues (por ejemplo, francés). Por tanto, tener esta variable latente en nuestro modelo será muy útil para interpretar dicha entrada.

Inferencia

Para hacer inferencia con variable latente de EBM, queremos minimizar simultáneamente la función de energía con respecto a y and z.

Y esto equivale a redefinir la función energética como: \(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\), que equivale a: \(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z))\). Cuando $\beta \rightarrow \infty$, entonces $\check{y} = \text{argmin}_{y}F(x,y)$.

Otra gran ventaja de permitir variables latentes, es que al variar la variable latente sobre un conjunto, podemos hacer que la salida de predicción $y$ varíe también sobre la variedad de predicciones posibles (la cinta se muestra en el gráfico debajo): $F(x,y) = \text{argmin}_{z} E(x,y,z)$.

Esto permite que una máquina produzca múltiples salidas, no solo una.

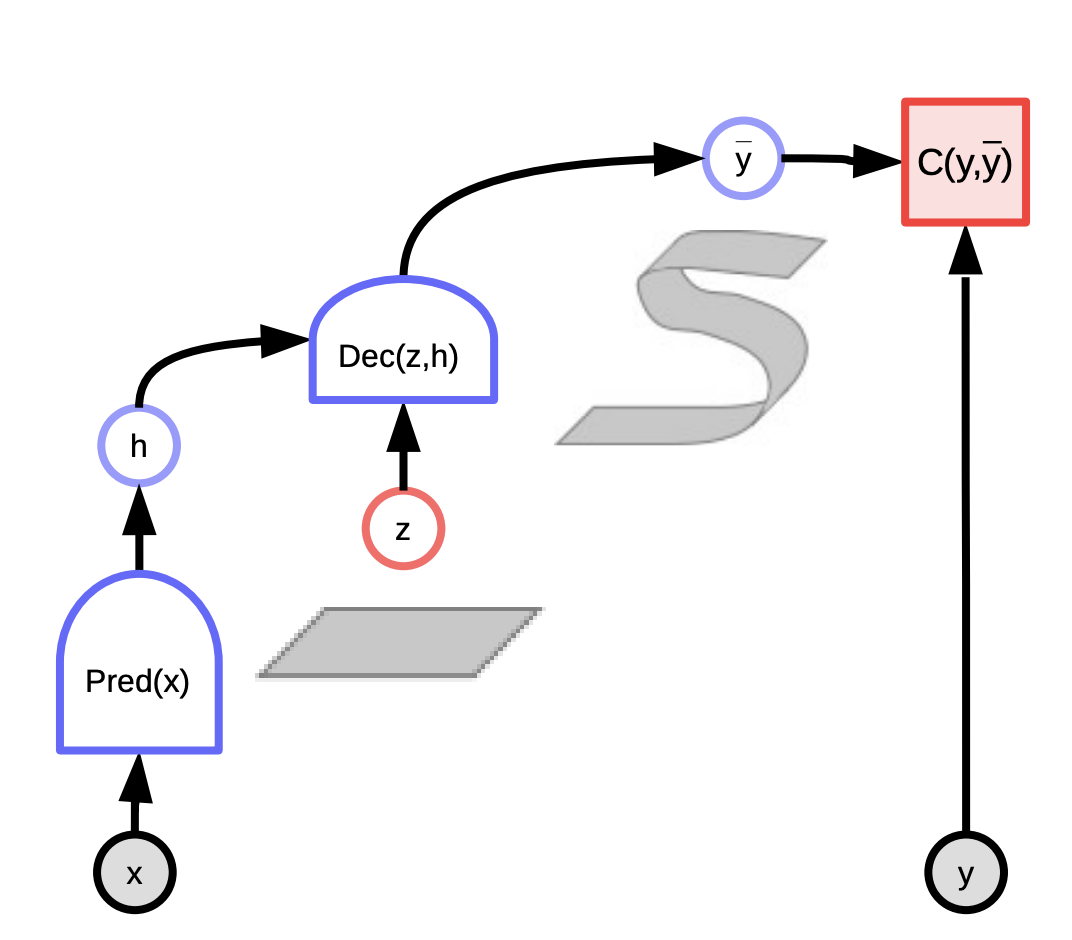
Fig. 1: Grafo computacional de modelos basados ​​en energía

Ejemplos

Un ejemplo es la predicción de video. Hay muchas buenas aplicaciones para que usemos la predicción de video, un ejemplo es hacer un sistema de compresión de video. Otra es usar un video tomado de un automóvil autónomo y predecir lo que harán otros automóviles.

Otro ejemplo es la traducción. La traducción de idiomas siempre ha sido un problema difícil porque no existe una única traducción correcta para un texto de un idioma a otro. Usualmente, hay muchas formas diferentes de expresar la misma idea y las personas encuentran difícil razonar por qué eligen una sobre la otra. Así que sería bueno si tuviéramos alguna forma de parametrizar todas las posibles traducciones que un sistema podría producir para responder a un texto dado. Digamos que si queremos traducir del alemán al inglés, podría haber varias traducciones en inglés que sean todas correctas y, al variar algunas variables latentes, puede variar la traducción producida.

Modelos basados en energía v.s. modelos probabilísticos

Podemos ver las energías como probabilidades logarítmicas negativas no normalizadas, y usar la distribución de Gibbs-Boltzmann para convertir de energía a probabilidad después de que la normalización sea:

donde $\beta$ es constante positiva y debe calibrarse para adaptarse a su modelo. Más grande $\beta$ da un modelo más fluctuante mientras más pequeño $\beta$ da un modelo más suave. (En física, $\beta$ es la temperatura inversa: $\beta \rightarrow \infty$ significa que la temperatura llega a cero).

Ahora, si se margina sobre y: $P(y \mid x) = \int_z P(y,z \mid x)$, tenemos:

Por lo tanto, si tenemos un modelo de variable latente y queremos eliminar la variable latente $z$ de una manera probabilísticamente correcta, solo necesitamos redefinir la función de energía $F_\beta$ (Energía libre)

Energía libre

Calcular esto puede ser muy difícil … De hecho, en la mayoría de los casos, probablemente sea intratable. Entonces, si tienes una variable latente que deseas minimizar dentro de su modelo, o si tienes una variable latente sobre la que desea marginar (lo que haces al definir esta función de energía $F$), y minimizar corresponde al límite infinito de $\beta$ de esta fórmula, entonces se puede hacer.

Según la definición de $F_\beta(x, y)$ anterior, $P(y \mid x)$ es solo una aplicación de la fórmula de Gibbs-Boltzmann y $z$ ha sido marginado implícitamente dentro de esto. Los físicos llaman a esto “Energía Libre”, por eso lo llamamos $F$. Entonces $e$ es la energía, y $F$ es la energía libre.

Pregunta: ¿Puedes explicar las ventajas que ofrecen los modelos basados en energía? En los modelos basados en probabilidad, también puedes tener variables latentes, que se pueden marginar.

La diferencia es que en los modelos probabilísticos, básicamente no tienes la opción de la función objetivo que vas a minimizar, y debe mantenerse fiel a la estructura probabilística en el sentido de que cada objeto que manipules tiene que ser una distribución normalizada (que puedes aproximar utilizando métodos variacionales, etc.). Aquí, estamos diciendo que, en última instancia, lo que quieres hacer con estos modelos es tomar decisiones. Si construyes un sistema que conduce un automóvil y el sistema te dice “Necesito girar a la izquierda con probabilidad de 0.8 o girar a la derecha con probabilidad de 0.2”, vas a girar a la izquierda. El hecho de que las probabilidades sean 0,2 y 0,8 no importa; lo que quieres es tomar la mejor decisión, porque estás obligado a tomar una decisión. De modo que las probabilidades son inútiles si quieres tomar decisiones. Si deseas combinar la salida de un sistema automatizado con otro (por ejemplo, un humano o algún otro sistema), y estos sistemas no se entrenaron juntos, sino que se entrenaron por separado, entonces lo que deseas son puntajes calibrados para que puedas combinar las puntuaciones de los dos sistemas para que puedas tomar una buena decisión. Solo hay una forma de calibrar los puntajes y es convertirlos en probabilidades. Todas las demás formas son inferiores o equivalentes. Pero si vas a entrenar un sistema de principio a fin para que tome decisiones, entonces cualquier función de puntuación que utilices está bien, siempre y cuando dé la mejor puntuación a la mejor decisión. Los modelos basados en energía te brindan muchas más opciones sobre cómo manejar el modelo, pueden tener más opciones sobre cómo entrenarlo y qué función objetivu utilizas. Si insiste en que su modelo sea probabilístico, debe usar la máxima verosimilitud; básicamente, debes entrenar tu modelo de tal manera que la probabilidad que le dé a los datos que observó sea máxima. El problema es que solo se puede probar que esto funciona en el caso de que tu modelo sea “correcto”, y tu modelo nunca es “correcto”. Hay una cita de un famoso estadístico [Goerge Box] que dice “Todos los modelos son incorrectos, pero algunos son útiles.” Entonces, los modelos probabilísticos, particularmente aquellos en espacios de alta dimensión y en espacios combinatorios como el texto, son todos modelos aproximados. Todos están mal de alguna manera, y si intentas normalizarlos, los haces más mal. Así que es mejor no normalizarlos.

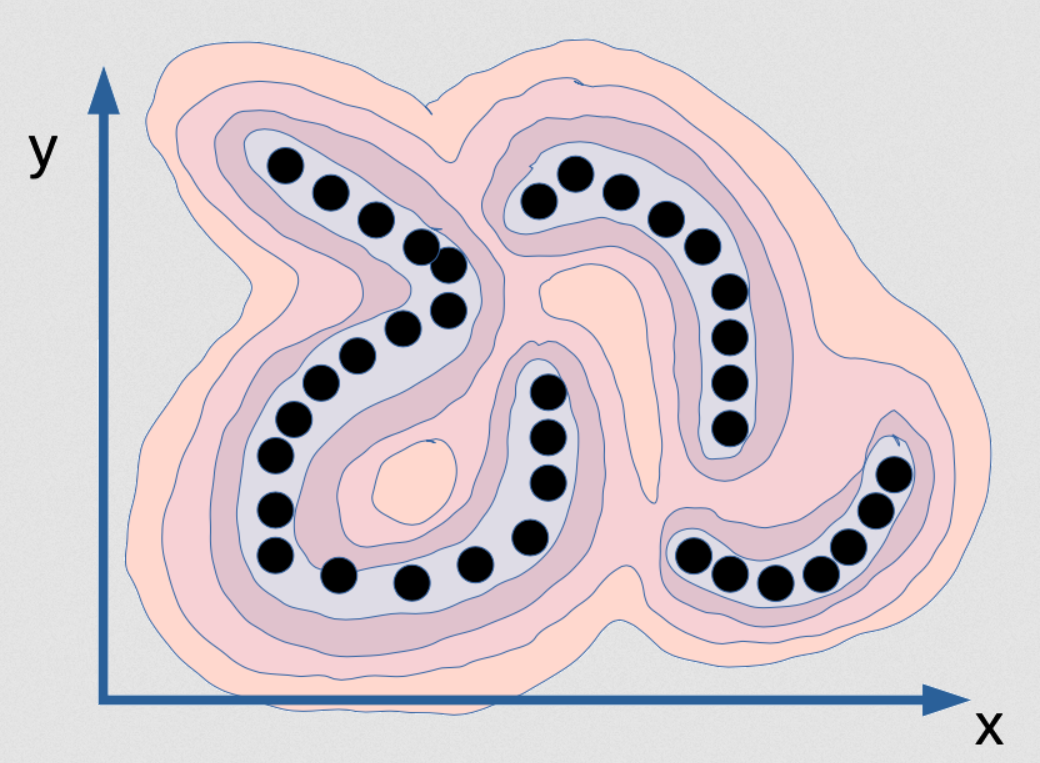
Fig. 2: Visualización de la función de energía que captura la dependencia entre x e y

Esta es una función de energía que está destinada a capturar la dependencia entre x e y. Es como una cordillera, por así decirlo. Los valles están donde están los puntos negros (estos son puntos de datos), y hay montañas alrededor. Ahora, si entrenas un modelo probabilístico con esto, imagina que los puntos están en realidad en una variedad topológica infinitamente delgada. Entonces, la distribución de datos para los puntos negros es en realidad solo una línea, y hay tres de ellos. En realidad, no tienen ancho. Entonces, si entrenas un modelo probabilístico en esto, su modelo de densidad debería indicarte cuándo se encuentra en esta variedad topológica. En esta variedad topológica, la densidad es infinita, y solo $\varepsilon$ fuera de ella debería ser cero. Ese sería el modelo correcto de esta distribución. No solo la densidad debe ser infinita, sino que la integral sobre [x e y] debe ser 1. ¡Esto es muy difícil de implementar en la computadora! No solo eso, sino que también es básicamente imposible. Supongamos que deseas calcular esta función a través de algún tipo de red neuronal; tu red neuronal tendrá que tener pesos infinitos, y deberán calibrarse de tal manera que la integral de la salida de ese sistema en todo el dominio es 1. Eso es básicamente imposible. El exacto y correcto modelo probabilístico para este ejemplo de datos en particular es imposible. Esto es lo que la máxima verosimilitud querrá que produzcas, y no hay computadora en el mundo que pueda calcular esto. Entonces, de hecho, ni siquiera es interesante. Imagina que tienes el modelo de densidad perfecto para este ejemplo, que es una placa delgada en ese espacio (x, y), ¡no puedes hacer inferencias! Si te doy un valor de x y te pregunto “¿cuál es el mejor valor de y?” No podrías encontrarlo porque todos los valores de y, excepto un conjunto de probabilidad cero, tienen una probabilidad de cero, y solo hay unos pocos valores que son posibles. Para estos valores de x por ejemplo:

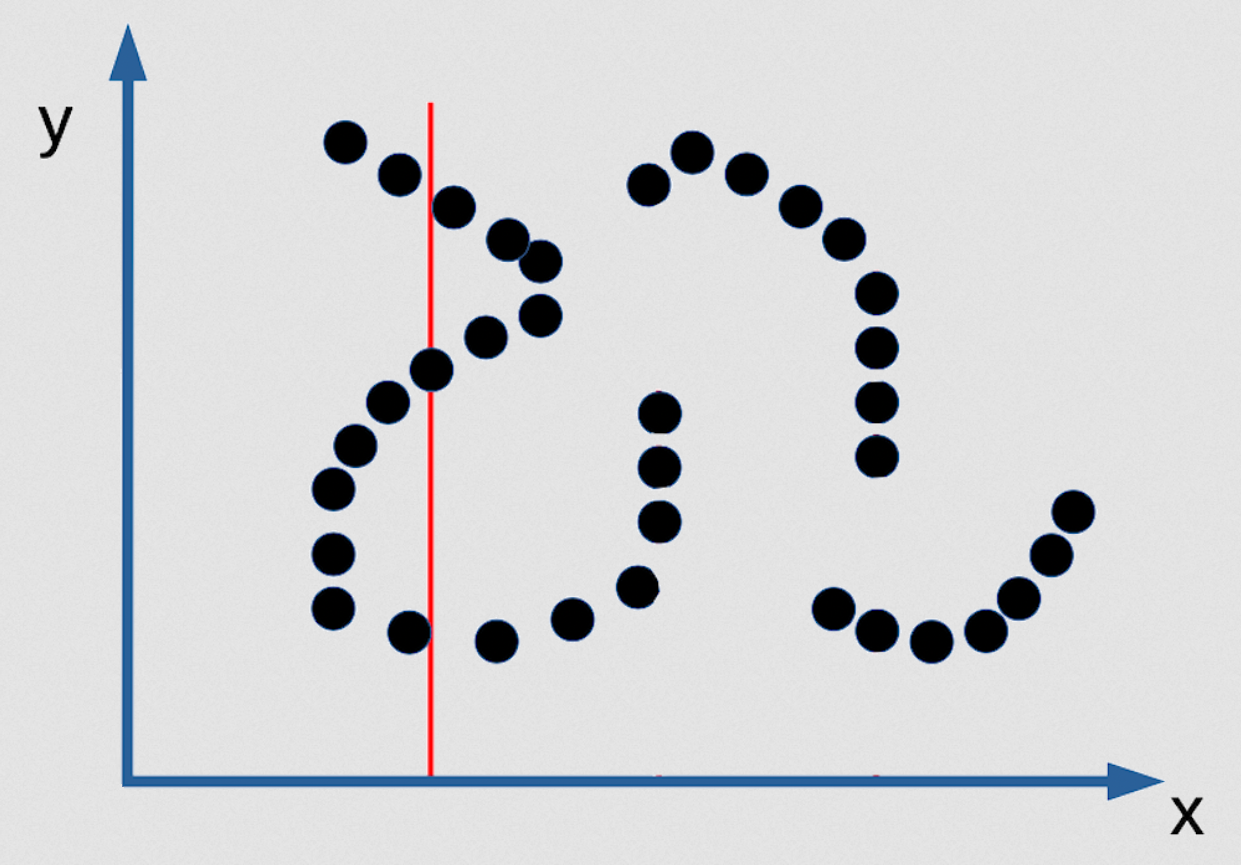
Fig. 3: Ejemplo de predicción múltiple de EBM como función implícita

Hay 3 valores de y que son posibles y son infinitamente estrechos. Entonces no podrías encontrarlos. No existe un algoritmo de inferencia que te permita encontrarlos. La única forma en que puedas encontrarlos es si haces que tu función de contraste sea suave y diferenciable, y luego puedes comenzar desde cualquier punto y, mediante el descenso de gradiente, puedes encontrar un buen valor para y para cualquier valor de x. Pero este no va a ser un buen modelo probabilístico de la distribución si la distribución es del tipo que mencioné. Así que aquí hay un caso en el que insistir en tener un buen modelo probabilístico es realmente malo. ¡La máxima verosimilitud apesta [en este caso]!

Entonces, si eres un verdadero bayesiano, dices “oh, pero puedes corregir esto teniendo una probabilidad a priori fuerte donde la probabilidad a priori dice que tu función de densidad tiene que ser suave”. Podrías pensar en esto como una probabilidad a priori. Pero, todo lo que haces en términos bayesianos (toma el logaritmo del mismo, olvídate de la normalización) obtienes modelos basados en energía. Los modelos basados en energía que tienen un regularizador, que es aditivo a tu función de energía, son completamente equivalentes a los modelos bayesianos donde la probabilidad es exponencial de la energía, y ahora obtienes $\exp(\text{energy}) \exp(\text{regulariser})$, por lo que es igual a $\exp(\text{energy} + \text{regulariser})$. Y si eliminas el exponencial, tienes un modelo basado en energía con un regularizador aditivo.

Por lo tanto, existe una correspondencia entre los métodos probabilístico y bayesiano, pero insistir en que hacer la máxima verosimilitud a veces es malo para usted, particularmente en espacios de alta dimensión o espacios combinatorios donde su modelo probabilístico es muy incorrecto. No está muy mal en distribuciones discretas (está bien) pero en casos continuos, puede estar realmente mal. Y todos los modelos están equivocados.