Arquitectura de las RNNs y modelos LSTM

Descripción general

Una RNN (Recurrent Neural Network) es un tipo de arquitectura que podemos usar para manejar secuencias de datos. ¿Qué es una secuencia? De la lección de CNNs, aprendimos que una señal puede ser 1D, 2D o 3D dependiendo del dominio. El dominio se define como desde donde estamos mapeando y hacia qué. El manejo de datos secuenciales se trata básicamente de datos 1D ya que el dominio es solo entradas temporales de X. Sin embargo, también se puede usar RNNs para tratar datos 2D, donde se tienen dos direcciones.

NNs simples vs. NNs recurrentes

A continuación se muestra un diagrama de red neuronal simple (vanilla) con tres capas. “Vainilla” es un término estadounidense que significa simple. La burbuja rosada es el vector de entrada x, en el centro está la capa oculta en verde, y la capa azul final es la salida. Usando un ejemplo de la electrónica digital a la derecha, esto es como compuerta lógica combinacional, donde la corriente de salida solo depende de la corriente de entrada.

Figura 1: Arquitectura Simple

A diferencia de una red neuronal simple, en las redes neuronales recurrentes la salida actual depende no solo de la entrada actual, sino también del estado del sistema, que se muestra a la izquierda de la imagen de arriba. Esto es como una compuerta lógica secuencial en electrónica digital, donde la salida también depende de un “flip-flop” (una unidad de memoria básica en electrónica digital). Por lo tanto, la principal diferencia aquí es que la salida de una red neuronal simple solo depende de la entrada actual, mientras que la de una RNN también depende del estado del sistema.

Figura 2: Arquitectura de una RNN

El diagrama de Yann agrega estas figuras entre las neuronas para representar el mapeo entre un tensor y otro (de un vector a otro). Por ejemplo, en el diagrama anterior, el vector de entrada x viajará a través de este elemento adicional a las representaciones ocultas h. Este elemento es en realidad una transformación afín, es decir, rotación más distorsión. Luego, a través de otra transformación, pasamos de la capa oculta a la salida final. Del mismo modo, en el diagrama de la RNN, se pueden tener los mismos elementos adicionales entre las neuronas.

Figura 3: Arquitectura de una RNN de Yann

Cuatro tipos de Arquitecturas de RNNs y algunos ejemplos

El primer caso es de una arquitectura del tipo vector a secuencia. La entrada será el círculo rosa y luego habrá evoluciones del estado interno del sistema representados como burbujas verdes. A medida que evoluciona el estado del sistema, para cada paso de tiempo habrá una salida específica, representada en azul.

Figura 4: Arquitectura 1: Vec a Sec

Un ejemplo de este tipo de arquitectura es tener una entrada de tipo imagen, mientras que la salida será una secuencia de palabras que representan las descripciones en español de la imagen de entrada. Haciendo uso del diagrama anterior, cada burbuja azul puede ser un índice en un diccionario de palabras en español. Por ejemplo, si la salida es la oración “Este es un autobús escolar amarillo”. Primero se obtiene el índice de la palabra “Esto”, luego el índice de la palabra “es” y así sucesivamente. Algunos de los resultados de esta red se muestran a continuación. Por ejemplo, en la primera columna, la descripción de la última imagen es “Una manada de elefantes caminando por un campo de hierba seca”, la cual está muy bien refinada. Luego, en la segunda columna, la primera imagen muestra “Dos perros juegan en la hierba”, cuando en realidad son tres perros. En la última columna están los ejemplos más equivocados, como “Un autobús escolar amarillo estacionado en un estacionamiento”. En general, estos resultados muestran que esta red puede fallar drásticamente y a veces funciona bien. Este es el caso de un vector de entrada, que es la representación de una imagen, a una secuencia de símbolos, que son, por ejemplo, caracteres o palabras que forman las oraciones en inglés. Este tipo de arquitectura se llama red autorregresiva. Una red autorregresiva es una red que proporciona una salida a partir de que se alimenta como entrada la salida anterior.

El segundo tipo de arquitectura es de secuencia a un vector final (secuencia a vector). Esta red se va alimentando con una secuencia de símbolos y solo al terminar devuelve un resultado final. Una aplicación de esto puede ser usar la red para interpretar Python. Por ejemplo, la entrada son estas líneas del programa Python.

Figura 5: Arquitectura 2: Sec a Vec

Entonces la red podrá generar la solución correcta a este programa. Otro programa más complicado puede ser este:

Figura 6: Arquitectura 2: Sec a Vec

En la que la salida debería ser 12184. Estos dos ejemplos muestran que se puede entrenar una red neuronal para hacer este tipo de operación. Solo necesitamos alimentarla con una secuencia de símbolos y hacer que la salida final sea un valor específico.

El tercer tipo de arquitectura es secuencia a vector a secuencia. Esta arquitectura solía ser la forma estándar de realizar traducción de idiomas. Se comienza con una secuencia de símbolos que se muestran aquí en rosa. Entonces todo se condensa en esta h final, que representa un concepto. Por ejemplo, podemos tener una oración como entrada y comprimirla temporalmente en un vector, que representa el significado y el mensaje que se debe enviar. Luego, después de obtener este significado en cualquier representación, la red lo desenrolla en un idioma diferente. Por ejemplo, “Hoy estoy muy feliz” como secuencia de palabras en español se puede traducir al italiano o al chino. En general, la red obtiene algún tipo de codificación como entradas y las convierte en una representación comprimida. Finalmente, realiza la decodificación dada la misma versión comprimida. En los últimos tiempos, se ha observado que redes como Transformers, que cubriremos en la próxima lección, superan este método en las tareas de traducción de idiomas. Este tipo de arquitectura solía ser tecnología de punta (SOTA) hace unos dos años (2018).

Si se realiza un PCA sobre el espacio latente, se obtendrán las palabras agrupadas por semántica como se muestra en este gráfico.

Figura 7: Arquitectura 3: Sec a Vec to Sec

Si hacemos zoom, veremos que en una misma ubicación se encuentran todos los meses, como enero y noviembre.

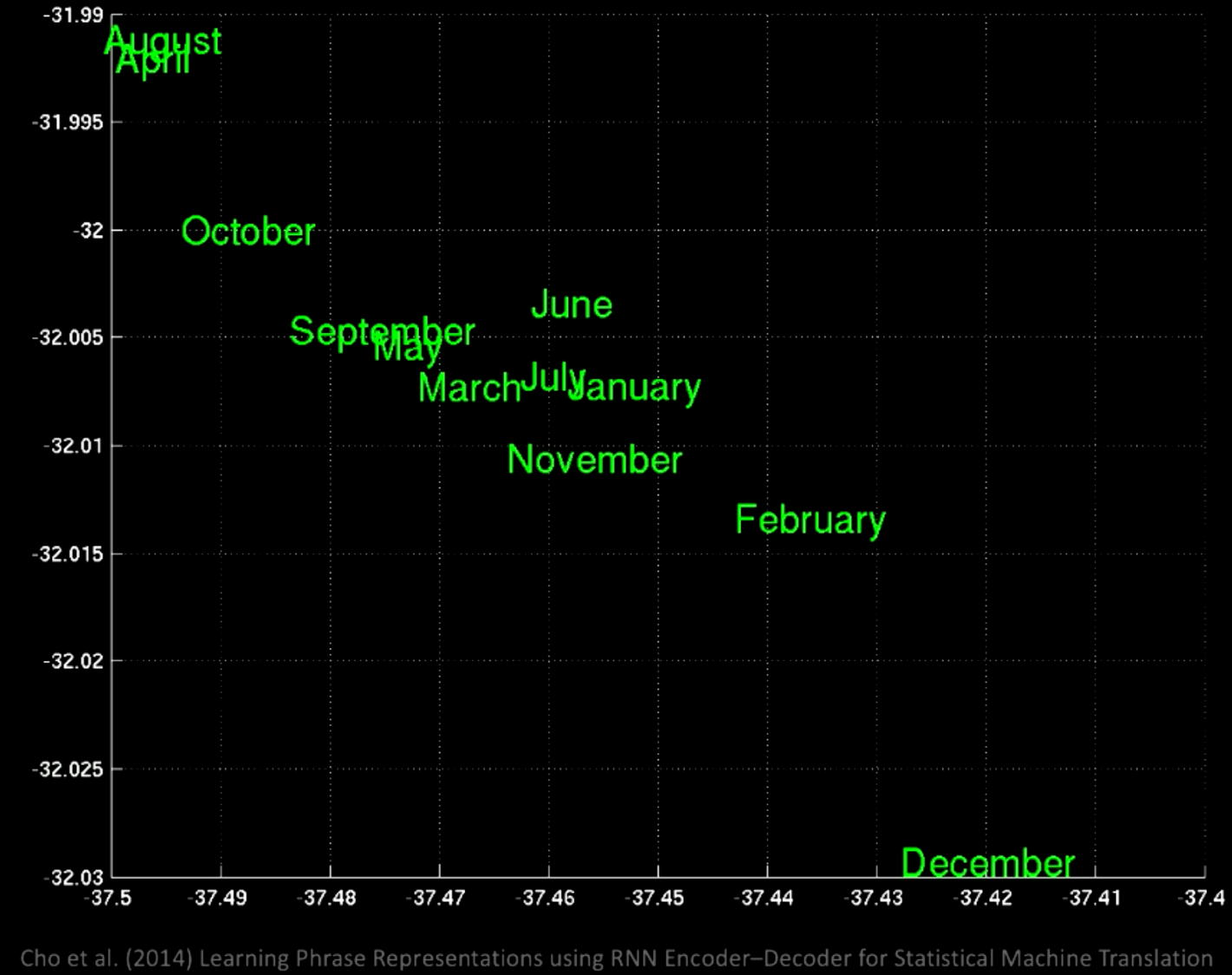
Figura 8: Arquitectura 3: Sec a Vec a Sec

Al enfocarse en una región diferente, se obtienen frases como “hace unos días”, “los próximos meses”, etc.

Figura 9: Arquitectura 3: Sec a Vec a Sec

A partir de estos ejemplos, vemos que diferentes ubicaciones tendrán algunos significados comunes específicos.

El cuarto y último caso es secuencia a secuencia. En esta red, a medida que se comienza a alimentar la entrada, la red comienza a generar salidas. Un ejemplo de este tipo de arquitectura es T9, que si recuerdas haber usado un teléfono Nokia, recibirías sugerencias de texto mientras escribías. Otro ejemplo es conversión de audio hablado a subtítulos. Un buen ejemplo es este escritor RNN. Cuando se comienza a escribir “los anillos de Saturno brillaron mientras”, sugiere lo siguiente “dos hombres se miraron”. Esta red fue entrenada sobre algunas novelas de ciencia ficción para que al escribir algo genere sugerencias que ayuden a escribir un libro. Un ejemplo más se muestra a continuación. Se ingresa algo en el indicador superior y luego esta red intentará completar el resto.

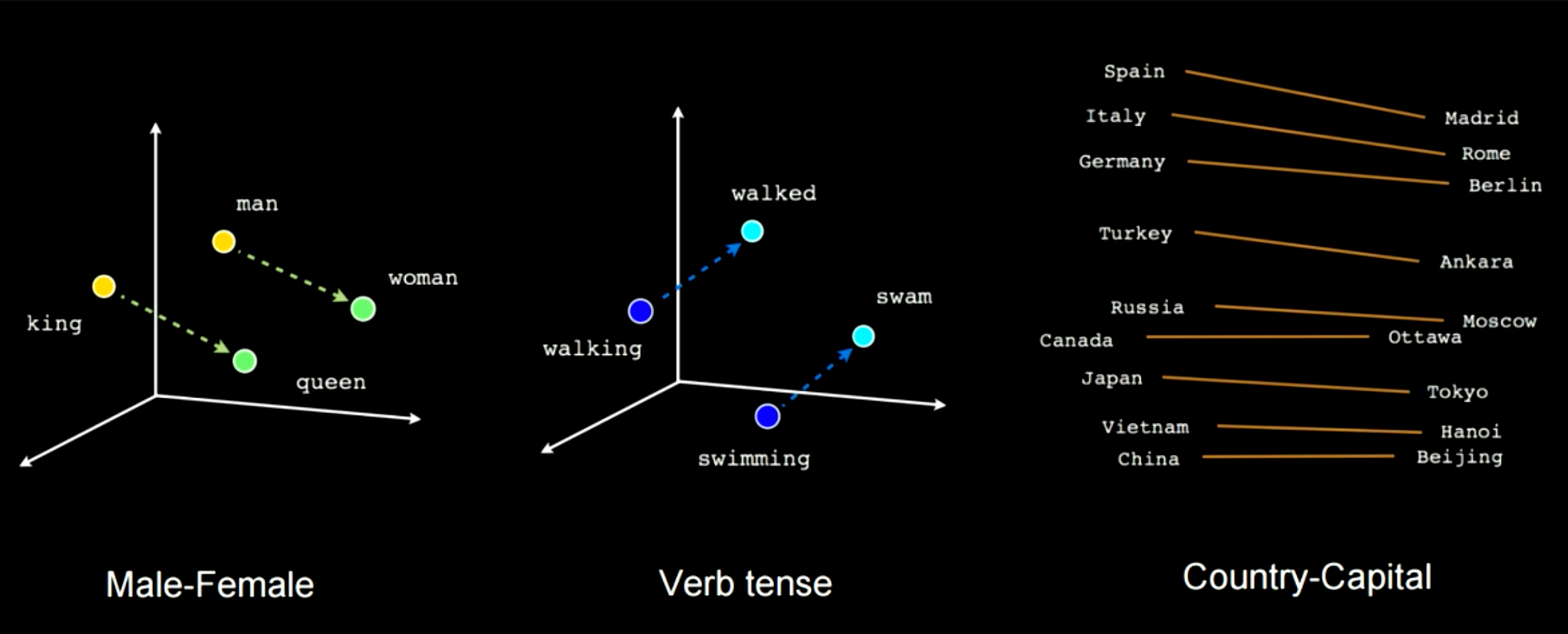
Figura 10: Arquitectura 4: Sec a Sec

Propagación Hacia Atrás a través del tiempo

Arquitectura del modelo

Para entrenar a un RNN, se debe utilizar la propagación hacia atrás a través del tiempo (BPTT). La arquitectura del modelo de RNN se muestra en la figura a continuación. El diseño de la izquierda utiliza la representación de bucle, mientras que la figura derecha despliega o desenrolla el bucle en una fila a lo largo del tiempo.

Figura 11: Propagación Hacia Atrás a través del tiempo

Las representaciones ocultas se declaran como

La primera ecuación indica una función no lineal aplicada a una rotación sobre una versión de entrada apilada, donde se agrega la configuración previa de la capa oculta. Al principio, $h[0]$ se establece como 0. Para simplificar la ecuación, $W_h$ se puede escribir como dos matrices separadas, $\left[ W_{hx}\ W_{hh} \right]$, por lo que a veces la transformación se expresa como

que corresponde a la representación apilada de la entrada.

$y[t]$ se calcula en la rotación final y luego podemos usar la regla de la cadena para propagar el error al paso de tiempo anterior.

Batch-Ificación en modelado de idiomas

Cuando se trata de una secuencia de símbolos, podemos separar el texto en batches de diferentes tamaños. Por ejemplo, cuando se trata de secuencias que se muestran en la siguiente figura, se aplica primero la separación en lotes, donde el dominio del tiempo se conserva verticalmente. En este caso, el tamaño del batch se establece en 4.

Figura 12: Batch-Ificación

Si el período $T$ de BPTT se establece en 3, la primera entrada $x[1:T]$ y la salida $y[1:T]$ para RNNs se determina como

Para procesar el primer lote a través de la RNN, en primer lugar, introducimos $x[1] = [a\ g\ m\ s]$ en la RNN y forzamos la salida a ser $y[1] = [b\ h\ n\ t]$. La representación oculta $h[1]$ se enviará al siguiente paso para ayudar a la RNN a predecir $y[2]$ a partir de $x[2]$. Después de enviar $h[T-1]$ al conjunto final de $x[T]$ e $y[T]$, cortamos el proceso de propagación de gradiente para $h[T]$ y $h[0]$, para que los gradientes no se propaguen infinitamente (.detach() en Pytorch). El proceso completo se muestra en la figura a continuación.

Figura 13: Batch-Ificación

Desvanecimiento y Explosión de Gradiente

Problema

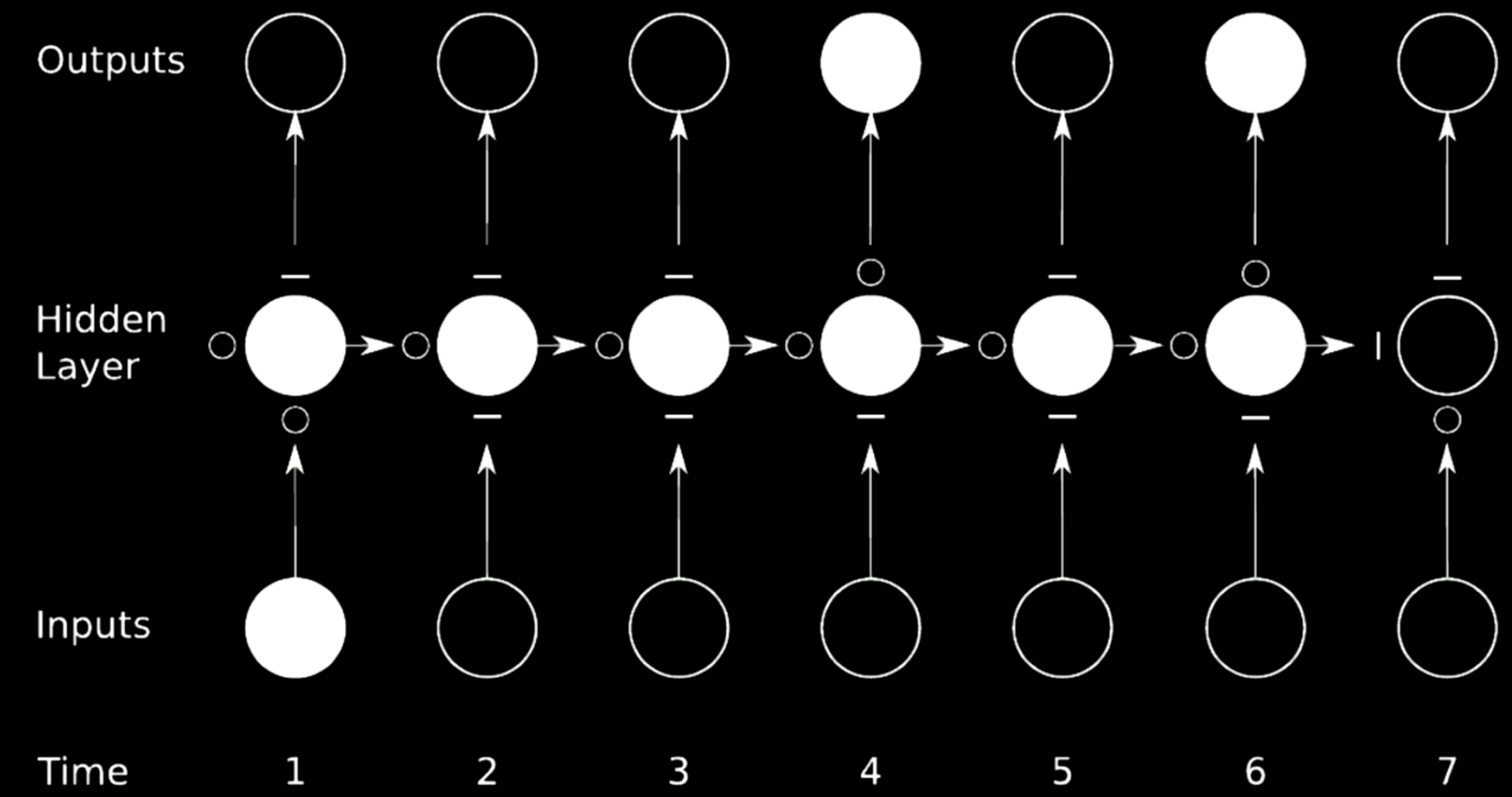
Figura 14:Problema del Desvanecimiento

La figura anterior es una arquitectura típica de RNN. Para realizar la operación de rotación sobre los pasos anteriores en RNNs, utilizamos matrices, que pueden considerarse flechas horizontales en el modelo anterior. Dado que las matrices pueden cambiar el tamaño de las salidas, si el determinante de ellas es mayor que 1, el gradiente se inflará con el tiempo y causará una explosión de gradiente. En términos relativos, si el autovalor o valor propio que seleccionamos es pequeño y cercano a 0, el proceso de propagación reducirá los gradientes y producirá el desvanecimiento del gradiente.

En las RNNs típicas, los gradientes se propagarán a través de todas las flechas posibles, lo que brinda a los gradientes una gran oportunidad de desaparecer o explotar. Por ejemplo, el gradiente en el tiempo 1 es grande, indicado con color más claro. Cuando pasa por una rotación, el gradiente se encoge mucho y en el paso temporal 3, se reduce a cero y muere.

Solución

Una estrategia ideal para evitar que los gradientes exploten o desaparezcan, es evitar o saltarse las conexiones. Para lograr ésto, se pueden usar redes de multiplicación.

Figura 15: Saltar conexiones

En el caso anterior, dividimos la red original en 4 redes. Comencemos por la primera red. Toma un valor de la entrada en el tiempo 1 y envía la salida al primer estado intermedio en la capa oculta. El estado tiene otras 3 redes donde los “$\circ$”s permiten que los gradientes pasen mientras que los “$-$”s bloquean la propagación. Dicha técnica se llama red recurrente con compuertas (Gated RNN).

LSTM (Long Short-Term Memory: Memoria Prolongada de Corto Plazo) es un tipo frecuente de RNN con compuertas y se presenta en detalle en las siguientes secciones.

Long Short-Term Memory

Arquitectura del Modelo

A continuación hay ecuaciones que expresan una LSTM. La compuerta de entrada se resalta con cuadros amarillos, que será una transformación afín. Esta transformación de entrada multiplicará $c[t]$, que es nuestra compuerta candidata.

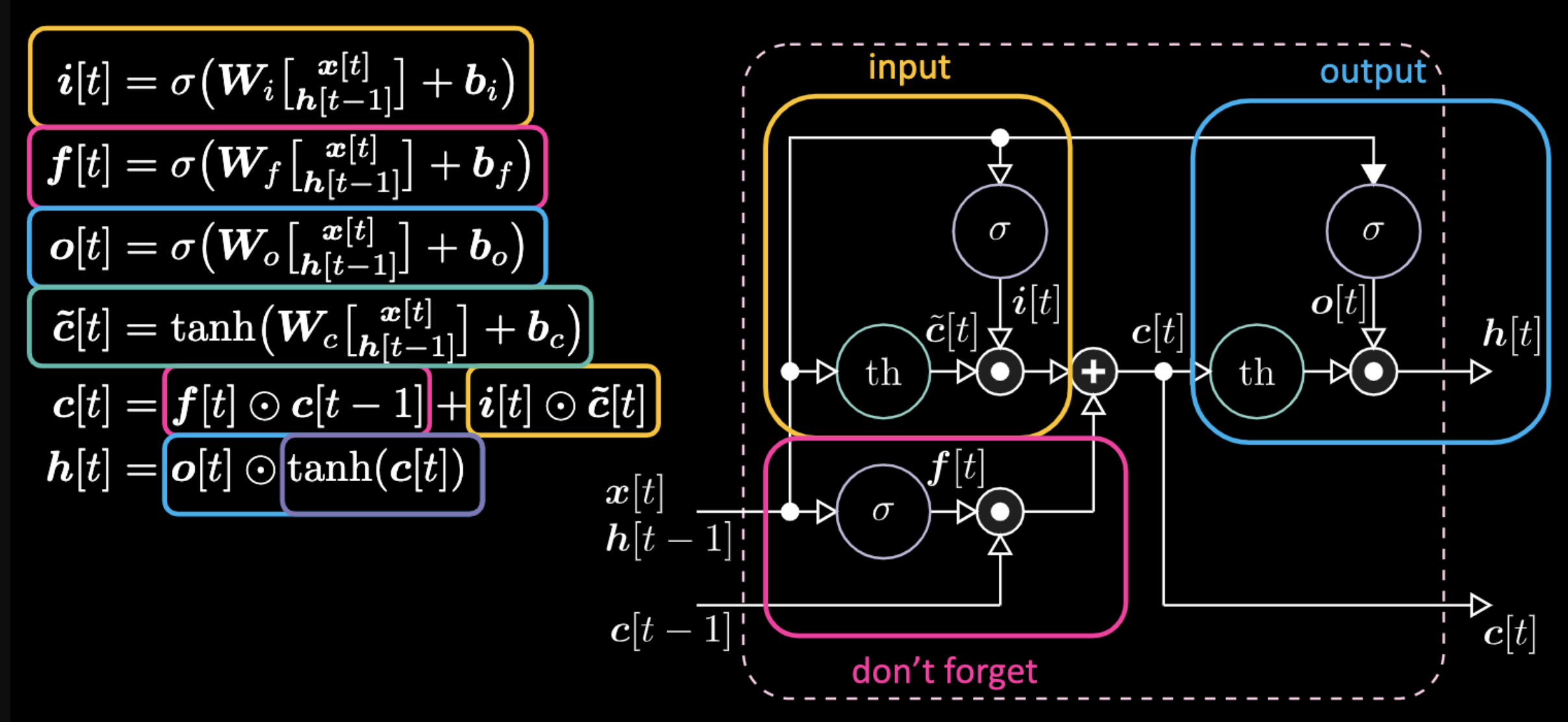
Figura 16: Arquitectura LSTM

La compuerta “no-olvidar” $f$ (don’t forget) está multiplicando el valor anterior de la celda de memoria $c[t-1]$. El valor total de la celda $c[t]$ es el de la compuerta no-olvidar más el de la compuerta de entrada. La representación oculta final es la multiplicación elemento a elemento entre la compuerta de salida $o[t]$ y la tangente hiperbólica aplicada a la celda $c[t]$, de modo que los límites superior e inferior estén acotados. Finalmente, la compuerta candidata $\tilde{c}[t]$ es simplemente una red recurrente. Entonces tenemos una $o[t]$ para modular la salida, una $f[t]$ para modular la compuerta de no olvidar y una $i[t]$ para modular la compuerta de entrada. Todas estas interacciones entre la memoria y las compuertas son interacciones multiplicativas. $i[t]$, $f[t]$ y $o[t]$ son todas funciones sigmoides, que van de cero a uno. Por lo tanto, cuando se multiplica por cero, se tiene una compuerta cerrada. Al multiplicar por uno, se obtiene una compuerta abierta.

¿Cómo apagamos la salida? Digamos que tenemos una representación interna púrpura $th$ y ponemos un cero en la compuerta de salida. Entonces la salida será cero multiplicado por algo, con lo que obtenemos un cero. Si ponemos un uno en la compuerta de salida, obtendremos el mismo valor que la representación púrpura.

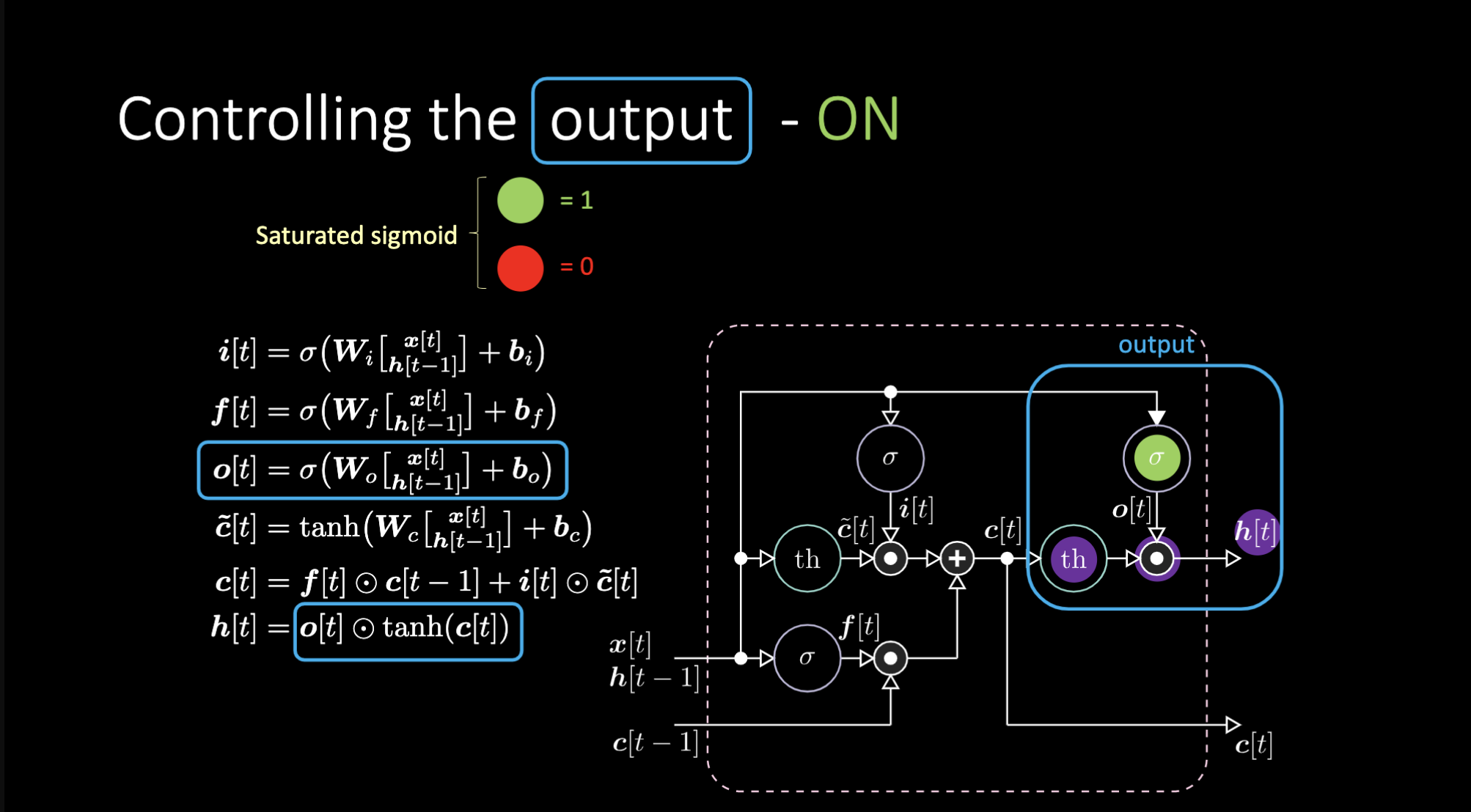
Figura 17: Arquitectura LSTM - Salida Activada

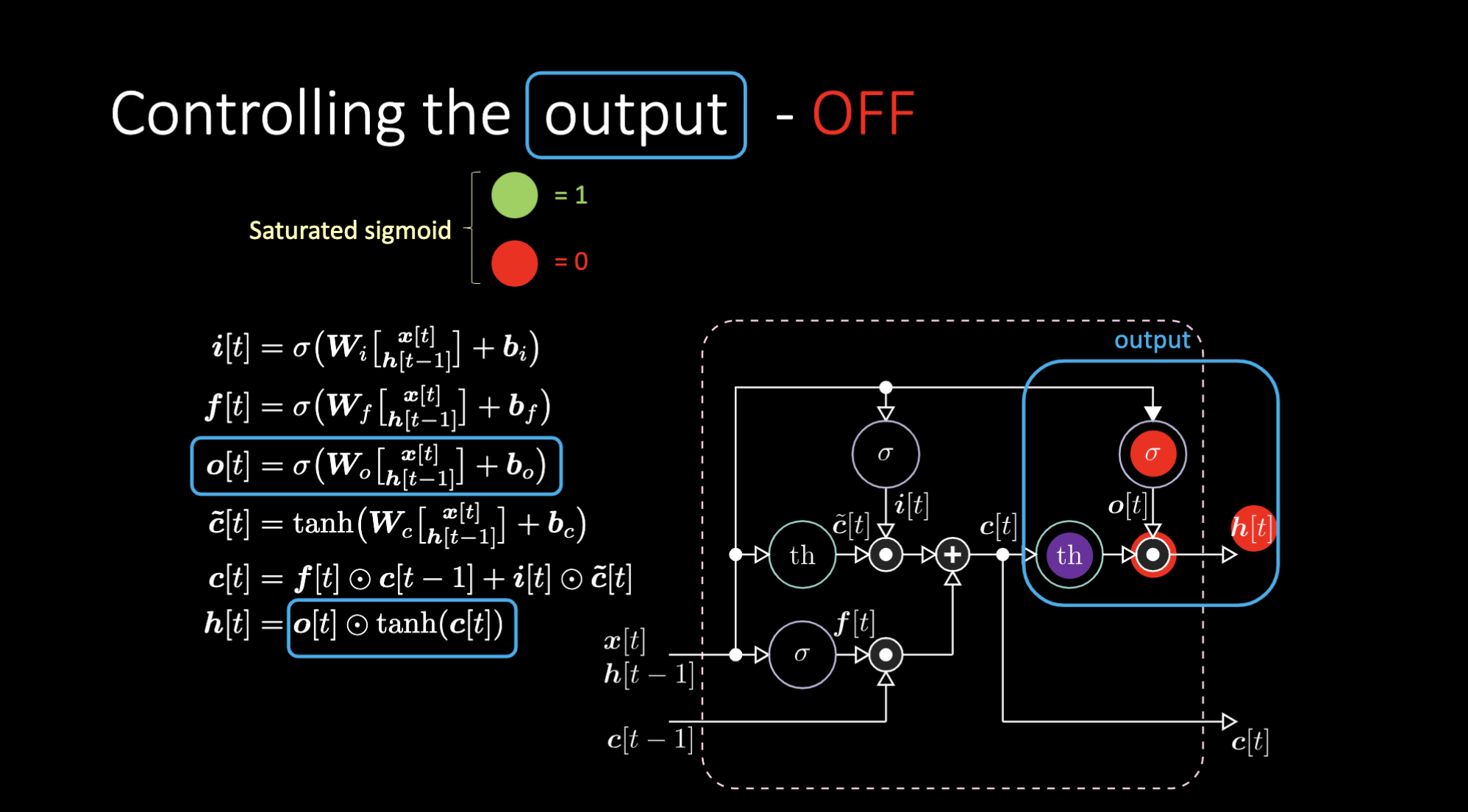
Figura 18: Arquitectura LSTM - Salida Desactivada

Del mismo modo podemos controlar la celda de memoria. Por ejemplo, podemos reiniciarla haciendo que $f[t]$ e $i[t]$ sean ceros. Después de la multiplicación y la suma, tendremos un cero dentro de la memoria. De lo contrario, podemos mantener la memoria, aún teniendo un cero en la representación interna $th$, pero manteniendo un uno en $f[t]$. Por lo tanto, la suma resulta en $c[t-1]$ y sigue su camino. Finalmente, podemos escribir, para lo cual debemos obtener un uno en la puerta de entrada, con lo que la multiplicación se vuelve púrpura, y luego establecer un cero en la compuerta de no olvidar para que realmente se olvide.

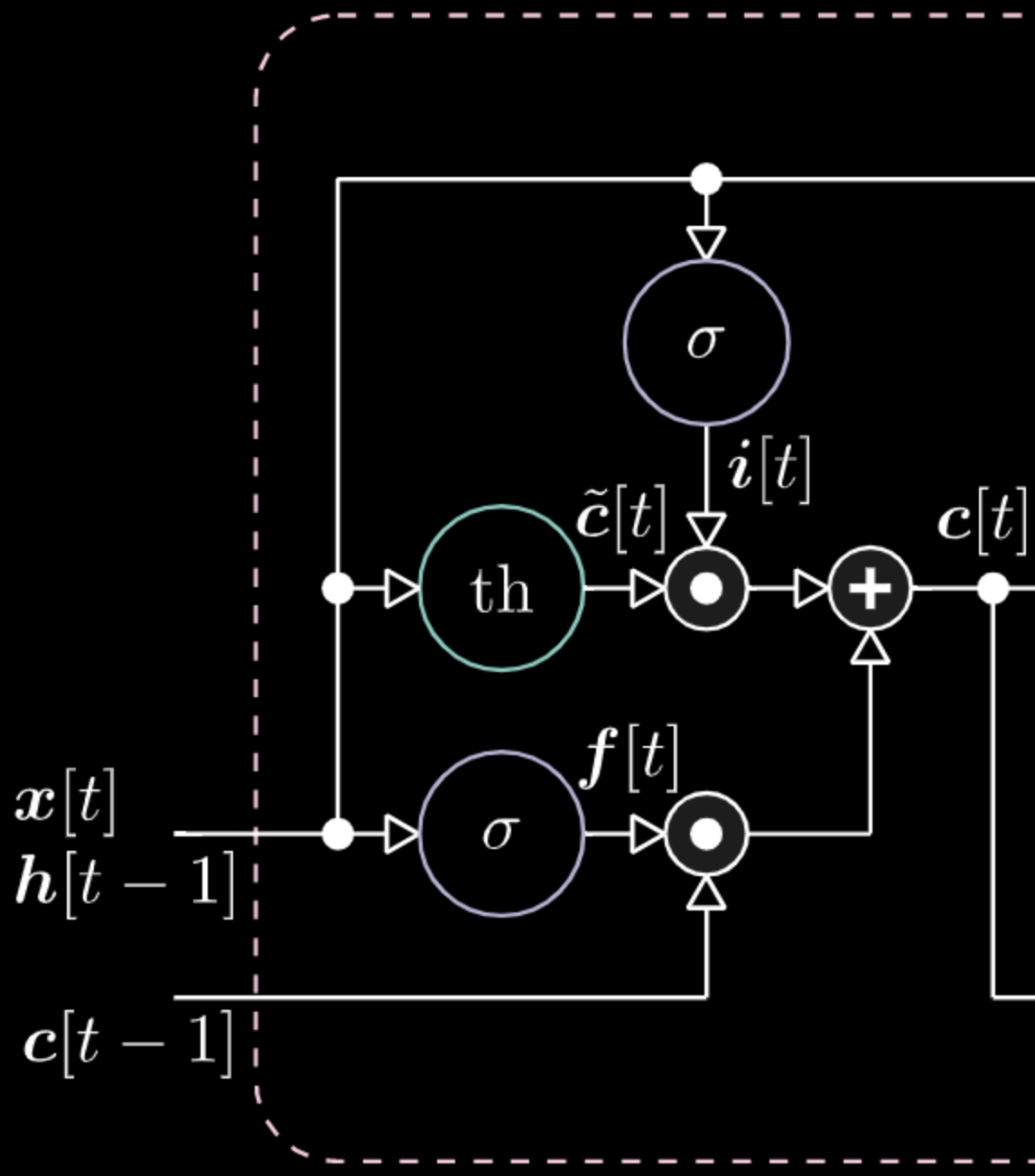
Figure 19: Visualización de la Celda de Memoria

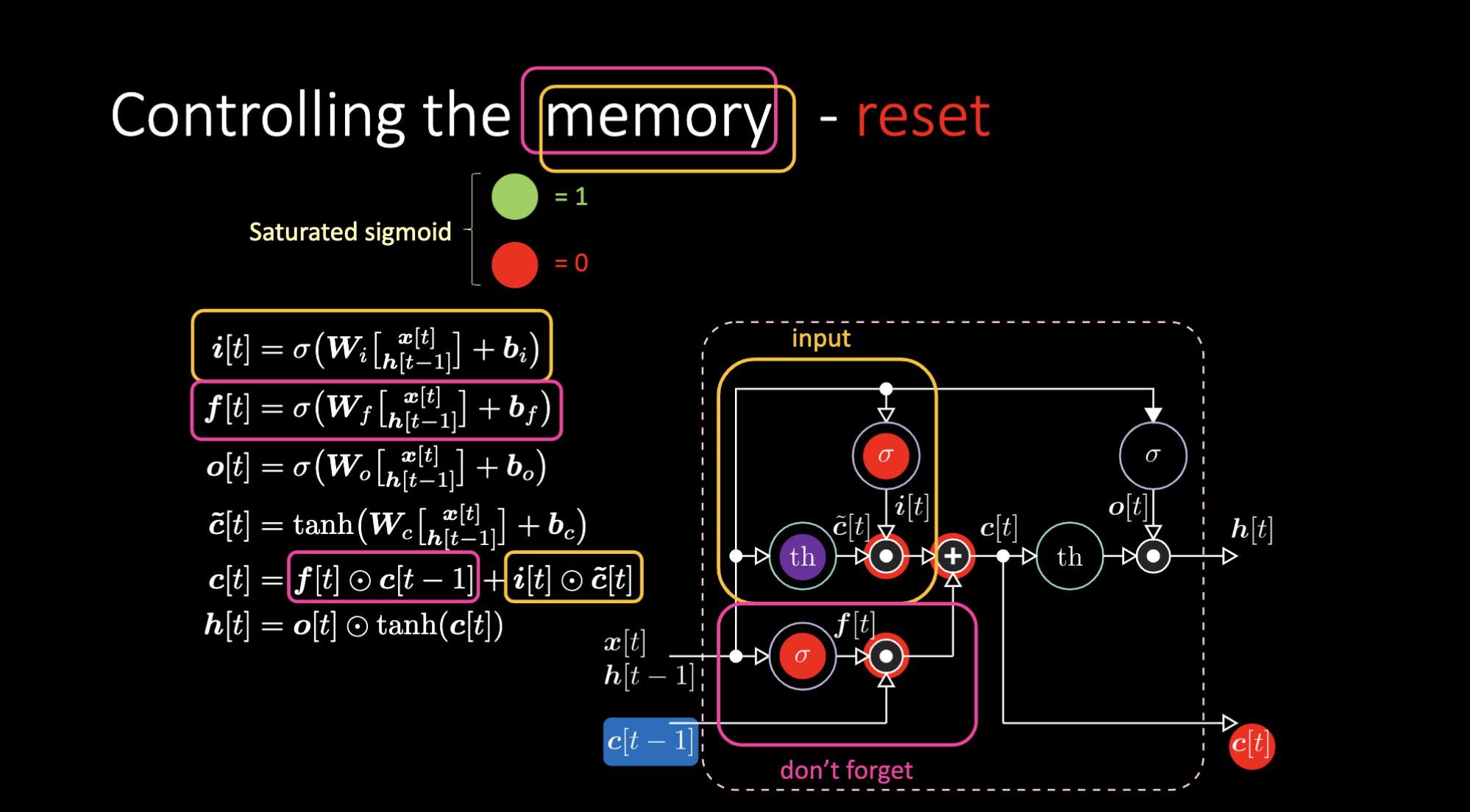
Figura 20: Arquitectura LSTM - Reinicio de Memoria

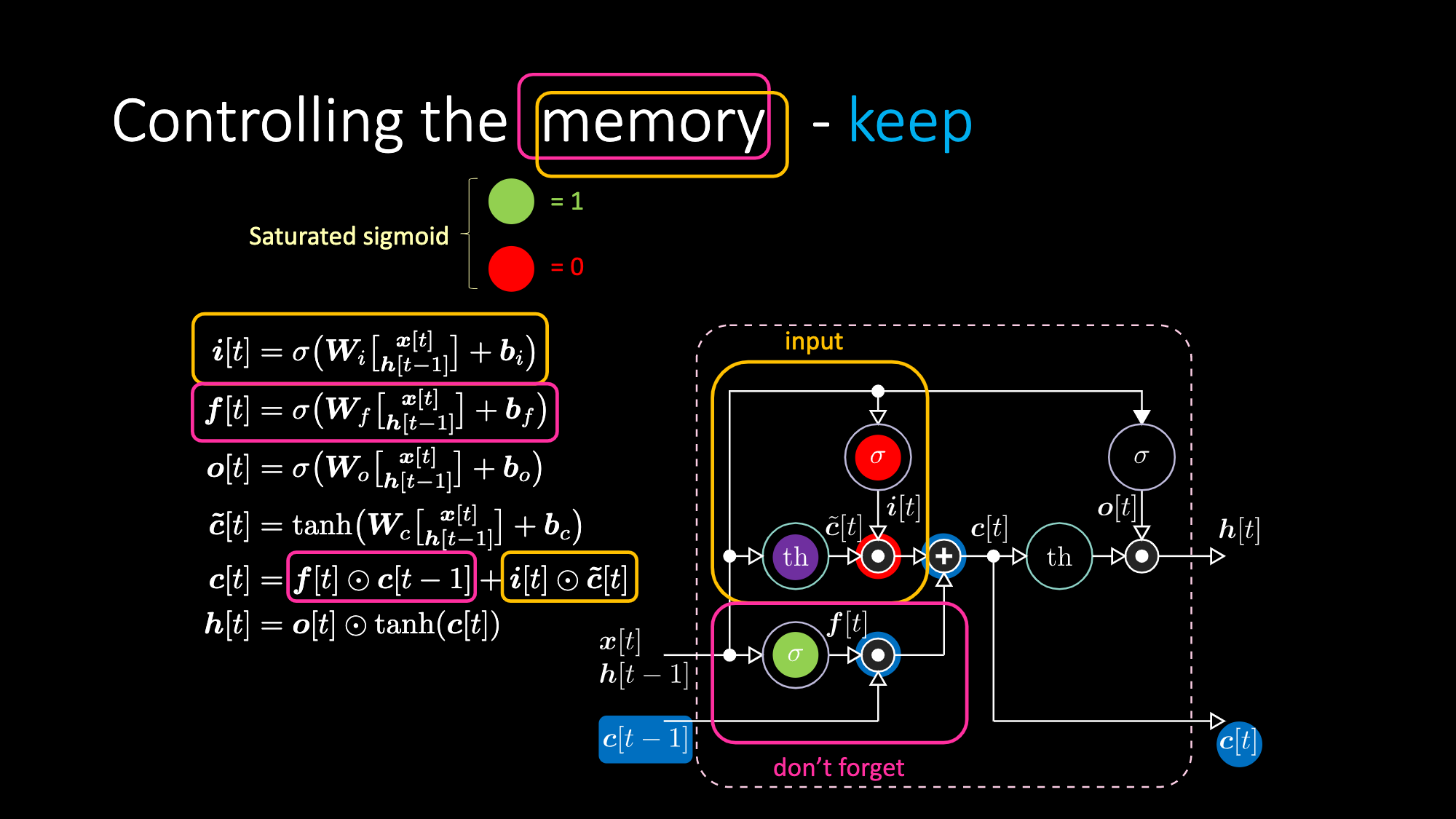
Figura 21: Arquitectura LSTM - Mantener Memoria

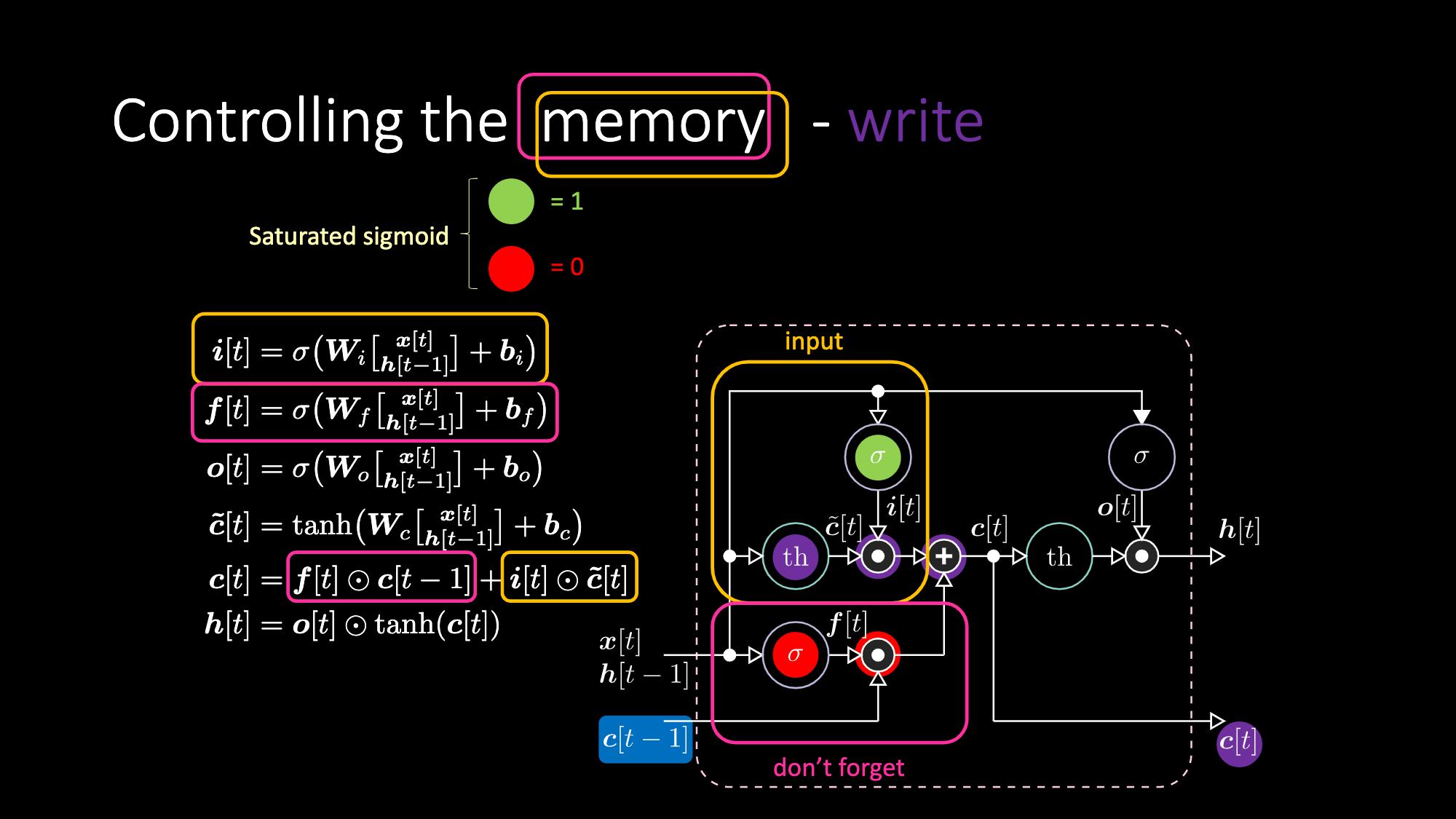
Figura 22: Architectura LSTM - Escribir Memoria

Ejemplos en Jupyter Notebook

Clasificación de Secuencias

El objetivo es clasificar secuencias. Los elementos y objetivos se representan localmente (vectores de entrada con un solo bit distinto de cero). La secuencia comienza (b**egins) con una B, termina (e**nds) con una E (el “símbolo de activación”), y de lo contrario consiste en símbolos elegidos al azar del conjunto {a, b, c , d} excepto por dos elementos en las posiciones $t_1$ y $t_2$ que son X o Y. Para el caso DifficultyLevel.HARD, la longitud de la secuencia se elige aleatoriamente entre 100 y 110, $t_1$ se elige aleatoriamente entre 10 y 20, y $t_2$ se elige aleatoriamente entre 50 y 60. Hay 4 clases de secuencia: Q, R, S y U, que dependen del orden temporal de X e Y. Las reglas son: X, X -> Q; X, Y -> R; Y, X -> S; Y, Y -> U.

1). Exploración de conjunto de datos

El tipo de retorno de un generador de datos es una tupla con longitud 2. El primer elemento de la tupla es el batch de secuencias con forma $(32, 9, 8)$. Estos son los datos que se enviarán a la red. Hay ocho símbolos diferentes en cada fila (X, Y, a, b, c, d, B, E). Cada fila es un vector one-hot. Una secuencia de filas representa una secuencia de símbolos. La primera fila de todos ceros es de relleno (padding). Usamos relleno cuando la longitud de la secuencia es más corta que la longitud máxima del batch. El segundo elemento en la tupla es el batch de etiquetas de clase correspondientes con forma $(32, 4)$, ya que tenemos 4 clases (Q, R, S y U). La primera secuencia es: BbXcXcbE. Entonces su etiqueta de clase decodificada es $[1, 0, 0, 0]$, correspondiente a Q.

Figura 23: Ejemplo de Vector de Entrada

2). Definiendo el Modelo y Entrenamiento

Creemos una red recurrente simple, una LSTM, y entrenemos durante 10 epochs. En el ciclo de entrenamiento, siempre debemos respetar cinco pasos:

• Realizar el pasaje hacia adelante del modelo
• Calcular el error (loss)
• Reiniciar a cero el caché de gradientes
• Propagar hacia atrás para calcular la derivada parcial del error con respecto a los parámetros
• Dar un pequeño paso en la dirección opuesta a la del gradiente

Figura 24: RNN Simple vs LSTM - 10 Epochs

Con un nivel de dificultad fácil, la RNN obtiene un 50% de precisión mientras que la LSTM obtiene un 100% después de 10 epochs. Pero la LSTM tiene cuatro veces más parámetros que la RNN y también tiene dos capas ocultas, por lo que no es una comparación justa. Después de 100 epochs, la RNN también obtiene un 100% de precisión, lo que muestra que se tarda más en entrenarla que a una LSTM.

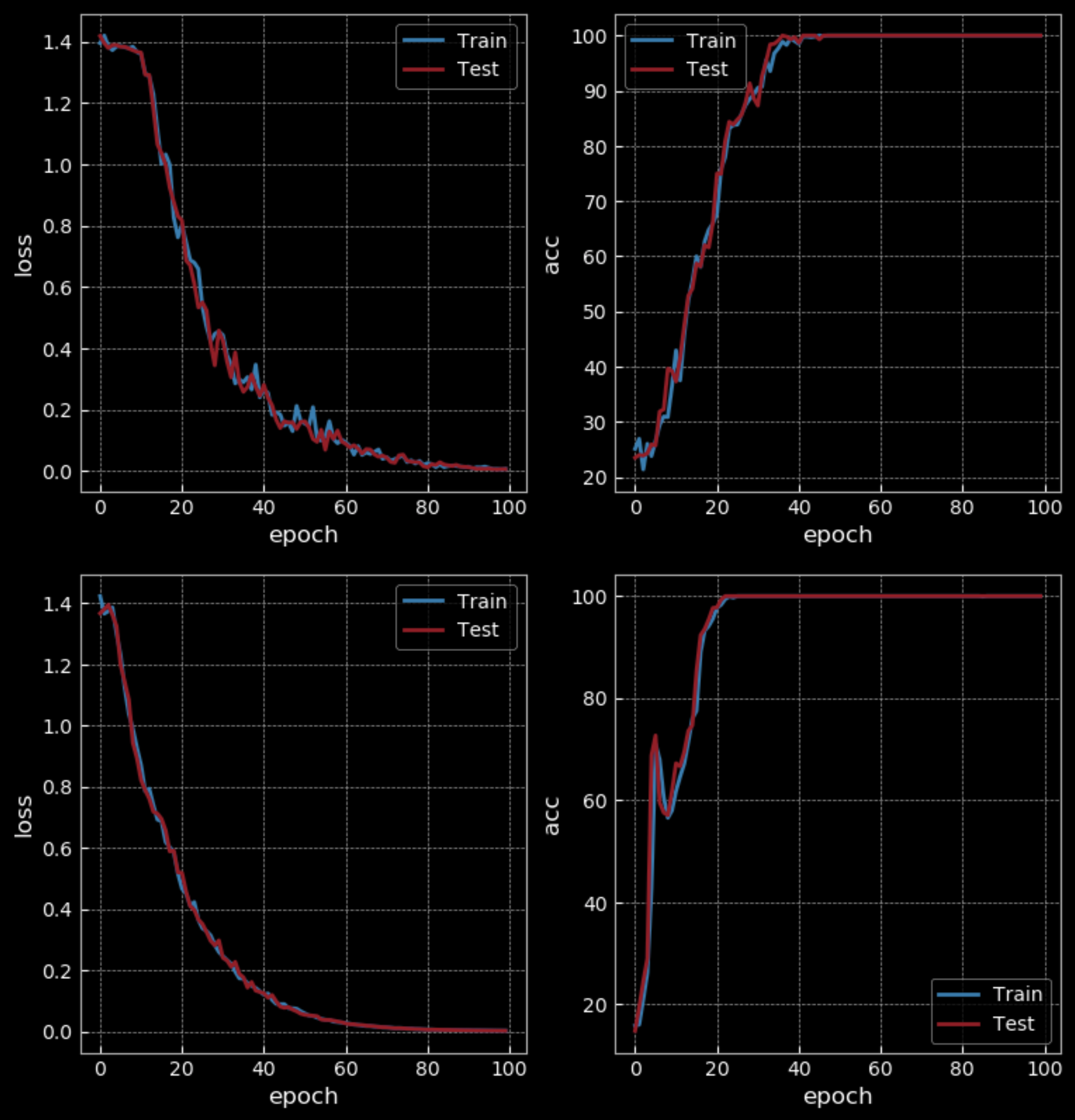
Figura 25: RNN Simple vs LSTM - 100 Epochs

Si aumentamos la dificultad de la parte de entrenamiento (usando secuencias más largas), veremos que la RNN falla, mientras LSTM continúa funcionando.

Figura 26: Visualización de los Valores del Estado Oculto

La visualización anterior está mostrando el valor del estado oculto a lo largo del tiempo en una LSTM. Pasaremos las entradas a través de una tangente hiperbólica, de modo que si la entrada está por debajo de $-2.5$, se asignará un $-1$, y si está por encima de $2.5$, se asignará un $1$. Entonces, en este caso, podemos ver la capa oculta específica que pone su atención en X (quinta fila en la imagen) para luego volverse roja hasta que se observó la otra X. Entonces, la quinta unidad oculta de la celda se activa al observar la X y se queda en silencio después de ver la otra X. Esto es lo que nos permite reconocer la clase de cada secuencia.

Señal de Eco

La señal de eco de n pasos es un ejemplo de tarea sincronizada de muchos-a-muchos. Por ejemplo, la primera secuencia de entrada es "1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 ...", y la primera secuencia objetivo es "0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 ...". En este caso, el resultado es tres pasos después. Por lo tanto, necesitamos una memoria de trabajo de tiempo corto para mantener la información. Mientras que en el modelo de lenguajes, se debe decir algo que aún no se ha dicho.

Antes de enviar toda la secuencia a la red y forzar el objetivo final a ser “algo”, necesitamos cortar la secuencia larga en pequeños trozos. Mientras alimentamos un nuevo fragmento, debemos mantener un estado oculto y enviarlo como entrada al estado interno junto con el siguiente fragmento nuevo. Con LSTMs, se puede mantener la memoria durante mucho tiempo, siempre que tenga suficiente capacidad. En las RNNs, después de alcanzar cierta longitud, se comienza a olvidar lo que sucedió en el pasado.