RNNs, GRUs, LSTMs, Atención, Seq2Seq, y Redes de Memoria

Arquitecturas de Aprendizaje Supervisado

En aprendizaje supervisado, existen diferentes módulos para realizar diferentes funciones. Ser hábil en aprendizaje supervisado implica diseñar arquitecturas para cumplir tareas específicas. Similar a escribir programas con algoritmos para dar instrucciones a una computadora en días pasados, el aprendizaje supervisado reduce una función compleja a un grafo de módulos funcionales (posiblemente dinámico), cuyas funciones son finalizadas por aprendizaje.

Así como lo vimos con las redes convolucionales, la arquitectura de la red es importante.

Redes Recurrentes

En una Red Neuronal Convolucional, el grafo o las interconexiones entre los módulos no pueden tener ciclos. Existe al menos un orden parcial entre los módulos de tal forma que las entradas están disponibles cuando calculamos las salidas.

Como es mostrado en la Figura 1, hay ciclos en las Redes Neuronales Recurrentes.

Figura 1. Red Neuronal Recurrente envuelta

• $x(t)$ : entrada que varía a través del tiempo.
• $\text{Enc}(x(t))$: codificador que genera una representación de la entrada.
• $h(t)$: una representación de la entrada.
• $w$: parámetros entrenables.
• $z(t-1)$: estado oculto previo, el cual es la salida del instante de tiempo previo.
• $z(t)$: estado oculto actual.
• $g$: función que puede ser una complicada red neuronal; una de las entradas es $z(t-1)$ la cual es la salida del instante de tiempo previo.
• $\text{Dec}(z(t))$: decodificador que genera una salida.

Redes Recurrentes: Desenvolviendo el ciclo

Desenvolviendo el ciclo en el tiempo. La entrada es una secuencia $x_1, x_2, \cdots, x_T$.

"
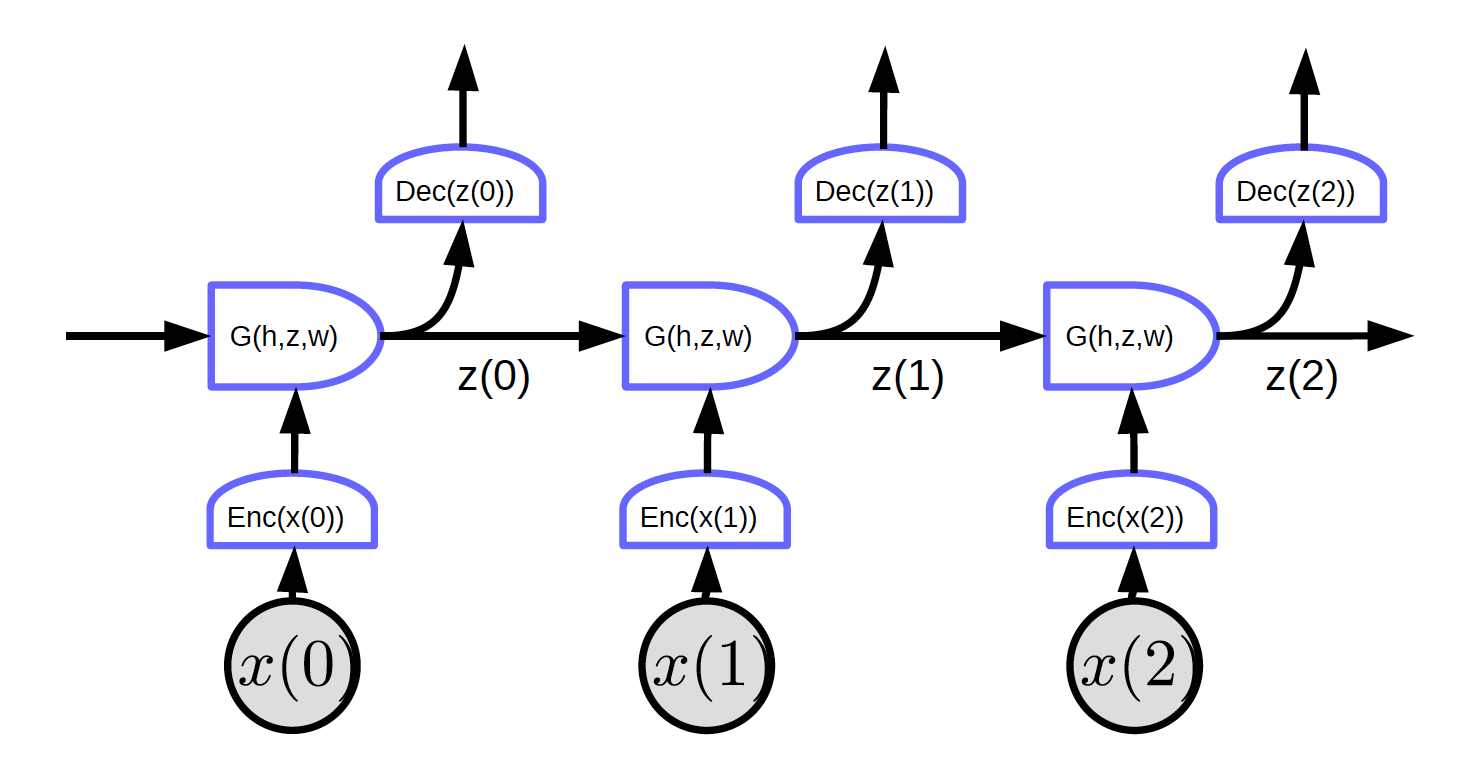
Figura 2. Redes Recurrentes con el ciclo desenvuelto

En la Figura 2, la entrada es $x_1, x_2, x_3$.

En el tiempo t=0, la entrada $x(0)$ es enviada al codificador y este genera la representación $h(x(0)) = \text{Enc}(x(0))$ posteriormente pasa hacia G para generar el estado oculto $z(0) = G(h_0, z’, w)$. En $t = 0$, $z’$ en $G$ puede ser inicializada como $0$ o inicializada aleatoriamente. $z(0)$ es enviado al decodificador para generar una salida y también hacia el siguiente instante de tiempo.

Como no hay ciclos en esta red, podemos implementar propagación hacia atrás.

La Figura 2 muestra una red regular con una característica particular: cada bloque comparte los mismos pesos. Codificadores, decodificadores y funciones G tienen los mismos pesos respectivamente a través de diferentes instantes de tiempo.

BPTT: Propagación hacia atrás a través del tiempo (Brackprop through time). Desafortunadamente, BPTT no funciona muy bien en la forma simplista de una RNN.

Problemas con RNNs:

1. Desvanecimiento de gradientes
   • En una secuencia larga, las gradientes son multiplicadas por la matriz de pesos (transpuesta) en cada instante de tiempo. Si hay valores pequeños en la matriz de pesos, la norma de las gradientes se volverá más pequeña cada vez exponencialmente.
2. Explosión de gradientes
   • Si tenemos una gran matriz de pesos y la no linealidad en la capa recurrente no está saturando, las gradientes explotaran. Los pesos divergirán en el paso de actualización. Podríamos tener que utilizar una tasa de aprendizaje muy pequeña para hacer que el algoritmo de gradiente descendiente funcione.

Una razón para utilizar RNNs es por la ventaja de recordar información en el pasado. Sin embargo, con una simple RNN sin modificaciones, se podría fallar en la memorización de información a largo plazo.

Un ejemplo que tiene el problema de desvanecimiento de gradiente:

La entrada son los caracteres de un programa en C. El sistema dirá cuando este programa es un programa sintácticamente correcto. Un programa sintéticamente correcto debería tener un numero valido de llaves y paréntesis. Así, la red debería recordar cuantos paréntesis y llaves abiertas hay por revisar, y cuando habremos cerrado todas. La red tiene que almacenar dicha información en estados ocultos, como un contador. Sin embargo, debido al desvanecimiento de gradientes, la red fallara en preservar dicha información en un programa muy extenso.

Trucos RNN

• Recorte de gradientes: (evitar la explosión de gradientes). Reducir las gradientes cuando estas se vuelvan muy grandes.
• Inicialización (iniciar en la región aproximada evita el desvanecimiento/explosión de gradientes). Inicializar las matrices de pesos para preservar la norma en algún grado. Por ejemplo, la inicialización ortogonal inicializa la matriz de pesos como una matriz ortogonal aleatoria.

Módulos Multiplicativos

En los módulos multiplicativos en lugar de solo calcular una suma ponderada de entradas, calculamos productos de entradas y luego calculamos la suma ponderada de eso.

Supongamos $x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ and $z \in {R}^{d\times1}$. Aquí U es un tensor.

\(s = \begin{pmatrix} s_1\\ s_2\\ \vdots\\ s_m\\ \end{pmatrix} = Wx = \begin{pmatrix} w_{11} & w_{12} & \cdots &w_{1n}\\ w_{21} & w_{22} & \cdots &w_{2n}\\ \vdots\\ w_{m1} & w_{m2} & \cdots &w_{mn} \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{pmatrix}\) En donde $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

La salida del sistema es una clásica suma ponderada de entradas y pesos. Los pesos por si mismos son también sumas ponderadas de pesos y entradas.

Arquitectura Híper-red: pesos son calculados por otra red.

Atención

$x_1$ y $x_2$ son vectores, $w_1$ y $w_2$ son escalares después de softmax donde $w_1 + w_2 = 1$, y $w_1$ y $w_2$ están entre 0 y 1.

$w_1x_1 + w_2x_2$ es una suma ponderada de $x_1$ y $x_2$ ponderada por coeficientes $w_1$ y $w_2$.

Cambiando el tamaño relativo de $w_1$ y $w_2$, podemos intercambiar la salida de $w_1x_1 + w_2x_2$ a $x_1$ o $x_2$ o a alguna de las combinaciones lineales de $x_1$ y $x_2$.

Las entradas pueden tener múltiples $x$ vectores (más que solo $x_1$ y $x_2$). El sistema escogerá una combinación apropiada, la elección de cual, está determinada por otra variable z. Un mecanismo de atención permite a la red neuronal enfocar su atención en entrada(s) determinadas e ignorar a las otras.

Atención es cada vez más importante en sistemas NLP que utilizan arquitecturas transformadoras u otros tipos de atención.

Los pesos son independientes de los datos porque z es independiente de los datos.

Unidades recurrentes con compuertas (GRU)

Como es mencionado más arriba, las RNNs sufren de desvanecimiento/explosión de gradientes y no pueden recordar estados por mucho. GRU, Cho, 2014, es una aplicación de módulos multiplicativos que intenta resolver estos problemas. Es un ejemplo de red recurrente con memoria (otro es LSTM). La estructura de una unidad GRU es mostrada a continuación:

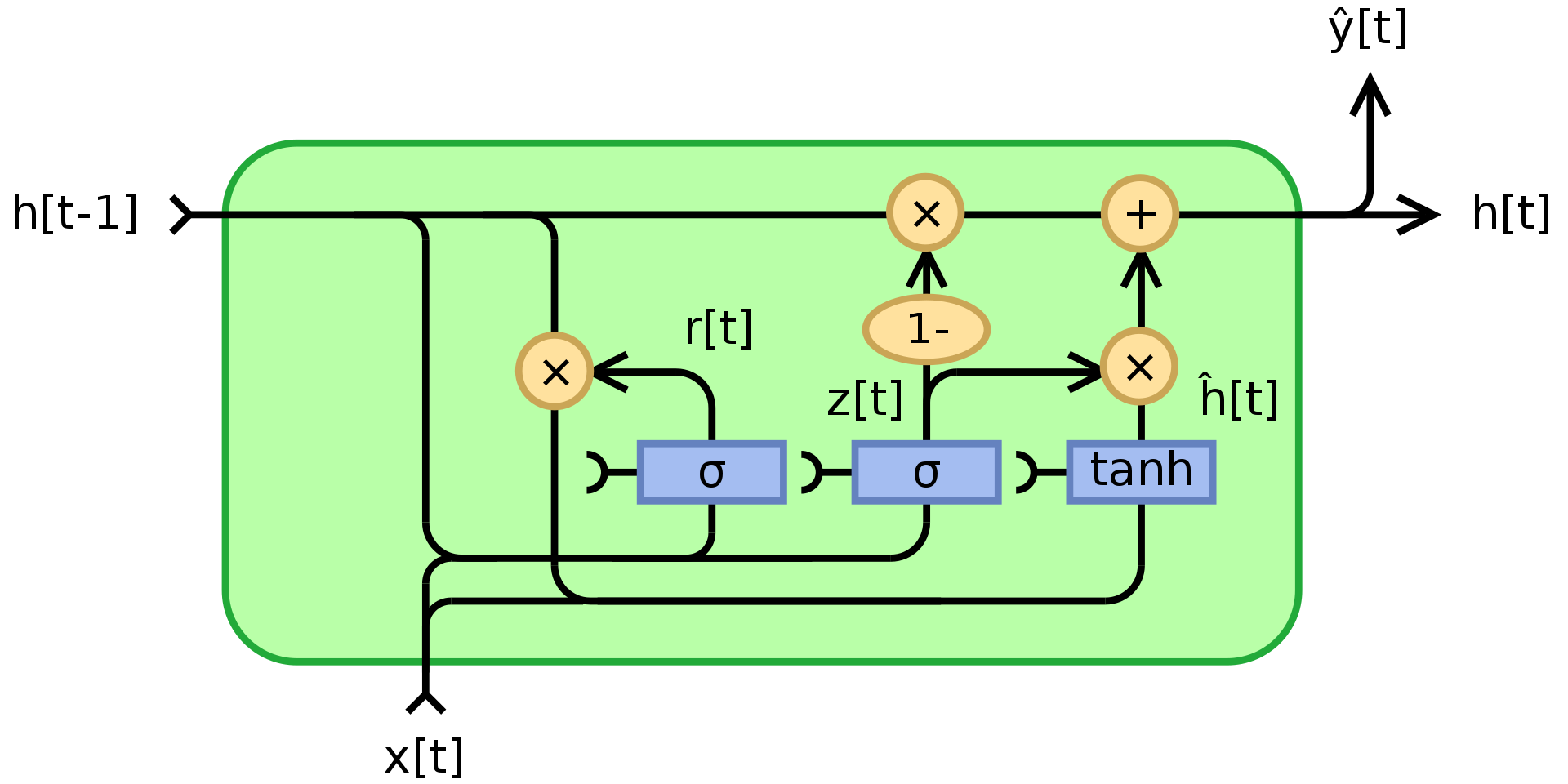
Figura 3. Unidad Recurrente con compuertas

\(\begin{array}{l} z_t = \sigma_g(W_zx_t + U_zh_{t-1} + b_z)\\ r_t = \sigma_g(W_rx_t + U_rh_{t-1} + b_r)\\ h_t = z_t\odot h_{t-1} + (1- z_t)\odot\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h) \end{array}\) En donde $\odot$ denota multiplicación entre elementos (producto Hadamard), $x_t$ es el vector de entrada, $h_t$ es el vector de salida, $z_t$ es el vector de compuerta de actualización, $r_t$ es el vector de compuerta de reinicio, $\phi_h$es una tan hiperbólica tanh, y $W$,$U$,$b$ son parámetros aprendibles.

Para ser específicos, $z_t$ es un vector compuerta que determina cuanto de la información del pasado debería ser enviada hacia el futuro. Aplica una función sigmoide a la suma de dos capas lineales y un sesgo sobre la entrada $x_t$ y el estado previo $h_{t-1}$. $z_t$ contiene coeficientes entre 0 y 1 como resultado de aplicar sigmoide. El estado final de salida $h_t$es una combinación convexa de $h_{t-1}$ y $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ vía $z_t$. Si el coeficiente es 1, la unidad actual de salida es simplemente una copia del estado previo e ignora la entrada (lo cual es el comportamiento por defecto). Si es menos que uno, se tomara en cuenta alguna nueva información proveniente de la entrada.

La compuerta de reinicio $r_t$es utilizada para decidir cuanto olvidar de la información del pasado. En el nuevo contenido de la memoria $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$, si el coeficiente en $r_t$ es 0, entonces no se almacena nada de la información del pasado. Si al mismo tiempo $z_t$ es 0, entonces el sistema es completamente reiniciado ya que $h_t$ solo vería a la entrada.

LSTM (Gran Memoria a corto plazo)

GRU es en realidad una versión simplificada de LSTM la cual surgió mucho antes, Hochreiter, Schmidhuber, 1997. Agrupando celdas de memoria para preservar información pasada, LSTMs también tienen como propósito resolver los problemas de pérdida de memoria a largo plazo en las RNNs. La estructura de las LSTMs se muestra a continuación:

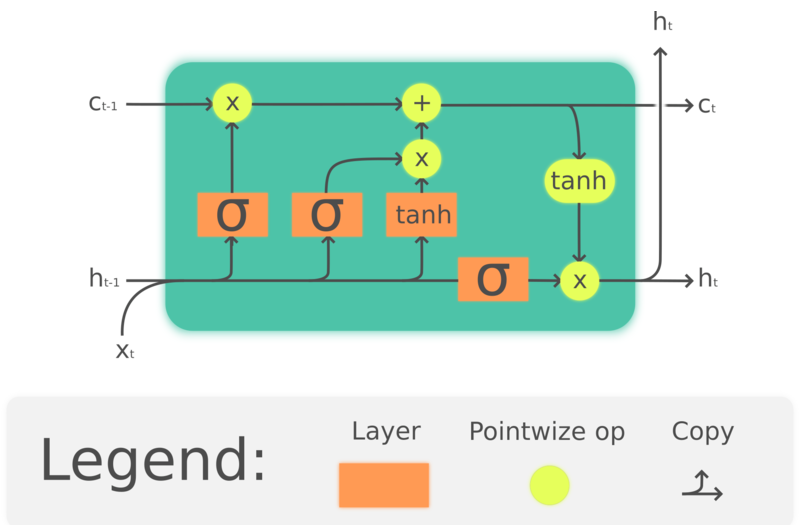
Figura 4. LSTM

\(\begin{array}{l} f_t = \sigma_g(W_fx_t + U_fh_{t-1} + b_f)\\ i_t = \sigma_g(W_ix_t + U_ih_{t-1} + b_i)\\ o_t = \sigma_o(W_ox_t + U_oh_{t-1} + b_o)\\ c_t = f_t\odot c_{t-1} + i_t\odot \tanh(W_cx_t + U_ch_{t-1} + b_c)\\ h_t = o_t \odot\tanh(c_t) \end{array}\) En donde $\odot$ denota multiplicación entre elementos, $x_t\in\mathbb{R}^a$ es un vector de entrada hacia la unidad LSTM, $f_t\in\mathbb{R}^h$ es el vector de activación de la compuerta de olvido, $i_t\in\mathbb{R}^h$ es el vector de activación de la compuerta de entrada/actualización, $o_t\in\mathbb{R}^h$ es el vector de activación de la compuerta de salida, $h_t\in\mathbb{R}^h$ es el vector de estados ocultos (también conocido como salida),$c_t\in\mathbb{R}^h$ es el vector de estado de la celda.

Una unidad LSTM utiliza un estado de celda $c_t$ para transportar información a través de la unidad. Regula cuanta información es preservada o removida del estado de la celda a través de estructuras llamadas compuertas. La compuerta de olvido $f_t$ decide cuanta información proveniente del estado de la celda previa $c{t-1}$ queremos preservar, observando la entrada actual y el estado oculto previo, produce un numero entre 0 y 1 como el coeficiente de $c{t-1}$. $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ calcula un nuevo candidato para actualizar el estado de la celda, y al igual que la compuerta de olvido, la compuerta de entrada $i_t$ decide cuanto de la actualización será aplicada. Finalmente, la salida $h_t$ estará basada en el estado de celda $c_t$, pero será puesta a través de una $\tanh$ que luego será filtrada por la compuerta de salida $o_t$.

Aunque LSTMs son ampliamente usadas en NLP, su popularidad está disminuyendo. Por ejemplo, el reconocimiento del habla se está moviendo hacia la utilización de redes CNN temporales, y NLP está moviéndose hacia la utilización de transformadores.

Modelo Secuencia a Secuencia

El enfoque propuesto por Sutskever NIPS 2014 es el primer sistema de máquina neuronal de traducción en tener un rendimiento comparable a enfoques clásicos. Utiliza una arquitectura codificador-decodificador donde ambos el codificador y el decodificador son LSTMs multicapa.

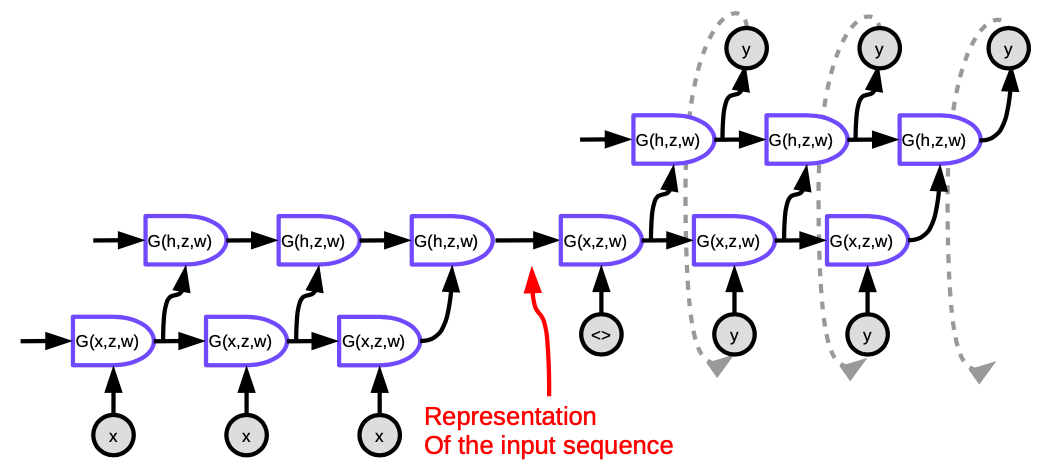
Figura 5. Seq2Seq

Cada celda en la figura es una LSTM. Para el codificador (la parte en la izquierda), el número de pasos de tiempo es igual a la longitud de la secuencia a ser traducida. En cada paso, hay una pila de LSTMs (cuatro capas en la publicación original) donde el estado oculto de la LSTM previa es alimentado hacia el siguiente. La última capa del último paso de tiempo entrega un vector que representa el significado de la oración completa, la cual es luego enviada hacia otra LSTM multicapa (el decodificador), que produce palabras en el lenguaje objetivo. En el decodificador, el texto es generado en una forma secuencial. Cada paso produce una palabra, la cual será una entrada para el siguiente paso de tiempo.

Esta arquitectura no es satisfactoria de dos maneras: Primero, el significado completo de la oración tiene que ser comprimido hacia el estado oculto entre el codificador y el decodificador. Segundo, las LSTMs realmente no preservan información por más que cerca de 20 palabras. La solución para estos problemas es llamada Bi-LSTM, la cual ejecuta dos LSTMs en direcciones opuestas. En una Bi-LSTM el significado es codificado en dos vectores, uno generado por ejecutar la LSTM de izquierda a derecha, y otro de derecha a izquierda. Esto permite duplicar la longitud de la oración sin perder mucha información.

Seq2seq con Atención

El éxito del enfoque antes mencionado fue de corta vida. Otra publicación por Bahdanau, Cho, Bengio sugería que en lugar de tener una gigantesca red que comprima el significado de la oración entera en un vector, tendría más sentido si en cada paso de tiempo solamente enfocáramos la atención en las ubicaciones relevantes en el lenguaje original con significado equivalente, i.e. el mecanismo de atención.

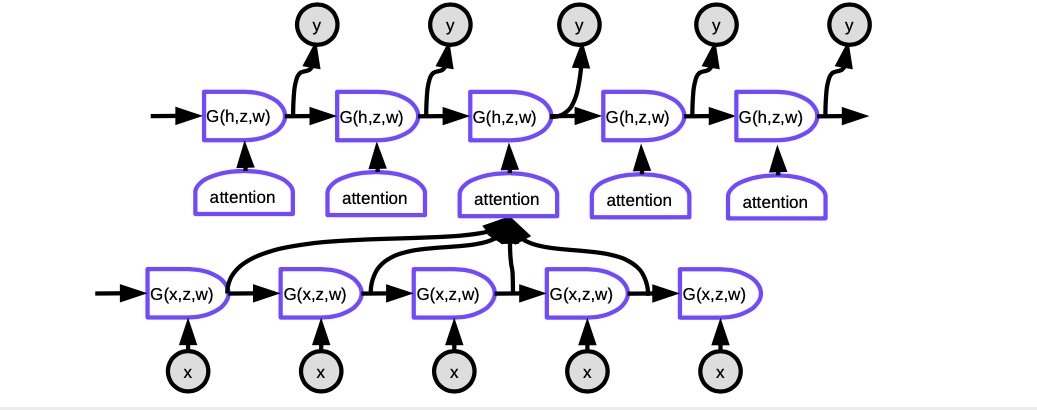
Figura 6. Seq2Seq con Atención

En atención, para producir la palabra actual en cada paso de tiempo, necesitamos decidir en cuales representaciones ocultas de palabras en la oración de entrada enfocarnos. Esencialmente, una red aprenderá a evaluar que tan bien cada entrada codificada coincide con la salida actual del decodificador. Estos punteos son normalizados por una función softmax, luego los coeficientes son utilizados para calcular una suma ponderada de los estados ocultos en el decodificador en diferentes pasos de tiempo. Ajustando los pesos, el sistema puede ajustar el área de entrada para enfocarse. La magia de este mecanismo es que la red utilizada para calcular los coeficientes puede ser entrenada a través de la propagación hacia atrás. ¡No hay necesidad de construirlas a mano!

Los mecanismos de atención transformaron completamente la traducción con máquinas neuronales. Tiempo después, Google publicó Atención Es Todo Lo Que Tú Necesitas, ellos colocaron un transformador hacia adelante, donde cada capa y grupo de neuronas está implementando atención.

Red de Memoria

Las redes de memoria tienen sus raíces del trabajo en Facebook que fue iniciado por Antoine Bordes en 2014 y Sainbayar Sukhbaatar en 2015.

La idea de una red de memoria es que existen dos partes importantes en el cerebro: una es la corteza, que es donde se tiene la memoria a largo plazo. Existe un pedazo separado de neuronas llamado el hipocampo que envía conexiones a casi todas partes en la corteza. El hipocampo está pensado para ser utilizado por la memoria a corto plazo, recordando cosas por un relativo corto periodo de tiempo. La teoría predominante es que cuando se duerme, hay un montón de información transferida desde el hipocampo hacia la corteza para ser solidificada en la memoria a largo plazo ya que el hipocampo tiene capacidad limitada.

Para una red de memoria, existe una entrada a la red, $x$ (piensa en esto como una dirección de memoria), y compara esto $x$ con vectores $k_1, k_2, k_3, \cdots$ (“claves”) a través del producto punto. Coloca todo esto a través de una función softmax, lo que obtienes es un arreglo de números que suman uno. Existe otro conjunto de otros vectores $v_1, v_2, v_3, \cdots$ (“valores”). Multiplica estos vectores por los escalares obtenidos de la función softmax y la suma de estos vectores (note el parecido al mecanismo de atención) le dará el resultado.

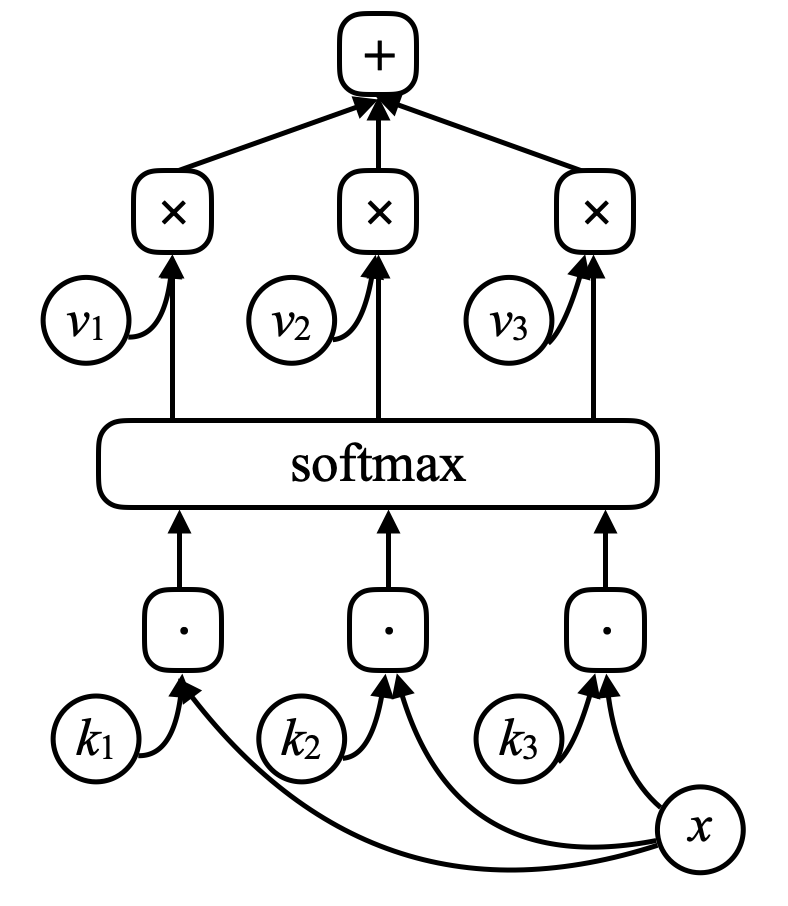
Figura 7. Red de Memoria

Si una de estas claves (e.g. $k_i$) coincide exactamente con $x$, entonces el coeficiente asociado con esta clave será muy cercano a uno. Entonces la salida del sistema será esencialmente $v_i$.

Esta es una memoria direccionable asociativa. La memoria asociativa es aquella que, si tu entrada coincide con una clave, obtienes ese valor. Y estos es justamente a versión suave diferenciable de él, el cual permite la propagación hacia atrás y cambiar los vectores a través del gradiente descendiente.

Lo que los autores hicieron fue contarle una historia a un sistema entregándole una secuencia de oraciones. Estas oraciones son codificadas en vectores ejecutándolas a través de una red neuronal que no ha sido pre-entrenada. Las oraciones son regresadas a la memoria de este tipo. Cuando realizas una pregunta al sistema, codificas la pregunta y la colocas como entrada de una red neuronal, la red neuronal produce un $x$ en la memoria, y la memoria retorna un valor.

Este valor, junto con el estado previo de la red, es utilizado para re-acceder a la memoria. Y puedes entrenar esta red completa para producir una respuesta a tu pregunta. Después de un entrenamiento extenso, este modelo realmente aprende a almacenar historias y responder preguntas.

En una red de memoria, existe una red neuronal que toma una entrada y produce una dirección para la memoria, regresa el valor hacia la red, se mantiene ejecutando, y eventualmente produce una salida. Esto es muy parecido a una computadora ya que hay un CPU y una memoria externa para leer y escribir.

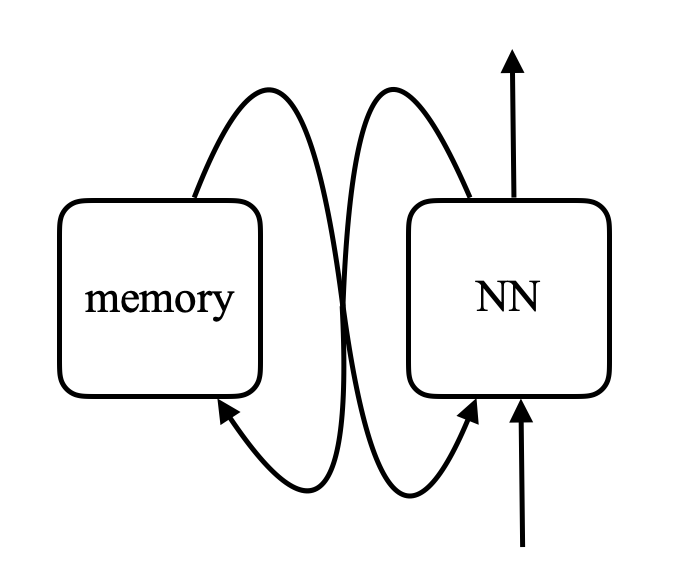
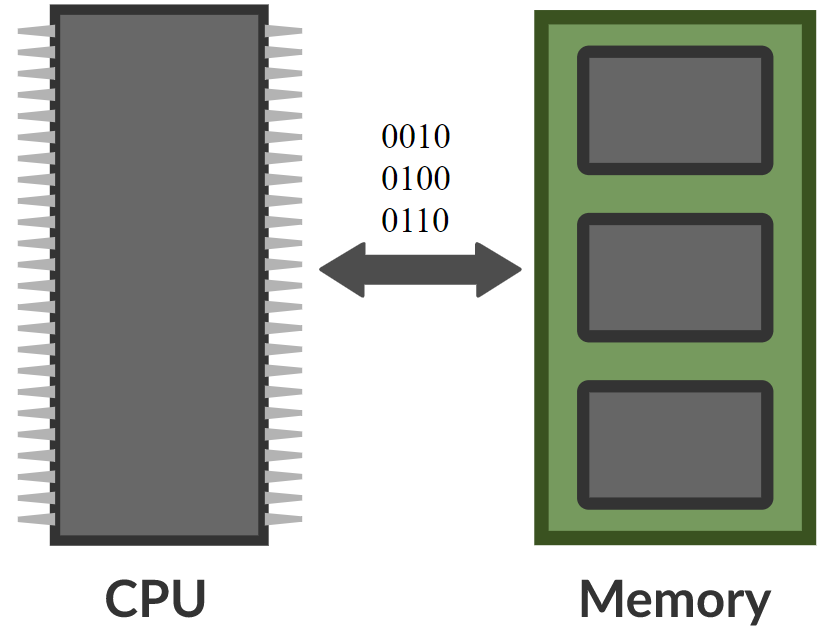
Figura 8. Comparación entre una red de memoria y una computadora (Foto por Khan Academy)

Existen personas que imaginan que se puede realmente construir computadoras diferenciables fuera de esto. Un ejemplo es la Máquina Neuronal de Turing de DeepMind, que fue hecha pública tres días después de que la publicación de Facebook fuera publicada en arXiv.

La idea es comparar entradas con claves, generar coeficientes, y producir valores – lo cual es básicamente lo que un transformador es. Un transformador es básicamente una red neuronal en la cual cada grupo de neuronas es una de estas redes.