Entendiendo las convoluciones y el motor de diferenciación automática

Entendiendo la convolución 1D

En esta parte trataremos convoluciones, ya que queremos explorar la raleza, estacionalidad y composicionalidad de los datos.

En vez de usar la matriz $A$ tratada en la semana previa, cambiaremos el ancho de la matriz por el tamaño del núcleo $k$. Así, cada fila de la matriz es un núcleo. Podemos usar los núcleos apilándolos y desplazándolos (ver Fig 1). Así, podemos tener $m$ capas de alto $n-k+1$.

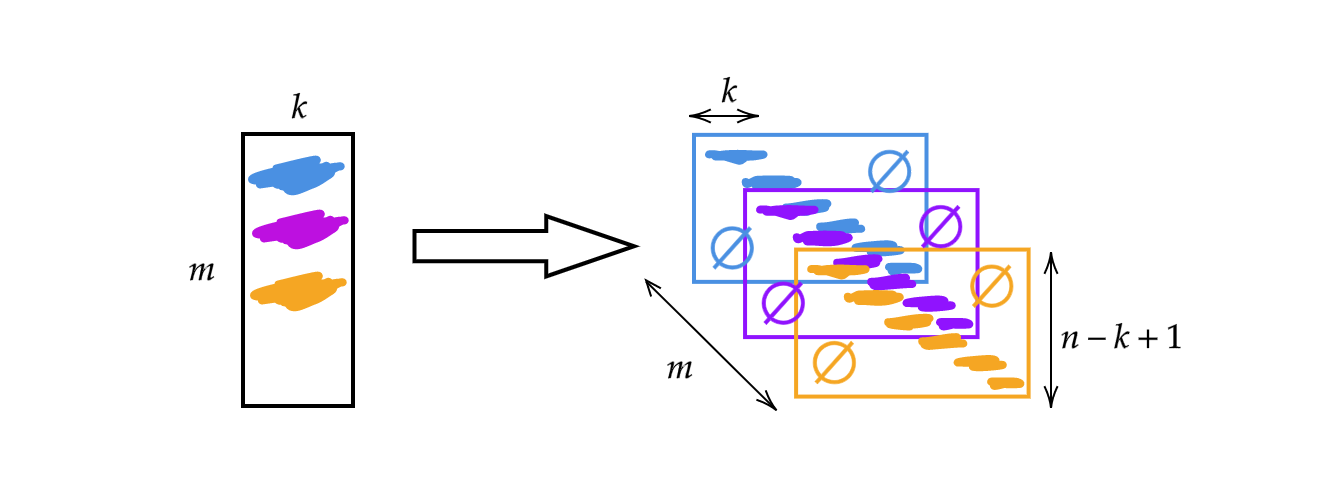
Fig 1: Ilustración de Convolución 1D

La salida is $m$ (grosor) vectores de tamaño $n-k+1$.

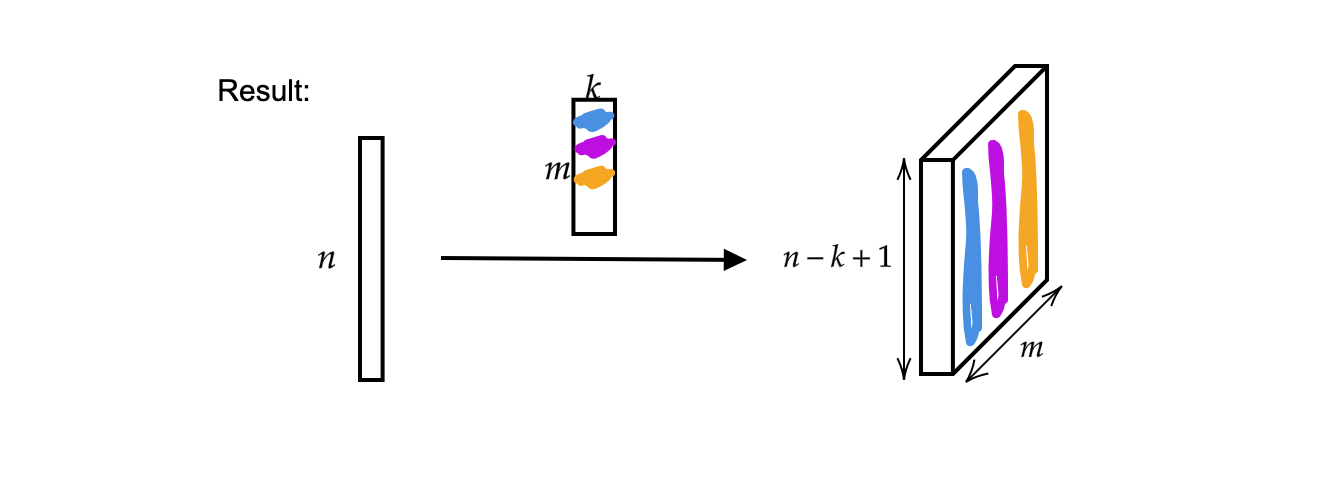
Fig 2: Resultado de Convolución 1D

Además, un único vector de entrada puede ser visto como una señal mono-canal.

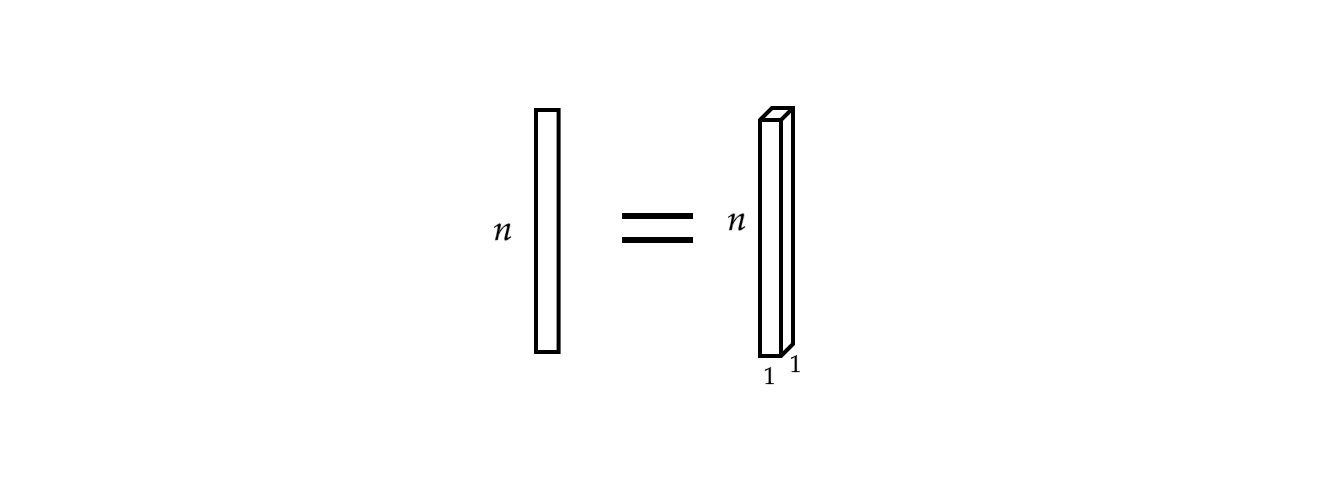
Fig 3: Señal mono-canal

Ahora, la entrada $x$ es un mapeo

donde $\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb{N}^1$ (ya que es una señal $1$ dimensional / tiene un dominio $1$ dimensional) y en este caso el número de canal $c$ es $1$. Cuando $c = 2$ se convierte en una señal estereofónica.

Para la convolución 1D, podemos simplemente computar el producto escalar, núcleo por núcleo (ver Fig 4).

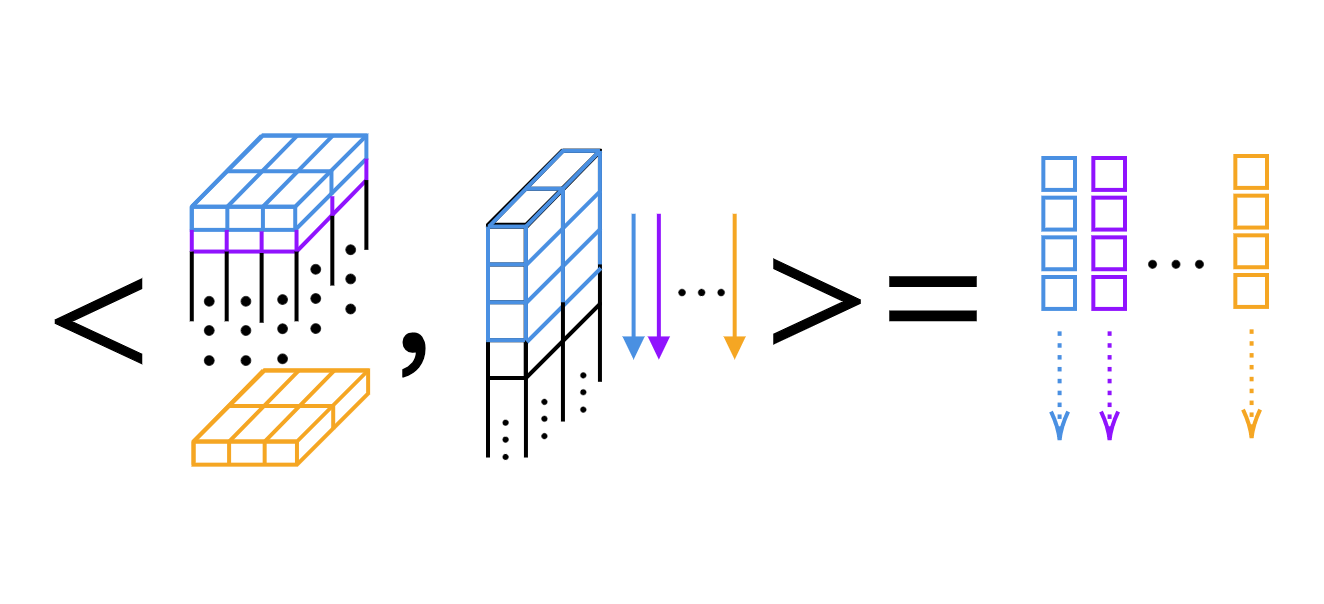
Fig 4: Producto escalar de una convolución 1D capa por capa

Dimensiones de núcleos y ancho de salida en Pytorch

Consejo: podemos usar signo de pregunta en IPython para acceder a la documentación de funciones. Por ejemplo,

Init signature:
nn.Conv1d(
	in_channels,           # nro de canales en la imagen de entrada
	out_channels,          # nro de canales que genera la convolución
	kernel_size,           # tamaño del núcleo convolucionante
	stride=1,              # paso de la convolución
	padding=0,             # relleno de ceros a ambos lados de la entrada
	dilation=1,            # espaciado entre los elementos del núcleo
	groups=1,              # nro de conecciones bloqueadas entre E/S
	bias=True,             # Si `True`, agrega un sesgo aprendible a la salida
	padding_mode='zeros',  # aceptar valor `zeros` y `circular`
)

Convolución 1D convolution

Tenemos una convolución $1$ dimensional que va desde una señal de $2$ canales (señal estereofónica) a $16$ canales ($16 núcleos) con tamaño de núcleo $3$ y paso de $1$. Entonces tendremos $16$ canales de grosor $2$ y largo $3$. Asumamos que la señal de entrada tiene un tamaño de lote de $1$ (una señal), $2$ canales y $64$ muestras. La capa de salida resultante tiene una señal, $16$ canales y el largo de la señal es de $62$ ($=64-3+1). También, si imprimimos el tamaño del sesgo, encontraremos que su tamaño es de $16$, ya que tenemos un sesgo para cada peso.

conv = nn.Conv1d(2, 16, 3)  # 2 canales (señal estére), 16 núcleos de tamaño 3
conv.weight.size()          # salida: torch.Size([16, 2, 3])
conv.bias.size()            # salida: torch.Size([16])

x = torch.rand(1, 2, 64)    # lote de tamaño 1, 2 canales, 64 muestras
conv(x).size()              # sailda: torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5)  # 2 canales, 16 núcleos de tamaño 5
conv(x).size()              # salida: torch.Size([1, 16, 60])

Convolución 2D

Primero definimos los datos de entrada como una muestra, $20$ canales (imágen hiper-espectral) con alto $64$ y ancho $128$. La convolución 2D tiene $20$ canales desde la entrada y $16$ núcleos de tamaño $3$ \times $5. Luego de la convolución, los datos de salida tienen una muestra, $16$ canales con alto $62$ $(=64-3+1) y ancho $124$ $(=128-5+1$).

x = torch.rand(1, 20, 64, 128)    # 1 salida, 20 canales, alto 64, y ancho 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 canales, 16 núcleos, tamaño núcleo 3 x 5
conv.weight.size()                # salida: torch.Size([16, 20, 3, 5])
conv(x).size()                    # salida: torch.Size([1, 16, 62, 124])

Si queremos obtener la mismas dimensiones, podemos usar relleno. Continuando el código de arriba, podemos agregar nuevos parámetros a la función de convolución stride=1 y padding=(1, 2), que significa $1$ en la dirección de $y$ ($1$ arriba y $1$ abajo) y $2$ en la dirección de $x$. Así, la señal de salida es del mismo tamaño que la señal de entrada. El número de dimensiones que se requiere para almacenar la colección de núcleos cuando se realiza convolución 2D es de $4$.

# 20 canales, 16 núcleos de tamaño 3 x 5, paso es 1, relleno de 1 y 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size()  # salida: torch.Size([1, 16, 64, 128])

Cómo funcionan los gradientes automáticos?

En esta sección vamos a pedirle a torch que corrobore todos los cálculos realizados con los tensores de manera que podamos realizar el cálculo de las derivadas parciales.

• Crear un tensor $2\times2$ $\boldsymbol{x}$ con capacidad de acumular gradiente;
• Restar $2$ de todos los elementos $\boldsymbol{x}$ y obtener $\boldsymbol{y}$; (Si imprimimos y.grad_fn, tendremos <SubBackward0 object at 0x12904b290>, que significa que y es generado por el módule de resta $\boldsymbol{x}-2$. También podemos usar y.grad_fn.next_functions[0][0].variable para derivar el tensor original.)
• Hacemos más operaciones: $\boldsymbol{z} = 3\boldsymbol{y}^2$;
• Calcular la media de $\boldsymbol{z}$.

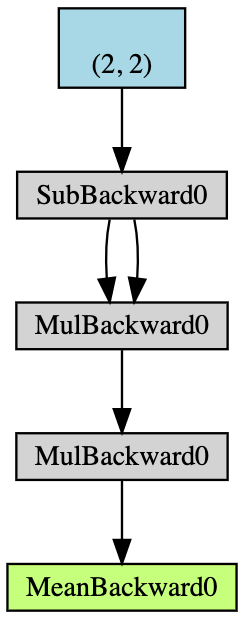
Fig 5: Flujo del auto-gradiente del ejemplo

La retro propagación se usa para el cálculo de los gradientes. En este ejemplo, el proceso de retro propagación puede ser visto como el cálculo del gradiente $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$. Luego de calcular $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$ a mano como validación, encontramos que la ejecución de a.backward() nos da el mismo valor de x.grad que el cálculo automático.

Este es el proceso de hacer a mano la retro propagación:

Siempre que se usen derivadas parciales en PyTorch, obtenemos las mismas dimensiones que los datos originales. Sin embargo, el Jacobiano debe trasponerse.

De lo básico a lo más alocado

Ahora tenemos un vector $x$ $1\times3$, asignamos $y$ al doble de $x$ y continuamos duplicando $y$ mientras que su norma sea menor que $1000$. Debido a la aleatoridad que tenemos para $x$, no podemos saber de antemano la cantidad de iteraciones hasta que termine el procedimiento.

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

Sin embargo, podemos inferirlo conociendo los gradientes que tenemos.

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

Al igual que para la inferencia, podemos usar requires_grad=True para denotar que queremos restrear la acumulación de gradiente como se muestra abajo. Si omitimos requires_grad=True ya sea en la declaración de $x$ o $w$ y llamamos a backward() con $z$, ocurrirá un error de ejecución debido a que no tenemos acumulación de gradiente para $x$ o $w$.

# Permitir acumulación de gradiente tanto para x como w
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

Y con with torch.no_grad() podemos omitir la acumulación de gradiente.

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# Todos los tensores no tendrán acumulación de gradiente
with torch.no_grad():
    z = w @ x

try:
    z.backward()  # PyTorch lanzará error aquí, ya que z acumula gradiente.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

Más cosas – gradientes personalizados

Además de las operaciones numéricas básicas, podemos definir nuestros propios módulos / funciones, que pueden insertarse en el grafo neuronal. La Jupyter Notebook relacionada puede encontrase aquí.

Para hacerlo, debemos heredar torch.autograd.Function y sobre escribir las funciones forward() y backward(). Por ejemplo, si queremos entrenar redes, necesitamos hacer la pasada hacia adelante y conocer las derivadas parciales de las entradas respecto de las salidas, de manera que podamos usar este módulo en cualquier punto del código. Luego, mediante la utilización de retro propagación (regla de la cadena), podemos insertar el módulo en cualquier lugar de la cadena de operaciones, en tanto y en cuanto conozcamos las derivadas parciales de la entrada con respecto a las salidas.

En este caso, hay tres ejemplos de módulos personalizados en el notebook, los módulos add, split y max. Por ejemplo, el módulo personalizado de suma:

# módulo sumador personalizado
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx es un contexto donde podemos guardar
        # cálculos para atrás.
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # se necesita retornar gradientes en el orden
        # de la entradas del método forward (excluir ctx)
        return grad_x1, grad_x2

Si tenemos la suma de dos cosas y obtenemos una salida, necesitamos sobre escribir la función forward como se muestra. Y para realizar la retro propagación, necesitamos sobre escribir la funcion backward de manera de retornar los gradientes.

Para los casos de split and max, ver el código de como se sobre escriben las funciones en el notebook. Para el caso de Split, cuando hacemos los gradientes deberiamos sumarlos. Para argmax, que selecciona el indice del mayor elemento, entonces el índice del mayor debería ser $1$ mientras que el resto $0$. Recordar que de acuerdo para diferentes módulos personalizados, debemos sobre escribir la pasada hacia adelante y la pasada hacia atrás siempre.