Técnicas de Optimización II

Métodos Adaptativos

Actualmente SGD con momentum es el estado del arte en métodos de optimización para muchos problemas de ML. Pero hay otros métodos, llamados genéricamente Métodos Adaptativos, innovados recientemente que son particularmente útiles para problemas con condiciones pobres (si SGD no sirve).

En la formulación de SGD, cada peso en la red es actualizado utilizando una ecuación con la misma taza de aprendizaje (global $\gamma$). En cambio, para los métodos adaptativos, adaptamos una taza de aprendizaje para cada peso individualmente. Para este propósito, es usada la informacion obtenida de los gradientes de cada peso.

Las redes mas utilizadas en la práctica tienen diferente estructura en diferentes partes. Por ejemplo, las primeras partes de una red CNN pueden ser capas convolucionales muy superficiales sobre imágenes grandes y luego en la red podemos tener convoluciones con una gran cantidad de canales sobre imágenes pequeñas. Ambas operaciones son muy diferentes, entonces una taza de aprendizaje que anda bien para el principio de la red puede no andar bien para las últimas secciones de la red. Esto significa que tasas de aprendizaje adaptativas por capa pueden llegar a ser útiles.

Los pesos en la parte final de la red (4096 en figura 1 abajo) directamente impone la salida y tiene un fuerte peso sobre ella. Por eso, necesitamos tasas de aprendizaje menores para estos casos. En contraste, los primeros pesos tendrán efectos individuales menores en la salida, especialmente cuando son inicializados aleatoriamente.

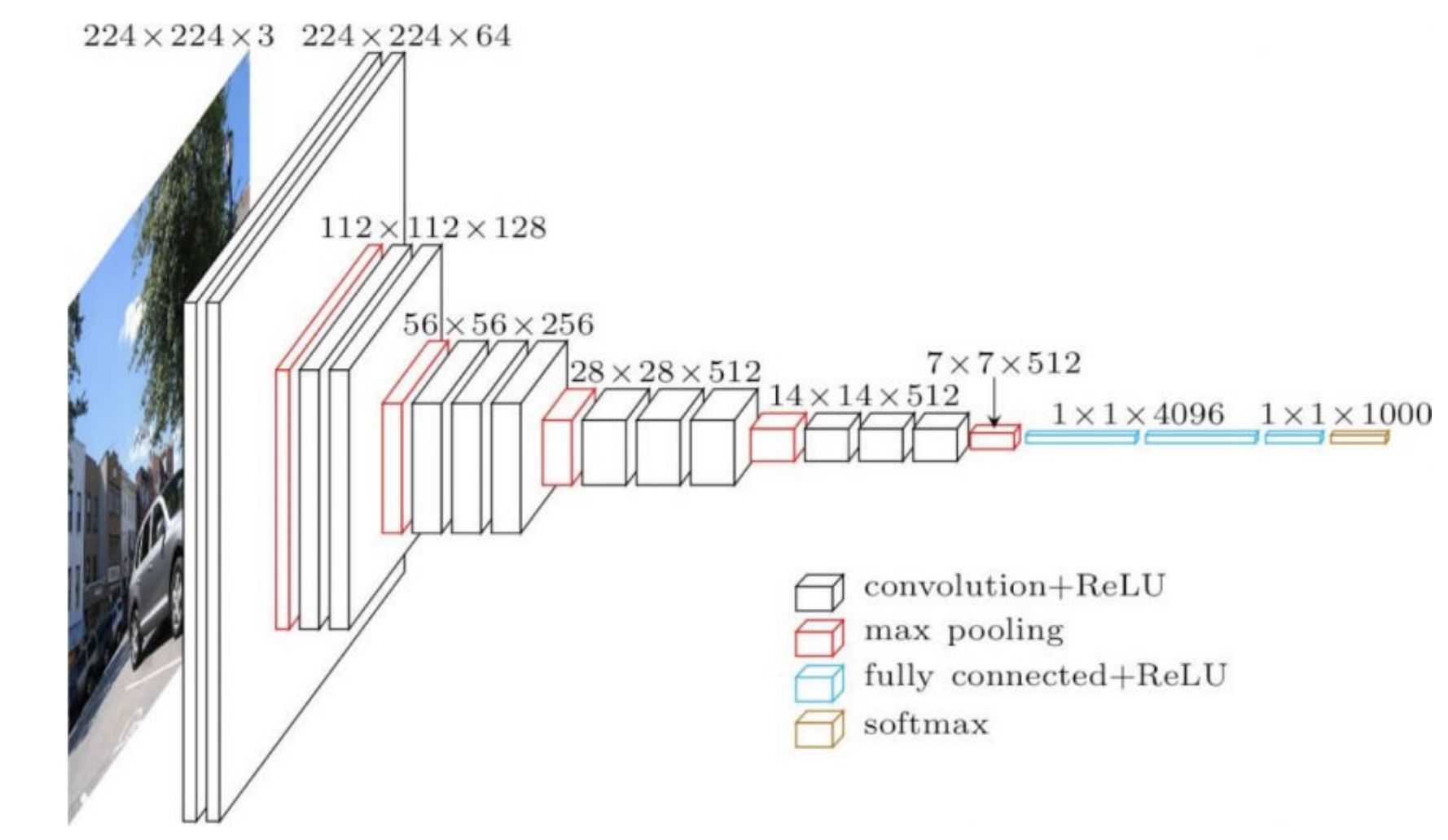
Figure 1: VGG16

RMSprop

La idea central de Root Mean Square Propagation es normalizar el gradiente con su raíz cuadrada del valor medio de los cuadrados.

En la ecuación de abajo, elevando al cuadrado el gradiente denota que cada elemento del vector es elevado al cuadrado individualmente.

\(\begin{aligned} v_{t+1} &= {\alpha}v_t + (1 - \alpha) \nabla f_i(w_t)^2 \\ w_{t+1} &= w_t - \gamma \frac {\nabla f_i(w_t)}{ \sqrt{v_{t+1}} + \epsilon} \end{aligned}\)

donde $\gamma$ es la taza global de aprendizaje, $\epsilon$ es un valor infinitesimal $\epsilon$ (on the order of $10^{-7}$ or $10^{-8}$) (para evitar errores de división por cero), y $v_{t+1}$ es la estimada del 2do. momento.

Actualizamos $v$ para estimar esta cantidad ruidosa via un exponential moving average (que es la forma estándar de mantener el promedio de una cantidad que puede cambiar en el tiempo). Necesitamos poner mayores pesos en los valores recientes ya que proporcionan mayor información. Una manera de hacerlo es bajando de peso valores viejos exponencialmente. Los valores en el cálculo de $v$ son bajados de peso en cada paso por una constante $\alpha$, que varía entre 0 and 1. Esto disminuye los valores viejos hasta que dejan de ser una parte importante del promedio móvil exponencial.

El método original mantiene promedio móvil exponencial de un momento de segundo orden no-central. El momento de segundo orden es usado para normalizar todos los elementos del gradiente, lo que significa que cada elemento del gradiente es dividido por la raíz cuadrada de la estimada del momento de segundo orden. Si el valor esperado del grandiente es pequeño, este proceso es similar a dividir el gradiente por la desviación estándar.

Utilizando un $\epsilon$ pequeño en el denominador no diverge porque cuando $v$ es muy pequeño, el momento es muy pequeño también.

ADAM

ADAM, or Estimación Adaptativa del Momento, que es RMSprop más momento, es un método comunmente más usado. La actualización del momento se convierte en un promedio móvil exponencial sin querer cambiar la taza de aprendizaje cuando tratamos con $\beta$ . Justo como en RMSprop, aquí tomamos el promedio móvil exponencial del gradiente cuadrado.

donde $m_{t+1}$ es el promedio móvil exponencial del momento.

Aquí no se muestra la correción de sesgo que es usada durante las primeras iteraciones para mantener sin sesgo el promedio móvil.

Lado práctico

Cuando se entrenan redes neuronales, a menudo al principio del proceso de entrenamiento SGD va en la dirección equivocada, mientras que RMSprop enfila hacia la dirección correcta. Sin embargo, RMSprop, al igual que SGD, es sensible al ruido, por lo que generalmente rebota significativamente alrededor del punto óptimo cuando está cerca de un mínimo local.

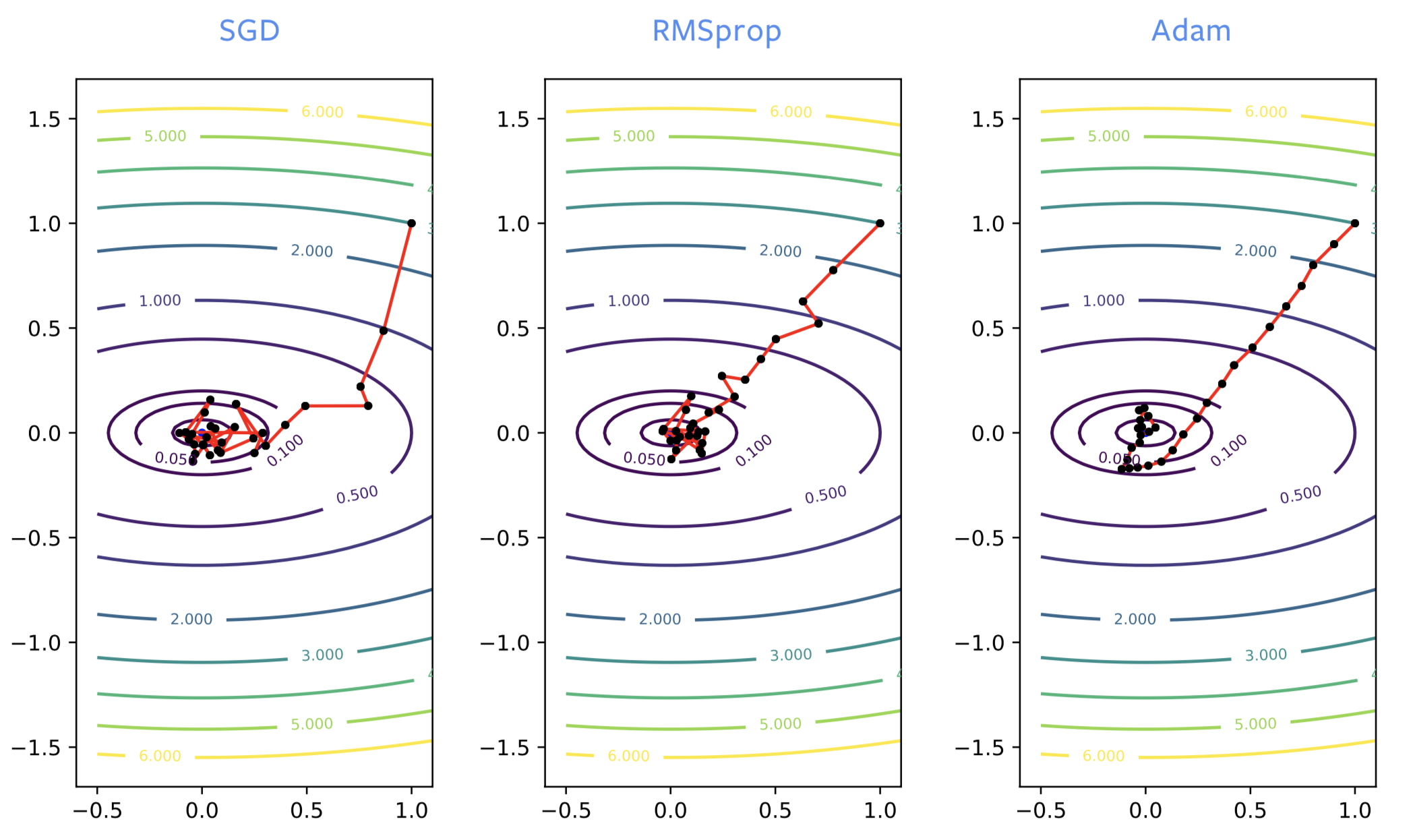
Figura 2: SGD vs RMSprop vs ADAM

ADAM es necesario para el entrenamiento de algunas de las redes que usan modelos del lenguage. Para la optimización de redes neuronales, se prefiere generalmente SGD con momento o ADAM. Sin embargo, la teoría de ADAM en los papers no es bien entendida y tiene varias desventajas:

• Se puede demostrar haciendo pruebas muy simples que el método no converge.
• Se sabe que produce errores de generalización. Si la red neuronal es entrenada de manera que la pérdida es cero en el conjunto de datos de entrenamiento, entonces la pérdida en puntos de datos desconocidos no será cero. Es bastante común, particulamente en problemas con imágenes, que se obtengan peores errores de generalización que cuando se usa SGD.
• Con ADAM se necesitan 3 memorias intermedias, mientras que con SGD se necesitan sólo 2. Esto importa solamente si entrenamos modelos cuyo tamaño son del orden de varios gigabytes ya que podrían no entrar en la memoria.
• Se deben sintonizar dos parámetros de momento en lugar de 1.

Capas de normalización

Las capas de normalización más que mejorar los algoritmos de optimización, mejoran la estructura de la red en sí misma. Se conforman por capaz adicionales entre las capas existentes. El objetivo es mejorar las prestaciones de la optimización y la generalización.

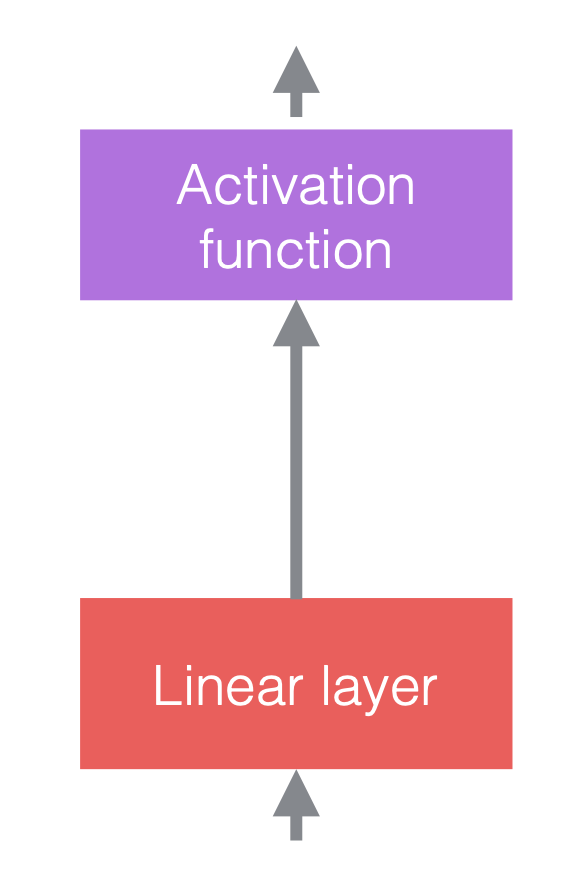
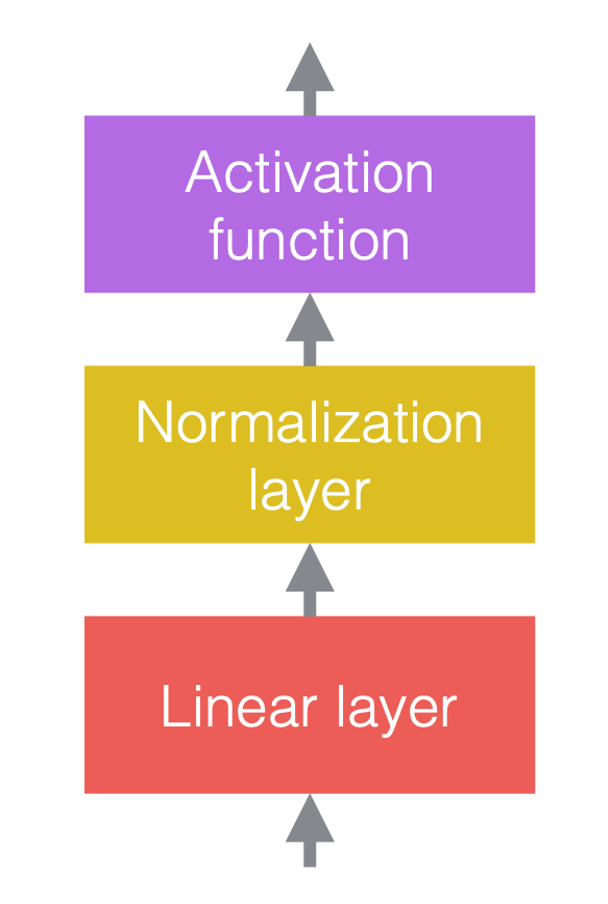
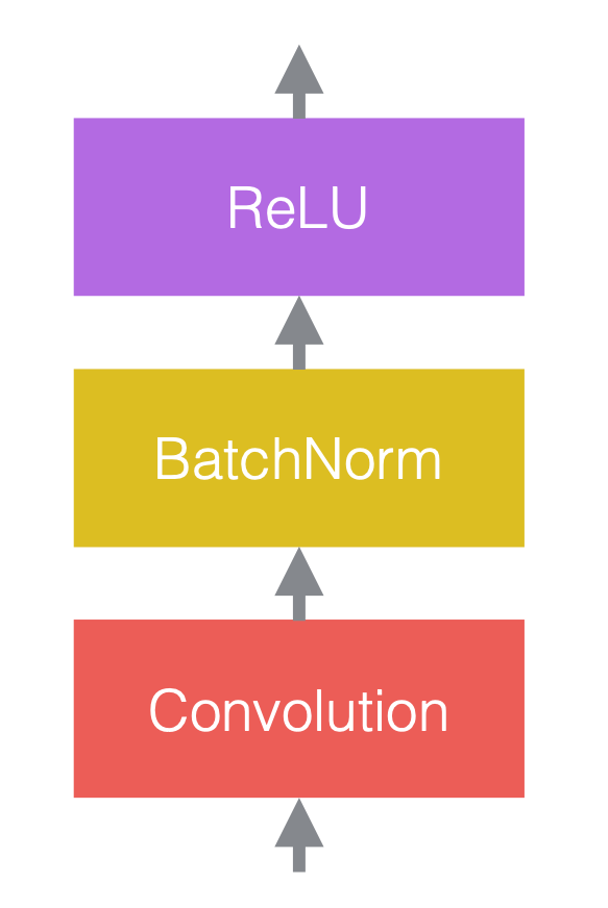
Típicamente, en las redes neuronales se utilizan alternadamente operaciones lineales y no lineales. Las operaciones no lineales, también conocidas como funciones de activación, tales como ReLU. Podemos colocar las capaz de normalización antes de las capaz lineales, o después de las funciones de activación. La práctica más común es colocarlas entre las capas lineales y las funciones de activación, como se muestra en la figura siguiente.

(a) Antes de agregar normalización	(b) Después de agregar normalización	(c) Un ejemplo en CNNs

En la figura 3(c), la convolución es la capa lineal, seguida por una normalización de lote, seguida por ReLU.

Notar que las capas de normalización afectan los datos que fluyen a través, pero no cambian la potencia de la red en el sentido que, con la apropiada configuración de los pesos, una red no normalizada puede producir las mismas salidas que una red normalizada.

Operaciones de normalización

La notación genéria para la normalización es la siguiente:

donde $x$ es el vector de entrada, y es el vector de salida, $\mu$ es la estimación de la media de $x$, $\sigma$ es la estimación de la desviación estándar de $x$, $a$ es el factor escala aprendible, y $b$ es el término sesgo aprendible.

Sin los parámetros aprendibles $a$ y $b$, la distribución del vector salida $y$ tendrá media 0 y desvío 1 fijos. El factor escala $a$ y el término sesgo $b$ mantienen el poder de representación de la red, p.e., los valores de salida pueden aún estar por encima de cualquier rango. Notar que $a$ y $b$ no deshace la normalización, porque son parametros aprendibles y mucho mas establs que $\mu$ y $\sigma$.

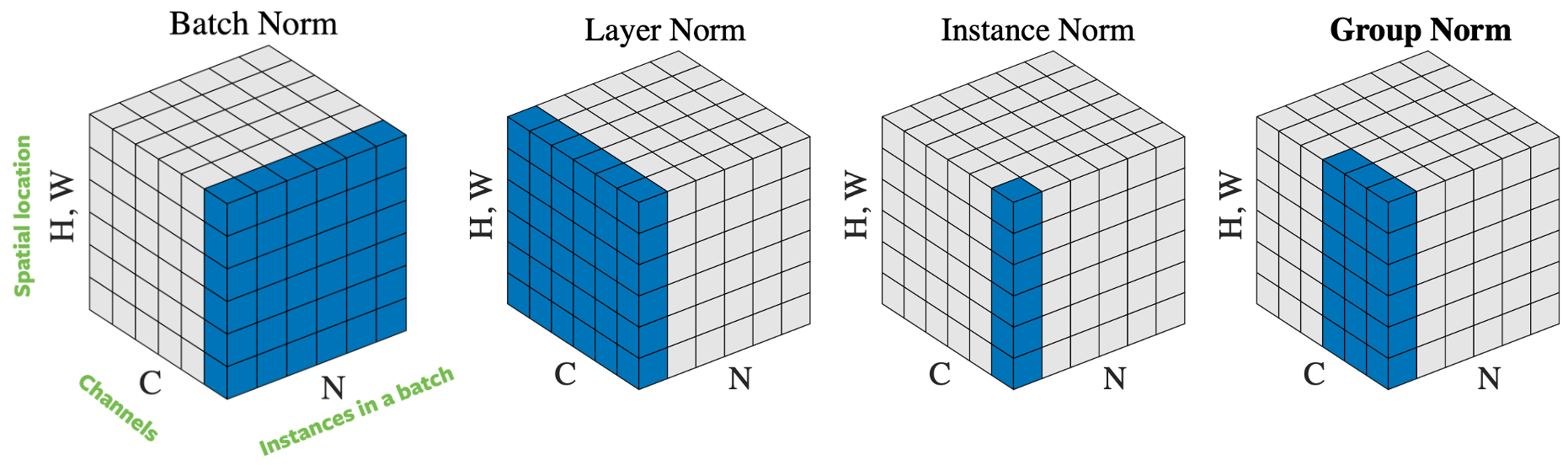
Figure 4: Operaciones de normalización.

Existen varias maneras de normalizar el vector de entrada, basándose en como se seleccionan las muestras para la normalización. La Figura 4 lista 4 formas diferentes de normalización, para un mini-lote de $N$ imágenes de alto $H$ y ancho $W$ con $C$ canales:

• Normalización de Lote (Batch norm): la normalización se aplica solo a un canal de la entrada. Este es el primer método propuesto y el más conocido. Por favor leer How to Train Your ResNet 7: Batch Norm para más información.
• Normalización de Capa (Layer norm): la normalización se aplica dentro de una imágen a través de todos los canales.
• Normalización de Instancia (Instance norm): la normalización se aplica sobre una imagen y un canal.
• Normalización de Grupo (Group Norm): la normalización es aplicada sobre una imágen pero a través de un número de canales. Por ejemplo, un grupo para los canales 0 a 9, luego el canal 10 al 19 es otro grupo, y así sucesivamente. En la práctica, el tamaño del grupo es casi siempre 32. Esta es la forma recomendada por Aaron Defazio, ya que en en la práctica tiene buena prestación y no hay conflicto con SGD. En la práctica, normalización de lotes y normalización de grupos son apropiadas para problemas de visión por computadora, mientras que para los problemas de lenguaje se usan normalización de capa y de instancia.

¿Por qué sirve la normalización?

Aunque la normalización en la práctica funciona bien, las razones detrás de su efectividad aún están en disputa. Originalmente, la normalización se propuso para reducir el “cambio en la covarianza interna”, pero algunos textos lo desaprobaron con experimentos. Sin embargo, la normalización tiene claramente la combinación de los siguientes factores:

• Las redes con normalización son más fáciles de optimizar, permitiendo el uso de tasas de aprendizaje más grandes. La normalización tiene un efecto de optimización que acelera el entrenamiento de redes neuronales.
• Las estimaciones de la media/desvío son ruidosas debido a la naturaleza aleatoria de las muestras del lote. Este ruido extra resulta a veces en mejor generalización.
• La normalización reduce la sensibilidad a los pesos iniciales.

Como resultado, la normalización permite ser un poco “descuidado” - ya que se pueden combinar bloques de redes neuronales teniendo una buena chance de entrenarla sin considerar cuan precariamente preparada puede estar la red.

Consideraciones prácticas

Es importante que la retro-propagación se hace mediante el cálculo de la media y el desvío, así como la aplicación de la normalización: de lo contrario el entrenamiento será divergente. El cálculo de la retro-propagación es bastane difícil y propenso a errores, pero Pytorch puede hacerlo automáticamente. Abajo, se listan dos clases de capa de normalización:

torch.nn.BatchNorm2d(num_features, ...)
torch.nn.GroupNorm(num_groups, num_channels, ...)

La normalización por lote fue el primer método desarrollado y el más ampliamente conocido. Sin embargo, Aaron Defazio recomienda usar normalización de grupos en su lugar. Es mas estable, teóricamente simple, y usualmente trabaja mejor. Un tamaño de grupo de 32 es un buen valor por defecto.

Notar que para la normalización por lotes y por instancia, la media/desvío quedan fijos luego del entrenamiento, en vez de ser re-calculadas cada vez que la red es evaluada, porque se necesitan múltiples muestras para la normalización. Esto no es necesario para la normalización por grupo o por capa, ya que la normalización es sobre una única muestra.

La Muerte de la Optimización

A veces, podemos incurrir en un nuevo campo donde no conocemos nada y mejorar como se hacen las cosas. Tal es el ejemplo del uso de redes neuronales para la reconstrucción de imágenes de resonancias magnéticas para acelerar su reconstrucción.

Figura 5: A veces funciona!

Reconstrucción de IRM

En el tradicional problema de la reconstrucción de imágenes de resonancias magnéticas, se toman los datos del resonador y a partir de allí se reconstruye una imágen usando un algoritmo simple. Los resonadores capturan datos en el dominio bi-dimensional de Fourier, una fila o columna cada pocos milisegundos. Estos datos crudos se componen de una frecuencia y un canal de phase. En otras palabras, puede pensarse como una imágen en el dominio complejo que tiene una parte real y un canal imaginario. Si aplicamos la transformada inversa de Fourier sobre la entrada, p.e. sumar todas las ondas seno multiplicadas por su valor, vamos a obtener como resultado la imágen anatómica.

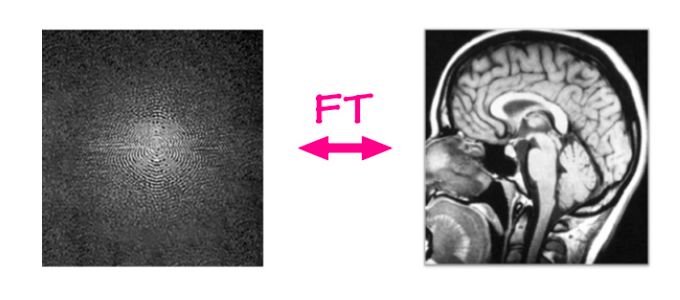
Figure 6: MRI reconstruction

Figura 6: Reconstrucción de IRM

IRM Acelerada

El nuevo problema a ser resuelto es RMI acelerada, donde por acelerada entendemos realizar el proceso de reconstrucción más rápido. Queremos hacer funcionar la máquinas más rapidamente y producir imágenes de idéntica calidad. Una manera de hacerlo, y hasta ahora la única conocida, ha sido no capturar todas las columnas del escaneo RMI. Podemos saltearnos algunas columnas aleatoriamente, aunque en la práctica es útil capturar las columnas del medio ya que contienen mucha información de la imágen, pero fuera del medio capturamos aleatoriamente. El problema, es que no podemos usar más el mapeo lineal para la reconstrucción de la imágen. La figura más a la derecha de la Figura 7 muestra la salida de un mapeo lineal aplicado al espacio de Fourier sub-muestreado. Queda claro, que este método no otorga resultados útiles, y que hay mucho lugar para hacer algo más inteligente.

Figura 7: Mapeo lineal en espacio de Fourier sub-muestreado.

Muestreo comprimido

Uno de los mayores avances en la teoría matemática durante mucho tiempo fueron los muestreos comprimidos. Un trabajo de investigación de Candes et al. mostró que teóricamente, podemos obtener una reconstrucción perfecta a partir de una imagen sub-muestreada del dominio de Fourier. En otras palabras, cuando la señal que estamos intentando reconstruir es rala o estructurada en forma rala, entonces es perfectamente posible reconstruirla con menos muestras. Pero para que esto funcione, hay requerimientos prácticos que cumplir: no necesitamos muestrea aleatoriamente, sino necesitamos muestrear incoherentemente, aunque en la práctica se termina sobre-muestreando aleatoriamente. Adicionalmente, lleva lo mismo muestrea media columna que columna entera, asi que en la práctica muestreamos columnas enteras.

Otra condición, es que necesitamos tener escasez en la imágen, donde por escasez entendemos muchos pixeles en cero o negros. La entrada cruda puede ser representada de manera escasa si aplicamos la descomposición del ancho de onda, pero aún esta descomposición nos brinda una imágen aproximadamente escasa. Por ello, este tratamiento nos brinda una reconstrucción aproximada pero no perfecta como podemos ver en la Figura 8. Sin embargo, si la imagen en el dominio del ancho de onda fuera escasa, entonces obtendríamos una imágen perfecta.

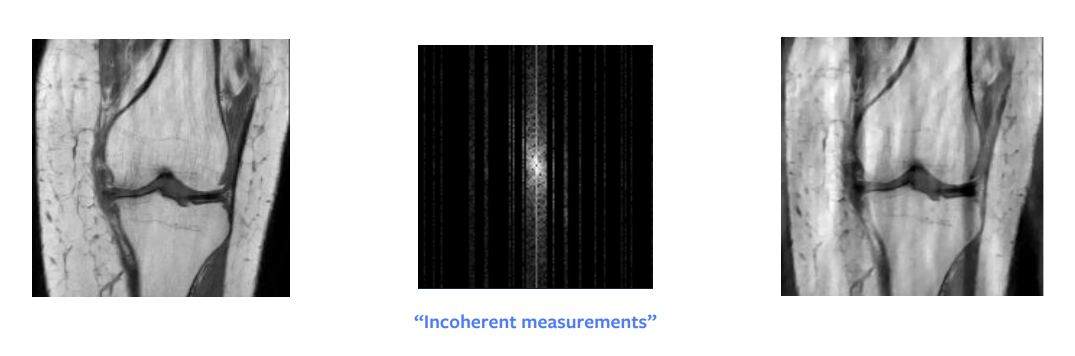
Figura 8: Muestreo comprimido

El muestreo comprimido está basado en la teoría de la optimización. La manera en la que podemos obtener la reconstrucción es mediante la resolución de un mini-problema de optimización el cuál tiene un termino de regularización adicional:

donde $M$ es la función máscara que pone a cero elementos no muestreados, $\mathcal{F}$ es la transformada de Fourier, $y$ son los datos observados en el dominio de Fourier, $\lambda$ es la fuerza de la penalización de la regularización, y $V$ es la función de regularización.

El problema de optimización debe ser resuelto para cada paso o cada “rebanada” de un escaneo IRM, que a menudo tarda más que el escaneo en sí mismo. Esto nos dá otra razón para encontrar una mejor solución.

Quién necesita optimización?

En vez de resolver un pequeño problema de optimización con cada paso del tiempo, por qué no usar una red neuronal grande para producir la solución requerida directamente? Nuestra esperanza es que podemos entrenar una red neuronal lo suficientemente compleja que resuelva el problema de optimización en un solo paso y que produce una salida que es tan buena como la solución obtenida mediante resolver el problema de optimización a cada paso.

donde $B$ es nuestro modelo de aprendizaje profundo y $y$ son los datos observados en el dominio de Fourier.

Hace 15 años, esto era dificultoso, pero hoy en día es mucho mas fácil de implementar. La figura 9 muestra el resultado de la aplicación de aprendizaje profundo a este problema, y podemos ver que esta salida es mucho mejor que la salida utilizando muestreo comprimido y parece muy similar al escaneo real.

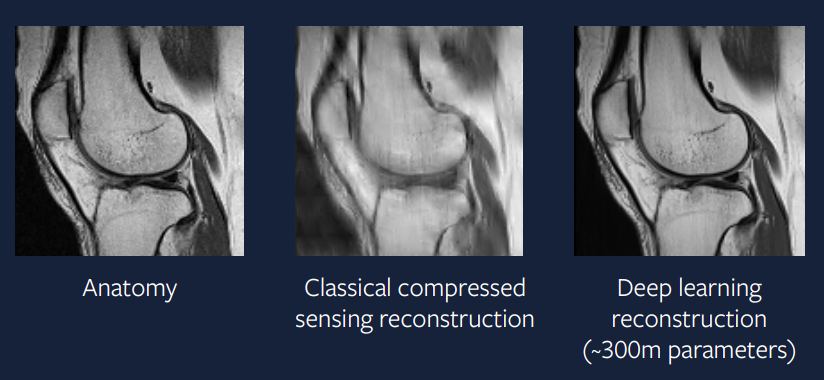
Figure 9: Enfoque Aprendizaje Profundo

El modelo utilizado para generar esta reconstrucción utiliza el optimizador ADAM, capas de normalización de grupo, y una red convolucional basada en U-Net. Tal enfoque es muy similar a las aplicaciones prácticas y en pocos años estaremos viendo estos escaneos IRM en la práctica clínica con seguridad. –>