Técnicas de Optimización I

Descenso de gradiente

Comenzamos nuestro estudio de los Métodos de Optimización con el método más básico y el peor de todos (como veremos): Descenso de Gradiente.

Problema:

Solución Iterativa:

donde,

• $w_{k+1}$ es el valor actualizado luego de $k$ iteraciones,
• $w_k$ es el valor inicial antes de la iteración $k$-ésima,
• $\gamma_k$ es el tamaño de paso,
• $\nabla f(w_k)$ es el gradiente de $f$.

La suposición aquí es que la función $f$ es continua y diferenciable. Nuestro objetivo es encontrar el punto más bajo (valle) de la función de optimización. Sin embargo, la dirección real a este valle no se conoce. Solo podemos observar localmente y, por lo tanto, la dirección del gradiente negativo es la mejor información que tenemos. Dar un pequeño paso en esa dirección solo puede acercarnos al mínimo. Una vez que hemos dado el pequeño paso, calculamos el nuevo gradiente y volvemos a movernos una pequeña cantidad en esa dirección, hasta llegar al valle. Por lo tanto, esencialmente todo lo que hace el descenso de gradiente es seguir la dirección del descenso más pronunciado (gradiente negativo).

El parámetro $\gamma$ en la ecuación de actualización iterativa se llama tamaño de paso. Generalmente no conocemos el valor del tamaño de paso óptimo; entonces tenemos que probar diferentes valores. La práctica estándar es probar un montón de valores en una escala logarítmica y luego usar el mejor. Hay distintos escenarios que pueden ocurrir. La imagen de arriba muestra estos escenarios para una cuadrática en 1D. Si el valor de la tasa de aprendizaje es demasiado bajo, haríamos un progreso constante hacia el mínimo. Sin embargo, esto puede llevar más tiempo del ideal. En general, es muy difícil (o imposible) obtener un tamaño de paso que nos lleve directamente al mínimo. Lo que idealmente querríamos es tener un tamaño de paso un poco más grande que el óptimo. En la práctica, esto proporciona la convergencia más rápida. Sin embargo, si usamos una tasa de aprendizaje demasiado grande, las iteraciones nos alejarán cada vez más del mínimo y resultará en divergencia. En la práctica, nos gustaría utilizar una tasa de aprendizaje que sea ligeramente menor a la divergente.

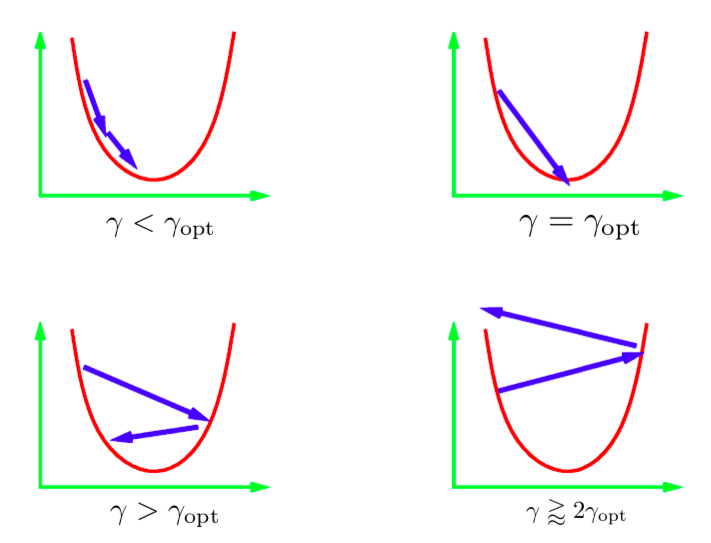
Figura 1: Tamaño de paso para cuadrática en 1D

Descenso de Gradiente Estocástico

En el Descenso de Gradiente Estocástico (SGD), reemplazamos el vector de gradiente real con una estimación estocástica del vector de gradiente. Específicamente para una red neuronal, la estimación estocástica hace referencia al gradiente del error para un único punto de datos (instancia única).

Sea $f_i$ el error de la red para la $i$-ésima instancia.

La función que eventualmente queremos minimizar es $f$, el error total sobre todas las instancias.

En SGD, actualizamos los pesos de acuerdo con el gradiente sobre $f_i$ (a diferencia del gradiente sobre el error total $f$).

\(\begin{aligned} w_{k+1} &= w_k - \gamma_k \nabla f_i(w_k) & \quad\text{(i elegido uniformemente al azar)} \end{aligned}\)

Si $i$ es elegido al azar, entonces $f_i$ es un estimador ruidoso pero insesgado de $f$, que se escribe matemáticamente como:

Como resultado de esto, el $k$-ésimo paso esperado de SGD es el mismo que el $k$-ésimo de Descenso de Gradiente completo:

Por lo tanto, cualquier actualización de SGD es lo mismo, en esperanza, que la actualización de lote completo (full batch). Sin embargo, SGD no es solo un descenso de gradiente más rápido con ruido. Además de ser más rápido, SGD también puede obtener mejores resultados que el descenso de gradiente de lote completo. El ruido en SGD puede ayudarnos a evitar los mínimos locales poco profundos y a encontrar mejores mínimos (más profundos). Este fenómeno es llamado annealing.

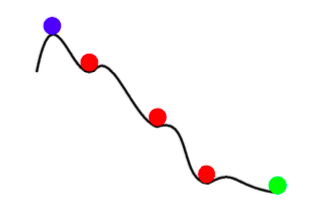
Figura 2: *Annealing* con SGD

En resumen, las ventajas del Descenso de Gradiente Estocástico son las siguientes:

1. Hay mucha información redundante en todas las instancias. SGD evita muchos de estos cálculos redundantes.
2. En las primeras etapas, el ruido es pequeño en comparación con la información en el gradiente. Por lo tanto, un paso SGD es prácticamente tan bueno como un paso de GD.
3. Annealing - El ruido en la actualización de SGD puede evitar la convergencia a un mínimo local malo (superficial).
4. El Descenso de Gradiente Estocástico es drásticamente más barato de calcular (ya que no utiliza todos los puntos de datos, sino solo uno, en cada cálculo del gradiente).

Mini-batching

En mini-batching, consideramos el error usando varias instancias de datos seleccionadas al azar en lugar de calcularlas en una sola instancia. Esto reduce el ruido en cada actualización.

A menudo podemos hacer un mejor uso de nuestro hardware mediante mini-batches en lugar de una sola instancia. Por ejemplo, las GPU se utilizan de manera ineficiente cuando utilizamos entrenamiento de instancia única. Las técnicas de entrenamiento en redes distribuidas dividen un gran mini-batch entre las máquinas de un clúster y luego suman los gradientes resultantes. Facebook recientemente entrenó una red con los datos de ImageNet en una hora, utilizando entrenamiento distribuido.

Es importante tener en cuenta que el descenso de gradiente nunca debe usarse con lotes de tamaño completo. En caso de que se quiera entrenar en el lote completo, debe usarse una técnica de optimización llamada LBFGS. PyTorch y SciPy proporcionan implementaciones de esta técnica.

Momentum

En Momentum, tenemos dos parámetros iterables ($p$ y $w$) en lugar de solo uno. Se actualizan de la siguiente manera:

$p$ se llama el impulso (momentum) de SGD. En cada paso de actualización, sumamos el gradiente estocástico al valor anterior del impulso, después de reducirlo por un factor $\beta$ (valor entre 0 y 1). $p$ puede considerarse como un promedio continuo de los gradientes. Finalmente, movemos $w$ en la dirección del nuevo impulso $p$.

Forma alternativa: Método Estocástico de Bola Pesada

Esta forma es matemáticamente equivalente a la anterior. Aquí, el siguiente paso es una combinación de la dirección del paso anterior ($w_k - w_{k-1}$) y el nuevo gradiente negativo.

Intuición

SGD Momentum es similar al concepto de impulso en física. El proceso de optimización se asemeja a una bola pesada rodando cuesta abajo. Momentum mantiene la pelota en movimiento en la misma dirección en la que ya se está moviendo. El gradiente puede considerarse como una fuerza que empuja la pelota en otra dirección.

Figura 3: Efecto de Momentum
Fuente: distill.pub

En lugar de hacer cambios dramáticos en la dirección de movimiento (como en la figura de la izquierda), el impulso produce cambios modestos. Momentum amortigua las oscilaciones que son comunes cuando solo usamos SGD.

El parámetro $\beta$ se llama Factor de Amortiguación. $\beta$ tiene que ser mayor que cero, porque de ser igual a cero, solo se estaría calculando un descenso de gradiente. También tiene que ser menor que 1, de lo contrario todo explotará. Los valores más pequeños de $\beta$ resultan en cambios de dirección más pronunciados. Para valores más grandes, toma más tiempo cambiar de dirección.

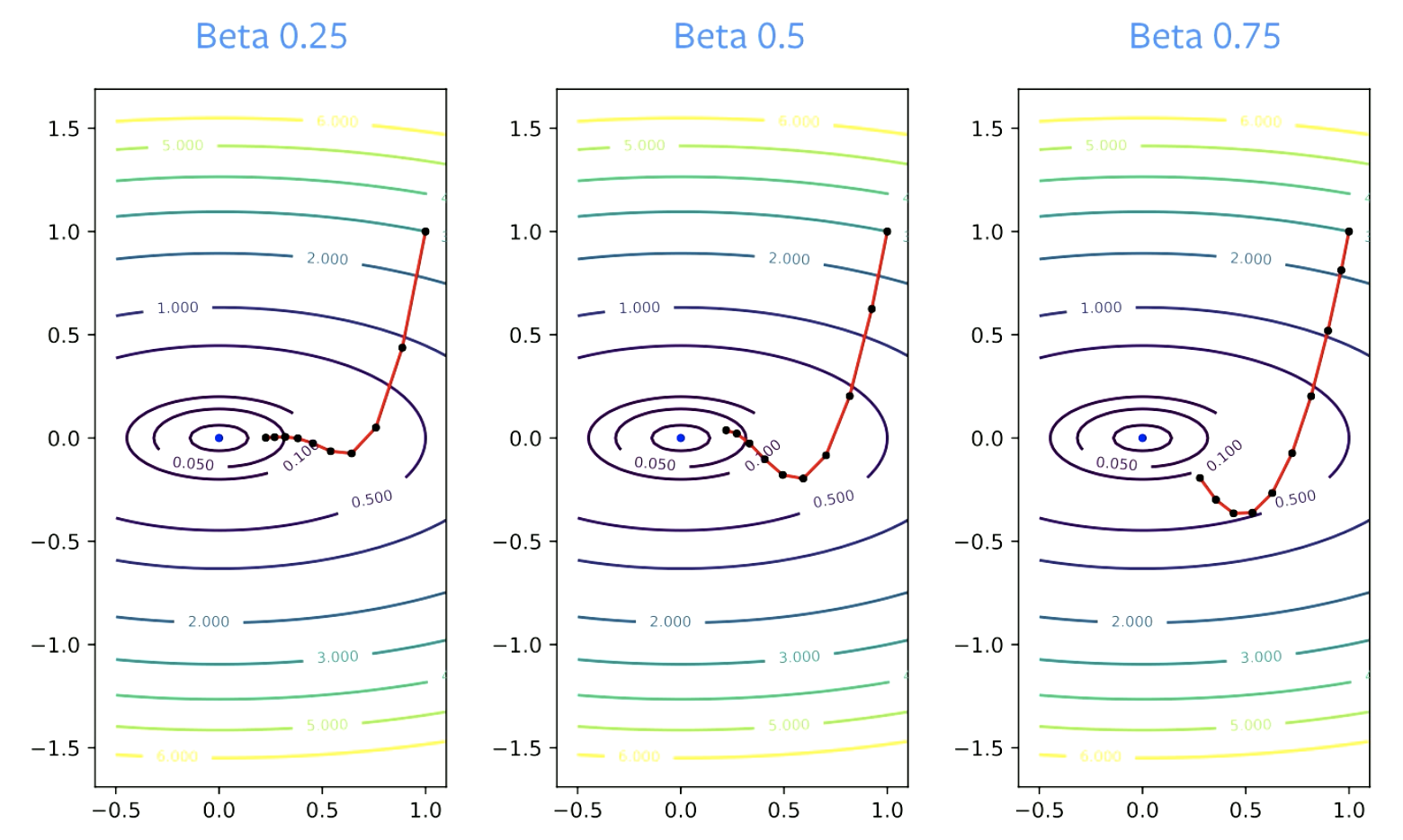
Figura 4: Efecto de Beta en la convergencia

Pautas prácticas

Momentum debe usarse casi siempre con descenso de gradiente estocástico. $\beta$ = 0.9 ó 0.99 suele funcionar bien.

El valor del parámetro de tamaño de paso generalmente debe disminuirse cuando se aumenta el parámetro de impulso para mantener la convergencia. Si $\beta$ cambia de 0.9 a 0.99, el valor de la tasa de aprendizaje debe reducirse en un factor de 10.

¿Por qué funciona Momentum?

Aceleración

Las siguientes son las reglas de actualización para el impulso de Nesterov.

Con el impulso de Nesterov, puede obtenerse una convergencia acelerada si se eligen las constantes con mucho cuidado. Pero esto solo se aplica a problemas convexos y no a redes neuronales.

Mucha gente dice que el impulso normal también es un método acelerado. Pero en realidad, se acelera solo para las funciones cuadráticas. Además, la aceleración no funciona bien con SGD, ya que SGD tiene ruido y la aceleración no funciona bien con ruido. Por lo tanto, aunque hay un poco de aceleración con Momentum SGD, por sí solo no es una buena explicación del alto rendimiento de la técnica.

Suavisado del ruido

Probablemente, una razón más práctica y probable de por qué Momentum funciona es el suavizado del ruido.

Momentum promedia gradientes. Es un promedio continuo de gradientes que utilizamos para cada actualización en cada paso.

Teóricamente, para que SGD funcione, deberíamos tomar el promedio de todas las actualizaciones de los pasos.

Lo mejor acerca de SGD con Momentum es que este promedio ya no es necesario. Momentum agrega un suavizado al proceso de optimización, lo que hace que cada actualización sea una buena aproximación a la solución. Con SGD, se querría promediar un montón de actualizaciones y luego dar un paso en esa dirección.

Tanto la aceleración como el suavizado del ruido contribuyen al alto rendimiento de Momentum.

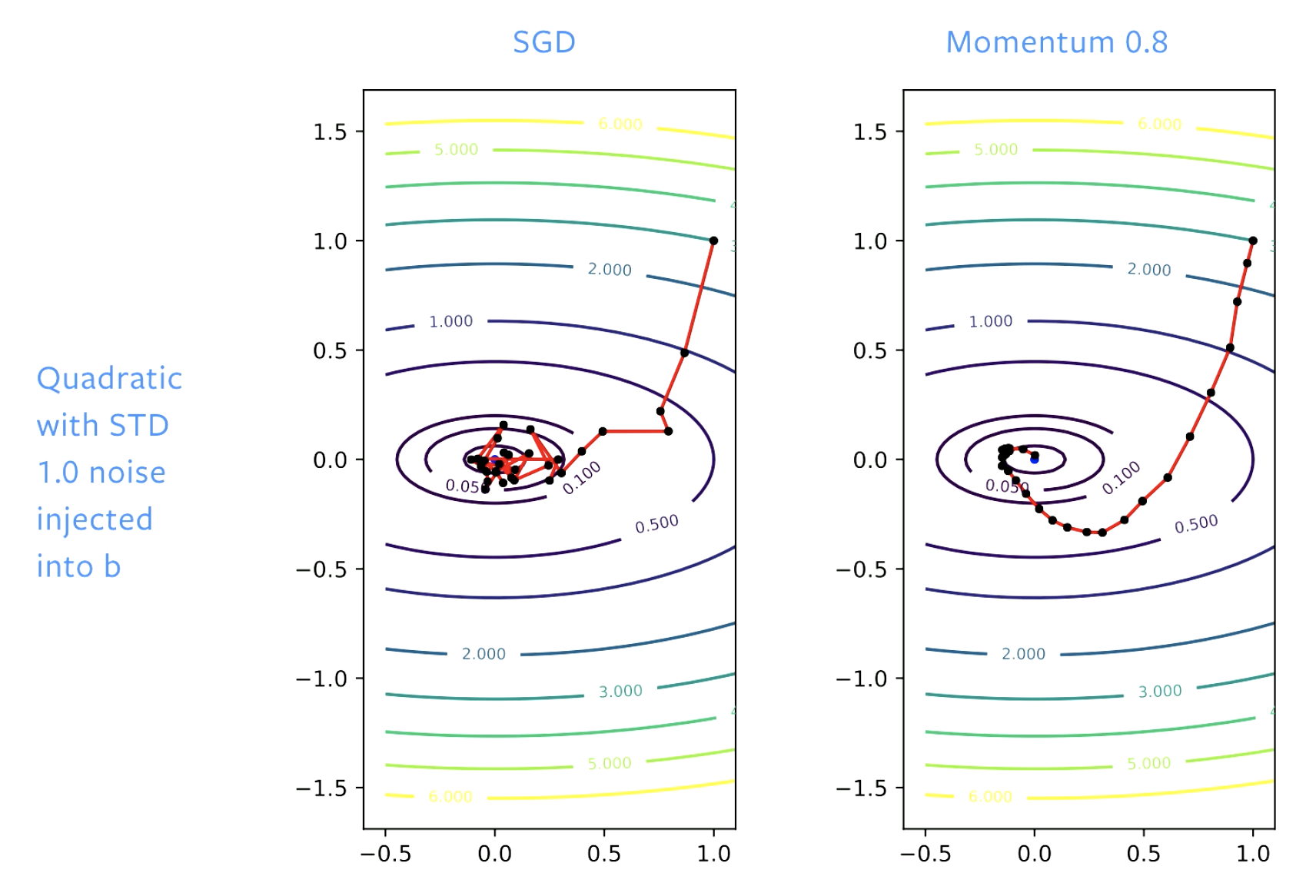
Figura 5: SGD vs. Momentum

Con SGD, inicialmente hacemos un buen progreso hacia la solución, pero cuando llegamos al tazón (fondo del valle) nos quedamos rebotando en este piso. Si ajustamos la tasa de aprendizaje de manera acorde, rebotaremos menos. Con Momentum suavizamos los pasos, y con esto se logra que no haya rebotes.