Álgebra lineal y convoluciones

🎙️ Alfredo Canziani

Repaso de álgebra lineal

Esta parte es un repaso de álgebra lineal básica dentro del contexto de las redes neuronales. Empezamos con una capa oculta simple $\boldsymbol{h}$:

\[\boldsymbol{h} = f(\boldsymbol{z})\]

La salida es una función no lineal $f$ aplicada a un vector $z$. Aquí, $z$ es la salida de una transformación afín $\boldsymbol{A} \in\mathbb{R^{m\times n}}$ al vector de entrada $\boldsymbol{x} \in\mathbb{R^n}$:

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

Para simplificar, ignoraremos los términos constantes (bias). Podemos desarrollar la función lineal del siguiente modo:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

donde $\boldsymbol{a}^{(i)}$ es la $i$-ésima fila de la matriz $\boldsymbol{A}$.

Para entender el significado de esta transformación, analizaremos una componente de $\boldsymbol{z}$ tal que $a^{(1)}\boldsymbol{x}$. Para $n=2$, $\boldsymbol{a} = (a_1,a_2)$ y $\boldsymbol{x} = (x_1,x_2)$.

$\boldsymbol{a}$ y $\boldsymbol{x}$ pueden dibujarse como vectores en los ejes de coordenados de $\mathbb{R^2}$. Ahora, si el ángulo entre $\boldsymbol{a}$ y $\hat{\boldsymbol{\imath}}$ es $\alpha$ y el ángulo entre $\boldsymbol{x}$ y $\hat{\boldsymbol{\imath}}$ es $\xi$, entonces con trigonometría $a^\top\boldsymbol{x}$ puede desarrollarse como:

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

La salida mide la alineación de la entrada con una fila específica de la matriz $\boldsymbol{A}$. Esto se puede entender observando el ángulo entre los dos vectores, $\xi-\alpha$. Cuando $\xi = \alpha$, los dos vectores están perfectamente alineados y se obtiene el máximo. Si $\xi - \alpha = \pi$, entonces $\boldsymbol{a}^\top\boldsymbol{x}$ alcanza su mínimo y los dos vectores están apuntando en direcciones opuestas. En esencia, la transformación lineal permite ver la proyección de una entrada a varias orientaciones definidas por $A$. Esta intuición aplica en dimensiones superiores.

Otra forma de entender la transformación lineal es entendiendo que $\boldsymbol{z}$ también puede desarrollarse como:

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

La salida es la suma ponderada de las columnas de la matriz $\boldsymbol{A}$. Por lo tanto, la señal no es más que una composición de la entrada.

Extender álgebra lineal a convoluciones

Ahora extenderemos el álgebra lineal a convoluciones, usando un ejemplo de análisis de datos de audio. Empezamos representando una capa totalmente conectada como una matriz de multiplicación:

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

En este ejemplo, la matriz de pesos tiene un tamaño de $4 \times 3$, el vector de entrada tiene un tamaño de $3 \times 1$ y el vector de salida tiene un tamaño $4 \times 1$.

Sin embargo, para datos de audio, los datos de mucha mayor longitud (no de tres muestras de longitud). El número de muestras en los datos de audio es igual a la duración del audio(por ejemplo, tres segundos) por la tasa de muestreo (por ejemplo, 22.05 kHz). Como se muestra a continucación, el vector de entrada $\boldsymbol{x}$ será muy grande. Así pues, la matriz de pesos será más “ancha”.

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

La formulación anterior será difícil de entrenar. Afortunadamente, hay maneras de simplificar esto.

Propiedad: localidad

Debido a la localidad (es decir, no nos importan los puntos lejanos) de los datos, $w_{1k}$ de la matriz de pesos anterior, pueden sustituirse con 0 cuando $k$ es relativamente grande. Por lo tanto, la primera fila de la matriz se convierte en un kernel de dimensión tres. Llamaremos a este kernel de dimensión tres $\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$.

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Propiedad: estacionariedad

Los datos de señales naturales poseen la propiedad de estacionariedad (es decir, ciertos patrones se repetirán). Esto nos ayuda a reusar el kernel $\mathbf{a}^{(1)}$ que definimos previamente. Usamos este kernel colocándolo una posición más lejos a la vez (es decir, con una zancada (stride) de uno), lo que resulta en lo siguiente:

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

La parte superior derecha y la parte inferior izquierda de la matriz se sustituyen por $0$ gracias a la localidad, lo que lleva a su dispersión (mayoría ceros). El reusar ciertos kernels una y otra vez es conocido como compartir pesos.

Múltiples capas de la matriz de Teoplitz

Después de estos cambios, el número de parámetros que nos quedan es tres (es decir, $a_1,a_2,a_3$). En comparación con la matriz de pesos anterior, que tenía 12 parámetros (es decir, $w_{11},w_{12},\cdots,w_{43}$), el número actual de parámetros es demasiado restrictivo y nos gustaría ampliarlo.

A la matriz anterior se le puede considerar una capa (es decir, una capa convolucional) con el kernel $\boldsymbol{a}^{(1)}$. Entonces podemos construir múltiples capas con diferentes kernels $\boldsymbol{a}^{(2)}$, $\boldsymbol{a}^{(3)}$, etc, para incrementar el número de parámetros.

Cada capa tiene una matriz que contiene solo un kernel, que es copiado múltiples veces. A este tipo de matriz se le llama matriz de Toeplitz. En cada matriz de Toeplitz, cada diagonal descendente de izquierda a derecha es constante. Las matrices de Toeplitz que usamos aquí también son matrices dispersas.

Dado el primer kernel $\boldsymbol{a}^{(1)}$ y el vector de entrada $\boldsymbol{x}$, la primera posición de la salida dada por esta capa es $a_1^{(1)} x_1 + a_2^{(1)} x_2 + a_3^{(1)}x_3$. Por lo tanto, el vector de salida completo tendrá la forma siguiente:

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

Se puede aplicar el mismo método de multiplicación de matrices en las siguientes capas convolucionales con otros kernels (por ejemplo, $\boldsymbol{a}^{(2)}$ y $\boldsymbol{a}^{(3)}$) para obtener resultados similares.

Escuchando convoluciones - Jupyter Notebook

Puedes encontrar el Jupyter Notebook aquí.

En este cuaderno, vamos a explorar la convolución como “un producto escalar móvil”.

La biblioteca librosa nos permite cargar un segmento de audio $\boldsymbol{x}$ y su frecuencia de muestreo. En este caso, hay 70 641 muestras, la tasa de muestreo es 22.05 kHz y la longitud total del segmento de audio es 3.2 s. La señal de audio importada es ondulada (ver la figura 1) y podemos suponer cómo suena por la amplitud del eje $y$. La señal de audio $x(t)$ es, en realidad, el sonido que suena cuando apagas el sistema operativo Windows (ver la figura 2).

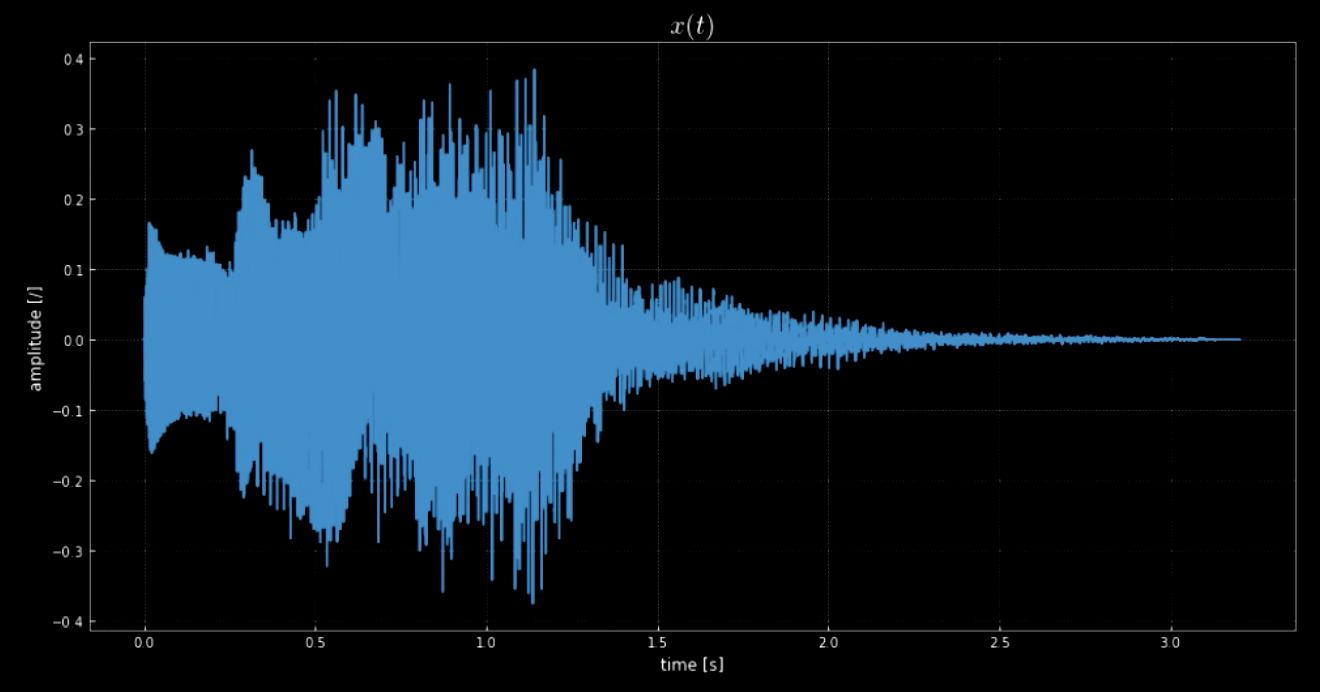
Fig. 1: Visualización de la señal de audio

Fig. 2: Notas de la señal de audio anterior

Necesitamos separar las notas de la forma de onda. Para conseguirlo, si usamos la transformada de Fourier (FT, por sus siglas en inglés), todas las notas saldrían juntas y sería difícil determinar el momento exacto y la ubicación de cada tono. Por lo tanto, se necesita una FT localizada (también conocida como espectrograma). Como se observa en el espectrograma (ver la figura 3), diferentes tonos alcanzan su máxima frecuencia (por ejemplo, el primer tono llega a su máximo en en 1 600). El concatenar los cuatro tonos en sus frecuencias nos da una versión de tono de la señal original.

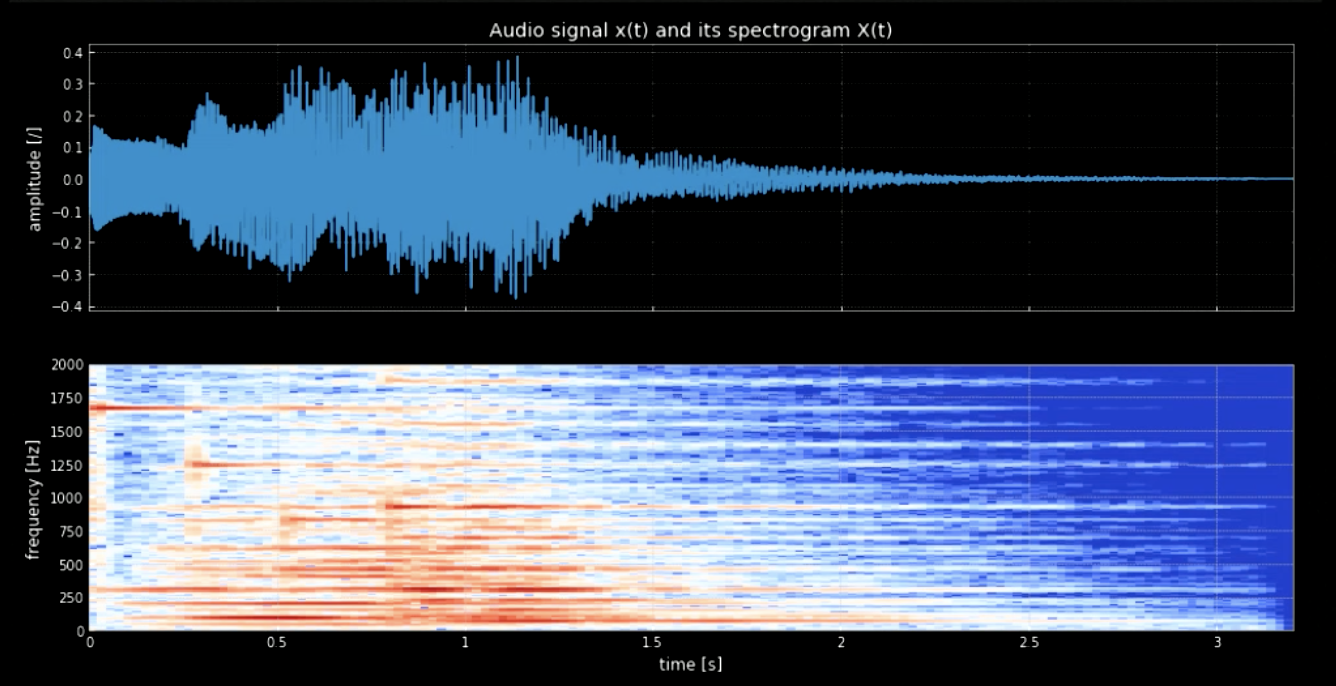
Fig. 3: Señal de audio y su espectrograma

La convolución de la señal de entrada con todos los tonos (por ejemplo, todas las teclas del piano) puede ayudar a extraer todas las notas en la pieza de entrada (es decir, los resultados cuando el audio coincide con kernels específicos). Los espectrogramas de la señal original y la señal de los tonos concatenados se muestran en la figura 4 mientras que las frecuencias de la señal original y los cuatro tonos se muestran en la figura 5. La gráfica de la convolución de los cuatro kernels con la señal de entrada (señal original) se muestra en la figura 6. La figura 6 junto con los clips de audio de las convoluciones prueban la efectividad de las convoluciones para extraer las notas.

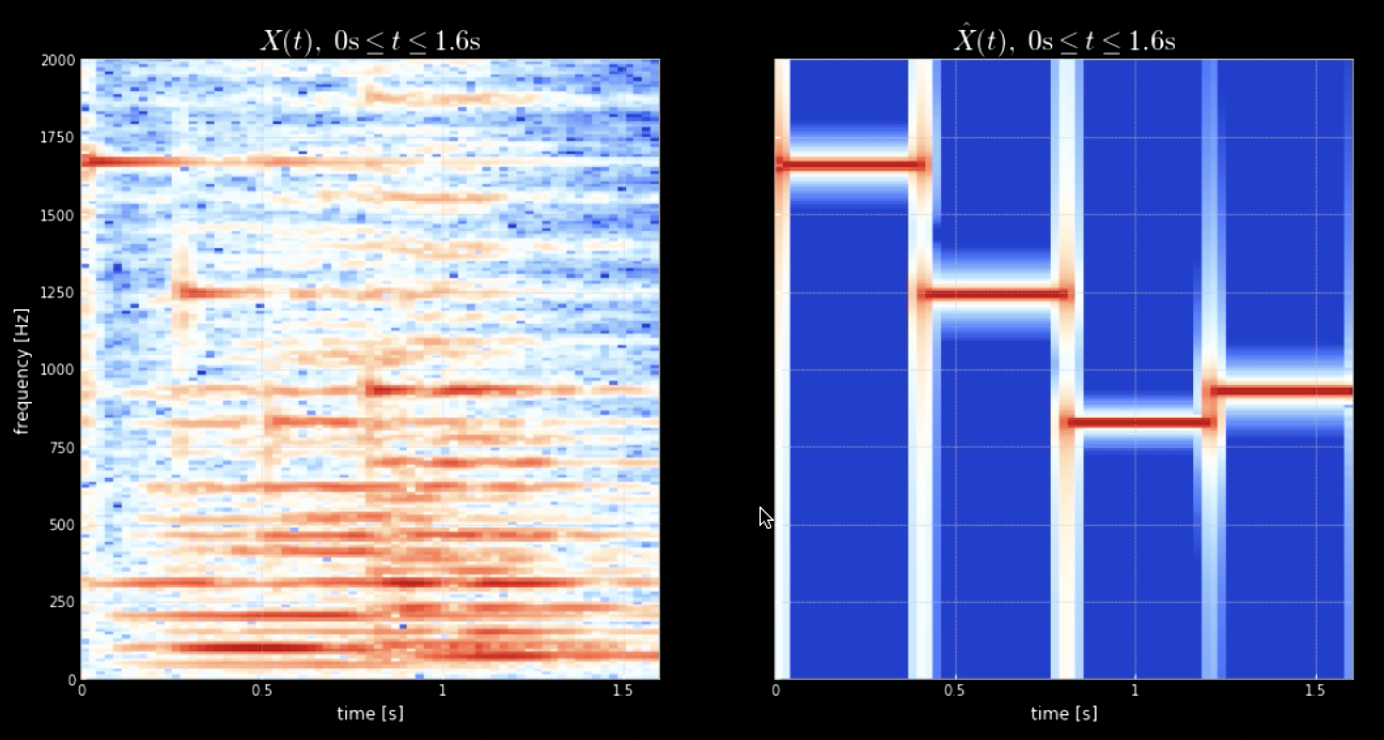
Fig. 4: Espectrograma de la señal original (izquierda) y espectrograma de la concatenación de tonos (derecha)

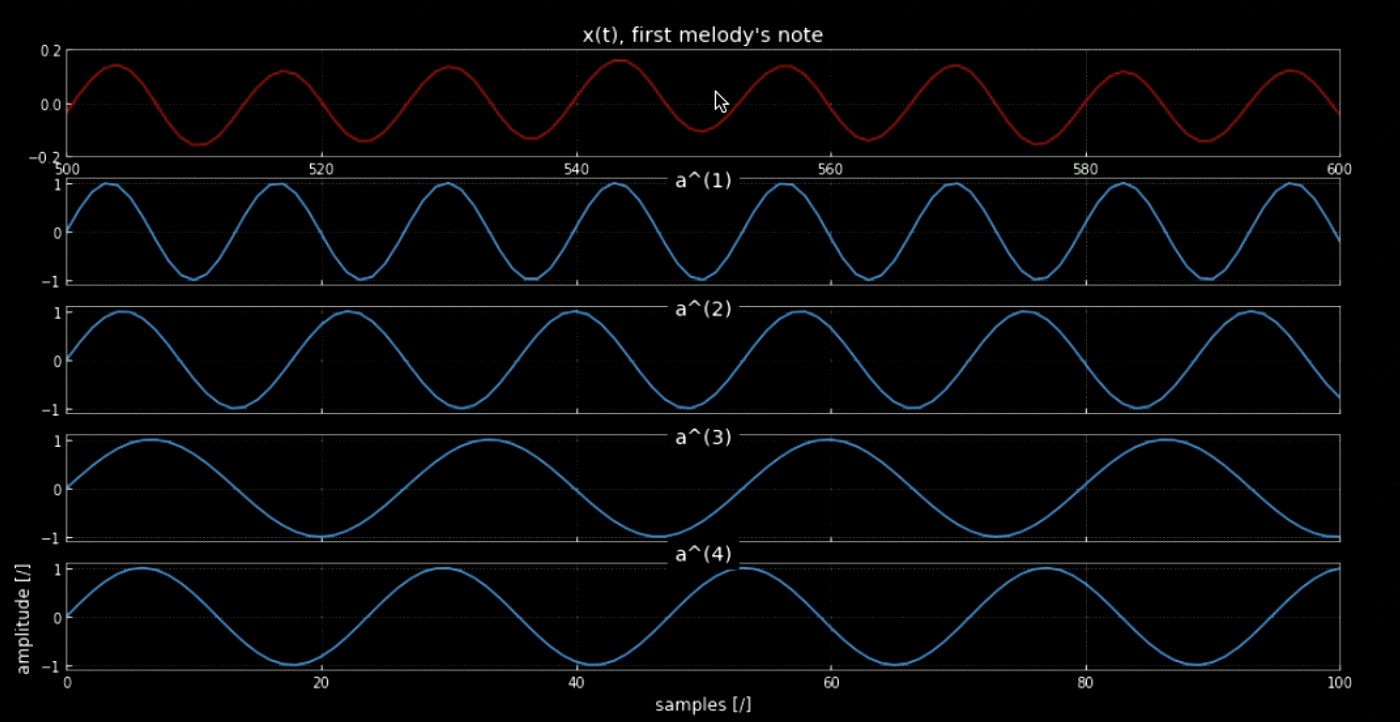
Fig. 5: Primera nota de la melodía

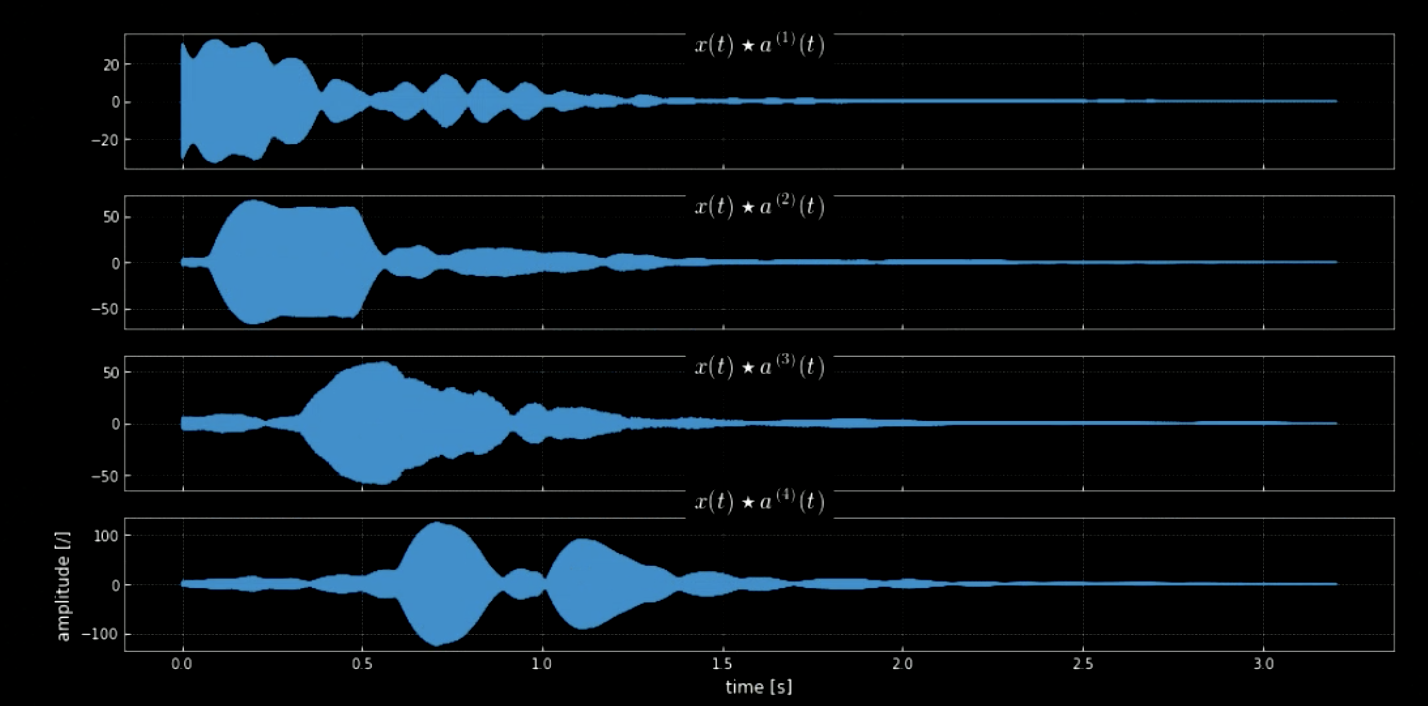
Fig. 6: Convolución de cuatro kernels

Dimensionalidad de los diferentes conjuntos de datos

La última parte es una pequeña digresión sobre las diferentes representaciones de la dimensionalidad y ejemplos de lo mismo. Aquí consideramos que el conjunto de entrada $X$ está formado por funciones de mapeado del dominio $\Omega$ hacia los canales $c$.

Ejemplos

• Datos de audio: el dominio es unidimensional, señal discreta indexada en el tiempo; número de canales $c$ puede variar desde 1 (mono), 2 (estéreo), 5+1 (Dolby 5.1), etc.
• Datos de imagen: el dominio es bidimensional (pixeles); $c$ pueden variar desde 1 (escala de grises), 3 (color), 20(hiperespectral), etc.
• Relatividad especial: el dominio es $\mathbb{R^4} \times \mathbb{R^4}$ (espacio-tiempo $\times$ cuatro-momentum); cuando $c = 1$ es conocido como Hamiltoniano.

Fig. 7: Diferentes dimensiones de diferentes tipos de señales

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
Manuel Pinar-Molina
18 Feb 2020