Propiedades de las señales naturales
🎙️ Alfredo CanzianiPropiedades de las señales naturales
Todas las señales pueden considerarse como vectores. Por ejemplo, una señal de audio es una señal unidimensional $\boldsymbol{x} = [x_1, x_2, \cdots, x_T]$ donde cada valor $x_t$ representa la amplitud de la forma de onda en el tiempo $t$. Para dar sentido a lo que alguien está hablando, nuestra cóclea primero convierte las vibraciones de la presión del aire en señales y luego el cerebro usa un modelo de lenguaje para convertir esta señal a un idioma, es decir, necesita elegir el enunciado más probable, dada la señal. En la música, la señal es estereofónica, o sea que tiene dos o más canales para dar la ilusión de que el sonido proviene de múltiples direcciones. Aunque tenga dos canales, sigue siendo una señal unidimensional porque el tiempo es la única variable a lo largo de la cual está cambiando la señal.
Una imagen es una señal bidimensional porque la información se representa espacialmente. Hay que tener en cuenta que cada punto puede ser un vector en sí mismo. Esto significa que si tenemos $d$ canales en una imagen, cada punto espacial en la imagen es un vector de dimensión $d$. Una imagen en color tiene planos RGB, lo que significa que $d = 3$. Para cualquier punto $x_{i,j}$, esto corresponde a la intensidad de los colores rojo, verde y azul, respectivamente.
Incluso podemos representar el lenguaje con la lógica anterior. Cada palabra corresponde a un vector one-hot, con un uno en la posición en la que se encuentra en nuestro vocabulario y ceros en el resto. Esto significa que cada palabra es un vector del tamaño del vocabulario.
Las señales de datos naturales siguen estas propiedades:
- Estacionariedad: Ciertos patrones se repiten a lo largo de una señal. En las señales de audio, observamos el mismo tipo de patrones una y otra vez en todo el dominio temporal. En imágenes, esto significa que podemos esperar que se repitan patrones visuales similares a través de la dimensionalidad.
- Localidad: Los puntos cercanos están más correlacionados que los puntos lejanos. Para la señal unidimensional, esto significa que si observamos un pico en algún punto $t_i$, esperamos que los puntos en una pequeña ventana alrededor de $t_i$ tengan valores similares a $t_i$, pero para un punto $t_j$ lejos de $t_i$, $x_{t_i}$ tiene muy poca relación con $x_{t_j}$. Más formalmente, la convolución entre una señal y su contraparte invertida tiene un pico cuando la señal se superpone perfectamente con su versión invertida. Una convolución entre dos señales unidimensionales (correlación cruzada) no es más que su producto punto, que es una medida de cuán similares o cercanos son los dos vectores. Por lo tanto, la información está contenida en porciones y partes específicas de la señal. Para las imágenes, esto significa que la correlación entre dos puntos en una imagen disminuye a medida que alejamos los puntos. Si el pixel $x_{0,0}$ es azul, la probabilidad de que el próximo pixel ($x_{1,0}, x_{0,1}$) también sea azul es bastante alta, pero a medida que se avanza hacia el extremo opuesto de la imagen ($x_{-1,-1}$), el valor de este pixel será independiente del valor de pixel en $ x_{0,0}$.
- Composicionalidad: todo en la naturaleza está compuesto de partes que se componen de subpartes, y así sucesivamente. Por ejemplo, los caracteres forman cadenas que forman palabras, que luego forman oraciones. Las oraciones se pueden combinar para formar documentos. La composicionidad permite que el mundo sea explicable.
Si nuestros datos exhiben estacionariedad, localidad y composicionalidad, podemos explotarlos con redes que utilicen dispersión, parámetros compartidos y apilamiento de capas.
Explotando propiedades de las señales naturales para generar invariancia y equivalencia
Localidad $\Rightarrow$ dispersión
La figura 1 muestra una red de cinco capas fully connected. Cada flecha representa un peso que se multiplicará por las entradas. Como podemos ver, esta red es computacionalmente costosa.
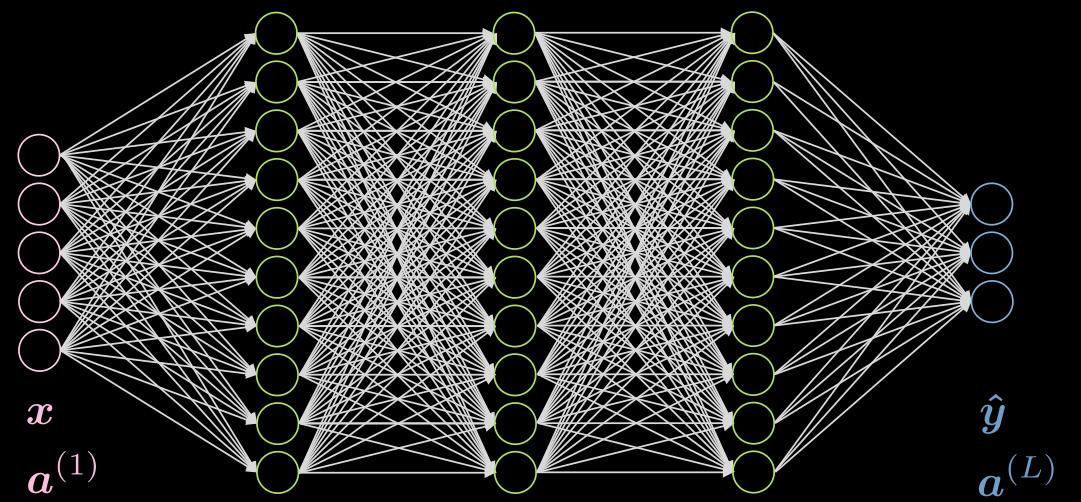
Figura 1: Red *Fully Connected*
Si nuestros datos exhiben localidad, cada neurona necesita estar conectada a solo unas pocas neuronas locales de la capa anterior. Por lo tanto, algunas conexiones se pueden ignorar, como se muestra en la figura 2. La figura 2(a) representa una red FC. Aprovechando la propiedad de localidad de nuestros datos, eliminamos las conexiones entre neuronas lejanas como se ve en la figura 2(b). Aunque las neuronas de la capa oculta (verde) en la figura 2(b) no abarcan toda la entrada, la arquitectura general podrá considerar todas las neuronas de entrada. El campo receptivo (RF, por sus siglas en inglés) es el número de neuronas de capas anteriores que cada neurona de una capa en particular puede ver o ha tenido en cuenta. Por lo tanto, el RF de la capa de salida con respecto a la capa oculta es tres, el RF de la capa oculta con respecto a la capa de entrada es tres, pero el RF de la capa de salida con respecto a la capa de entrada es cinco.
| Before Applying Sparsity.png) |
|  After Applying Sparsity.png) |
|Figura 2(a): Antes de aplicar dispersión | Figura 2(b): Luego de aplicar dispersión|
|
|Figura 2(a): Antes de aplicar dispersión | Figura 2(b): Luego de aplicar dispersión|
Estacionariedad $\Rightarrow$ parámetros compartidos
Si nuestros datos muestran estacionariedad, podríamos usar un pequeño conjunto de parámetros varias veces en la arquitectura de red. Por ejemplo, en nuestra red dispersa, (ver la figura 3(a)), podemos usar un conjunto de tres parámetros compartidos (amarillo, naranja y rojo). ¡El número de parámetros caerá de 9 a 3! La nueva arquitectura incluso podría funcionar mejor porque tenemos más datos para entrenar esos pesos específicos. Los pesos después de aplicar la dispersión y los parámetros compartidos se denominan “kernel de convolución”.
| Before Applying Parameter Sharing.png) |
|  After Applying Parameter Sharing.png) |
|Figura 3(a): Antes de compartir parámetros | Figura 3(b): Después de compartir parámetros|
|
|Figura 3(a): Antes de compartir parámetros | Figura 3(b): Después de compartir parámetros|
Las siguientes son algunas ventajas de usar dispersión y parámetros compartidos:
- Uso parámetros compartidos * convergencia más rápida * mejor generalización * no limitado al tamaño de entrada * independencia de kernels $\Rightarrow$ alta paralelización
- Dispersión de conexiones * reduce la cantidad de cómputo
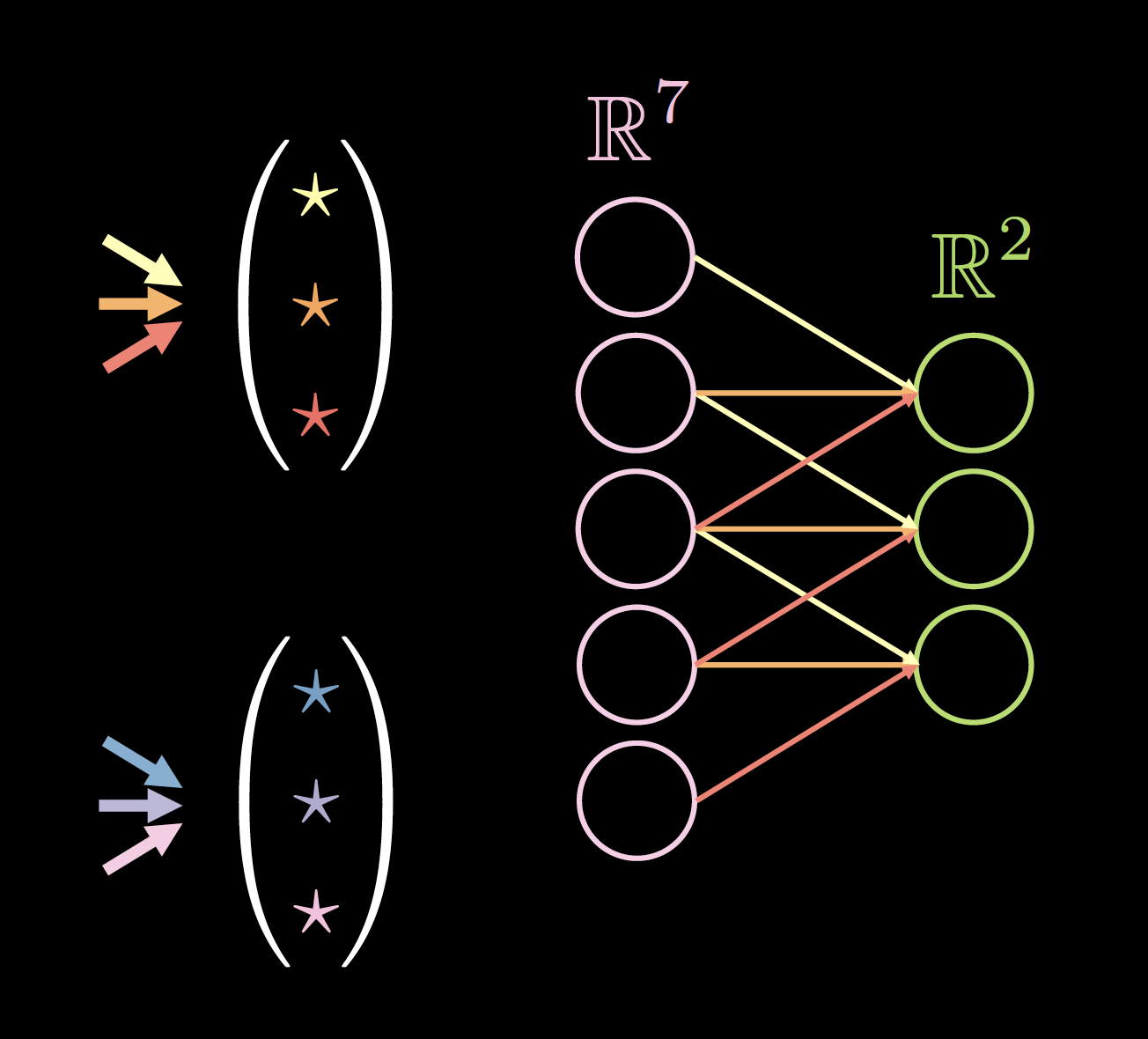
La figura 4 muestra un ejemplo de kernels sobre datos unidimensionales, donde el tamaño del kernel es: 2 (número de kernels) * 7 (ancho de la capa anterior) * 3 (número de conexiones/pesos únicos).
La elección del tamaño del kernel es empírica. La convolución de 3 * 3 parece ser el tamaño mínimo para los datos espaciales. La convolución de tamaño uno se puede usar para obtener una capa final que se puede aplicar a una imagen de entrada más grande. Tamaños de kernel de un número par podrían disminuir la calidad de los datos, por lo que siempre usamos un tamaño de kernel de números impares, generalmente 3 o 5.
| |
| 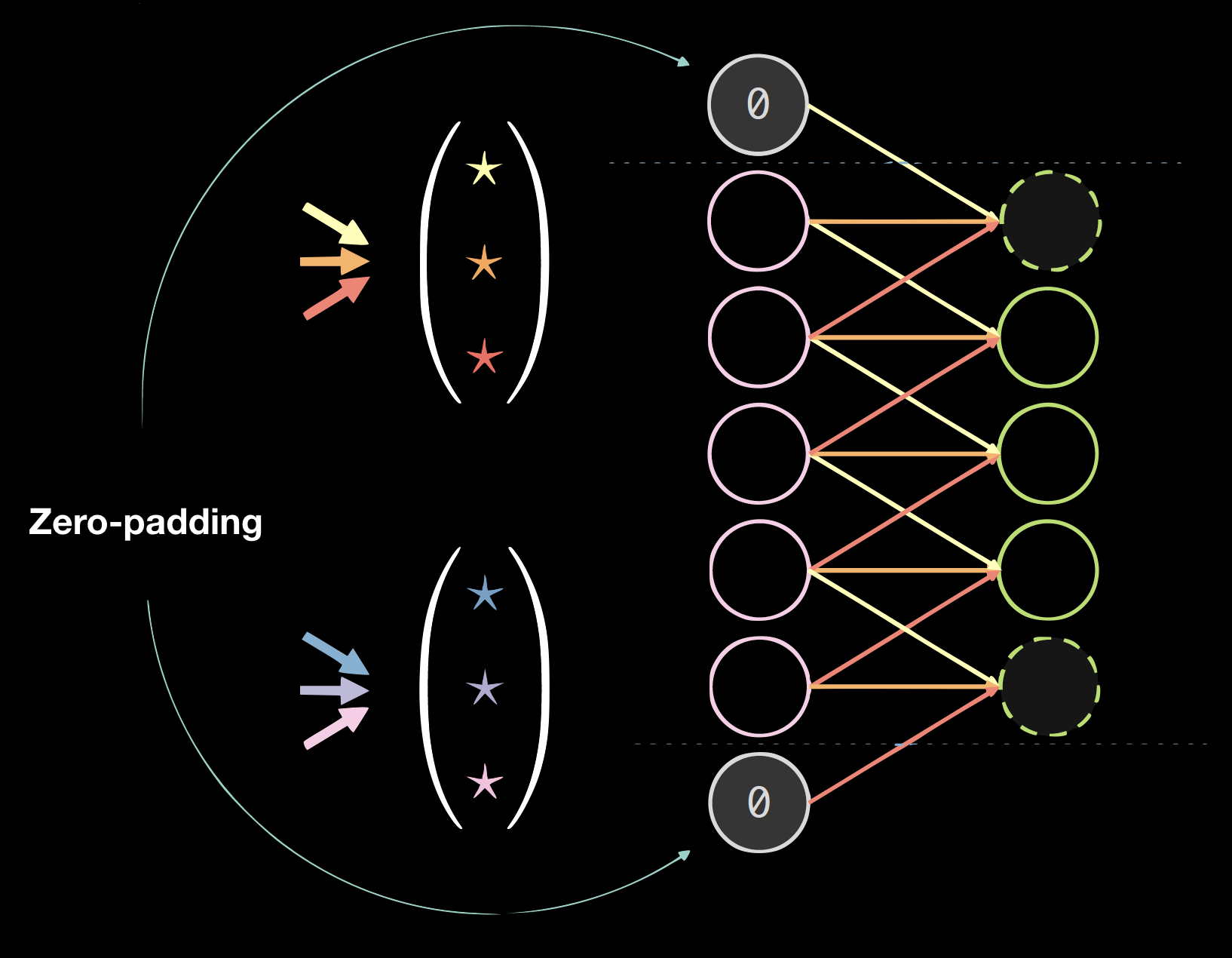 |
|Figura 4(a): Kernels sobre datos unidimensionales | Figura 4(b): Datos con padding de ceros|
|
|Figura 4(a): Kernels sobre datos unidimensionales | Figura 4(b): Datos con padding de ceros|
Padding
Aplicar padding (relleno) generalmente perjudica los resultados finales, pero es conveniente a nivel programación. Solemos usar padding de ceros: tamaño = (tamaño del kernel - 1) / 2.
CNN espacial estándar
Una CNN espacial estándar tiene las siguientes propiedades:
- Múltiples capas * Convolución * No linealidad (ReLU y Leaky) * Pooling * Normalización por lotes (Batch normalization)
- Conexión residual de derivación (residual bypass conection)
Batch normalization y las conexiones residuales de derivación son muy útiles para que la red entrene bien. Pueden perderse partes de una señal si se apilan demasiadas capas, por lo que agregar conexiones de derivación garantizan una ruta para que la información circule de abajo hacia arriba y también una ruta para los gradientes que vienen de arriba hacia abajo.
En la figura 5, mientras que la imagen de entrada contiene principalmente información espacial en dos dimensiones (aparte de la información característica, que es el color de cada pixel), la capa de salida es gruesa. A mitad de camino, existe un equilibrio entre la información espacial y la información característica, y la representación se vuelve más densa. Por lo tanto, a medida que avanzamos en la jerarquía, obtenemos una representación más densa al mismo tiempo que perdemos información espacial.
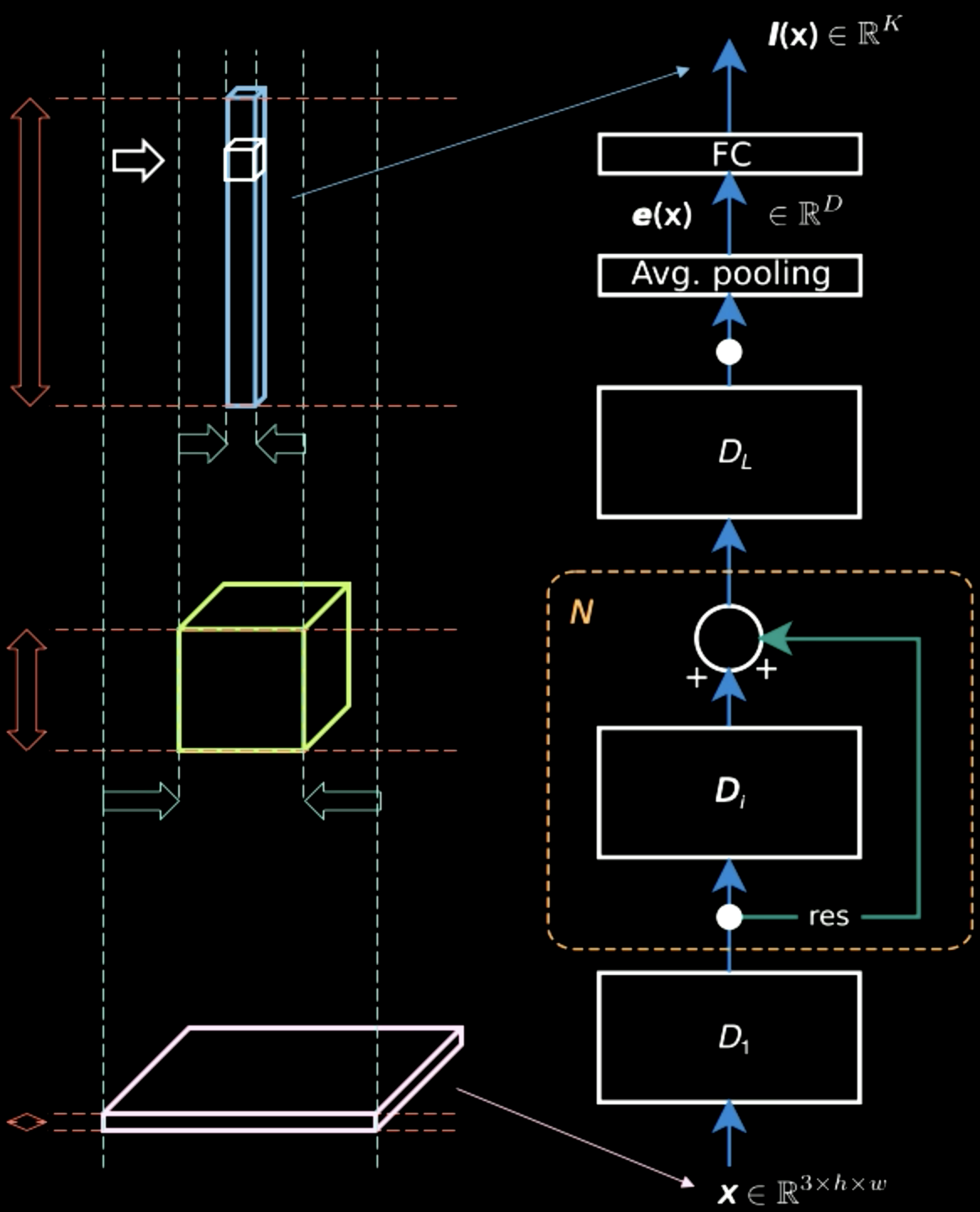
Figura 5: Representaciones de la información a medida que subimos en la jerarquía
Pooling
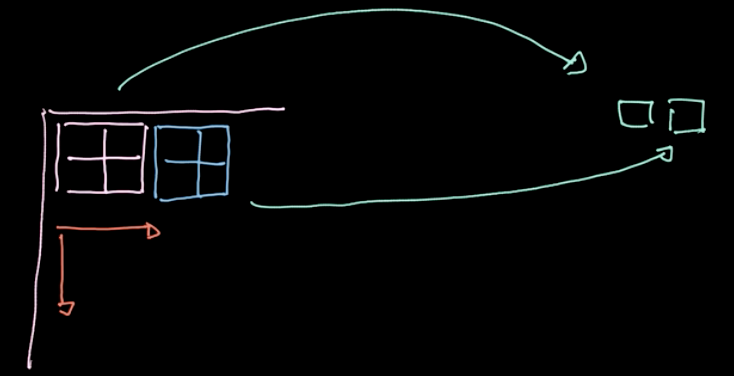
Figura 6: Illustración del *pooling*
Un operador específico, Norma-$L_p$, se aplica a diferentes regiones (ver la figura 6). Tal operador da solo un valor por región (un valor para cuatro pixeles en nuestro ejemplo). Luego iteramos sobre todos los datos, región por región, avanzando en tamaño de zancada. Si comenzamos con datos de $m * n$ con $c$ canales, terminaremos con datos de $\frac{m}{2} * \frac{n}{2}$ aún con $ c $ canales (ver figura 7). La operación de pooling no está parametrizada; sin embargo, podemos elegir diferentes tipos de pooling, como max pooling, pooling promedio, etc. El objetivo principal de la operación de pooling es reducir la cantidad de datos para poder hacer los cálculos en una cantidad de tiempo razonable.
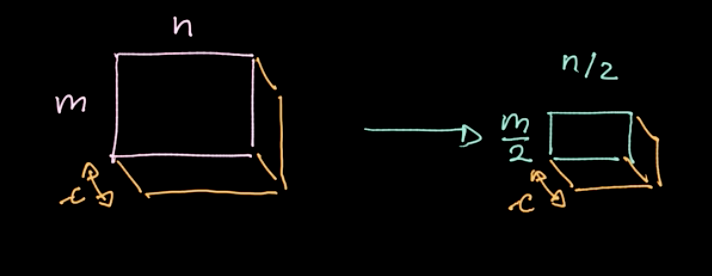
Figura 7: Resultado de aplicar *pooling*
CNN - Jupyter Notebook
El Jupyter Notebook se puede encontrar aquí. Para ejecutarlo, asegúrate de tener instalado el entorno pDL como se especifica en README-ES.md.
En este Notebook, entrenamos un perceptrón multicapa (red FC) y una red neuronal convolucional (CNN) para la tarea de clasificación con el conjunto datos de MNIST. Ten en cuenta que ambas redes tienen el mismo número de parámetros. (ver la figura 8)

Figura 8: Instancias del conjunto de datos MNIST original
Antes de entrenar, normalizamos nuestros datos para que la inicialización de la red coincida con nuestra distribución de datos (¡muy importante!). Además, asegúrate de que las siguientes cinco operaciones/pasos estén presentes en tu algoritmo de entrenamiento:
- Introducción de datos al modelo
- Calcular la función de costo
- Limpiar el caché de gradientes acumulados con
zero_grad() - Calcular los gradientes
- Realizar un paso con el método del optimizador
Primero, entrenamos ambas redes con los datos de MNIST normalizados. La precisión de la red FC resultó ser de $87 \%$ mientras que la precisión de la CNN resultó ser de $95 \%$. Dado el mismo número de parámetros, la CNN logró entrenar muchos más filtros. En la red FC, se entrenan filtros que intentan obtener algunas dependencias entre cosas muy distantes entre sí con cosas que están muy próximas. Son filtros completamente desperdiciados. En cambio, en la red convolucional, todos estos parámetros se concentran en la relación entre pixeles vecinos.
A continuación, realizamos una permutación aleatoria de todos los pixeles en todas las imágenes de nuestro conjunto de datos MNIST. Esto transforma la figura 8 en la figura 9. Luego entrenamos ambas redes en este conjunto de datos modificado.
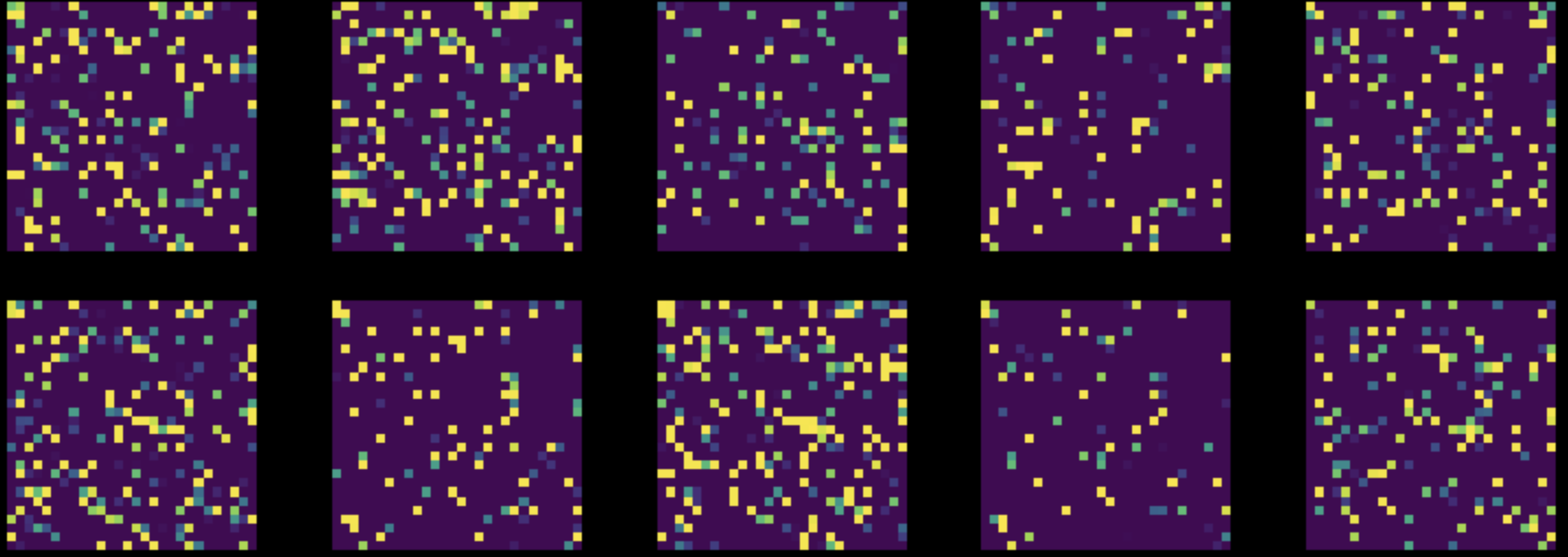
Figura 9: Instancias del conjunto de datos MNIST permutado
El rendimiento de la red FC se mantuvo casi sin cambios ($85 \%$), mientras que la exactitud de la CNN se redujo a $83 \%$. Esto se debe a que, después de una permutación aleatoria, las imágenes ya no tienen las tres propiedades de localidad, estacionariedad y composicionalidad que una CNN puede explotar.
📝 Ashwin Bhola, Nyutian Long, Linfeng Zhang, and Poornima Haridas
LecJackS
11 Feb 2020