Evoluciones de CNNs, Arquitecturas, Detalles y Ventajas de Implementación.

Proto-CNN y evolución hasta las CNN modernas

Redes neuronales proto-convolucionales en pequeños conjuntos de datos

Inspirado por el trabajo de Fukushima en el modelado de la corteza visual, haciendo uso de la jerarquía celular simple/compleja combinada con entrenamiento supervisado y retropropagación, se condujo al desarrollo de la primera CNN en la Universidad de Toronto en los años de 1988-1989 por el profesor Yann LeCun. Los experimentos utilizaron un pequeño conjunto de datos de 320 dígitos ‘escritos’ con el mouse. Se compararon los rendimientos de las siguientes arquitecturas:

1. Una sola capa totalmente conectada (FC: fully connected)
2. Dos capas FC
3. Capas conectadas localmente sin parámetros compartidos
4. Red restringida con pesos compartidos y conexiones locales
5. Red restringida con pesos compartidos y conexiones locales 2 (con más mapeo de características o features)

Las redes más exitosas (red restringida con parámetros compartidos) tenían la mayor capacidad de generalización y forman la base de las CNN modernas. Mientras tanto, el modelo de capa única FC tiende a sobreajustarse (overfitting).

Primeras ConvNets “reales” en los laboratorios Bell

Después de mudarse a Bell Labs, la investigación de LeCunn pasó a utilizar códigos postales escritos a mano del servicio postal de los EE.UU., para entrenar una CNN más grande:

• Capa de entrada de 256 (16$\times$16) valores (pixeles)
• 12 kernels de 5$\times$5 con tamaño de zancada de 2 (avanzaba de a 2 pixeles): la siguiente capa tiene menor resolución
• SIN operación de pooling

Arquitectura de red convolucional con pooling

Al año siguiente, se hicieron algunos cambios: se introdujo una capa de pooling (operación de muestreo) separada. La operación de pooling se realiza promediando los valores de entrada, agregando un sesgo (bias) y pasando a una función no lineal (en este caso la función tangente hiperbólica). El pooling de 2$\times$2 se realizaba con una zancada de 2, reduciendo así las resoluciones a la mitad.

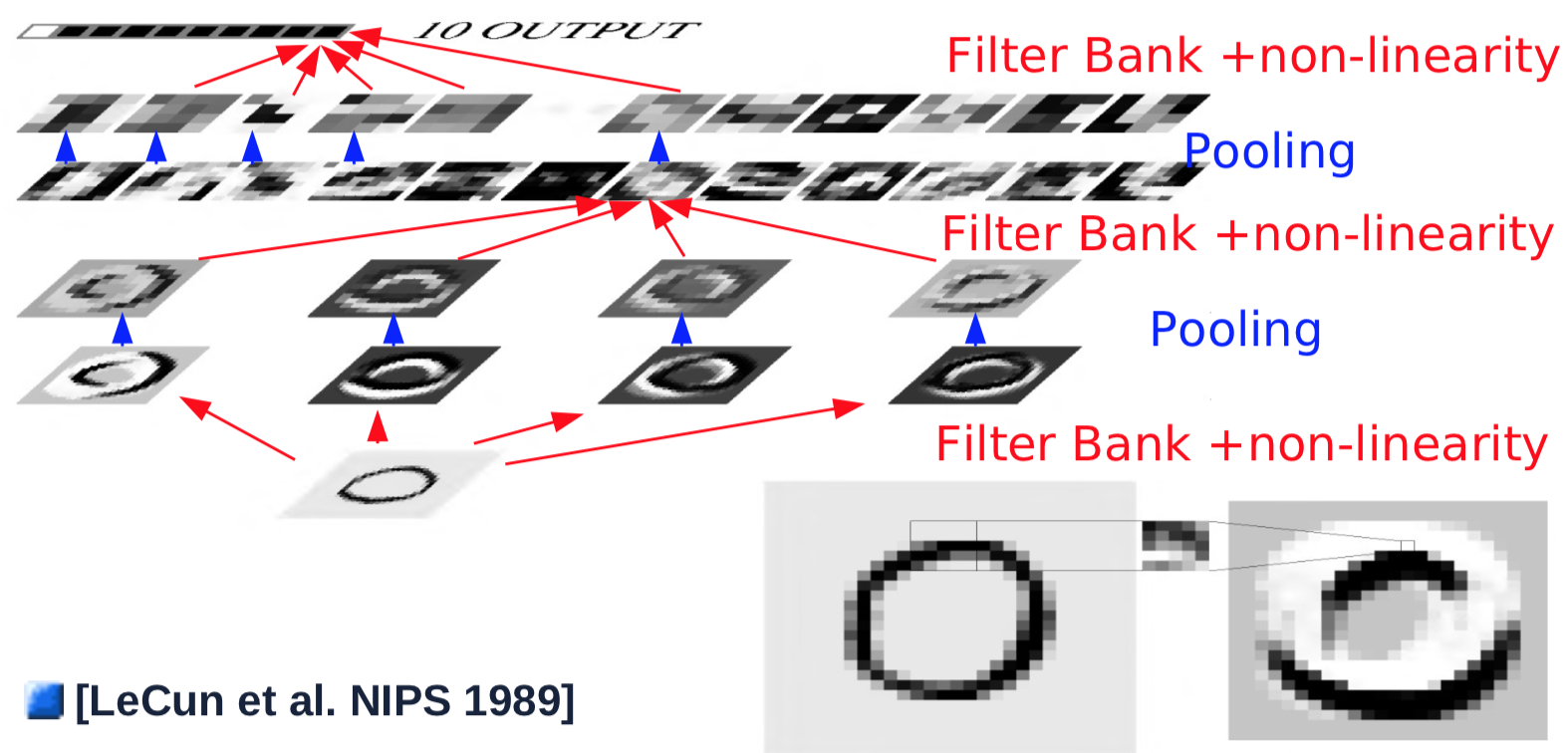
Fig. 1 Arquitectura ConvNet

Un ejemplo de una sola capa convolucional sería el siguiente:

1. Se toma una entrada con tamaño 32$\times$32
2. La capa de convolución pasa sobre la imagen un kernel de 5$\times$5 con zancada 1, con un tamaño mapa de características resultante de 28$\times$28
3. Se pasa el mapa de características por una función no lineal: tamaño resultante 28$\times$28
4. Se pasa a la capa pooling que promedia una ventana de 2$\times$2 con zancada de 2: tamaño resultante 14$\times$14
5. Se repiten los pasos 1 al 4 para cuatro kernels

La primera capa, simples combinaciones de convolución/pooling, generalmente detecta características simples, como deteccion de bordes con orientación. Después de la primera capa de convolución/pooling, el objetivo es detectar combinaciones de características de capas anteriores. Para hacer esto, los pasos 2 al 4 se repiten con múltiples kernels sobre los mapas de características resultantes de la capa anterior y se suman en un nuevo mapa de características:

1. Un nuevo kernel de 5$\times$5 se desliza sobre todos los mapas de características de las capas anteriores y se suman entre sí los resultados. (Nota: en el experimento del Prof. LeCun en 1989, se ignoraban ciertas conexiones por limitaciones computacionales. Las configuraciones modernas generalmente imponen conexiones completas): tamaño de salida 10$\times$10
2. Se pasa la salida de la convolución por una función no lineal: tamaño resultante 10$\times$10
3. Se repiten los pasos 1-2 para 16 kernels
4. Se pasa el resultado a la capa pooling que promedia una ventana de 2$\times$2 con zancada de 2: con tamaño de salida de cada mapa de características de 5$\times$5

Para generar una salida, la última capa de convolución es dirigida, lo que parece a una conexión completa, pero de hecho es convolucional.

1. La capa de convolución final desliza un kernel 5$\times$5 sobre todos los mapas de características, con los resultados sumados: tamaño 1$\times$1
2. Se pasa a través de la función no lineal: tamaño 1$\times$1
3. Se genera una única salida para una categoría
4. Se repiten todos los pasos anteriores para cada una de las diez categorías (en paralelo)

Ve esta animación en el sitio web de Andrej Karpathy, sobre cómo las convoluciones cambian la forma de los mapas de características de la siguiente capa. El artículo completo se puede encontrar aquí.

Equivarianza a los desplazamientos

Fig. 2 Equivarianza a los cambios de posición

Como lo demuestra la animación en las diapositivas (este es otro ejemplo), trasladar la imagen de entrada da como resultado la misma traslación de los mapas de características. Sin embargo, los cambios en los mapas de características se escalan por operaciones de convolución/pooling. Por ejemplo, el pooling de 2$\times$2 con zancada de 2 reducirá el desplazamiento de un pixel en la capa de entrada a un desplazamiento de 0.5 pixeles en los siguientes mapas de características. La resolución espacial se intercambia por un mayor número de tipos de características, es decir, haciendo que la representación sea más abstracta y menos sensible a los cambios de posición y distorsiones.

Desglose general de la arquitectura

La arquitectura genérica de las CNN se puede dividir en varios arquetipos de capa básica:

• Normalización
  • Ajuste de blanqueamiento (opcional)
  • Métodos sustractivos, por ejemplo: sustracción del promedio, filtrado pasa altas
  • Divisivo: normalización de contraste local, normalización de varianza

• Bancos de Filtrado
  • Aumenta la dimensionalidad
  • Proyección sobre bases completas
  • Detecciones de bordes

• No linealidades
  • Aumento de dispersión
  • Típicamente Unidad Lineal Rectificada (ReLU): $\text{ReLU}(x) = \max(x, 0)$

• Pooling
  • Muestreo sobre un mapa de características

  • Max Pooling: $\text{MAX}= \text{Max}_i(X_i)$

  • Pooling de norma-LP: \(\text{L}p= \left(\sum_{i=1}^n \|X_i\|^p \right)^{\frac{1}{p}}\)

  • Pooling de probabilidad-Logarítmica: $\text{Prob}= \frac{1}{b} \left(\sum_{i=1}^n e^{b X_i} \right)$

LeNet5 y reconocimiento de dígitos

Implementación de LeNet5 en PyTorch

LeNet5 está formado por las siguientes capas (siendo 1 la capa superior)

1. Log-softmax
2. Capa Fully Connected de dimensiones 500$\times$10
3. ReLu
4. Capa Fully Connected de dimensiones (4$\times$4$\times$50)$\times$500
5. Max Pooling de dimensiones 2$\times$2, zancada de 2
6. ReLu
7. Convolución con 20 canales de salida, kernel de 5$\times$5, zancada de 1
8. Max Pooling de dimensiones 2$\times$2, zancada de 2
9. ReLu
10. Convolución con 20 canales de salida, kernel de 5$\times$5, zancada de 1

La entrada es una imagen en escala de grises de 32$\times$32 (1 canal de entrada).

LeNet5 se puede implementar en PyTorch con el siguiente código:

class LeNet5(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.conv2 = nn.Conv2d(20, 20, 5, 1)
        self.fc1 = nn.Linear(4*4*50, 500)
        self.fc2 = nn.Linear(500, 10)

    def forward(self, x):
    x = F.relu(self.conv1(x))
    x = F.max_pool2d(x, 2, 2)
    x = F.relu(self.conv2(x))
    x = F.max_pool2d(x, 2, 2)
    x = x.view(-1, 4*4*50)
    x = F.relu(self.fc1)
    x = self.fc2(x)
    return F.logsoftmax(x, dim=1)

Aunque fc1 y fc2 son capas completamente conectadas (FC), pueden considerarse capas convolucionales cuyos kernels cubren toda la entrada. Las capas completamente conectadas se utilizan con fines de eficiencia.

El mismo código puede expresarse usando nn.Sequential, pero está desactualizado.

Ventajas de las CNN

En una red totalmente convolucional, no es necesario especificar el tamaño de la entrada. Sin embargo, cambiar el tamaño de la entrada también cambia el tamaño de la salida.

Considera un sistema de reconocimiento de escritura cursiva a mano. No es necesario dividir la imagen de entrada en segmentos. Podemos aplicar la CNN sobre toda la imagen: los kernels cubrirán todas las ubicaciones de la imagen completa y registrarán la misma salida independientemente de dónde se encuentre el patrón. Aplicar la CNN sobre una imagen completa es mucho más barato que aplicarla en varias ubicaciones por separado. No se requiere segmentación previa, lo cual es un alivio porque la tarea de segmentar una imagen es similar a la de reconocer una imagen.

Ejemplo: MNIST

LeNet5 está entrenada con imágenes de MNIST de tamaño 32$\times$32 para la clasificación de dígitos individuales en el centro de la imagen. Se utilizó una técnica de aumento de datos de entrenamiento al mover el dígito, cambiar el tamaño del dígito e insertar otros dígitos a un lado. También se entrenó con una categoría 11 que representaba a niguna de las anteriores. Las imágenes etiquetadas con esta categoría se generaron ya sea produciendo imágenes completamente en blanco o colocando dígitos a un lado pero no en el centro.

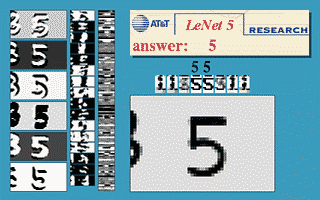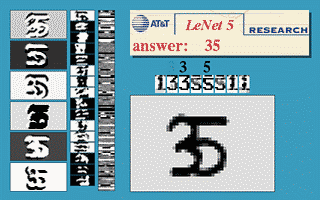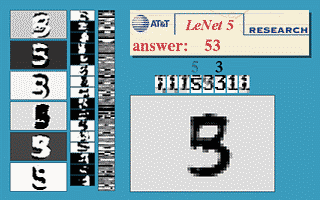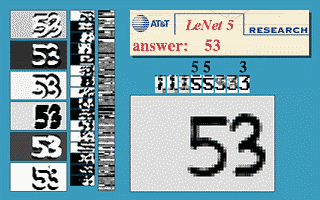
Fig. 3 Ventana deslizante de una ConvNet

La imagen de arriba demuestra que una red LeNet5 entrenada con imáges de 32$\times$32 se puede aplicar en una imagen de entrada de 32$\times$64 px para reconocer el dígito en múltiples ubicaciones.

Problema de unión de características

¿Cuál es el problema de unión de características?

Los neurocientíficos visuales y los profesionales en el área de visión por computadora tienen el problema de definir el objeto como un objeto. Un objeto es una colección de características, pero ¿cómo vincular todas las características para formar este objeto?

¿Cómo solucionarlo?

Podemos resolver este problema de unión de características usando una CNN muy simple: solo dos capas de convoluciones con pooling más otras dos capas completamente conectadas sin ningún mecanismo específico para ello, dado que tenemos suficientes no linealidades y datos para entrenar nuestra CNN.

Fig. 4 ConvNet interpretando la unión de características

La animación anterior muestra la capacidad de las CNN para reconocer diferentes dígitos al mover un solo trazo, lo que demuestra su capacidad para abordar problemas de unión de características, es decir, reconocer características de forma jerárquica y composicional.

Ejemplo: longitud de entrada dinámica

Podemos construir una CNN con dos capas de convolución con zancada de uno y dos capas de pooling con zancada de dos, de modo que la zancada general sea cuatro. Por lo tanto, si queremos obtener una nueva salida, debemos desplazar nuestra ventana de entrada en cuatro. Para ser más explícitos, podemos ver la siguiente figura (unidades verdes). Primero, tenemos una entrada de tamaño diez y realizamos una convolución de tamaño tres para obtener ocho unidades. Después de eso, realizamos un pooling de tamaño dos para obtener cuatro unidades. Del mismo modo, repetimos nuevamente la convolución y el pooling y, finalmente, obtenemos una salida.

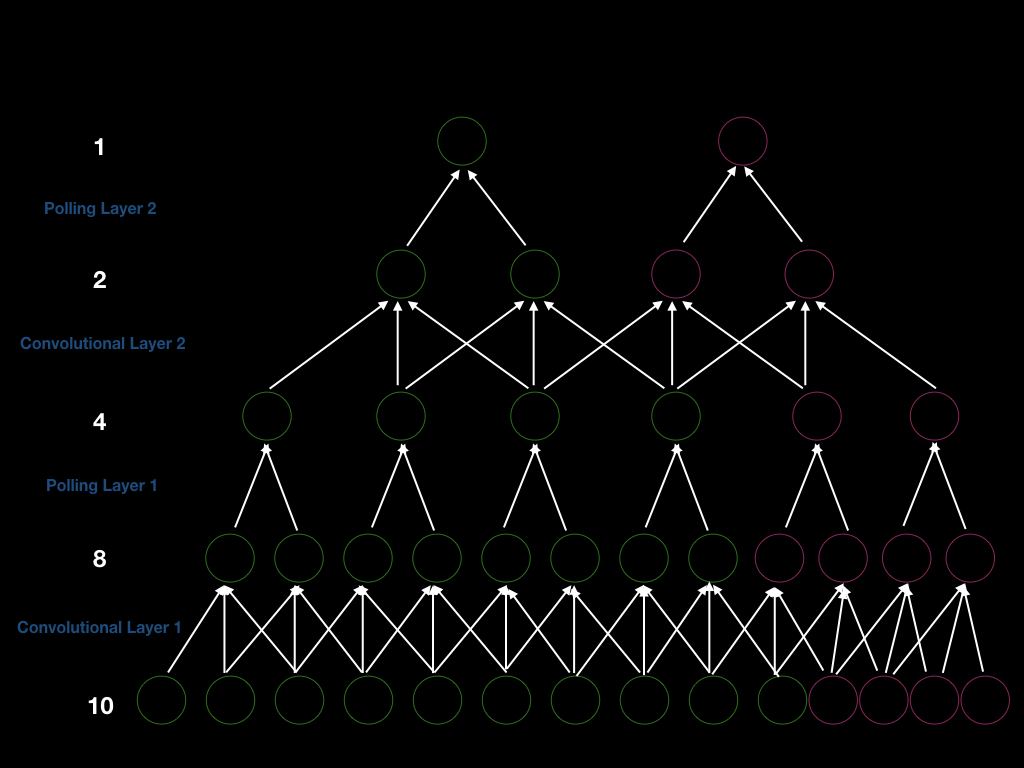
Fig. 5 Arquitectura ConvNet sobre unión de tamaño de entrada variante

Supongamos que agregamos cuatro unidades en la capa de entrada (unidades rosa en la imagen de arriba), para que podamos obtener cuatro unidades más después de la primera capa de convolución, dos unidades más después de la primera capa de pooling, dos unidades más después de la segunda capa de convolución capa y una salida más. Por lo tanto, el tamaño de la ventana para generar una nueva salida es cuatro (zancadas de 2 $\times$2). Además, esto es una demostración del hecho de que si aumentamos el tamaño de la entrada, aumentaremos el tamaño de cada capa, demostrando la capacidad de las CNN de manejar entradas de longitud dinámica.

¿En qué son buenas las CNN?

Las CNNs son buenas para señales que llegan en forma de arreglos multidimensionales. Estas señales tienen tres propiedades principales.

1. Localidad: La primera es que existe una fuerte correlación local entre los valores. Si tomamos dos pixeles cercanos de una imagen natural, es muy probable que esos pixeles tengan el mismo color. A medida que dos pixeles se separen más, la similitud entre ellos disminuirá. Las correlaciones locales pueden ayudarnos a detectar características locales, que es lo que están haciendo las CNN. Si alimentamos la CNN con pixeles permutados, no funcionará bien al reconocer las imágenes de entrada, mientras que una FC no se verá afectada por ello. La correlación local justifica las conexiones locales.
2. Estacionariedad: La segunda propiedad es que las características son esenciales y pueden aparecer en cualquier lugar de la imagen, lo que justifica los parámetros compartidos y el pooling. Además, las señales estadísticas se distribuyen uniformemente, lo que significa que debemos repetir la detección de características para cada ubicación en la imagen de entrada.
3. Composicionalidad: La tercera propiedad es que las imágenes naturales son composicionales, lo que significa que las características componen una imagen de manera jerárquica. Esto justifica el uso de múltiples capas de neuronas, que también se corresponde estrechamente con la investigación de Hubel y Wiesel sobre células simples y complejas.

Además, las personas hacen un buen uso de las CNN en videos, imágenes, textos y para el reconocimiento de voz.