Visualización de transformación de párametros vía red neuronal y conceptos fundamentales de convolución

Visualización de redes neuronales

En esta sección visualizaremos cómo funciona una red neuronal por dentro.

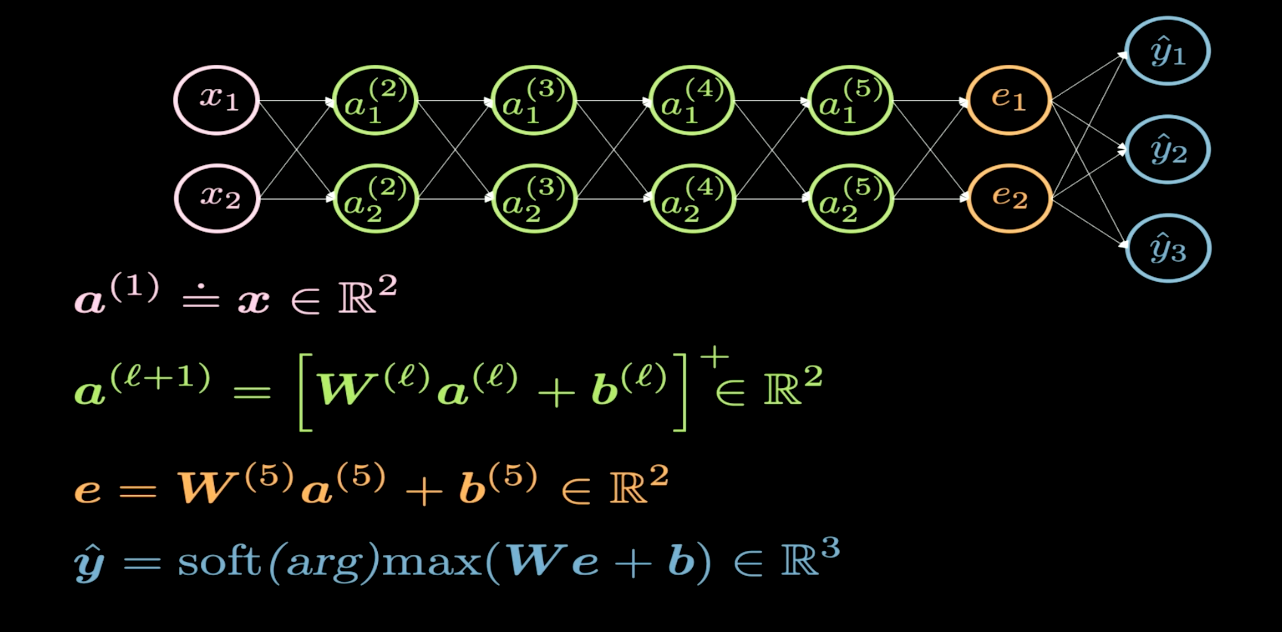
Fig. 1 Estructura de una red

En la figura 1, podemos observar la estructura de la red neuronal que quisiéramos visualizar. Convencionalmente, al dibujar una red, la entrada es colocada en la parte inferior o a la izquierda del diagrama, y la salida, en la parte superior o a la derecha. En la figura 1, las neuronas rosadas representan la entrada, y las azules, la salida. En esta red, tenemos cuatro capas ocultas (en verde); así que tenemos seis capas en total (4 capas ocultas + 1 capa de entrada + 1 capa de salida). Esta red tiene dos neuronas por cada capa oculta; por ende, la dimensión de la matriz de pesos ($W$) en cada capa es $2x2$. Esto es debido a que, en este caso, queremos transformar el plano de entrada (2D) a otro plano (2D) que podemos visualizar.

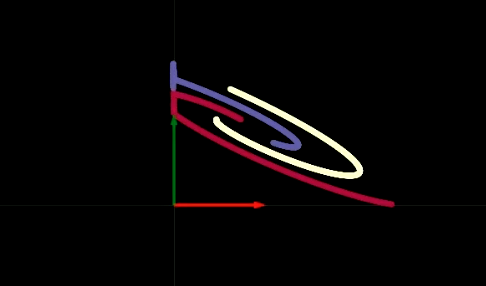
Fig. 2 Visualización del espacio siendo doblado por la red

La transformación que ocurre en cada capa de la red es análoga a doblar nuestro plano en algunas regiones específicas como se muestra en la figura 2. Este doblez es muy abrupto dado que todas las transformaciones ocurren la capa de dos dimensiones. En este experimento, encontramos que si solo tenemos dos neuronas en cada capa oculta, la optimización toma más tiempo. La optimización sería más fácil si tuviéramos más neuronas en las capas ocultas. Esta discusión nos lleva a una pregunta importante: ¿por qué es más difícil entrenar una red con menos neuronas en las capas ocultas? Deberías meditar en la respuesta; regresaremos más tarde a ella después de la visualización de $\texttt{ReLU}$.

(a)	(b)

Al viajar por la red una capa oculta a la vez, observamos que cada una realiza una transformación afín seguida de aplicar la operación no lineal ReLU, la cual elimina los valores negativos. En las figuras 3(a) y 3(b), podemos ver la visualización del operador ReLU. Este operados nos ayuda a realizar transformaciones no lineales. Después de múltiples pasos que realizan una transformación afín y operación no lineal, obtenemos datos que se pueden separar linealmente como se aprecia en la figura 4.

Fig. 4 Visualización de los datos de salida

Este ejercicio nos provee intuición de por qué la red con dos neuronas en cada capa es más difícil de entrenar. Nuestra red de seis capas tiene un sesgo (bias) en cada capa oculta. Por consiguiente, si uno de estos valores desplaza puntos fuera del cuadrante superior derecho, los puntos desplazados serían eliminados con ReLU (al ser negativos). Después de esto, sin importar cómo las capas subsecuentes transformen los datos, los valores seguirán siendo cero. Podemos agilizar el entrenamiento de la red al hacerla “más gruesa” (es decir, agregando más neuronas en las capas ocultas o agregando más capas ocultas o una combinación de ambos métodos). A lo largo de este curso, exploraremos cómo determinar la mejor arqutectura de la red para un problema dado.

Transformación de parámetros

La transformación general de parámetros se refiere a que nuestro vector de parámetros $w$ es la salida de una función. Con esta transformación, podemos mapear el espacio de parámetros original a algún otro espacio. En la figura 5, $w$ es, de hecho, la salida de $H$ con el parámetro $u$. $G(x,w)$ es una red y $C(y,\bar y)$ es una función de costo. La función de propagación hacia atrás también es adecuada como sigue:

Estas fórmulas se aplican en forma matricial. Presta atención a que las dimensiones de los términos deben de ser consistentes. La dimensión de $u$, $w$, $\frac{\partial H}{\partial u}^\top$, $\frac{\partial C}{\partial w}^\top$ son $[N_u \times 1]$, $[N_w \times 1]$, $[N_u \times N_w]$, $[N_w \times 1]$, respectivamente. Por consiguiente, la dimensión de la propagación hacia atrás es consistente.

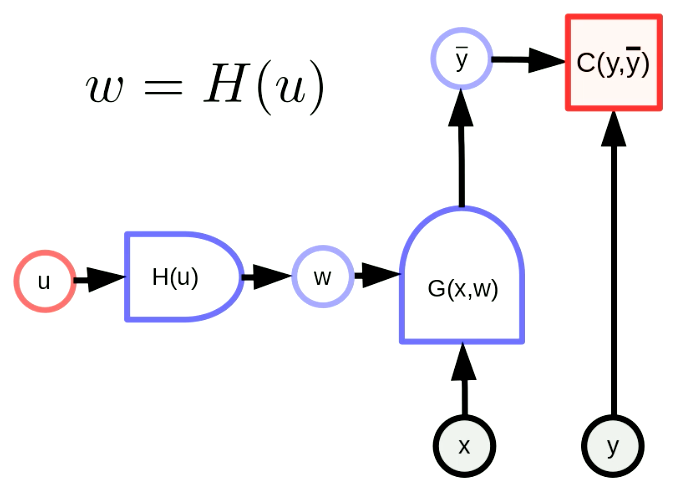
Fig. 5 Forma general de transformación de parámetros

Una transformación de parámetros simple: la reutilización de parámetros

La transformación mediante la reutilización de parámetros (weight sharing) significa que $H(u)$ únicamente replica un componente de $u$ en componentes múltiples de $w$. $H(u)$ es como una rama en forma de Y que copia $u_1$ a $w_1$, $w_2$. Esto se puede expresar de la siguiente manera:

Obligamos a los parámetros compartidos a ser iguales para que el gradiente con respecto a los parámetros compartidos sea sumado en la propagación hacia atrás. Por ejemplo, el gradiente de la función de costo $C(y, \bar y)$ con respecto a $u_1$ es la suma del gradiente de la función de costo $C(y, \bar y)$ con respecto a $w_1$ más el gradiente de la función de costo $C(y, \bar y)$ con respecto a $w_2$.

Hiperredes

Una “hiperred” es una red en la que los pesos de una red son la salida de otra red. La figura 6 muestra el grafo computacional de una “hiperred”. En esta, la función $H$ es una red con un vector de parámetros $u$ y entrada $x$. Esto resulta en que los pesos de $G(x,w)$ son configurados dinámicamente por la red $H(x,u)$. A pesar de que esto no es una idea nueva, sigue siendo una implementación muy poderosa.

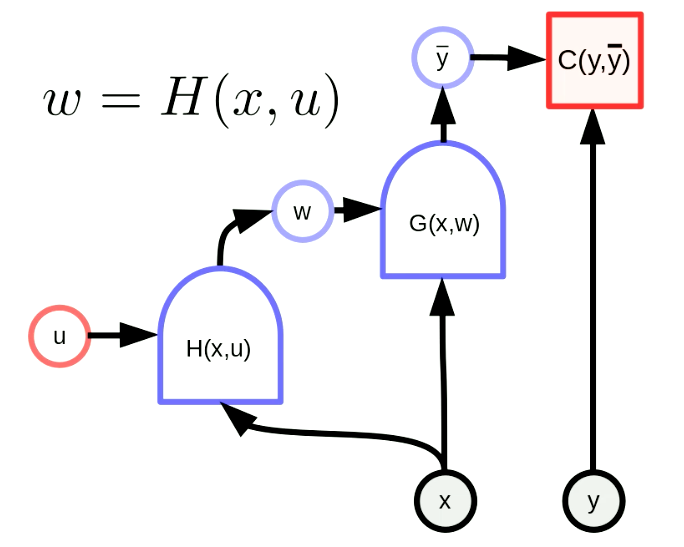
Fig. 6 "hiperred"

Detección de patrones en datos secuenciales

La transformación mediante la reutilización de parámetros (weight sharing) puede ser utilizada para detectar patrones. Esto se refiere a la localización de patrones repetidos en datos secuenciales como palabras clave en voz o texto. Una forma de lograr esto, como se demuestra en la figura 7, es deslizar una ventana en los datos, la cual desplaza la función con parámetros reutilizados para detectar un patrón específico (es decir, un sonido en específico en una señal de voz), y la salida (es decir, una calificación) va hacia una función que busca el valor máximo.

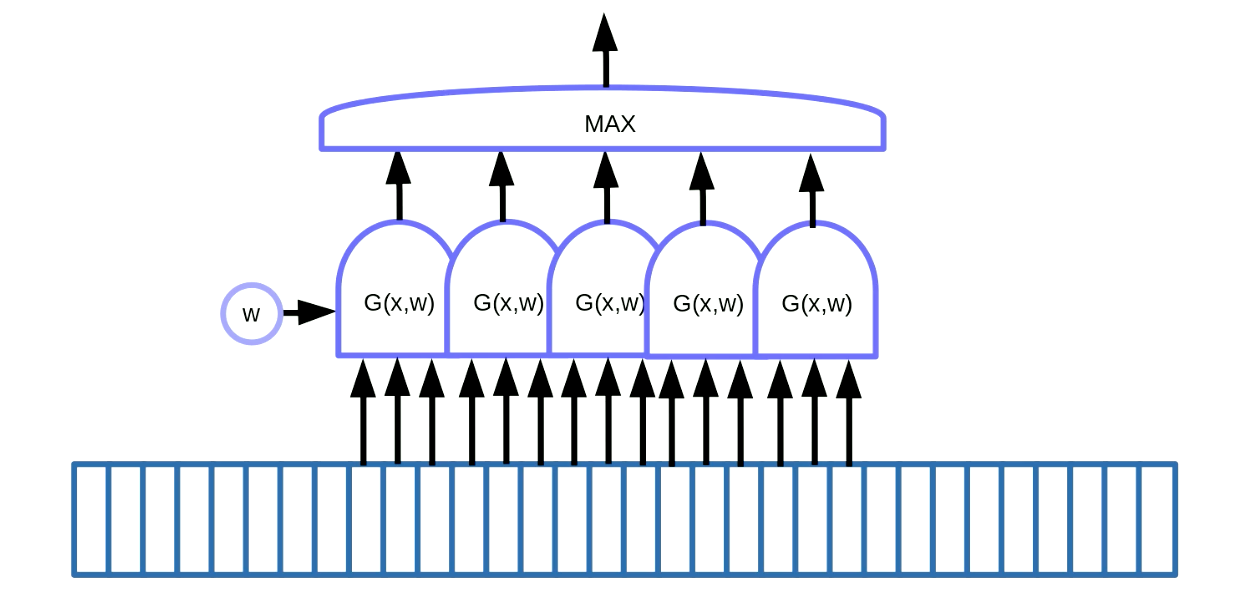
Fig. 7 Detección de patrones en datos secuenciales

En este ejemplo tenemos cinco de estas funciones. Como resultado de esta solución, sumamos cinco gradientes y realizamos una propagación hacia atrás del error para actualizar el parámetro $w$. Al implementar esto en PyTorch, queremos evitar la acumulación implícita de estos gradientes, así que necesitamos usar zero_grad() para inicializar el gradiente.

### Detección de patrones en imágenes

<!– The other useful application is motif detection in images. We usually swipe our “templates” over images to detect the shapes independent of position and distortion of the shapes. A simple example is to distinguish between “C” and “D”, as Figure 8 shows. The difference between “C” and “D” is that “C” has two endpoints and “D” has two corners. So we can design “endpoint templates” and “corner templates”. If the shape is similar to the “templates”, it will have thresholded outputs. Then we can distinguish letters from these outputs by summing them up. In Figure 8, the network detects two endpoints and zero corners, so it activates “C”.

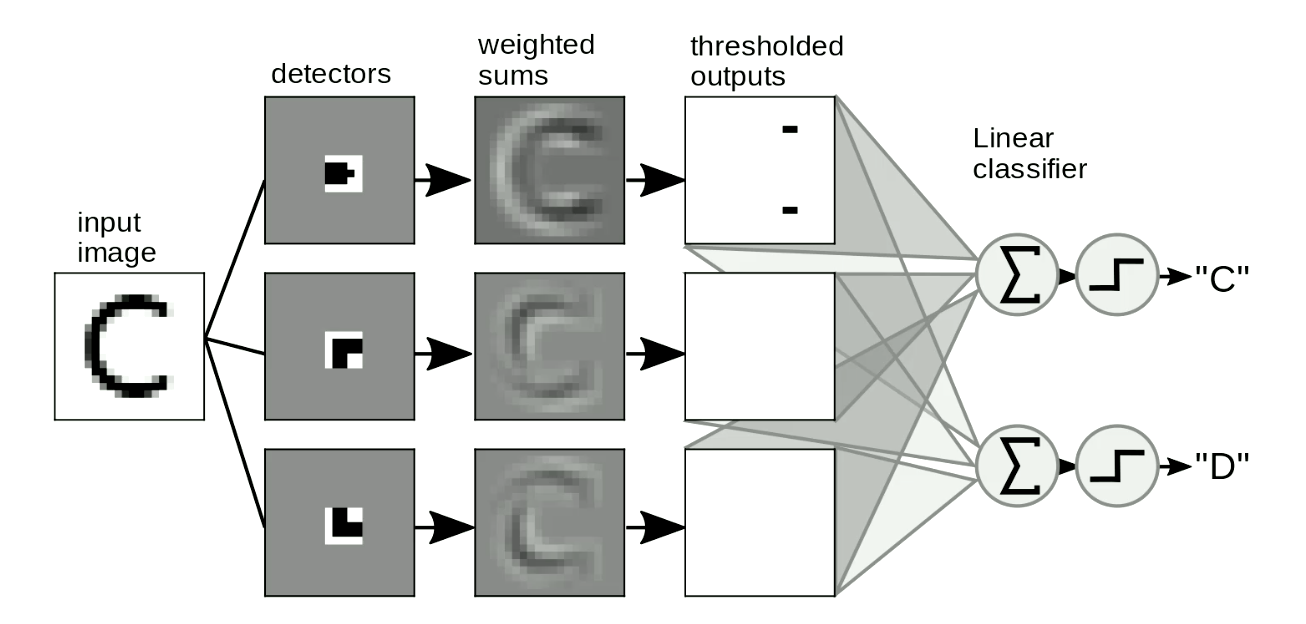
Fig. 8 Motif Detection for Images

It is also important that our “template matching” should be shift-invariant - when we shift the input, the output (i.e. the letter detected) shouldn’t change. This can be solved with weight sharing transformation. As Figure 9 shows, when we change the location of “D”, we can still detect the corner motifs even though they are shifted. When we sum up the motifs, it will activate the “D” detection.

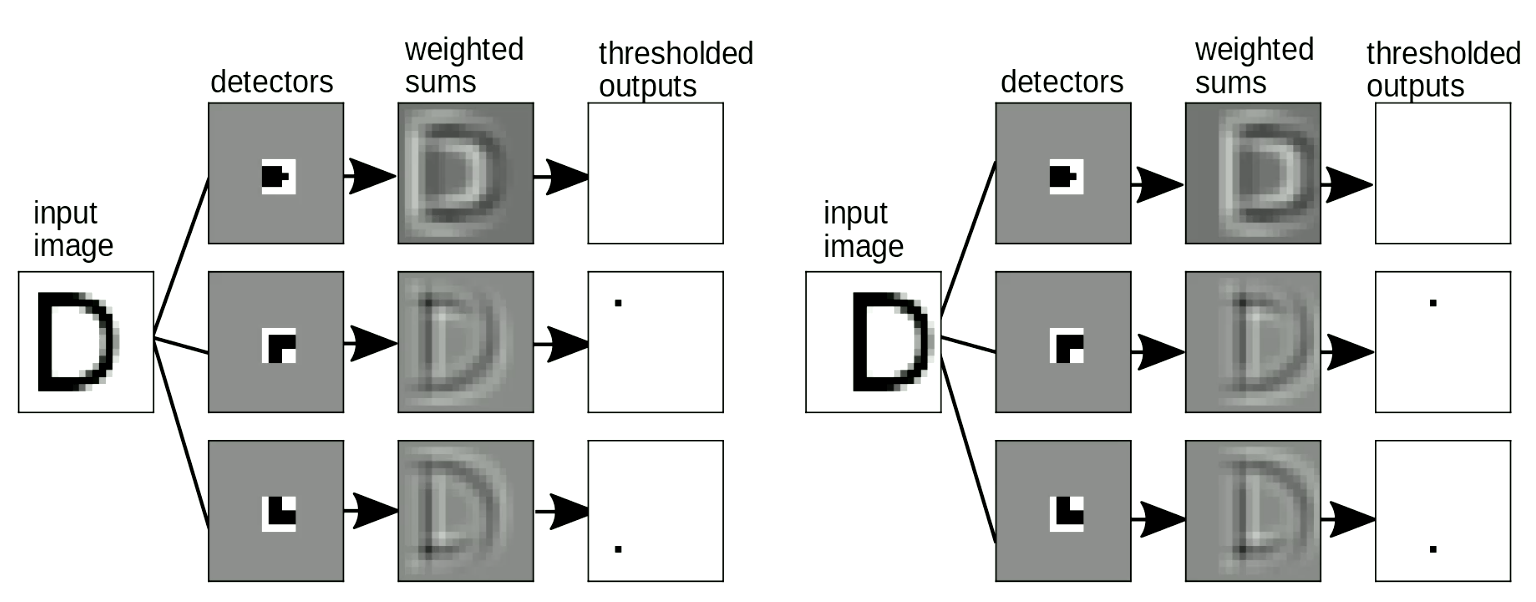
Fig. 9 Shift Invariance

This hand-crafted method of using local detectors and summation to for digit-recognition was used for many years. But it presents us with the following problem: How can we design these “templates” automatically? Can we use neural networks to learn these “templates”? Next, We will introduce the concept of convolutions , that is, the operation we use to match images with “templates”. –>

La otra apliación útil es en la detección de patrones en imágenes. Usualmente, deslizamos nuestras “plantillas” sobre las imágenes para detectar formas independientemente de la posición y distorción de las formas. Un ejemplo simple es distinguir entre las letras “C” y “D” como se muestra en la figura 8. La diferencia entre las letras “C” y “D” es que la “C” tiene dos extremos, mientras que la letra “D” tiene dos esquinas. Así que podemos diseñar “plantillas de extremos” y “plantillas de esquinas”. Si la forma es similar a estas “plantillas”, tendrá salidas umbralizadas. Entonces podemos distinguir letras a partir de estas salidas al sumarlas. En la figura 8, la red detecta dos extremos y ninguna esquina; así que activa la respuesta “C”.

Fig. 8 Detección de patrones en imágenes

También es importante que nuestro método con “plantillas” sea invariante al desplazamiento (al desplazar la entrada, la salida–la letra detectada–no debería cambiar). Esto se puede lograr con la transformación de la reutilización de parámetros (weight sharing). Como se aprecia en la figura 9, al cambiar la ubicación de “D”, aún podemos detectar los patrones de esquinas pese a que fueron desplazadas. Al sumar los patrones, se activará la detección de “D”.

Fig. 9 Invariancia al desplazamiento

Este método manual de utilización de detectores locales y sumas para detección de dígitos se utilizó por muchos años. Sin embargo, este presenta un problema: ¿cómo podemos diseñar estas “plantillas” automáticamente? ¿Es posible utilizar redes neuronales para aprender estas “plantillas”? A continuación, presentaremos el concepto de convoluciones, es decir, la operación que utilizamos para operar las “plantillas” en imágenes.

Convolución discreta

Convolución

La definición matématica precisa de la convolución en el caso unidimensional entre la entrada $x$ y $w$ es:

En palantas, la $i$-ésima salida se calcula como el producto punto entre el reverso de $w$ y una ventana del mismo tamaño en $x$. Para calcular la salida completa, comienza con la ventana al inicio, desplaza esta ventana un lugar cada vez y repite hasta haber terminado con $x$.

Correlación cruzada

En la práctica, la convención de los sistemas de aprendizaje profundo como PyTorch es ligeramente diferente. La convolución en PyTorch está implementada sin revertir $w$:

Los matemáticos denotan a esta fórmula como “correlación cruzada”. En nuestro contexto, esta diferencia es únicamente en la convención. En la práctica, los términos correlación cruzada y convolución son intercambiables si uno lee los pesos guardados en la memoria hacia delante o hacia atrás.

Ser conscientes de esta diferencia es importante, por ejemplo, si uno quiere hacer uso de ciertas propiedades de la correlación cruzada o la convolución de textos matemáticos.

Convolución en más dimensiones

Para entradas bidimensiones como son las imágenes, usamos la versión bidimensional de la convolución:

Esta definición puede extenderse fácilmente a tres o cuatro dimensiones. Aquí, $w$ es llamado kernel de convolución.

Variantes para el operador convolucional en DCNN

1. Zancadas (Striding): en lugar de desplazar la ventana en $x$ una entrada a la vez, se puede realizar con un paso más grande (por ejemplo, dos o tres entradas a la vez). Ejemplo: Supón que la entrada $x$ es unidimensional y tiene un tamaño de 100 y que $w$ tiene un tamaño de cinco. El tamaño de la salida con una zancada (stride) de uno o dos se muestra en la siguiente tabla:

1. Relleno (Padding): Con frecuencia, al diseñar arquitecturas de redes neuronales profundas, queremos que la salida de la convolución sea del mismo tamaño que los datos de entrada. Esto puede lograrse rellenando los extremos de la entrada con un número de (comúnmente) ceros. Este relleno se realiza principalmente por comodidad. A veces puede tener un impacto negativo en el desempeño y resultar en extraños efectos en los bordes. Habiendo dicho esto, al utilizar una no linealidad como ReLU, rellenar con ceros es razonable.

Redes neuronales convolucionales profundas (DCNN)

Como se describió previamente, las redes neuronales profundas están típicamente organizadas en secciones que alternan operadores lineales y capas con operaciones no-lineales que operan punto a punto. En las redes neuronales convolucionales, el operador lineal será el operador de convolución descrito anteriormente. Adicionalmente, existe un tercer tipo opcional de capa denominado capa de muestreo (pooling).

La razón detrás de apilar varias de estas capas es debido a que queremos construir una representación jerárquica de los datos. Las CNN no están limitadas al procesamiento de imágenes. También se han aplicado con éxito a voz y lenguaje. Técnicamente, pueden aplicarse a cualquier tipo de datos que estén organizados en arreglos (de cualquier dimensión) que cumplan con ciertas propiedades.

¿Por qué querríamos capturar la representación jerárquica del mundo? Debido a que el mundo en el que vivimos es composicional. Se ha hecho alusión a este punto en la secciones anteriores. Dicha naturaleza jerárquica puede observarse del hecho de que grupos de pixeles locales se ensamblan para formar patrones simples, tales como bordes orientados. Estos bordes a su vez se ensamblan para formar características locales tales como esquinas, juniones en forma de “T”, etc. Estos bordes se ensamblan para formar patrones que son incluso más abstractos. Podemos continuar construyendo estas representaciones jerárquicas hasta llegar a los objectos que observamos en el mundo real.

Fig. 10. Visualización de características de una red convolucional entrenada en ImageNet [Zeiler & Fergus 2013]

Esta naturaleza jerárquica y composicional que observamos en el mundo natural es, por lo tanto, no solo resultado de nuestra percepción visual, sino también verdadera al nivel físico. En el nivel más bajo de la descripción, tenemos partículas elementales que al ensamblarse forman átomos, estos últimos en conjunto forman moléculas, que a su vez forman materiales y partes de objetos hasta que, al final, forman objectos completos en el mundo real.

La naturaleza composicional del mundo podría ser la respuesta a la pregunta retórica de Einstein de cómo los humanos entienden el mundo en que viven.

La cuestión más incomprensible del universo es que es comprensible

El hecho de que los humanos entiendan el mundo gracias a esta naturaleza composicional sigue pareciendo una conspiración para Yann. Sin embargo, se puede argumentar que sin composicionalidad, tomaría incluso más magia para los humanos comprender el mundo en el que viven. Parafraseando al gran matemático Stuart Geman:

El mundo es composicional o Dios existe.

Inspiración de la biología

¿Por qué el aprendizaje profundo debe estar arraigado en la idea de que nuestro mundo es comprensible y tiene una naturaleza composicional? Estudios conducidos por Simon Thorpe ayudaron a motivar esta pregunta. Él demostró que la manera en que reconocemos objetos cotidianos es muy rápida. Sus experimentos consistieron en mostrar rápidamente un conjunto de imágenes cada 100 ms y enseguida preguntar a sus usuarios que identificaran estas imagenes, quienes fueron capaces de hacerlo. Esto demostró que solo le toma 100 ms a los humanos detectar objetos. Adicionalmente, considera el siguiente diagrama, que ilustra las distintas partes del cerebro indicando el tiempo que toma para que las neuronas propaguen información de un área a otra:

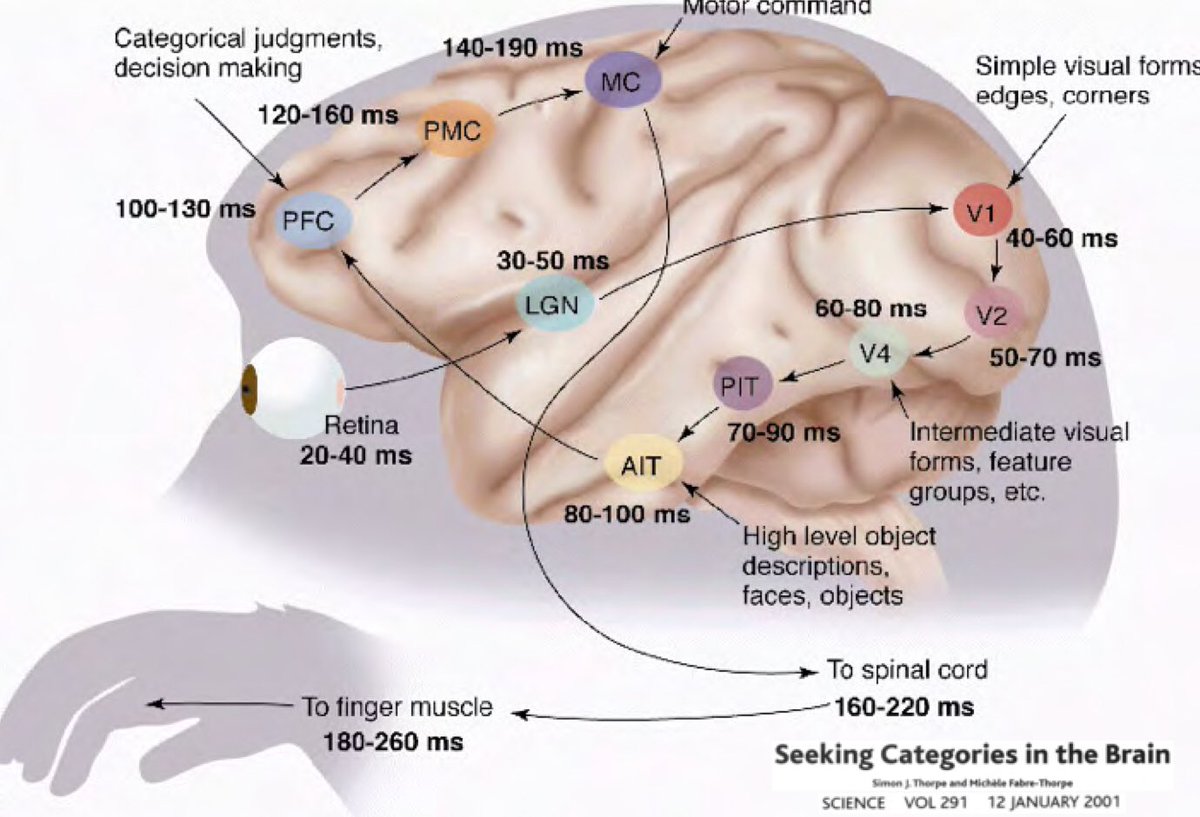
Las señales pasan de la retina al núcleo geniculado lateral (LGN, por sus siglas en inglés), que ayuda con la mejora del contraste, el manejo de compuertas, etc. Luego proceden al córtex visual primario V1, V2, V4, seguido del córtex inferotemporal (PIT, por sus siglas en inglés), el cual es la parte del cerebro donde las categorías están definidas. Observaciones de cirugías abiertas cerebrales han mostrado que si se le muestra a un humano una película, las neuronas en el PIT se activarán únicamente cuando detecten ciertas imágenes–como Jennifer Aniston o la abuela de alguna persona–y de ninguna otra forma. Las respuestas neuronales son invariantes a cualidades como posición, tamaño, iluminación, la orientación de la abuela, o cómo está vestida ella, etc.

Asimismo, la rapidez del tiempo de reacción con la que los humanos fueron capaces de clasificar estos objectos–apenas tiempo suficiente para que algunos picos pasen–demuestra que es posible realizar esta tarea sin el tiempo adicional requerido para operaciones recurrentes más complejas. Más bien, esto es un proceso de un solo pase hacia adelante (single feed-forward).

Estas ideas sugirieron que podríamos desarrollar una arquitectura de red neuronal que sea completamente hacia adelante, pero que al mismo tiempo fuera capaz de resolver el problema de reconocimiento en una manera que sea invariante a transformaciones irrelevantes de las señales de entrada.

Una idea más proveniente del cerebro humano viene de Gallant y Van Essen, cuyo modelo del cerebro ilustra dos caminos distintos:

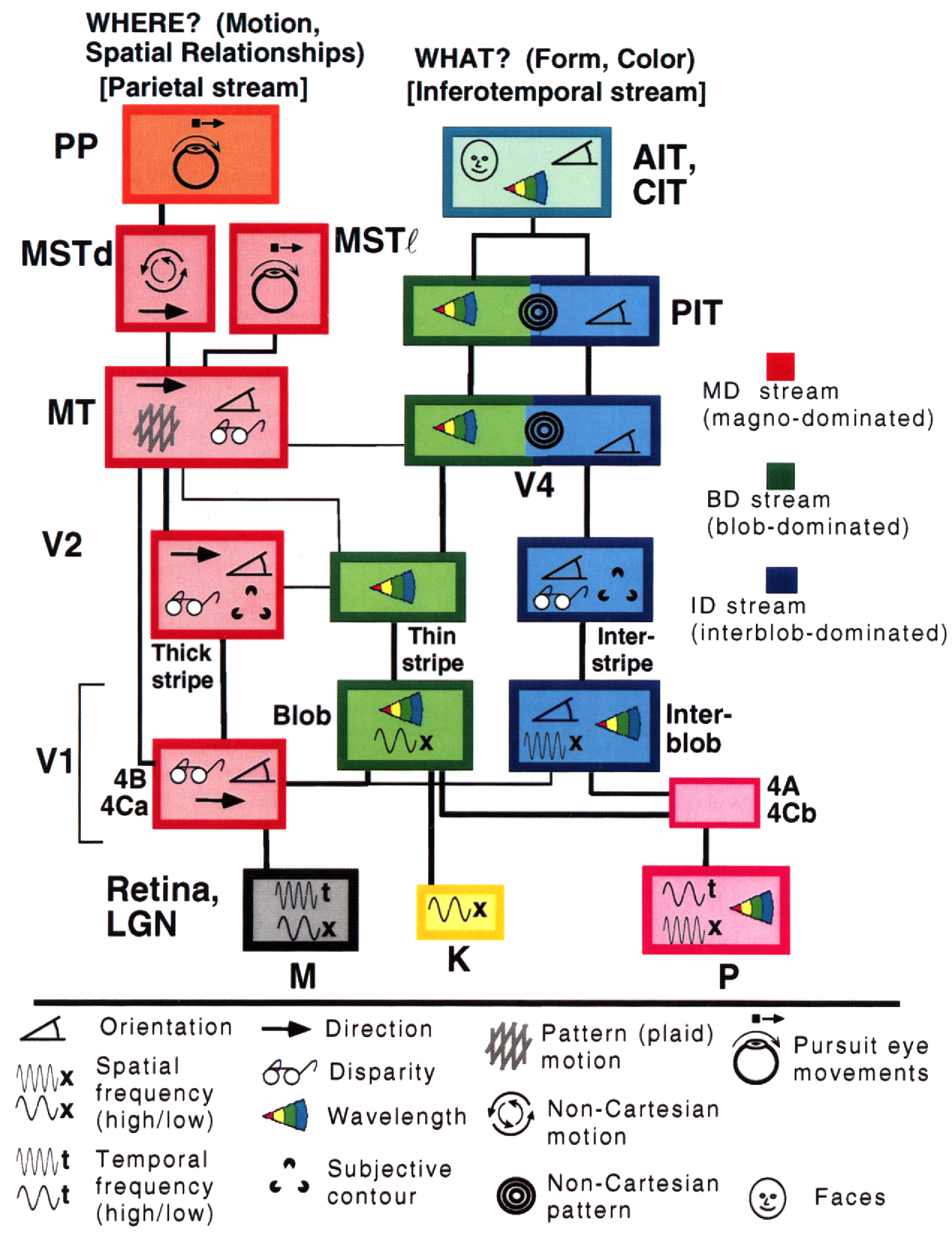
El lado derecho representa el camino ventral, el cual indica qué se está viendo, mientras que el lado izquierdo representa el camino dorsal, el cual identifica ubicaciones, geometría y movimiento. Parecen ser relativamente independientes (con algunas interacciones entre sí, por supuesto) en el córtex visual del humano (y del primate)

Contribuciones de Hubel y Wiesel (1962)

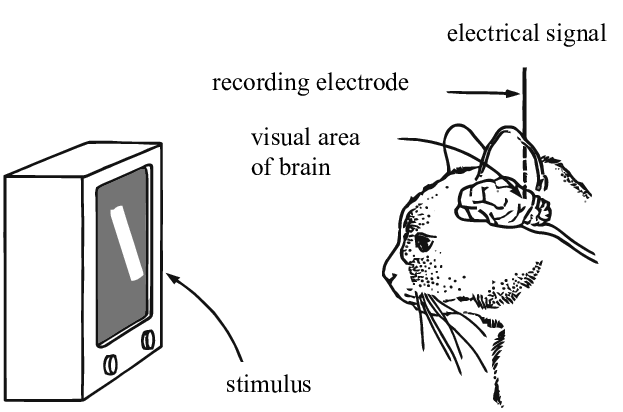
En sus experimentos, Hubel y Wiesel utilizaron electrodos para medir activaciones neuronales en respuesta a estímulos visuales en cerebros de gatos. Con estos, descubrieron que las neuronas en la región V1 son sensibles únicamente a ciertas zonas de un campo visual (llamadas “campos receptores”) y detectan bordes orientados. Por ejemplo, Hubel y Wiesel demostraron que si muestras a un gato una barra vertical y comienzas a rotarla, a un ángulo dado la neurona se activará. De manera similar, cuando esta barra se aleja de ese ángulo, la activación de la neurona decrece. A estas neuronas de activación selectiva Hubel y Wiesel las llamaron “células simples”, por su habilidad para detectar patrones locales.

Ellos también descubrieron que si se aleja la barra del campo receptor, esa neurona en particular dejará de activarse, pero alguna otra lo hará. Existen detectores de patrones locales que corresponden a todas las áreas del campo visual, y de ahí la idea de que el cerebro humano procesa la información visual como una colección de “convoluciones”.

Otro tipo de neurona, a la que ellos nombraron “célula compleja”, acumula la salida de múltiples células simples dentro de un área determinada. Podemos pensar que estas células calculan una acumulación de las activaciones utilizando una función como máximo, suma, suma de cuadrados o cualquier otra función que no dependa del orden. Estas células complejas detectan bordes y orientaciones en una región, sin importar en dónde se encuentran estos estímulos dentro de la región. En otras palabras, son invariantes al desplazamiento con respecto a pequeñas variaciones en las posiciones de la entrada.

Contribuciones de Fukushima (1982)

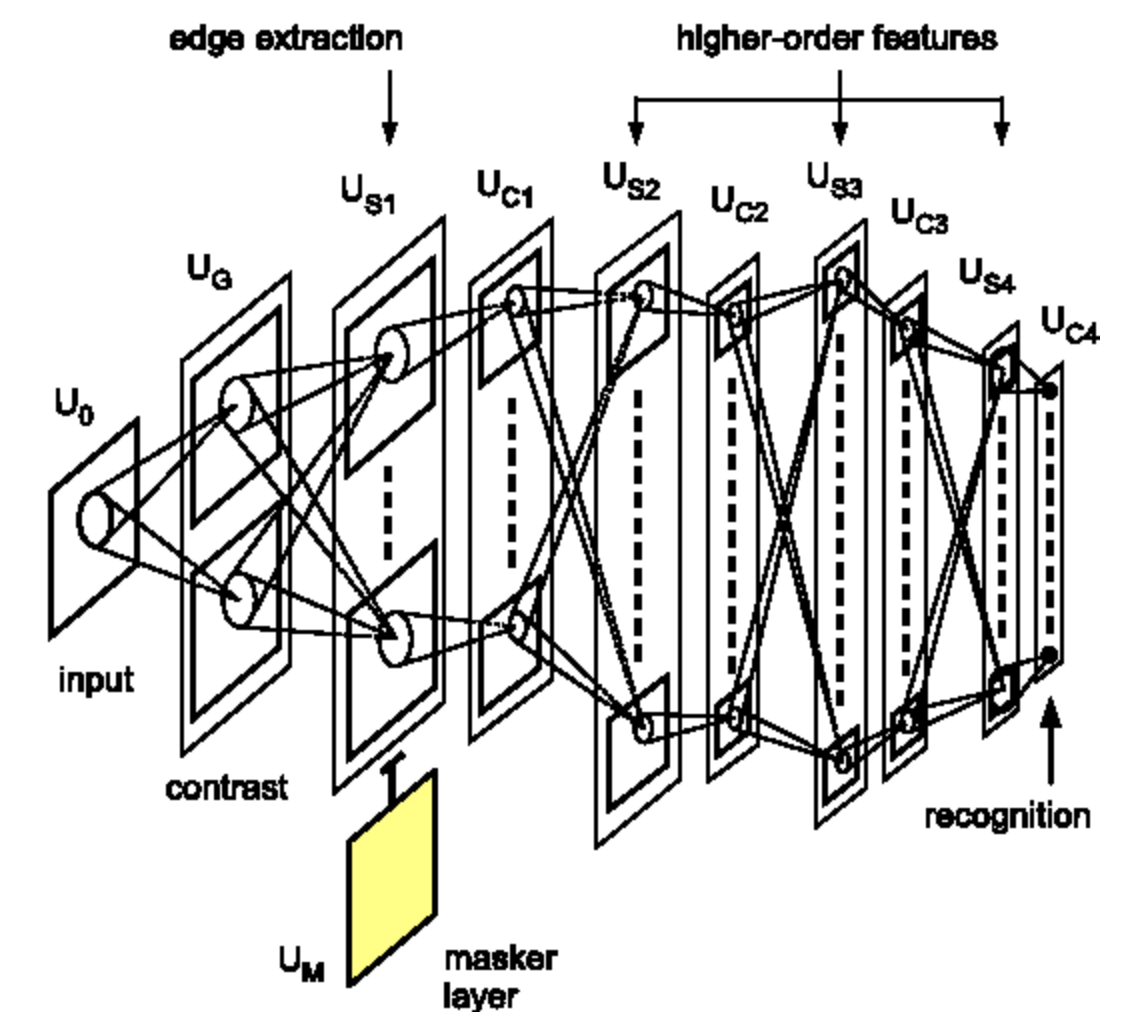
Fukushima fue el primero en implementar con modelos computacionales la idea de capas múltiples de células simples y complejas utilizando un conjunto de datos de dígitos escritos a mano. Algunos de estos detectores de características eran hechos a mano o aprendidos. Aunque el aprendizaje usaba algoritmos de agrupamiento no supervisado, entrenados para cada capa de forma separada debido a que aún no se utilizaba la retropropagación.

Algunos años después (1989, 1998), Yann LeCun implementó la misma arquitectura, pero esta vez entrenó los detectores en una forma supervisada utilizando retropropagación. Esto es considerado ampliamente como el nacimiento de las redes neuronales convolucionales modernas. (Nota: Riesenhuber en 1999 en el MIT también redescubrió esta arquitectura. Sin embargo, él no utilizó retropropagación).