Redes Neuronales Artificiales (ANNs)

🎙️ Alfredo Canziani

Aprendizaje supervisado para clasificación

• Considere la Fig. 1(a) de abajo. Los puntos de este gráfico se encuentran en las ramas de la espiral, y viven en $\R^2$. Cada color representa una etiqueta de clase. El número de clases únicas es $K = 3$. Esto es representado matemáticamente por la Ec. 1(a).

• Fig. 1(b) muestra una espiral similar, con un término añadido de ruido Gaussiano. Esto es representado matemáticamente por la Ec. 1(b).

En ambos casos, estos puntos no son linealmente separables.

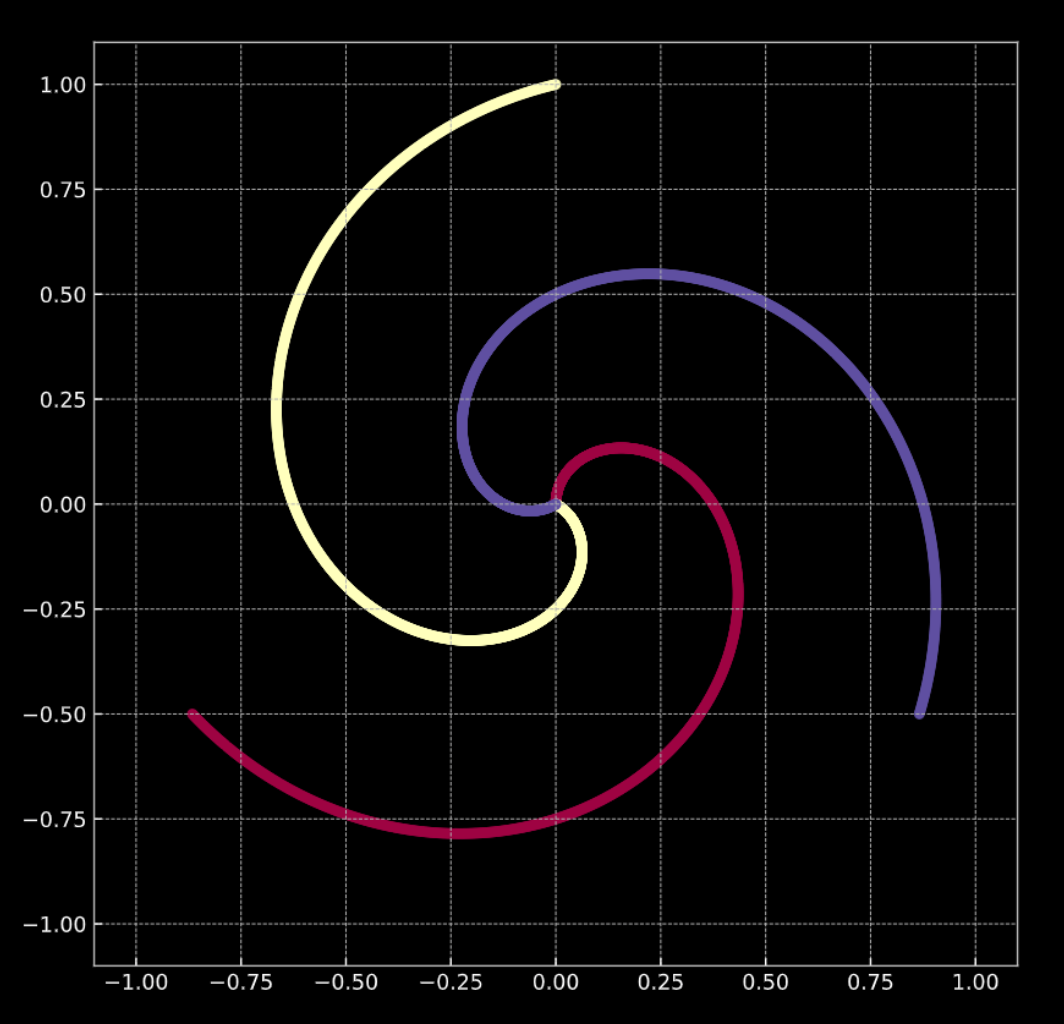Fig. 1(a) Espiral "limpia" en 2D

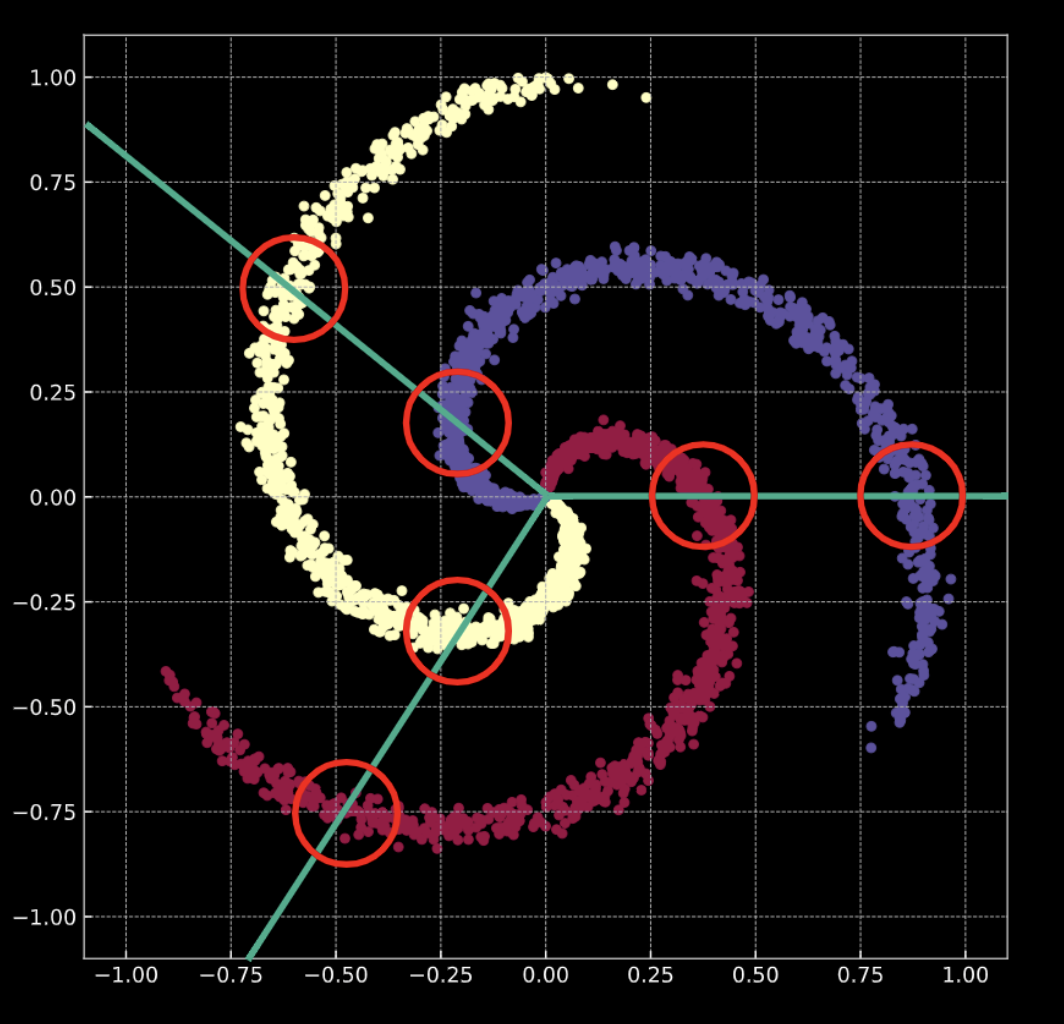Fig. 1(b) Espiral "ruidosa" en 2D

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\] Ec. 1(a) \[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] Ec. 1(b)

¿Qué significa realizar clasificación? Considere el caso de regresión logística. Si la regresión logística para clasificación es aplicada a estos datos, creará un conjunto de planos lineales (fronteras de decisión) en un intento de separar los datos en sus clases. El problema con esta solución es que en cada región existen puntos que pertenecen a múltiples clases. Las ramas de la espiral cruzan las fronteras de decisión lineales. Esta no es una gran solución!

¿Cómo arreglamos esto? Transformamos el espacio de entrada de tal manera que los datos son forzados a ser linealmente separables. Para hacer esto, durante el transcurso del entrenamiento de una red neuronal las fronteras de decisión que aprenda tratarán de adaptarse a la distribución de los datos de entrenamiento.

Nota: Una red neuronal siempre se representa desde abajo hacia arriba. La primera capa está en la parte inferior, y la última en la parte superior. Esto se debe a que conceptualmente, los datos de entrada son características de bajo nivel para cualquier tarea que la red neural esté realizando. A medida que los datos se desplazan hacia arriba a través de la red, cada capa subsiguiente extrae características de un nivel más alto.

Datos de entrenamiento

La semana pasada vimos que una red neural recién inicializada transforma su entrada de forma arbitraria. Esta transformación, sin embargo, no es (inicialmente) instrumental para realizar la tarea en cuestión. Ahora exploraremos cómo, usando datos, podemos forzar esta transformación para que tenga algún significado que sea relevante para la tarea en curso. Los siguientes son datos utilizados como entrada de entrenamiento para una red.

• $\vect{X}$ representa los datos de entrada, una matriz de dimensión $m$ (número de datos de entrada de entrenamiento) x $n$ (dimensión de cada punto de entrada). En el caso de los datos mostrados en las Figuras 1(a) y 1(b), $n = 2$.

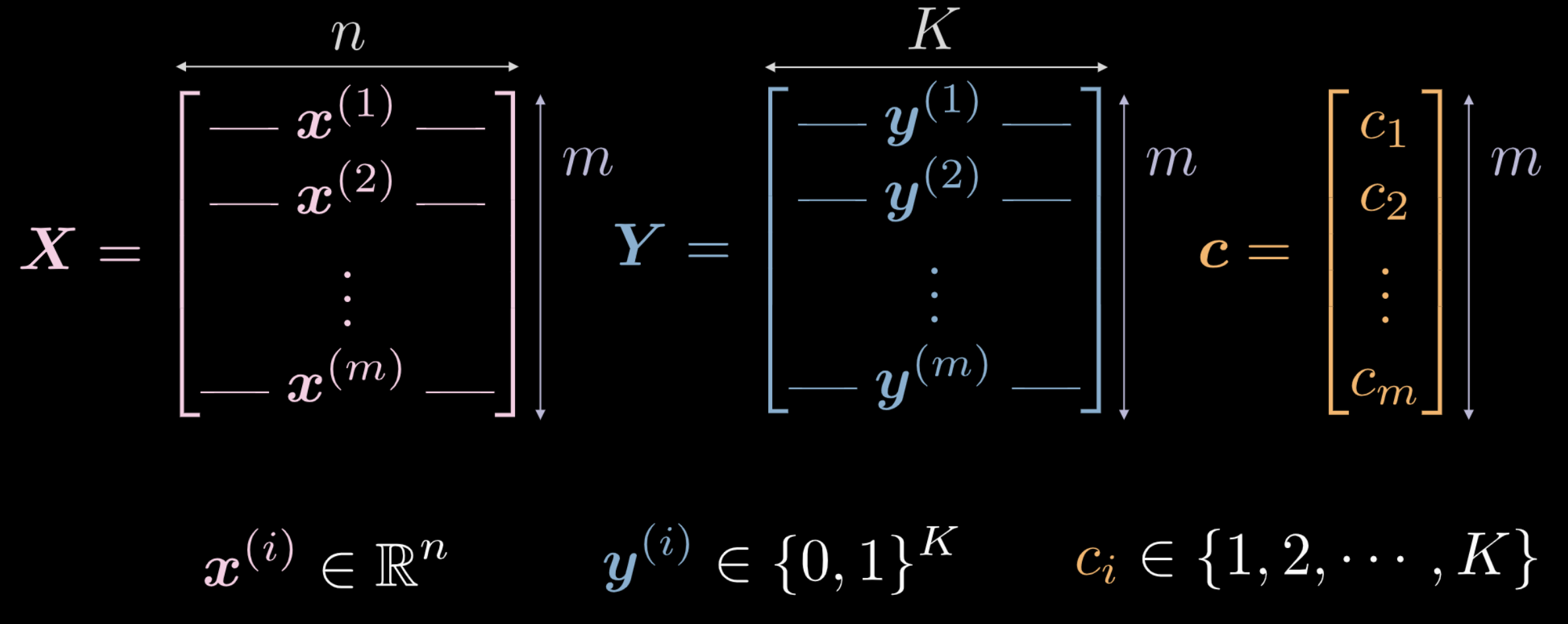
Fig. 2 Datos de entrenamiento

• El vector $\vect{c}$ y la matriz $\boldsymbol{Y}$ representan etiquetas de clase para cada uno de los $m$ puntos de datos. En el ejemplo anterior, hay $3$ clases diferentes.

• $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, y $\vect{c} \in \R^m$. Sin embargo, no podemos usar $\vect{c}$ como datos de entrenamiento. Si usamos etiquetas de clase numéricas distintas $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, la red puede inferir un orden dentro de las clases que no es representativo de la distribución de los datos.
• Para evitar este problema, usamos una codificación one-hot. Para cada etiqueta $c_i$, se crea un vector nulo $K$-dimensional $\vect{y}^{(i)}$, en el cual el elemento $c_i$-ésimo es establecido en $1$ (ver Fig. 3 de abajo).

Fig. 3 Codificación *one hot*

• Por lo tanto, $\boldsymbol Y \in \R^{m \times K}$. Esta matriz también puede ser pensada como que contiene una masa probabilística, que está totalmente concentrada en uno de los $K$ puntos.

Capas totalmente conectadas (FC)

Ahora veremos lo que es una red completamente conectada (FC) y cómo funciona.

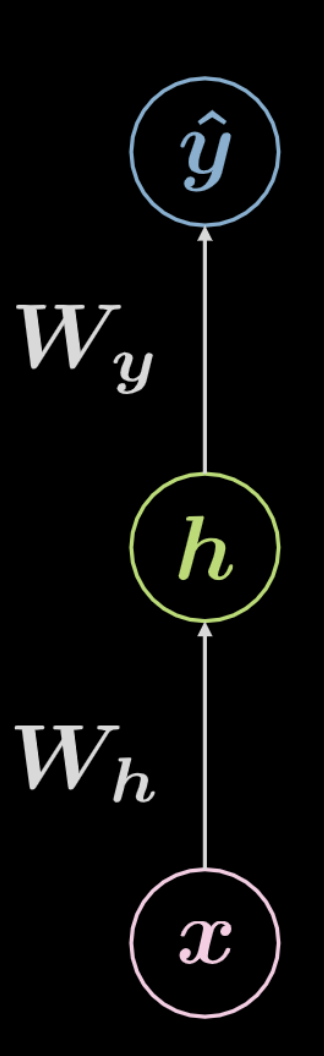
Fig. 4 Red neuronal totalmente conectada

Considere la red que se muestra arriba en la Fig. 4. Los datos de entrada, $\boldsymbol x$, están condicionados a una transformación afín definida por $\boldsymbol W_h$, seguida de una transformación no lineal. El resultado de esta transformación no lineal se denota como $\boldsymbol h$, representando una salida oculta, es decir, una que no se ve desde fuera de la red. Esto es seguido por otra transformación afín ($\boldsymbol W_y$), seguida por otra transformación no lineal. Esto produce la salida final, $\boldsymbol{ \hat{y}}$. Esta red puede ser representada matemáticamente por las ecuaciones en Ec. 2 a continuación. \(f\) y \(g\) son ambas no linealidades.

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] Ec. 2 Las matemáticas detrás de la red totalmente conectada

Una red neuronal básica como la que se muestra arriba es simplemente un conjunto de pares sucesivos, siendo cada par una transformación afín seguida de una operación no lineal (aplastamiento). Entre las funciones no lineales que se utilizan con frecuencia se encuentran la ReLU, la sigmoidea, la tangente hiperbólica y la softmax.

La red que se muestra arriba es una red de 3 capas:

1. neurona de entrada
2. neurona oculta
3. neurona de salida

Por lo tanto, una red neuronal de $3$ capas tiene $2$ transformaciones afines. Esto puede ser extrapolado a una red de $n$ capas.

Ahora pasemos a un caso más complicado.

Hagamos un caso de 3 capas ocultas, completamente conectadas en cada capa. Una ilustración se puede encontrar en la Fig. 5

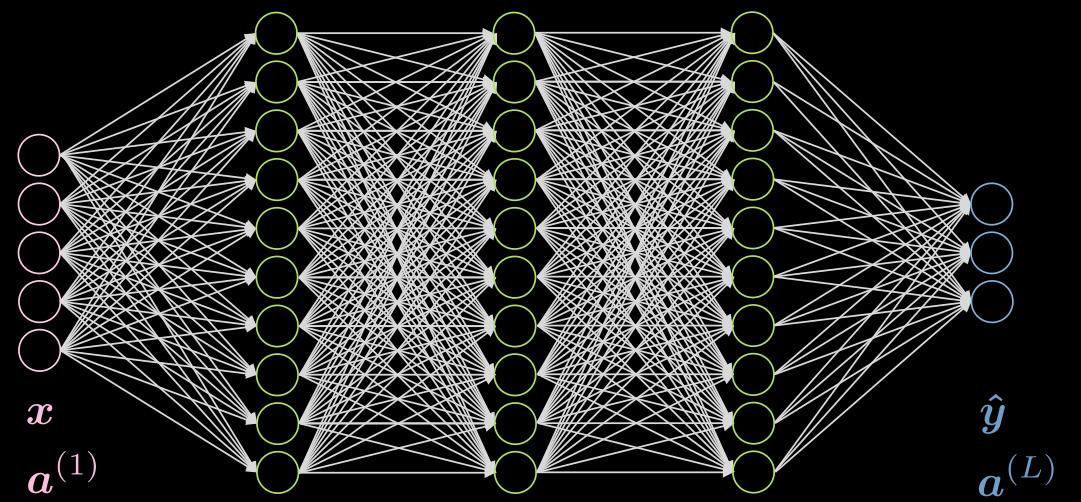
Fig. 5 Red neuronal con 3 capas ocultas

Consideremos la neurona $j$ en la segunda capa. Su activación es:

\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]

donde $\vect{w}^{(j)}$ es la $j$-ésima fila de $\vect{W}^{(1)}$.

Nótese que la activacion de la capa de entrada en este caso es únicamente la identidad. Las capas ocultas pueden tener activaciones como ReLU, tangente hiperbólica, sigmoide, soft (arg)max, etc.

La activación de la última capa en general dependeráde su caso de uso, como se explica en este anuncio de Piazza.

Red neuronal (inferencia)

Pensemos de nuevo en la red neural de tres capas (entrada, oculta, salida), como se ve en la Fig. 6

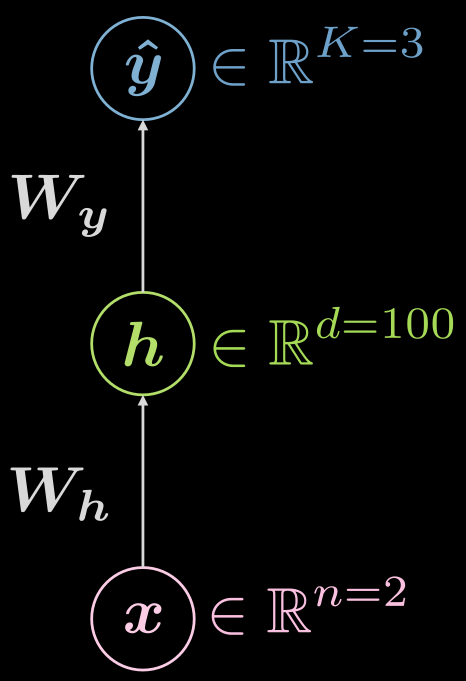
Fig. 6 Red neuronal de tres capas

¿Qué tipo de funciones estamos viendo?

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

Sin embargo, es útil visualizar el hecho de que hay una capa oculta, y el mapeo puede ser ampliado como:

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

¿Cómo podría ser un ejemplo de configuración para el caso anterior? En este caso, se tiene una entrada de dimensión dos ($n=2$), la única capa oculta podría tener una dimensión de 1000 ($d = 1000$), y tenemos 3 clases ($C=3$). Hay buenas razones prácticas para no tener demasiadas neuronas en una capa oculta, por lo que podría tener sentido dividir esa única capa oculta en 3 con 10 neuronas cada una ($1000 \rightarrow 10 \times 10 \times 10$).

Red neuronal (entrenamiento I)

Entonces, ¿cómo luce el típico entrenamiento? Es útil formular esto en la terminología estándar de costo.

En primer lugar, volvamos a introducir el soft (arg)max y declaremos explícitamente que es una función de activación común para la última capa, cuando se utiliza el costo log-likelihood negativo, en los casos de predicción de múltiples clases. Como dijo el profesor LeCun en su lección, esto se debe a que se obtienen mejores gradientes que si se utilizaran los sigmoides y el costo cuadrático. Además, su última capa ya estará normalizada (la suma de todas las neuronas de la última capa será $1$), de una manera que es más favorable para los métodos de gradientes que la normalización explícita (dividiendo por la norma).

El soft (arg)max dará logits en la última capa que se ven así:

\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]

Es importante señalar que el conjunto no está cerrado debido a la naturaleza estrictamente positiva de la función exponencial.

Dado el conjunto de las predicciones $\matr{\hat{Y}}$, el costo será:

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]

Acá c denota la etiqueta entera, no la representación de codificación one-hot.

Hagamos dos ejemplos, uno en el que un ejemplo esté clasificado correctamente, y otro en el que no lo esté.

Digamos que

\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]

¿Cuál es el costo por instancia?

Para el caso de una predicción casi perfecta ($sim$ significa aproximadamente):

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]

Para el caso de casi absolutamente equivocado:

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]

Observe en los ejemplos anteriores, $\sim 0 \rightarrow 0^{+}$ y $\sim 1 \rightarrow 1^{-}$. ¿Por qué es así? Tómate un minuto para pensar.

Nota: Es importante saber que si usas CrossEntropyLoss, obtendrás LogSoftMax y el NLLLoss Loglikelihood negativo juntos, ¡así que no lo hagas dos veces!

Red neuronal (entrenamiento II)

Para el entrenamiento, agregamos todos los parámetros entrenables – matrices de peso y sesgos – en una colección que llamamos $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$. Esto nos permite escribir la función objetivo o de costo como:

\[J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]

Esto hace que el costo dependa de la salida de la red $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$, de modo que podemos convertir esto en un problema de optimización.

Una simple ilustración de cómo funciona esto se puede ver en la Fig. 7, donde $J(\vartheta)$, la función que necesitamos minimizar, tiene sólo un parámetro escalar $\vartheta$.

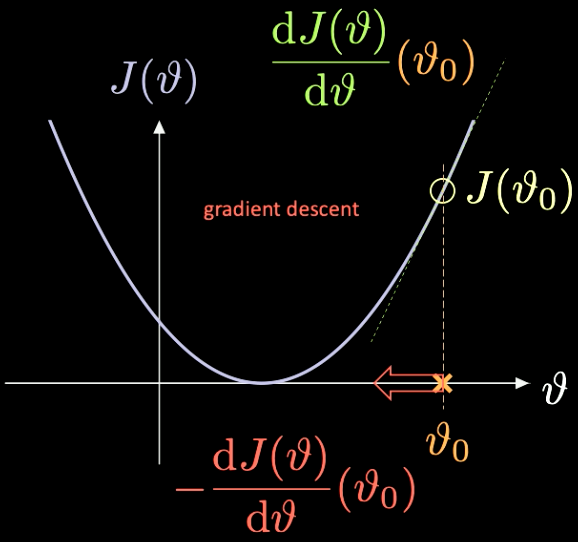
Fig. 7 Optimización de una función de costo mediante descenso de gradiente.

Escogemos un punto de inicialización aleatorio $\vartheta_0$ – con el costo asociado $J(\vartheta_0)$. Podemos calcular la derivada evaluada en ese punto $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$. En este caso, la pendiente de la derivada es positiva. Así que tenemos que dar un paso en la dirección del descenso más pronunciado. En este caso, eso es $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$.

La repetición iterativa de este proceso se conoce como descenso de gradiente. Los métodos de gradiente son las herramientas principales para entrenar una red neuronal.

Para calcular los gradientes necesarios, tenemos que usar la propagación hacia atrás

\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]

Clasificación en la espiral - Jupyter notebook

El Jupyter notebook se puede encontrar aquí. Para ejecutar el notebook, asegúrese de tener instalado el entorno del minicurso DL como se especifica en README.md.

Una explicación de cómo usar torch.device() se puede encontrar en notas de la semana pasada.

Como antes, vamos a trabajar con puntos en $\mathbb{R}^2$ con tres etiquetas categóricas diferentes – en rojo, amarillo y azul – como se puede ver en la Fig. 8.

Fig. 8 Datos de clasificación de espirales.

nn.Sequential() es un contenedor que pasa módulos al constructor en el orden en que son añadidos; nn.linear() está mal nombrado porque aplica una transformación afín de los datos entrantes: $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$. Para más información, consulta la documentación de PyTorch.

Recuerda, una transformación afín son cinco cosas: rotación, reflexión, traslación, escalado y shearing.

Como se puede ver en la Fig. 9, al tratar de separar los datos de las espirales con fronteras de decisión lineales – sólo usando módulos nn.linear(), sin una no-linealidad entre ellos – lo mejor que podemos lograr es una precisión del $50\%$.

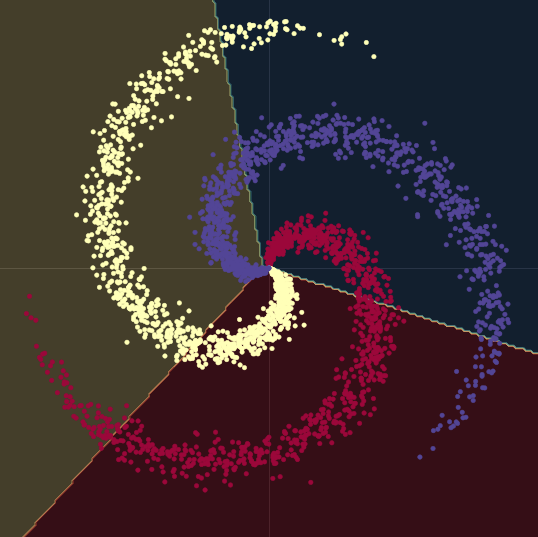
Fig. 9 Fronteras de decisión lineales.

Cuando pasamos de un modelo lineal a uno con dos módulos nn.linear() y un nn.ReLU() entre ellos, la precisión sube al $95\%$. Esto se debe a que las fronteras se vuelven no lineales y se adaptan mucho mejor a la forma espiral de los datos, como se puede ver en la Fig. 10.

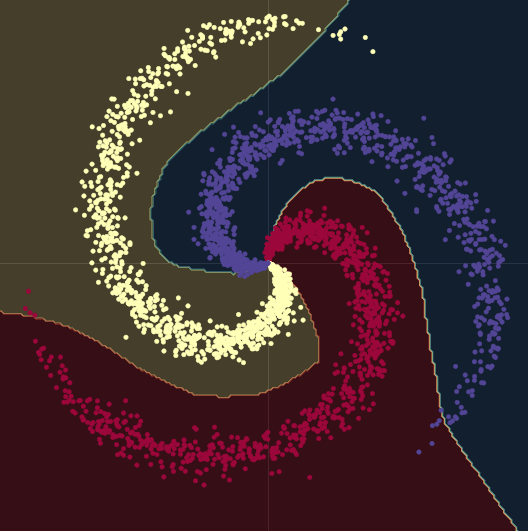
Fig. 10 Fronteras de decisión no lineales.

Un ejemplo de un problema de regresión que no puede ser resuelto correctamente con una regresión lineal, pero que se resuelve fácilmente con la misma estructura de red neuronal puede verse en este cuaderno y en la Fig. 11, que muestra 10 redes diferentes, donde 5 tienen una función de activación nn.ReLU() y 5 tienen una nn.Tanh(). La primera es una función lineal por partes, mientras que la segunda es una regresión continua y suave.

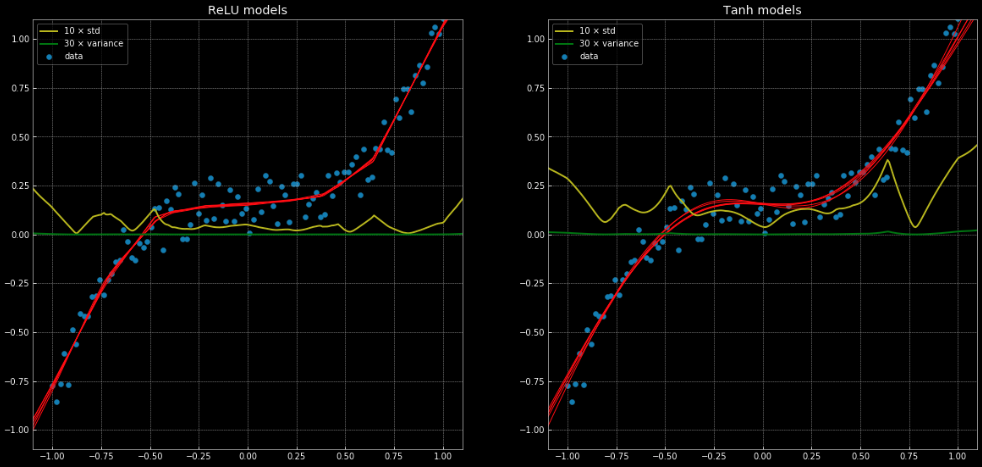
Fig. 11: 10 Redes neuronales, junto con su varianza y desviación estándar.
Izquierda: Cinco redes con ReLU. Derecha: Cinco redes con tanh.

Las líneas amarillas y verdes muestran la desviación estándar y la varianza de las redes. Su uso es útil para algo similar a un “intervalo de confianza” – ya que las funciones dan una única predicción por salida. El uso de la predicción de la varianza del conjunto nos permite estimar la incertidumbre con la que se hace la predicción. La importancia de esto se puede ver en la Fig. 12, donde extendemos las funciones de decisión fuera del intervalo de entrenamiento y estas tienden a $+\infty, -\infty$.

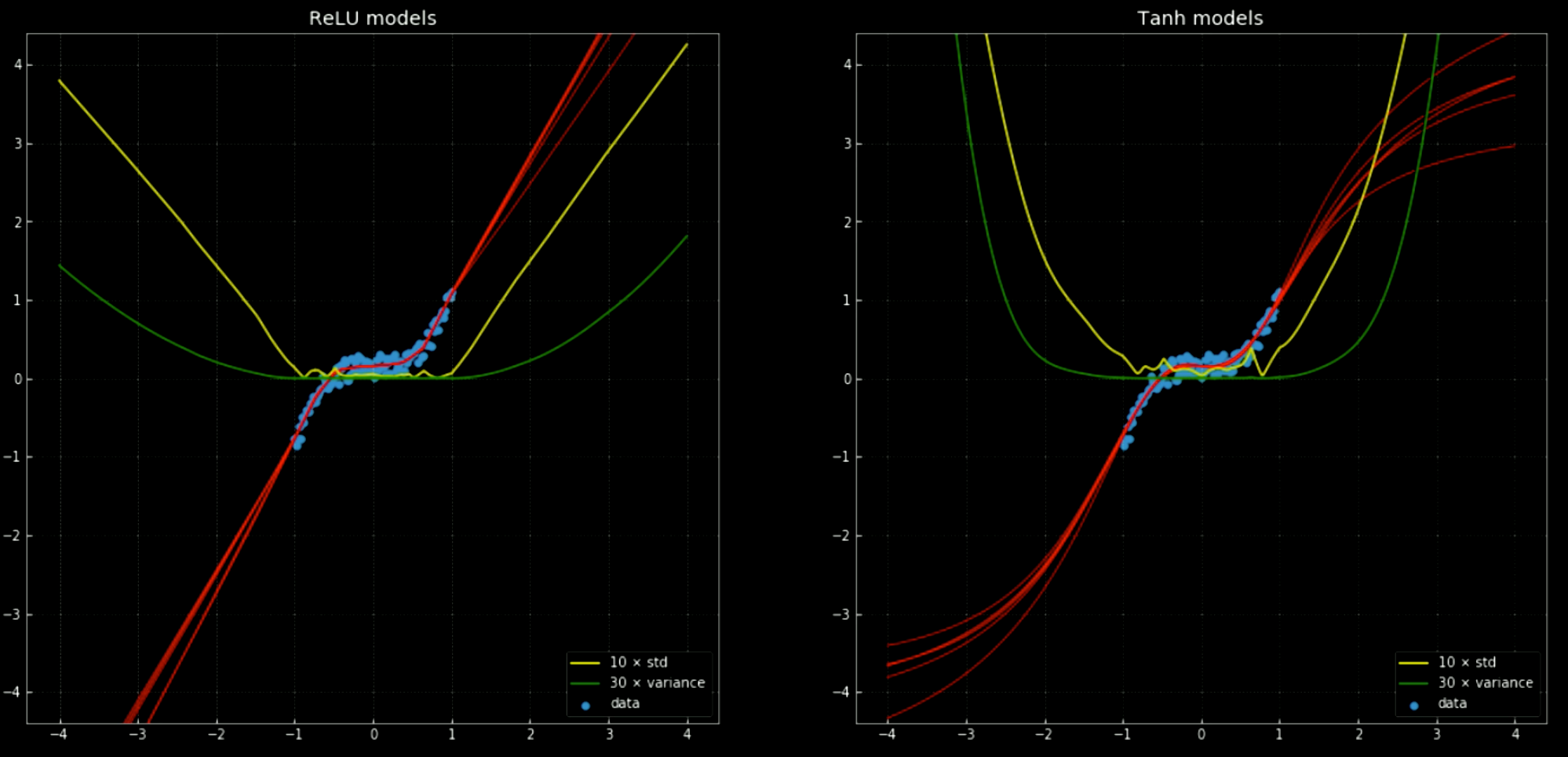
Fig. 12 Redes neuronales con varianza y desviación estándar fuera del intervalo de entrenamiento.
Left: Cinco redes ReLU. Right: Cinco redes tanh.

Para entrenar cualquier Red Neuronal usando PyTorch, se necesitan 5 pasos fundamentales en el ciclo de entrenamiento:

1. output = model(input) es el paso hacia adelante del modelo, que toma la entrada y genera la salida.
2. J = loss(output, target <or> label) toma la salida del modelo y calcula el costo de entrenamiento con respecto a la etiqueta real u objetivo.
3. model.zero_grad() limpia los cálculos de gradiente, para que no se acumulen para el siguiente paso.
4. J.backward() hace la propagación hacia atrás y la acumulación: Calcula $\nabla_\texttt{x} J$ por cada variable$\texttt{x}$ para la que hemos especificado requires_grad=True. Estos se acumulan en el gradiente de cada variable: $\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$.
5. optimiser.step() da un paso en el descenso del gradiente: $\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$.

Cuando se entrena a un NN, es muy probable que se necesiten estos 5 pasos en el orden en que fueron presentados.

---

andrescastro-itm
4 Feb 2020