Calcular los gradientes para los módulos NN y los trucos prácticos para la propagación hacia atrás

Un ejemplo concreto de propagación hacia atrás e introducción a módulos básicos de redes neuronales

Ejemplo

A continuación consideramos un ejemplo concreto de propagación hacia atrás asistido por un grafo visual. La función arbitraria $G(w)$ es ingresada en la función de costo $C$, la cual puede ser representada como un grafo. A través de la manipulación de la multiplicación de las matrices Jacobianas, podemos transformar este grafo en el grafo que calculará los gradientes en el sentido contrario (de atrás hacia adelante). (Note que PyTorch y TensorFlow hacen esto automáticamente para el usuario, i.e. el grafo hacia adelante es “reversado” automáticamente para crear el grafo de derivadas que propaga hacia atrás el gradiente).

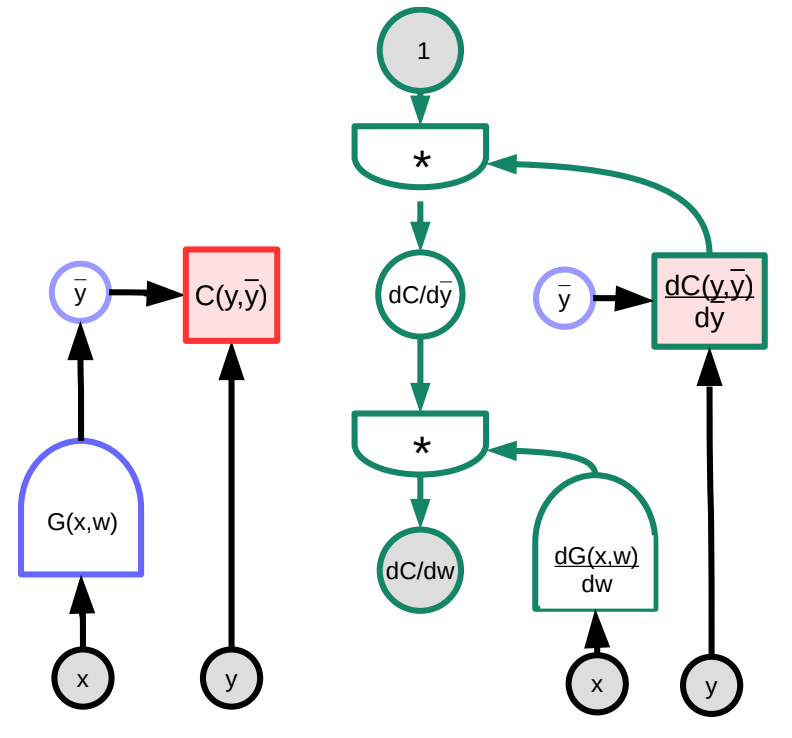
En este ejemplo, el grafo verde de la derecha representa el grafo de gradientes. Siguiendo el grafo desde el nodo superior, se tiene que

En términos de dimensiones, $\frac{\partial C(y,\bar{y})}{\partial w}$ es un vector fila de tamaño $1\times N$, donde $N$ es el número de componentes de $w$; $\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ es un vector fila de tamaño $1\times M$, donde $M$ es la dimensión de la salida; $\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ es una matriz de tamaño $M\times N$, donde $M$ es el número de salidas de $G$ y $N$ es la dimensión de $w$.

Obsérvese que pueden surgir complicaciones cuando la arquitectura del grafo no es fija, sino que depende de los datos. Por ejemplo, podríamos elegir el módulo de red neuronal en función de la longitud del vector de entrada. Aunque esto es posible, se hace cada vez más difícil manejar esta variación cuando el número de bucles supera una cantidad razonable.

Módulos básicos de redes neuronales

Existen diferentes tipos de módulos pre-definidos (pre-construidos) además de los familiares módulos Linear y ReLU. Estos son útiles dado que están optimizados de manera única para realizar sus respectivas funciones (contrario a estar construidos como una combinación de otros módulos elementales).

• Linear: $Y=W\cdot X$

• ReLU: $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{De otro modo} \end{cases}\]

• Duplicar: $Y_1=X$, $Y_2=X$

  • Como un “divisor Y” donde ambas salidas son iguales a la entrada.

  • Al propagar hacia atrás, los gradientes se suman

  • Puede ser divididos en $n$ ramas de manera similar

    \[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]

• Suma: $Y=X_1+X_2$

  • Si se suman dos variables, cuando una es perturbada, la salida será perturbada por la misma cantidad, i.e.

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{y}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• Max: $Y=\max(X_1,X_2)$

  • Dado que esta función también puede representarse como

• • Por lo tanto, por regla de la cadena,

LogSoftMax vs SoftMax

SoftMax, que también es un módulo de PyTorch, es una forma conveniente de transformar un grupo de números en un grupo de números positivos entre $0$ y $1$ que suman uno. Estos números pueden ser interpretados como una distribución de probabilidad. Por consiguiente, se utiliza comúnmente en los problemas de clasificación. $y_i$ en la siguiente ecuación es un vector de probabilidades para todas las categorías.

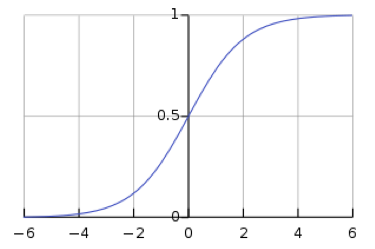
Sin embargo, el uso de softmax deja la red susceptible a desvanecimiento de gradientes. El desvanecimiento de gradiente es un problema, ya que impide que los pesos que se encuentran descendiendo sean modificados por la red neuronal, lo que puede detener completamente que la red neuronal siga entrenándose. La función sigmoide logística, que es la función de softmax para un valor, muestra que cuando $s$ es grande, $h(s)$ es $1$, y cuando $s$ es pequeña, $h(s)$ es $0$. Debido a que la función sigmoide es plana en $h(s) = 0 $ y $h(s) = 1$, el gradiente es $0$, lo que resulta en un gradiente que se desvanece.

A los matemáticos se les ocurrió la idea de logsoftmax para resolver el problema de desvanecimiento de gradiente generado por el softmax. LogSoftMax es otro módulo básico en PyTorch. Como se puede ver en la siguiente ecuación, LogSoftMax es una combinación de softmax y log.

La siguiente ecuación demuestra otra forma de ver la misma ecuación. La figura de abajo muestra la parte $\log(1 + \exp(s))$ de la función. Cuando $s$ es muy pequeña, el valor es $0$, y cuando $s$ es muy grande, el valor es $s$. Como resultado, no se satura, y se evita el problema del desvanecimiento del gradiente.

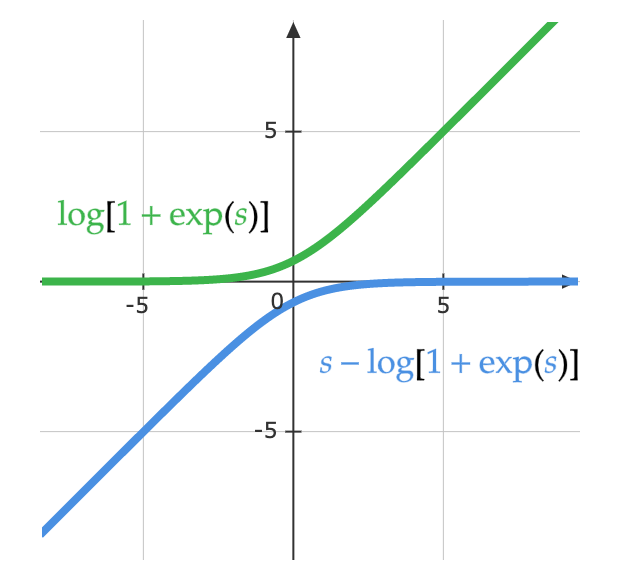
Trucos prácticos para la propagación hacia atrás

Usar ReLU como la función de activación no lineal

ReLU funciona mejor para redes con muchas capas, lo que ha hecho que alternativas como la función sigmoide y la función tangente hiperbólica $\tanh(\cdot)$ pierdan popularidad (dejen de ser usadas). La razón por la que ReLU funciona mejor es probablemente debido a su única torcedura que lo hace equivariante a la escala.

Usar pérdida de entropía cruzada (cross-entropy loss) como la función objetivo para problemas de clasificación

Log softmax, el cual se ha discutido anteriormente en la lección, es un caso especial de pérdida de entropía cruzada. En PyTorch, asegúrese de proporcionar la función de pérdida de entropía cruzada con log softmax como entrada (a diferencia de la softmax normal).

Usar descenso de gradiente estocástico (SGD) sobre minibatches durante el entrenamiento

Como se discutió anteriormente, los minibatches permiten entrenar más eficientemente porque hay redundancia en los datos; no debería ser necesario hacer una predicción y calcular la pérdida en cada observación en cada paso para estimar el gradiente.

Mezclar el orden de los ejemplos de entrenamiento cuando se utiliza descenso de gradiente estocástico (SGD)

El orden importa. Si el modelo sólo ve ejemplos de una sola clase durante cada paso del entrenamiento, entonces aprenderá a predecir esa clase sin aprender por qué debería estar prediciendo esa clase. Por ejemplo, si estuviera tratando de clasificar los dígitos del conjunto de datos MNIST y los datos no estuvieran desordenados, los parámetros de sesgo en la última capa simplemente predecirían siempre el cero, y luego se adaptarían para predecir siempre el uno, luego el dos, etc. Lo ideal sería tener muestras de cada clase en cada minibatch.

Sin embargo, hay un debate en curso sobre si es necesario cambiar el orden de las muestras en cada ciclo (época).

Normalizar las entradas para que tengan media cero y varianza unitaria

Antes del entrenamiento, es útil normalizar cada característica de entrada de modo que tenga una media de cero y una desviación estándar de uno. Cuando se utilizan datos de imágenes RGB, es comun calcular la media y desviación estándar de cada canal individualmente y normalizar la imagen canal por canal. Por ejemplo, tome la media $m_b$ y a desviación estándar $\sigma_b$ de todos los valores de azul del conjunto de datos, luego normalice los valores de azul para cada imagen individual como

donde $\epsilon$ es un número arbitrariamente pequeño que se usa para evitar la división por cero. Se debe hacer lo mismo para los canales verde y rojo. Esto es necesario para obtener una señal significativa de las imágenes tomadas con diferente iluminación; por ejemplo, las imágenes iluminadas de día tienen mucho rojo mientras que las imágenes submarinas casi no tienen.

Usar una método para decrementar la tasa de aprendizaje

La tasa de aprendizaje debe disminuir a medida que el entrenamiento avanza. En la práctica, los modelos más avanzados son entrenados usando algoritmos como Adam/Momentum, los cuales adaptan la tasa de aprendizaje en lugar de un simple SGD con una tasa de aprendizaje constante.

Usar regularización L1 y/o L2 para el decaímiento de los pesos

Se puede añadir un costo para valores de pesos grandes a la función de costo. Por ejemplo, usando regularización L2, podemos definir la pérdida $L$ y actualizar los pesos $w$ como sigue:

Para entender por qué esto se llama decaímiento de los pesos, observe que podemos reescribir la fórmula anterior para mostrar que multiplicamos $w_i$ por una constante menor que uno durante la actualización.

To understand why this is called weight decay, note that we can rewrite the above formula to show that we multiply $w_i$ by a constant less than one during the update.

La regularización L1 (Lasso) es similar, excepto que usamos $\sum_i \vert w_i\vert$ en lugar de $\Vert w \Vert^2$.

Básicamente, la regularización trata de decirle al sistema que minimice la función de costo con el vector de peso más corto posible. Con la regularización L1, los pesos que no son útiles se reducen a $0$.

Inicialización de los pesos

Los pesos deben ser inicializados al azar, sin embargo, no deben ser demasiado grandes ni demasiado pequeños, de manera que la salida sea aproximadamente de la misma varianza que la entrada. Existen varios trucos de inicialización de pesos incorporados en PyTorch. Uno de los trucos que funciona bien para los modelos profundos es la inicialización Kaiming, en la que la varianza de los pesos es inversamente proporcional a la raíz cuadrada del número de entradas.

Usar dropout

Dropout es otra forma de regularización. Se puede considerar como otra capa de la red neural: toma las entradas, establece aleatoriamente en cero $n/2$ de las entradas y devuelve el resultado como salida. Esto obliga al sistema a tomar información de todas las unidades de entrada en lugar de depender excesivamente de un pequeño número de unidades de entrada, distribuyendo así la información entre todas las unidades de una capa. Este método fue propuesto inicialmente por Hinton et al (2012).

Para más trucos, ver LeCun et al 1998.

Finalmente, observe que la propagación hacia atrás no funciona únicamente para modelos apilados; también puede funcionar para cualquier grafo acíclico dirigido (DAG) siempre y cuando exista un orden parcial en los módulos.