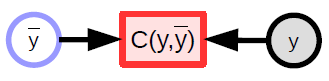Introducción a gradiente descendente y el algoritmo de propagación hacia atrás

Algoritmo de optimización Descenso de Gradiente

Modelos parametrizados

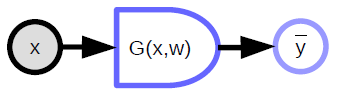
Los modelos parametrizados son simplemente funciones que dependen de entradas y parámetros entrenables. No hay una diferencia fundamental entre los dos, excepto que los parámetros entrenables se comparten entre las muestras de entrenamiento, mientras que la entrada varia de muestra a muestra. En la mayoría de los marcos conceptuales de aprendizaje profundo, los parámetros son implícitos, esto es, que no se indican cuando la función se llama. Se ‘almacenan dentro de la función’, sea dicho, por lo menos en las versiones de modelos orientadas a objetos.

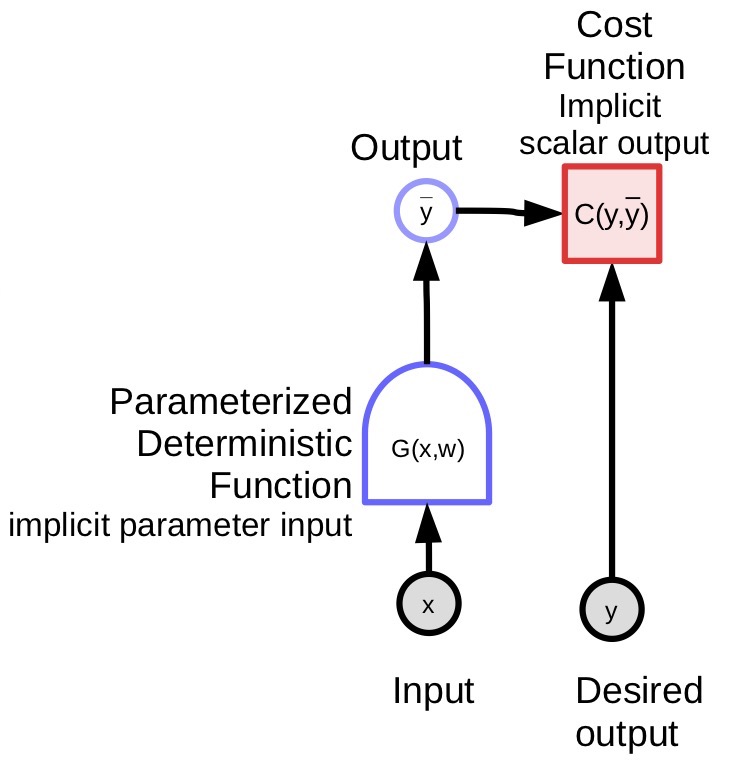
El modelo parametrizado (función) toma una entrada, tiene un vector de parámetros y produce una salida. En el aprendizaje supervisado, esta salida va a la función de costo ($C(y,\bar{y}$)), que compara la verdadera salida (${y}$) con la salida del modelo ($\bar{y}$). La gráfica de cómputo para este modelo se muestra en la Figura 1.

Figure 1: Representación de la gráfica de computación para un Modelo Parametrizado

Ejemplos de funciones parametrizadas

• Modelo Lineal - Suma ponderada de componentes del vector de entrada:

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• Vecino más cercano - Existe una entrada x y una matriz de ponderación W con cada fila de la matriz indexada por k. La salida es el valor de k que corresponde a la fila de W más cercana a x:

  \[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

  Los modelos parametrizados pueden también involucrar funciones complejas.

Notación en diagrama de bloques para gráficas computacionales

• Variables (tensor, escalar, contínua, discreta)
  • es una entrada observada al sistema
  • es una variable calculada que se produce por una función determinista

• Funciones deterministas

  

  • Toman múltiples entradas y pueden producir múltiples salidas.
  • Tienen una variable de parámetro implícita (${w}$)
  • El lado redondeado indica la dirección en la que es fácil de calcular. En el diagrama de arriba, es más fácil calcular ${\bar{y}}$ a partir de ${x}$, que al revés.

• Función escalar

  

  • Se utilizan para representar funciones de costo
    • Tienen una salida escalar implícita
    • Toma múltiples entradas y devuelve un solo valor (usualmente la distancia entre las entradas)

Funciones de pérdida

La función de pérdida es una función que se minimiza durante el entrenamiento. Existen dos tipos de pérdidas:

1) Pérdida por muestra

2) Pérdida promedio -

Para cualquier conjunto de muestras

La pérdida promedio sobre el conjunto $S$ se da por:

Figura 2: Grafo de cómputo para un modelo con pérdida promedio

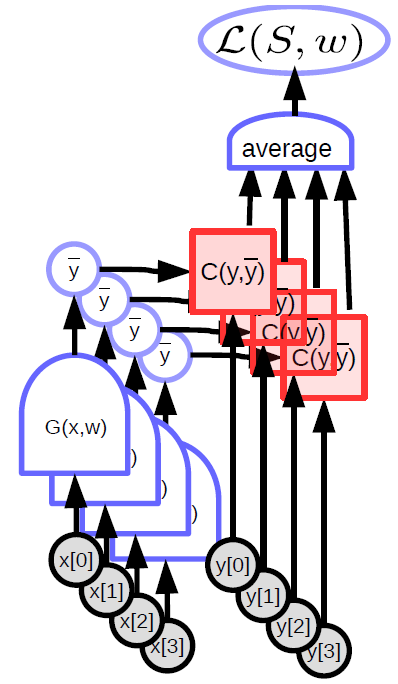En el paradigma estándar de aprendizaje supervisado, la pérdida (por muestra) es simplemente la salida de la función de costo. El aprendizaje automatizado consiste principalmente en optimizar funciones (usualmente minimizarlas). También, puede involucrar encontrar equilibrios de Nash entre dos funciones como es el caso de los GANs. Esto se hace utilizando Métodos Basados en Gradiente, aunque no necesariamente corresponda al Descenso de Gradiente.

Descenso de gradiente

Un Método Basado en Gradiente es un método/algoritmo que halla el mínimo de una función, asumiendo que uno puede fácilmente calcular el gradiente de esa función. Asume que la función es contínua y diferenciable casi en cualquier parte (no necesariamente es diferenciable en cualquier parte).

Intuición en Descenso de Gradiente - Imagine que está en una montaña en la mitad de una noche con niebla. Dado que quiere descender a la aldea y sólo tiene visión limitada, mira alrededor de su vecindad inmediata para hallar la dirección de descenso más rápido y da un paso en esa dirección.

Diferentes métodos de Descenso de Gradiente

• Regla de actualización de Descenso de Gradiente de (lote o “batch”) completo :

  \[w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\]

• Para SGD (Descenso de Gradiente Estocástico), la regla de actualización se convierte en:

  • Seleccione una $p \in \lbrace 0, \cdots, P-1 \rbrace$, entonces actualice

    \[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

donde ${w}$ representa los parámetros a ser optimizados.

$\eta$ acá es una constante, pero en algoritmos más sofisticados, podría ser una matriz.

Si es una matriz semi-definida positiva, aún nos moveremos colina abajo pero no necesariamente en la dirección del descenso más rápido. De hecho, la dirección del descenso más rápido puede no ser siempre la dirección en la que nos queremos mover.

Si la función no es diferenciable, i.e, tiene un agujero, tiene forma de escalera, o es plana, donde el gradiente no da información, uno tiene que recurrir a otros métodos - llamados Métodos de orden 0 o Métodos libres de gradiente. El aprendizaje profundo se trata de Métodos Basados en Gradientes.

Sin embargo, RL (aprendizaje por refuerzo) involucra la Estimación del Gradiente sin la forma explícita del gradiente. Un ejemplo es un robot aprendiendo a montar en bicicleta donde el robot cae de vez en cuando. La función objetivo mide cuánto tiempo la bicicleta permanece sin caer. Desafortunadamente, no existe un gradiente para la función objetivo. El robot necesita intentar diferentes cosas.

La función de costo en RL no es diferenciable la mayor parte del tiempo pero la red que calcula la salida está basada en gradientes. Esta es la principal diferencia entre aprendizaje supervisado y aprendizaje por refuerzo. En este último, la función de costo $C$ no es diferenciable. De hecho es completamente desconocida. Solo devuelve una salida cuando se le dan entradas, como una caja negra. Esto la hace altamente ineficiente lo que es uno de los principales problemas de RL - particularmente cuando el vector de parámetros tiene muchas dimensiones (lo que implica un espacio de solución inmenso para buscar, dificultando buscar hacia donde moverse).

Una técnica popular en RL son los Métodos de Actor Críticos. Un método crítico consiste básicamente de un segundo módulo C, entrenable, que se conoce. Uno puede entrenar el módulo C, que es diferenciable, para aproximar la función de costo/recompenza. La recompenza es un costo negativo, similar a un castigo. Esta es una forma de hacer diferenciable la función de costo, o por lo menos aproximarla con una función diferenciable de forma que se puede hacer retropropagación.

Ventajas de SGD y retropropagación para redes neuronales tradicionales

Ventajas de Descenso de Gradiente Estocástico (SGD)

En la práctica, utilizamos el gradiente estocástico para calcular el gradiente de la función objetivo con respecto a los parámetros. En vez de calcular el gradiente completo de la función objetivo, el cual se promedia entre todas las muestras, el gradiente estocástico solo toma una muestra, calcula la pérdida $L$, y el gradiente de la pérdida con respecto a los parámetros, y después da un paso en la dirección negativa del gradiente.

En la fórmula, $w$ se aproxima como $w$ menos el tamaño de paso, multiplicado por el gradiente de la función de pérdida por muestra con respecto a los parámetros para una muestra dada, ($x[p]$,$y[p]$).

Si hacemos esto en una sola muestra, obtendremos una trayectoria bastante ruidosa, como se muestra en la Figura 3. En vez de que la pérdida se dirija directamente colina abajo, esta es estocástica. Cada muestra dirige la pérdida en una dirección diferente. Es únicamente el promedio que nos dirige al mínimo del promedio. Aunque parece ineficiente, es mucho más rápido que utilizar el gradiente descendente en lotes (batches) por lo menos en el contexto de machine learning cuando las muestras tienen alguna redundancia.

Figura 3: Trayectoria de Descenso de Gradiente Estocástico para actualización por muestra.

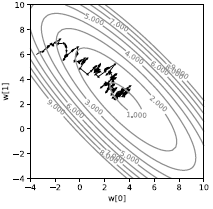En práctica, utilizamos lotes (batches) en vez de hacer un Descenso de Gradiente Estocástico en una única muestra. Calculamos el promedio del gradiente sobre las muestras del lote (batch), no en una sola muestra, y después damos el paso. La única razón para hacer esto es que podemos utilizar de forma más eficiente el hardware existente (i.e. GPUs, CPUs multinúcleo) si utilizamos lotes ya que son más fáciles de paralelizar. El utilizar lotes (Batching) es la forma más simple de paralelizar.

Red Neuronal Tradicional

Las redes neuronales tradicionales son básicamente capas intercaladas de operaciones lineales y operaciones no-lineales punto a punto. Para operaciones lineales, conceptualmente son sólo multiplicaciones matriz-vector. Tomamos el vector de entrada multiplicado por una matriz conformada por los pesos. El segundo tipo de operación es tomar todos los componentes de los vectores de sumas ponderadas y pasarlos a través de una no-linealidad simple (i.e. $\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, …).

Figura 4: Red Neuronal Tradicional

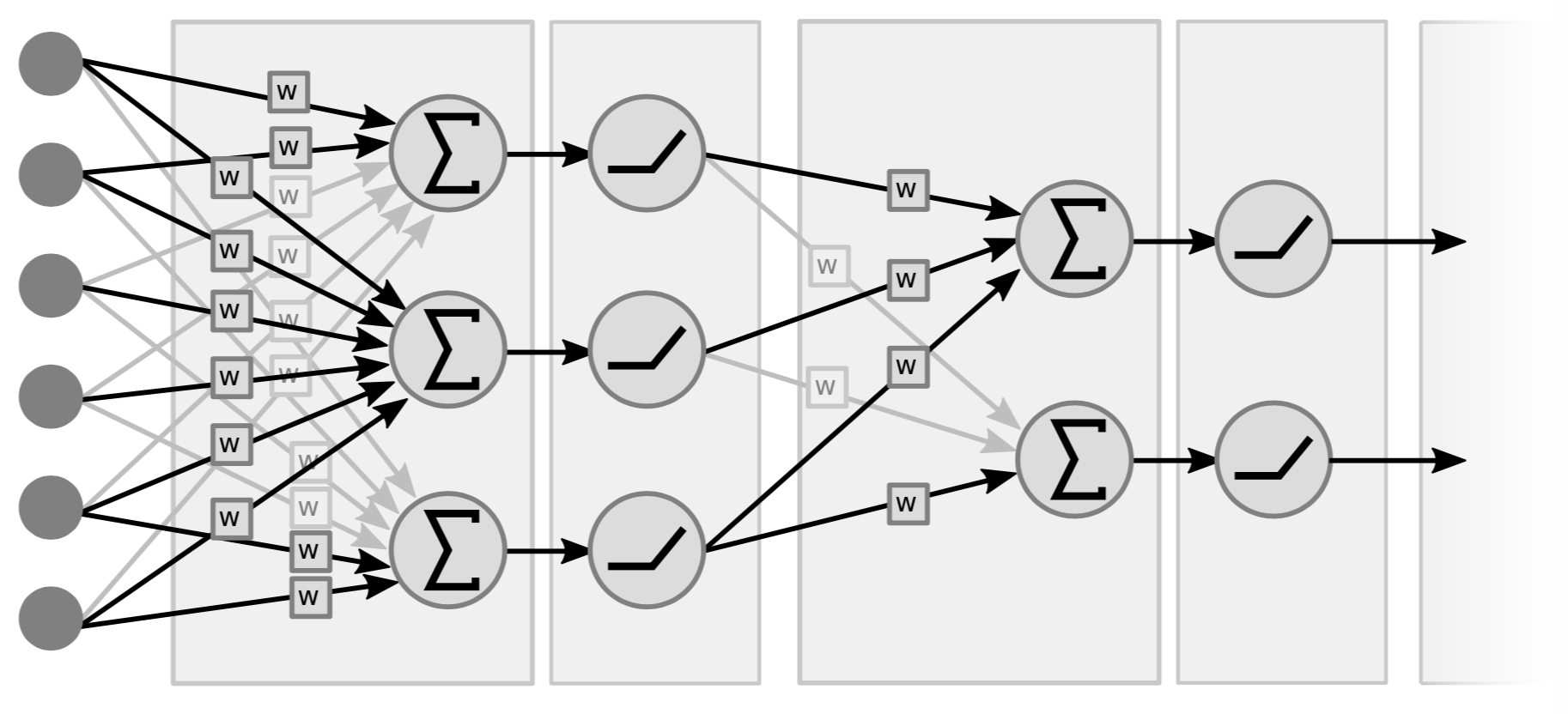La Figura 4 es un ejemplo de una red de 2 capas, porque lo que importa son los pares (i.e lineal + no-lineal). Algunas personas la llaman red de 3 capas porque cuentan las variables. Note que si no hubieran no-linealidades en el medio, podríamos tener también una sola capa porque el producto de dos funciones lineales es una función lineal.

La Figura 5 muestra cómo los bloques funcionales lineales y no-lineales de la red se apilan:

Figura 5: Viendo dentro de los bloques lineales y no-lineales

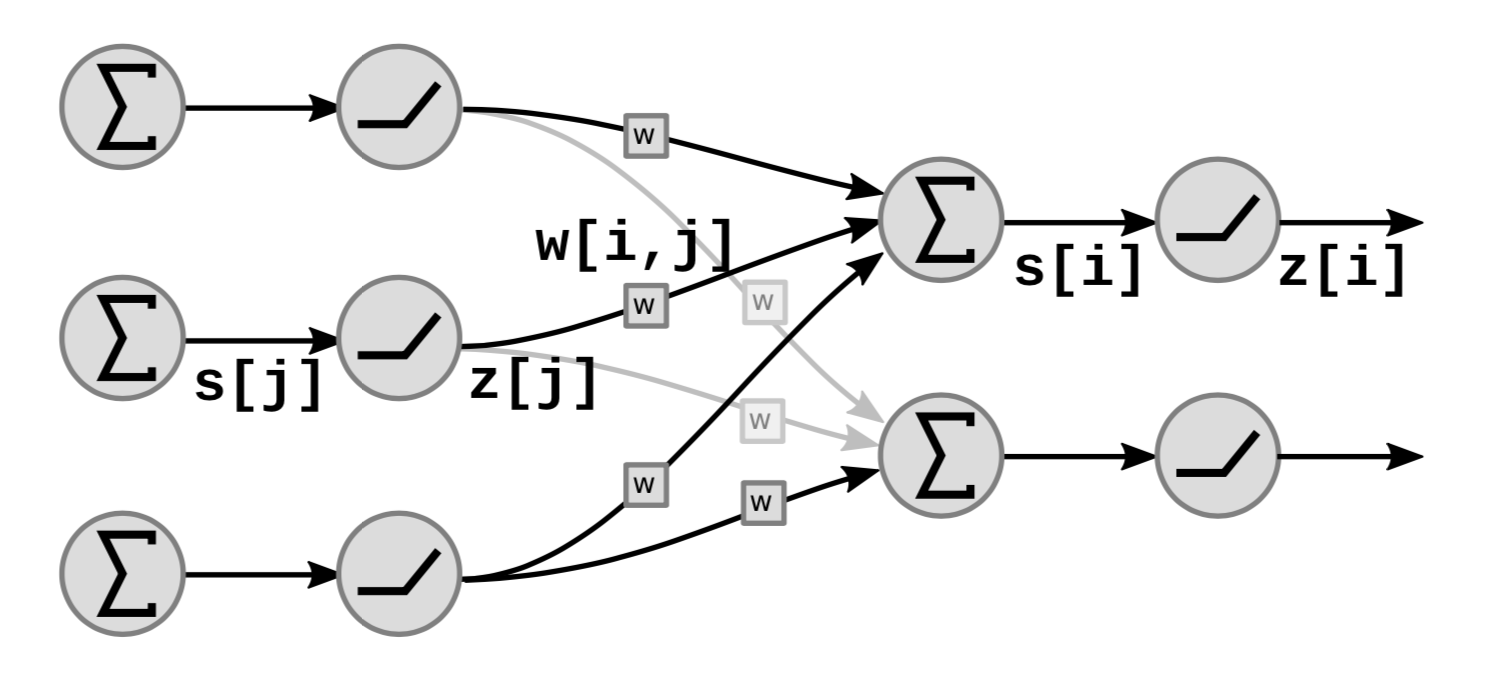En la gráfica, $s[i]$ es la suma ponderada de la unidad ${i}$ que se calcula como:

donde $UP(i)$ denota el predecesor de $i$ y $z[j]$ en la $j$th-ésima salida de la capa anterior.

La salida $z[i]$ se calcula como:

donde $f$ es una función no-lineal.

Retropropagación a través de una función no-lineal

La primera forma de hacer retropropagación es propagar hacia atrás a través de una función no lineal. Tomamos una función no-lineal particular $h$ de la red y dejamos todo lo demás en la caja negra.

Figura 6: Retropropagación a través de una función no-lineal

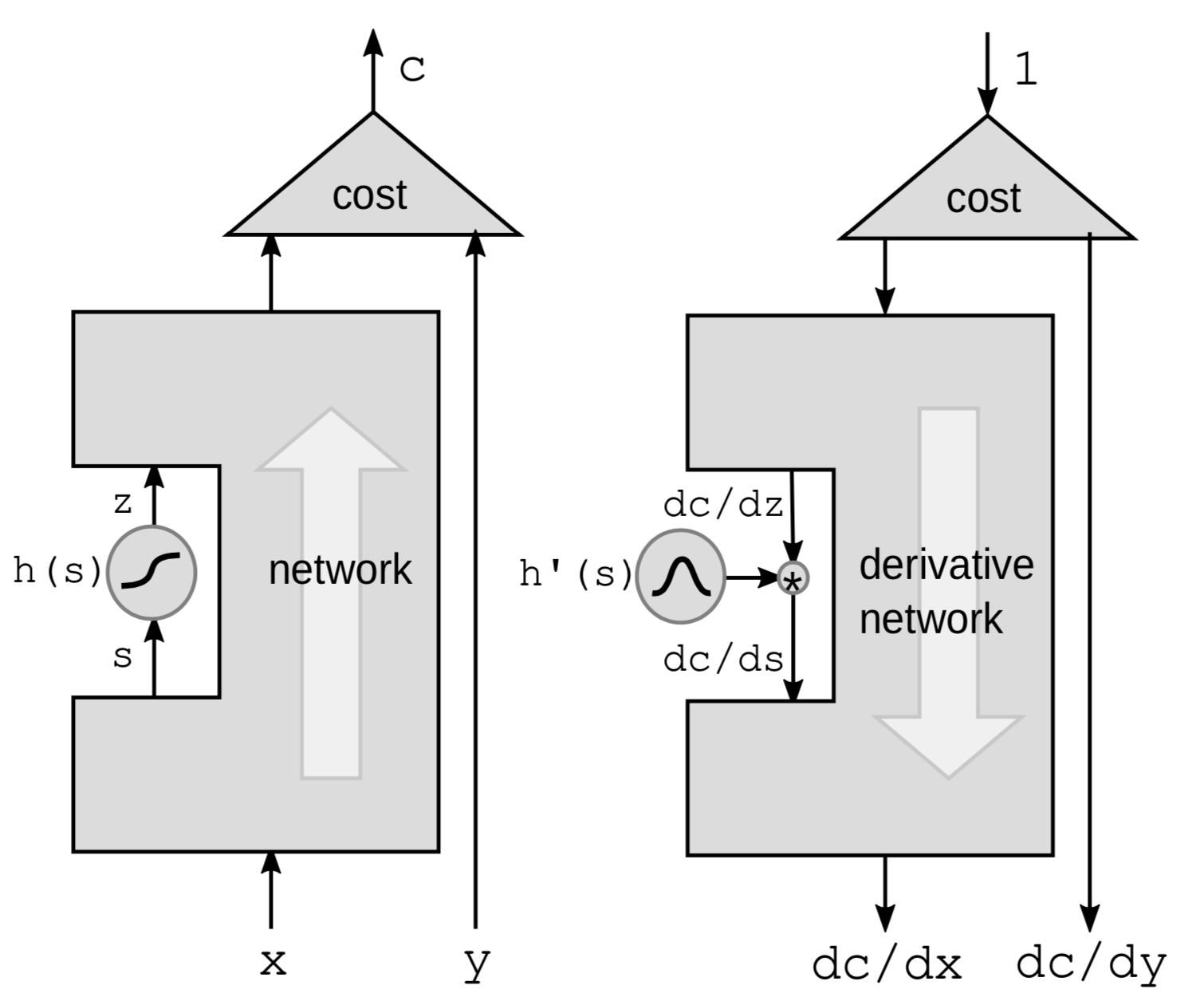Vamos a utilizar la regla de la cadena para calcular los gradientes:

donde $h’(s)$ es la derivada de $z$ con respecto a $s$ representada por $\frac{\mathrm{d}z}{\mathrm{d}s}$. Para hacer clara la conexión entre las derivadas, reescribimos la forma anterior como::

Por tanto, si tenemos una cadena de esas funciones en la red, podemos retropropagar multiplicado por las derivadas de todos las funciones ${h}$ una después de la otra hasta el final.

Es más intuitivo pensar en términos de perturbaciones. Perturbar $s$ en $\mathrm{d}s$ perturbará $z$ en:

Esto a su vez perturbará $C$ en:

De nuevo, terminamos con la misma fórmula que mostramos anteriormente.

Retropropagación a través de una suma ponderada

Para un módulo lineal, hacemos retropropagación a través de una suma ponderada. Acá vemos la red como una caja negra excepto para 3 conexiones que van desde una variable $z$ a un grupo de variables $s$.

Figura 7: Retropropagación a través de una suma ponderada

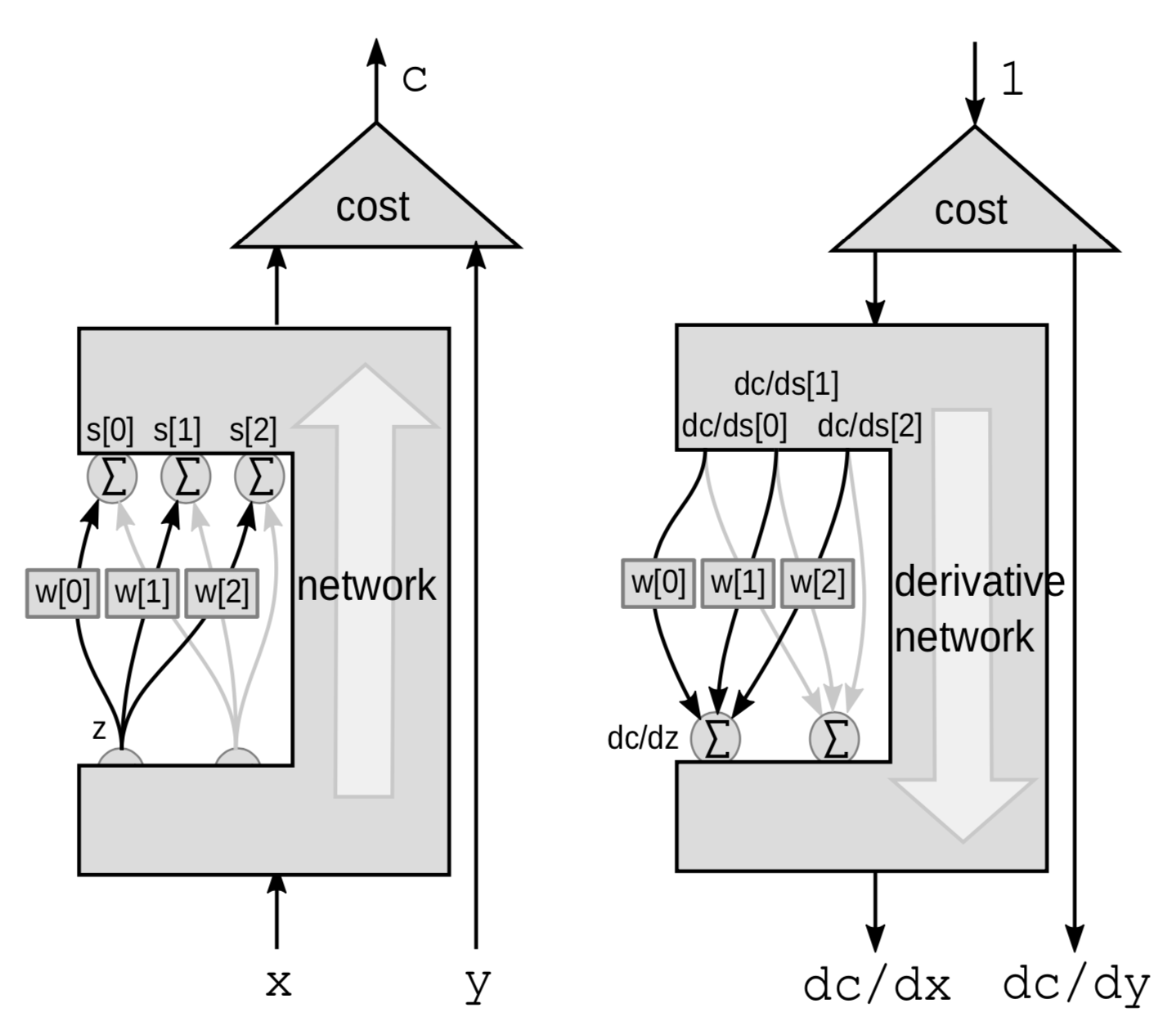Esta vez la perturbación es una suma poderada. $Z$ influye varias variables. Perturbar a $z$ en $\mathrm{d}z$ perturbará $s[0]$, $s[1]$ y $s[2]$ en:

Esto perturbará $C$ en

Por lo tanto, $C$ variará en la suma de las 3 variaciones:

Implementación en Pytorch de la red neuronal y el algoritmo de retropropagación generalizado

Diagrama de bloques de una red neuronal tradicional

• Bloques lineales $s_{k+1}=w_kz_k$

• Bloques no-lineales $z_k=h(s_k)$

  

$w_k$: matriz $z_k$: vector $h$: aplicación de la función escalar $h$ a cada componente. Esta es una red neuronal de 3 capas con pares de funciones lineales y no-lineales, aunque las redes neuronales modernas no tiene claras las separaciones entre lineal y no-lineal y son más complejas.

Implementación en PyTorch

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # flatten input tensor
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

• Podemos implementar redes neuronales con clases orientadas a objetos en PyTorch. Primero, definimos una clase para la red neuronal e inicializamos las capas lineales en el constructor, utilizando la clase predefinida nn.Linear. Las capas lineales tienen que ser objetos separados porque cada una de ellas contiene un vector de parámetros. La clase nn.Linear también agrega el vector de sesgos (bias) implícitamente. Después defininimos una función hacia adelante (forward) de cómo calcular las salidas con la función $\text{torch.relu}$ como la activación no-lineal. No tenemos que inicializar de forma separada las funciones relu porque ellas no tienen parámetros.

• No tenemos que calcular el gradiente nosotros mismos dadro que PyTorch sabe como retropropagar y calcular los gradientes dada la función hacia adelante (forward).

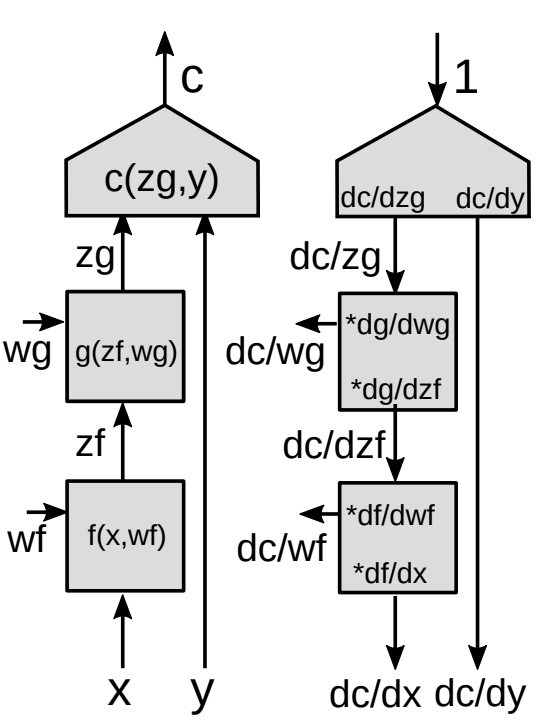
Retropropagación a través de un módulo funcional

Ahora presentamos una forma más generalizada de retropropagación.

Figura 8: Retropropagación a través de un módulo funcional

• Utilizando la regla de la cadena para funciones vectoriales

  \[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

  Esta es la fórmula básica para $\frac{\partial c}{\partial{z_f}}$ utilizando la regla de la cadena. Note que el gradiente de una función escalar con respecto a un vector es un vector del mismo tamaño del vector con respecto al cual se está diferenciando. Con el fin de hacer las notaciones consistentes, es un vector fila en vez de un vector columna.

• Matriz Jacobiana

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

  Necesitamos $\frac{\partial {z_g}}{\partial {z_f}}$ (Entradas de la matriz jacobiana) para calcular el gradiente de la función de costo con respecto a $z_f$ dado el gradiente de la función de costo con respecto a $z_g$. Cada entrada $ij$ es igual a la derivada parcial de la $i-$ésima componente del vector de salida con respecto a la $j-$ésima componente del vector de entrada.

  Si tenemos módulos en cascada, contnuamos multiplicando por la matrices Jacobianas de todos los módulos y obtenemos los gradientes con respecto a todas las variables internas.

Retropropagación a través de una gráfica multi-etapa

Considere un grupo de muchos módulos en una red neuronal como se muestra en la Figura 9.

Figura 9: Retropropagación a través de una gráfica multi-etapa

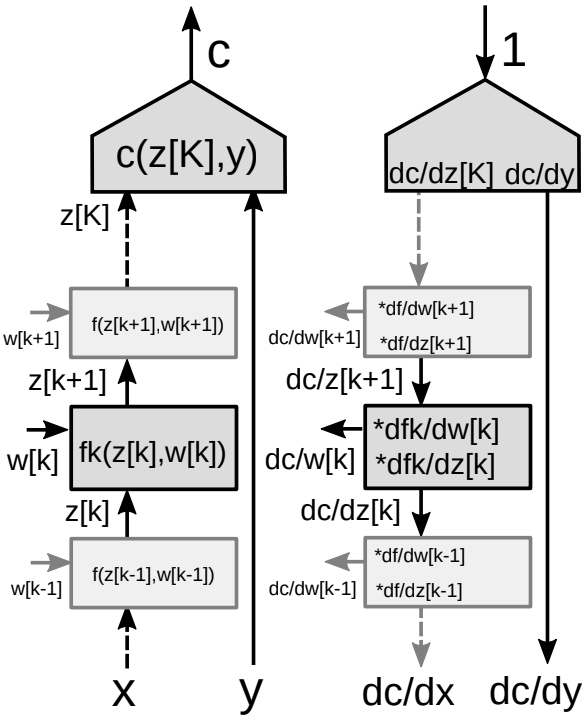Para el algoritmo de retropropagación, necesitamos dos conjuntos de gradientes - uno con respecto a los estados (cada módulo de la red) y uno con respecto a los pesos (todos los parámetros en un módulo particular). Así que tenemos dos matrices Jacobianas asociadas con cada módulo. De nuevo, podemos utilizar la regla de la cadena para hacer reptropropagación.

• Utilizando la regla de la cadena para funciones vectoriales

  \[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• Dos matrices Jacobianas para el módulo

  • Una con respecto a $z[k]$
  • Una con respecto a $w[k]$