Motivación, Álgebra Lineal y Visualización

Recursos

Por favor sigue a Alfredo Canziani en Twitter @alfcnz. Videos y libros con detalles relevantes en álgebra lineal y descomposición en valores singulares (SVD) se pueden encontrar buscando en la cuenta de Twitter de Alfredo, por ejemplo, escribiendo linear algebra (from:alfcnz) en el cuadro de búsqueda.

Transformaciones y motivación

Como ejemplo motivacional, consideremos la clasificación de imágenes. Suponga que tomamos una fotografía con una cámara de 1 mega-píxel. Esta imagen tendrá alrededor de 1000 píxeles verticalmente y 1000 píxeles horizontalmente, y cada píxel tendrá dimensión de tres colores para rojo, verde y azul (RGB). Cada imagen particular puede entonces ser considerada como un punto en un espacio de 3 millones de dimensiones. Con esa amplia dimensionalidad, muchas imágenes interesantes que quisiéramos clasificar – tales como un perro vs. un gato – estarán esencialmente en la misma región del espacio.

Para separar efectivamente estas imágenes, consideramos formas de transformar los datos con el fin de mover los puntos. Recuerde que en un espacio 2-D, una transformación lineal es lo mismo que una multiplicación de matrices. Por ejemplo, las siguientes son transformaciones lineales:

• Rotación (cuando la matriz es ortonormal).
• Escalamiento (cuando la matriz es diagonal).
• Reflexión (cuando el determinante es negativo).
• Cizallamiento o Transvección (Shear)

Observa que la traslación por si sola no es lineal dado que 0 no siempre será mapeado a 0, sin embargo es una transformación afín. Volviendo a nuestro ejemplo en imágenes, podemos transformar los puntos trasladándolos de forma tal que sean agrupados alrededor de 0 y escalados con una matriz diagonal de tal forma que nos acerquemos a esa región. Finalmente, podemos hacer clasificación hallando lineas a través del espacio que separen los diferentes puntos en sus respectivas clases. En otras palabras, la idea es usar transformaciones lineales y no lineales para mapear los puntos a un espacio donde sean linealmente separables. Esta idea se hará más concreta en las siguientes secciones.

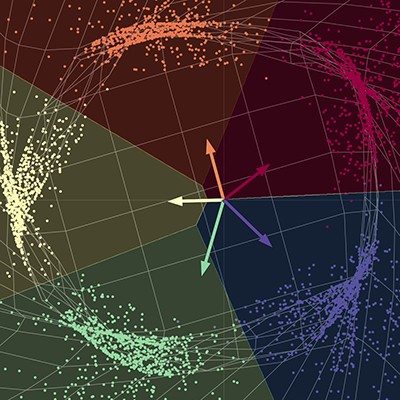
Visualización de datos - separando puntos por colores utilizando una red

En nuestra visualización, tenemos cinco ramas de una espiral, cada rama corresponde a un color diferente. Los puntos viven en un plano bidimensional y pueden ser representados como una tupla; el color representa una tercera dimensión que puede ser pensada como la clase para cada uno de los puntos. Entonces utilizamos la red para separar cada uno de los puntos por color.

(a) Puntos de entrada - antes de la red	(b) Puntos de salida - después de la red

La red “comprime” el espacio fabricado con el fin de separar cada uno de los puntos en diferentes subespacios. Cuando converge, la red separa cada uno de los colores en cuatro diferentes subespacios de la variedad final. En otras palabras, cada uno de los colores en este nuevo espacio será linealmente separable utilizando una regresión del tipo una vs todas. Los vectores en el diagrama pueden ser representados como una matriz de 5 por 2; esta matriz puede ser multiplicada con cada punto para devolver puntuaciones para cada uno de los cinco colores. Cada uno de los puntos se puede entonces clasificar por color utilizando sus respectivas puntuaciones. Aquí, la dimensión de salida es cinco, una para cada uno de los colores, y la dimensión de entrada es dos, una para las coordenadas x e y de cada uno de los puntos. Para resumir, esta red básicamente comprime el espacio fabricado y realiza una transformación parametrizada por varias matrices y por no-linealidades.

Arquitectura de la red

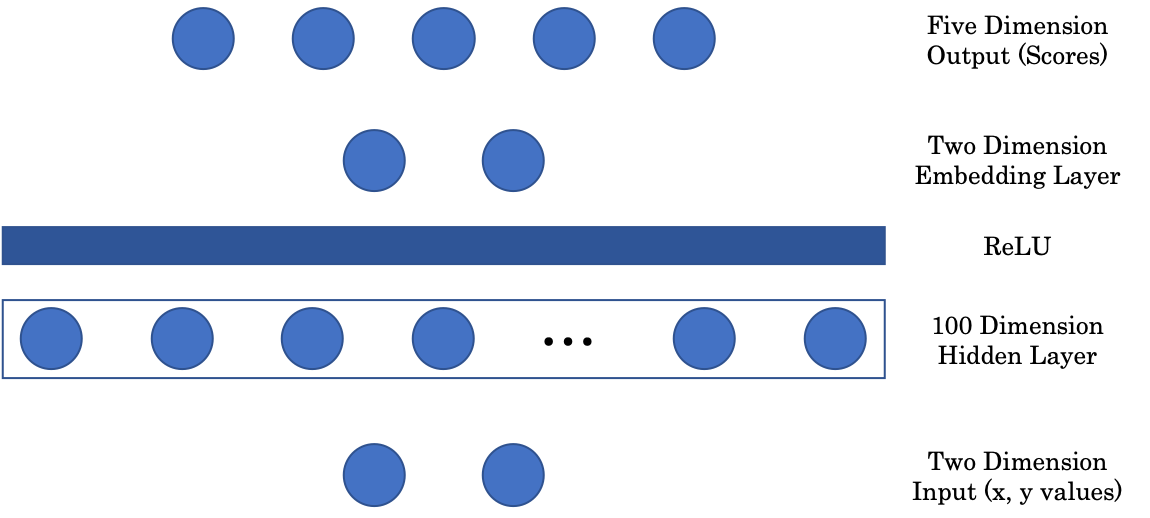
Figura 2: Arquitectura de la red

La primera matriz mapea la entrada bidimensional a una capa oculta intermedia de 100 dimensiones. Después tenemos una capa no-lineal, ReLU o Unidad Lineal Rectificada, que es simplemente la función parte positiva $(\cdot)^+$. Después, para mostrar nuestra imagen en una representación gráfica, incluimos una capa de tipo embedding que mapea la capa oculta de entrada 100 dimensional a una salida bidimensional. Finalmente, la capa de embedding se proyecta a la capa final de 5 dimensiones de la red, representando una puntuación para cada color.

Proyecciones aleatorias - Jupyter Notebook

El documento Jupyter Notebook se puede encontrar aquí. Para ejecutarlo, asegúrate de tener el ambiente pDL instalado como se especifica en README.md.

PyTorch device

PyTorch se puede ejecutar tanto en la CPU como en la GPU del computador. La CPU es útil para tareas secuenciales, mientras que la GPU es útil para tareas en paralelo. Antes de ejecutar en el dispositivo seleccionado, debemos primero asegurarnos de que nuestros tensores y modelos se transfieran a la memoria del dispositivo. Esto se puede hacer con las siguientes dos líneas de código:

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)

La primera línea crea una variable, llamada device (dispositivo), que se asigna a la GPU si está disponible; de otra forma, se asigna por defecto a la CPU. En la siguiente linea, se crea un tensor y se envía a la memoria del dispositivo llamando .to(device).

Jupyter Notebook tip

Para ver la documentación para una función en una celda del notebook, utilice Shift + Tab.

Visualizando transformaciones lineales

Recuerde que una transformación lineal se puede representar como una matriz. Utilizando descomposición en valores singulares, podemos descomponer esta matriz en tres matrices de componentes, cada una representando una transformación lineal diferente.

En la eq.(1), las matrices $U$ y $V^\top$ son ortogonales y representan las transformaciones rotación y reflexión. La matriz del medio es diagonal y representa una transformación de escalamiento.

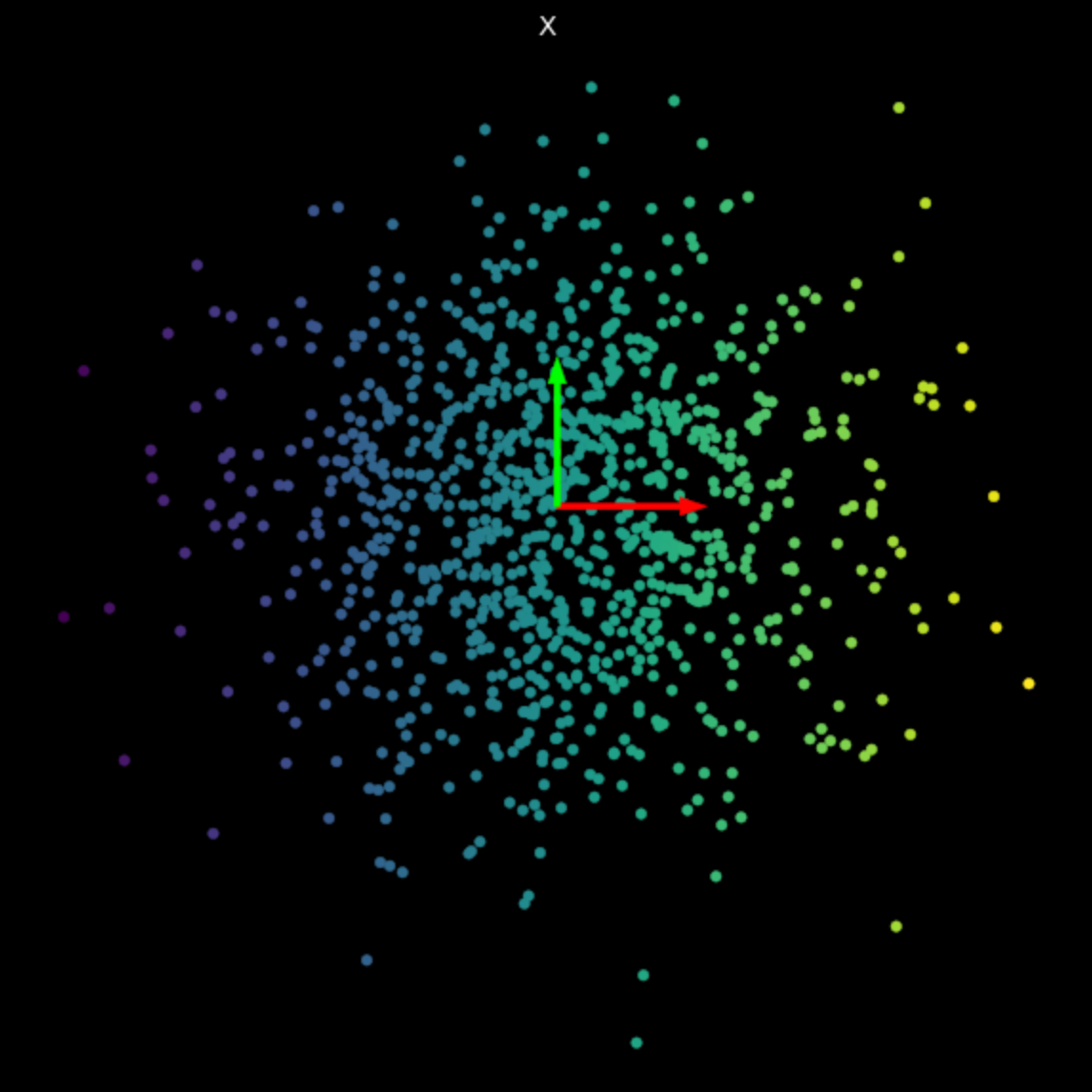
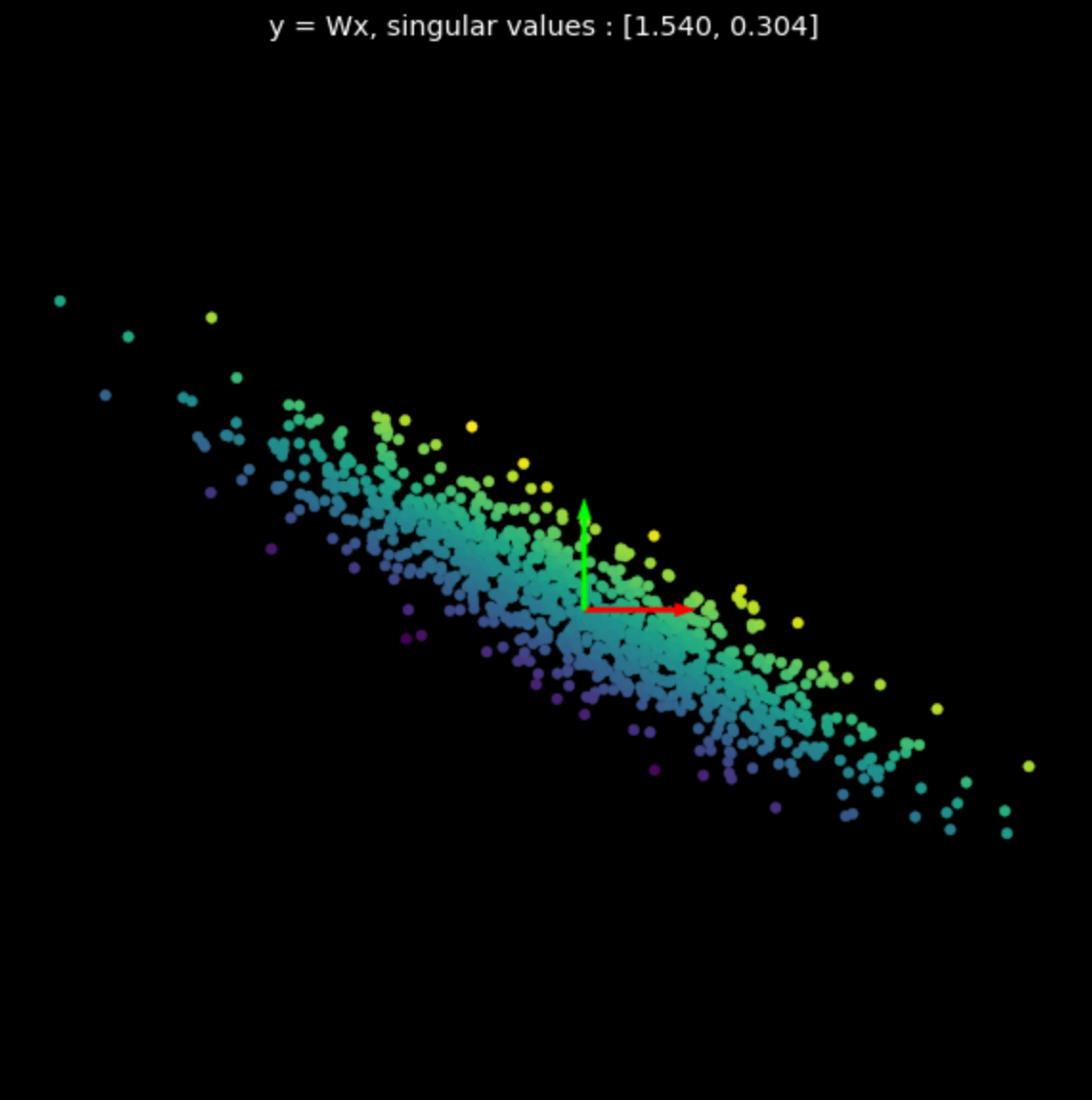
Visualizamos la transformación lineal de varias matrices aleatorias en la Fig.3. Note el efecto de los valores singulares en las transformaciones resultantes.

Las matrices utilizadas se generaron con Numpy; sin embargo, podemos utilizar también la clase de Pytorch nn.Linear con bias = False para crear transformaciones lineales.

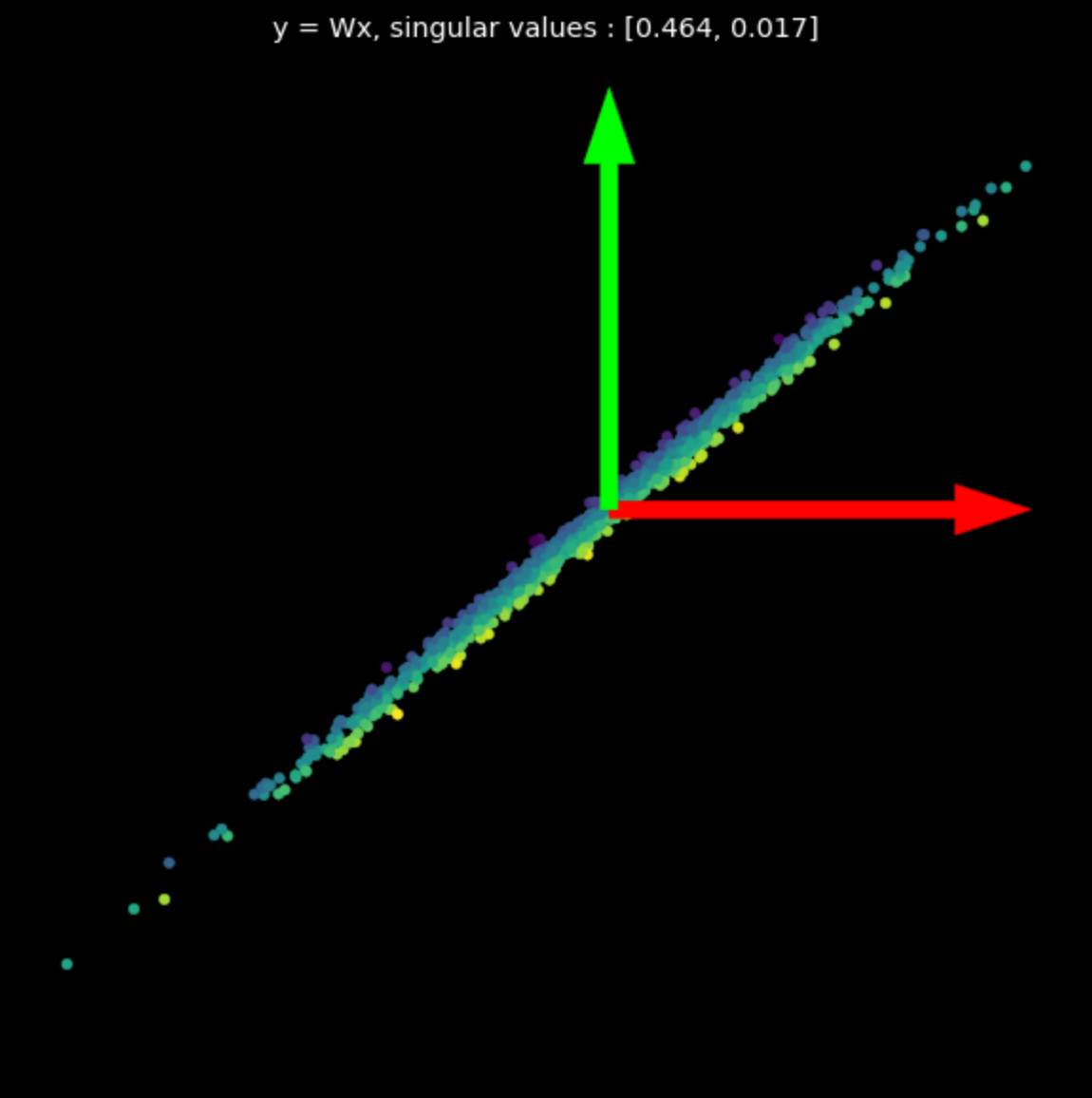(a) Puntos originales	(b) $s_1$ = 1.540, $s_2$ = 0.304	(c) $s_1$ = 0.464, $s_2$ = 0.017

Transformaciones no-lineales

A continuación, visualizamos la siguiente transformación:

Recuerda, la gráfica de $\tanh(\cdot)$ en Fig. 4.

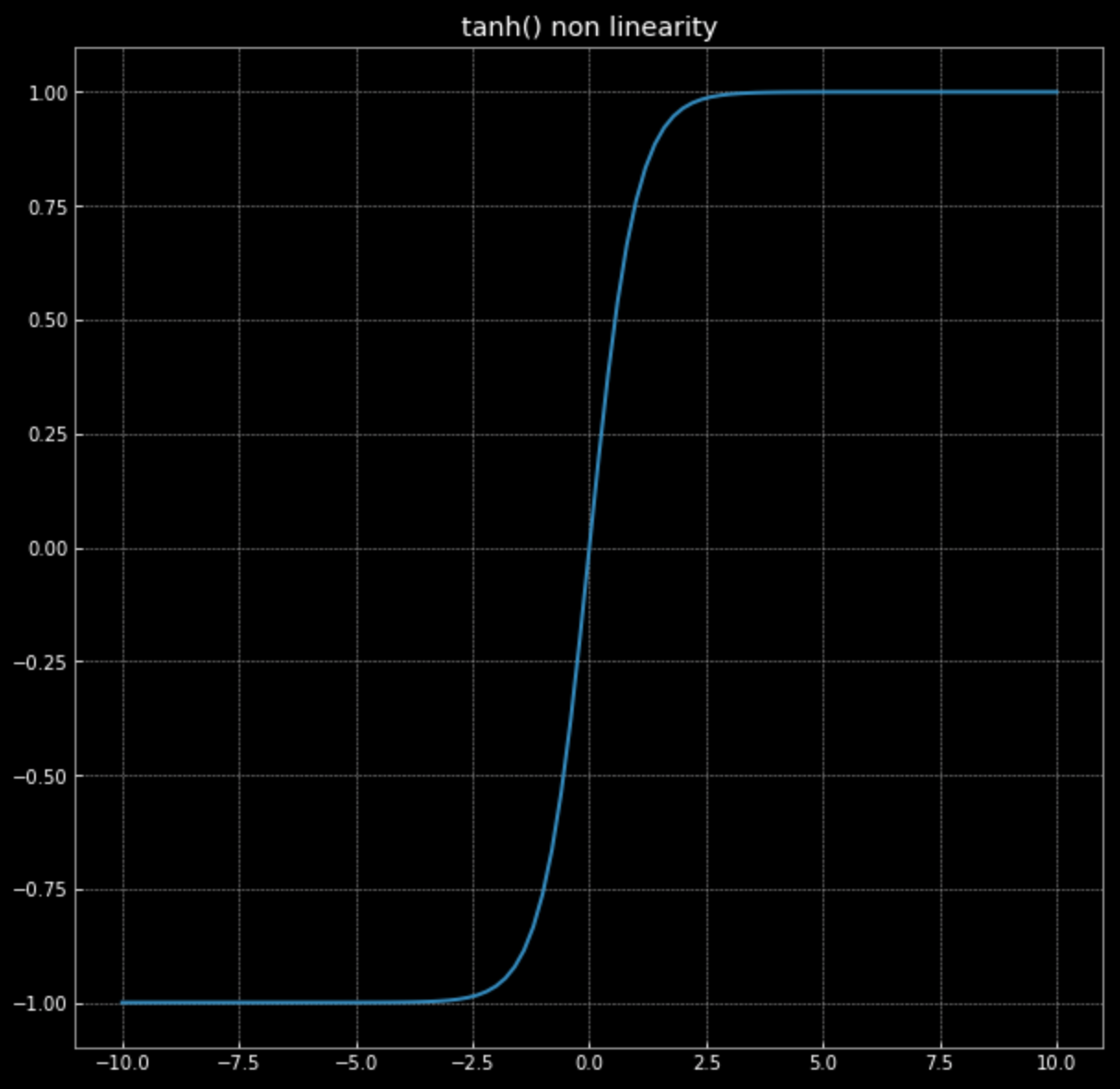
Figura 4: No-linealidad tangente hiperbólica

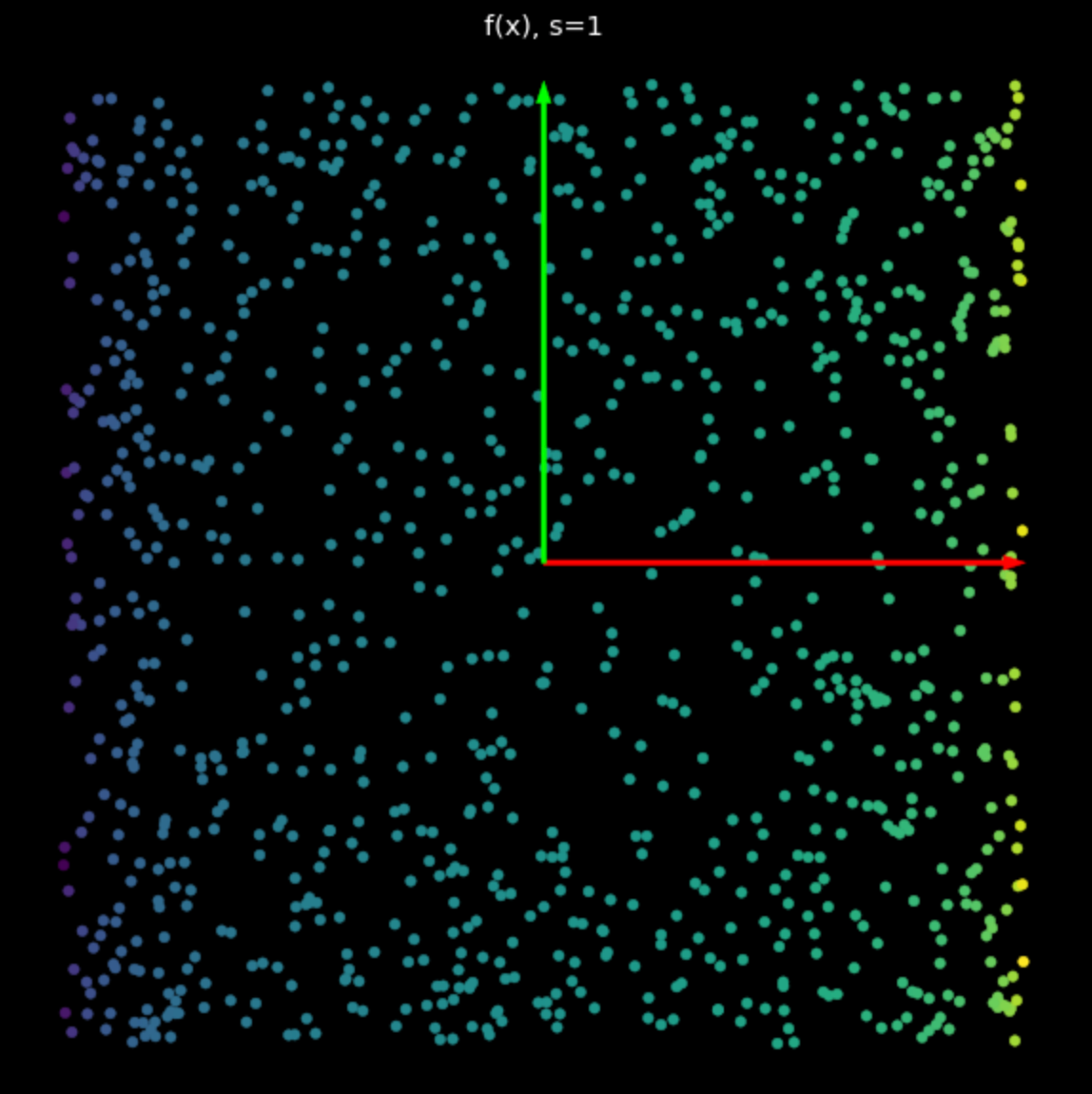
El efecto de esta no-linealidad es acotar puntos entre $-1$ y $+1$, creando un cuadrado. A medida que el valor de $s$ en eq. (2) aumenta, más y más puntos se empujan al borde del cuadrado. Esto se muestra en Fig. 5. Llevando más puntos a la esquina, los separamos más y podemos entonces intentar clasificarlos.

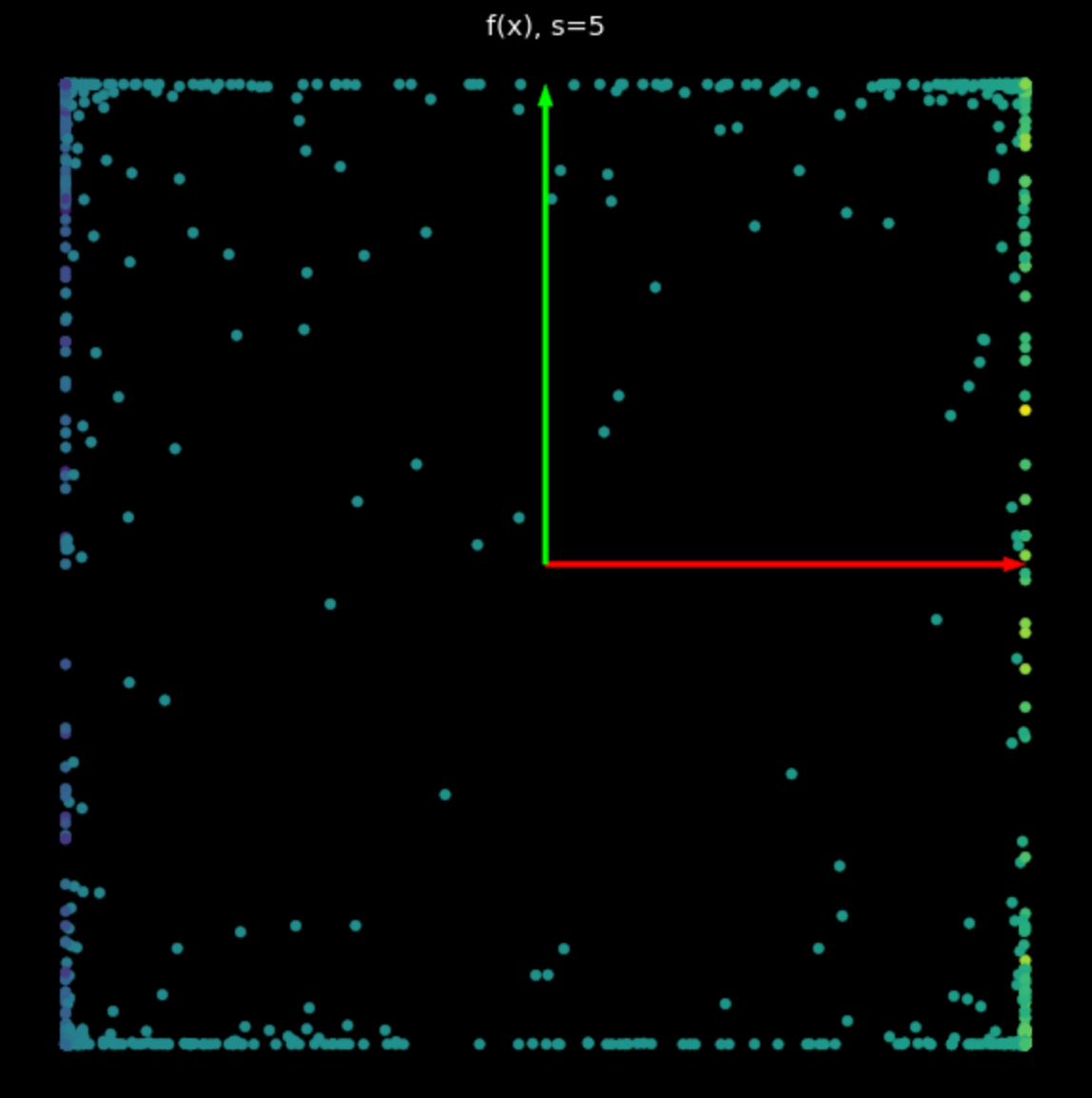(a) No-linealidad con $s=1$	(b) No-linealidad con $s=5$

Red neuronal aleatoria

Finalmente, visualizamos la transformación realizada por una simple red neuronal sin entrenar. La red consiste de una capa lineal, que realiza una transformación afín, seguida por una no-linealidad tangente hiperbólica, y finalmente otra capa lineal. Examinando la transformación en la Fig. 6, observamos que es poco probable que veamos las transformaciones lineales y no-lineales de antes. Avanzando, veremos cómo hacer que estas transformaciones realizadas por las redes neuronales sean útiles para nuestro objetivo final de clasificación.

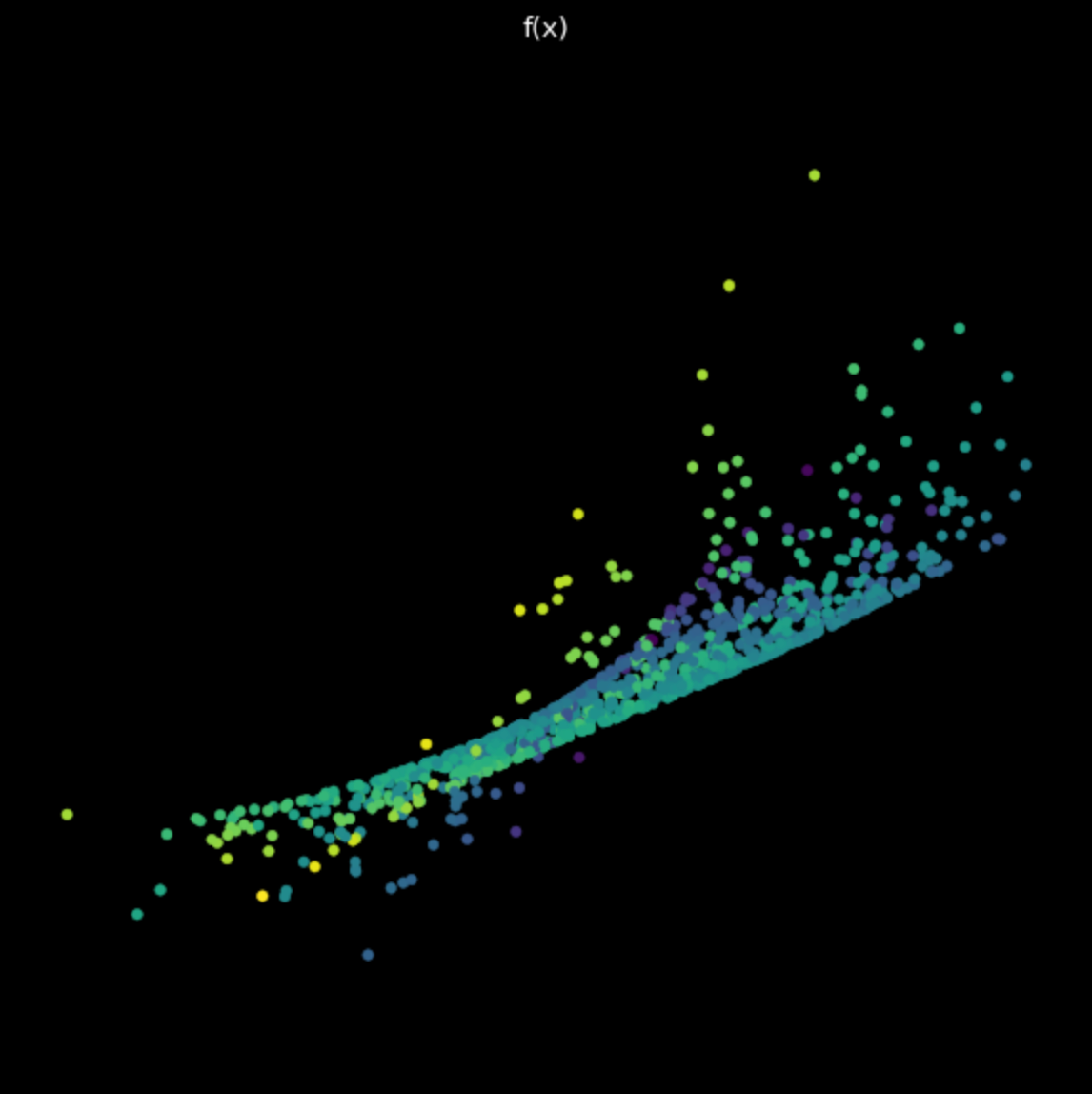
Figura 6: Transformación de una red neuronal sin entrenar