أساليب الرسم البياني المبنية على الطاقة
🎙️ Yann LeCunمقارنة الخسائر (Losses)
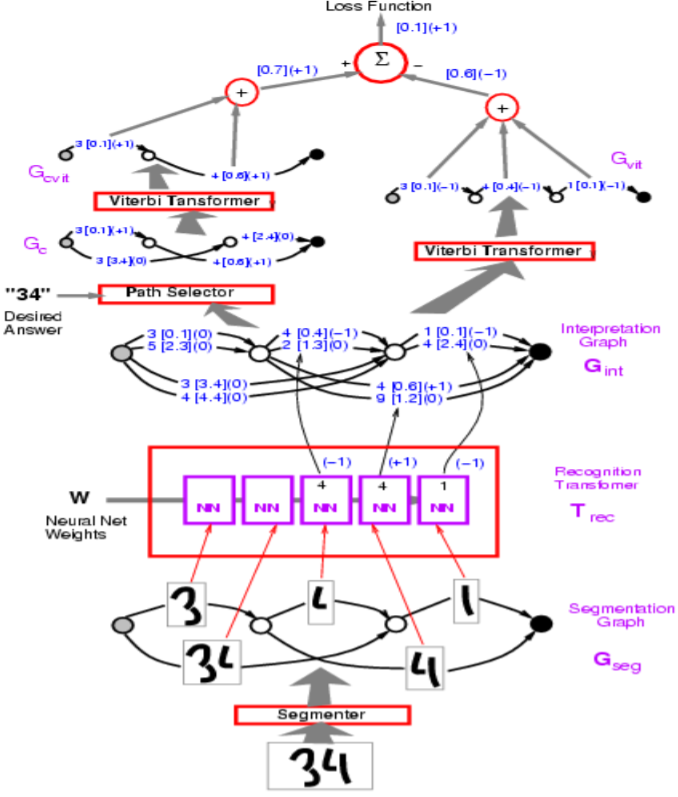
الشكل 1: هيكل الشبكة
في الشكل أعلاه، تحتوي المسارات غير الصحيحة على -1.
يبدأ البروفيسور LeCun بفقدان الإدراك الحسي، والذي يستخدم في مثال نموذج محول الرسم البياني في الشكل أعلاه. الهدف هو جعل الطاقة من الإجابات الخاطئة كبيرة، والإجابات الصحيحة صغيرة.
من حيث التنفيذ، يمكنك تمثيل الأقواس في التصور باستخدام متجه (vector). بدلاً من استخدام قوس منفصل لكل فئة، يمكننا استعمال متجه واحد يحتوي على كل من الفئات والنتيجة لكل فئة.
س: كيف يتم تنفيذ المقسم (segmentor) في النموذج أعلاه؟
ج: الجزء هو التنبؤ اليدوي(handcrafted heuristics) . يستخدم النموذج مقسمًا يدويًا على الرغم من وجود طريقة لجعله قابلاً للتدريب من طرف إلى طرف (end-to-end). تم استبدال هذا النهج بنهج النافذة المنزلقة للتعرف على الأحرف أو ما يعرف بالإنجليزية the sliding window.
نظرة عامة على الخسائر
| Ecuacion de pérdida | Formula | Margen |
|---|---|---|
| Perdida de energia | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)$ | None |
| Perceptron | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)-\min\limits_{\text{Y}\in\mathcal{Y}}\text{E}(\text{W}, \text{Y}, \text{X}^i)$ | 0 |
| Bisagra | $\max\big(0, m + \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | $m$ |
| Log | $\log\bigg(1+\exp\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | >0 |
| LVQ2 | $\min\bigg(M, \max\big(0, \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | 0 |
| MCE | $\bigg(1+\exp\Big(-\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\Big)\bigg)^{-1}$ | >0 |
| Cuadrado-cuadrado | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2-\bigg(\max\big(0, m - \text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)^2$ | $m$ |
| Cuadrado-Exp | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2 + \beta\exp\big(-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | >0 |
| NNL/MMI | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i) + \frac{1}{\beta}\log\int_{y\in\mathcal{Y}}\exp\big(-\beta\text{E}(\text{W}, y,\text{X}^i)\big)$ | >0 |
| MEE | $1-\frac{\exp\big(-\beta E(W,Y^i,X^i)\big)}{\int_{y\in\mathcal{Y}}\exp\big(-\beta E(W,y,X^i)\big)}$ | >0 |
إن خسارة الإدراك الحسي (percepton loss) كما في الجدول أعلاه ليس لها هامش، وبالتالي فإن الخسارة تنطوي على خطر الانهيار.
- فقدان المفصلة (hinge) هو أخذ طاقة الإجابة الأكثر ضررًا، والإجابة الصحيحة، وحساب الفرق بينهما. حدسيًا، مع وجود هامش م، ستفقد المفصلة 0 فقط عندما تكون الطاقة الصحيحة أقل من الطاقة الأكثر ضررًا بمقدار _ على الأقل _ م.
-
يُستخدم فقدان MCE في التعرف على الكلام، ويبدو مشابهًا للدالة السينية (sigmoid).
- يهدف فقدان NLL إلى جعل طاقة الإجابة الصحيحة صغيرة، وجعل جزء log في المعادلة كبيرًا.
س: كيف يمكن أن تكون المفصلة (hinge) أفضل من خسارة NLL؟
ج: المفصلة (hinge) أفضل من NLL لأن NLL ستحاول دفع الفرق بين الإجابة الصحيحة والإجابات الأخرى إلى ما لا نهاية، في حين أن المفصلة تريد فقط جعلها أكبر من بعض القيم (الهامش م.)
تعريف:
يقوم مفكك الشفرة (decoder) بإدخال سلسلة من المتجهات التي تشير إلى درجات أو طاقة الأصوات أو الصور، وتختار أفضل إخراج ممكن.
س: ما هي بعض الأمثلة على المشاكل التي يمكن أن تستخدم مفككي التشفير (decoders)؟ ج: نمذجة اللغة والترجمة الآلية وعلامات التسلسل.
خوارزمية forward في شبكات محول الرسم البياني
تكوين الرسم البياني
يسمح لنا تكوين الرسم البياني بدمج رسمين بيانيين. في هذا المثال، يمكننا أن نرى معجم نموذج اللغة يتم تمثيله على شكل $ trie $ (رسم بياني) ورسم بياني للتعرف يتم إنتاجه بواسطة شبكة عصبية.
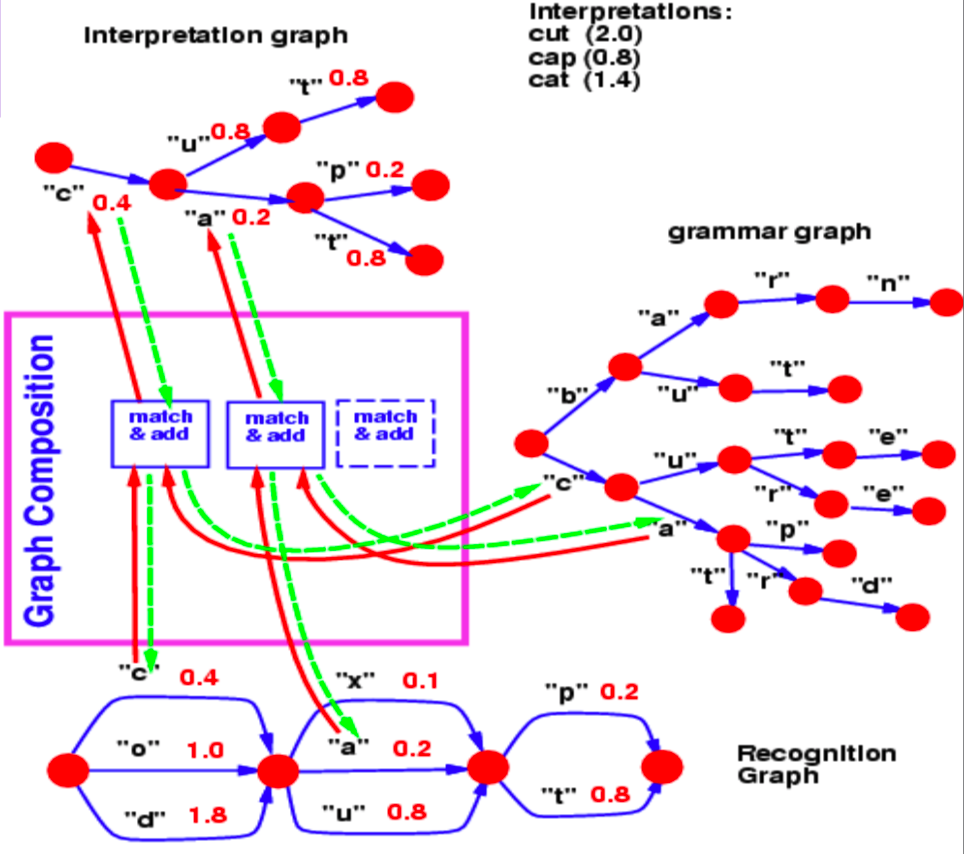
الشكل 2:: تكوين الرسم البياني
يحدد رسم التعرف البياني بقيم طاقة مختلفة (مرتبطة بكل قوس) مدى احتمالية وجود حرف في خطوة معينة.
الآن، في هذا المثال، السؤال الذي نجيب عليه من خلال عملية تكوين الرسم البياني هو، ما هو أفضل مسار في مخطط التعرف هذا الذي يتوافق أيضًا مع قاموسنا؟
القفزة الشائعة من الخطوة 1 إلى الخطوة 2 بين الرسم التعرف البياني هي الحرف $c$، المرتبط بالطاقة 0.4. وبالتالي، فإن الرسم البياني الخاص بنا يحتوي على قوس واحد فقط بين الخطوتين 1 و 2 المقابل لـ $c$. وبالمثل، فإن الأحرف المحتملة بين الخطوتين 2 و 3 هي $x$ و $u$ و $a$ في رسم التعرف البياني. تحتوي الفروع التي تلي $c$ في الرسم البياني النحوي على $u$ و $a$. لذلك، تختار عملية تكوين الرسم البياني الأقواس $u$ و $a$ لتواجدهما في الرسم البياني للتفسير. كما أنه يربط القوس الذي ينسخه من رسم التعرف البياني بقيم الطاقة.
إذا احتوت القواعد النحوية أيضًا على قيم طاقة مرتبطة بالأقواس، فإن تكوين الرسم البياني كان سيضيف قيم الطاقة أو يجمعها باستخدام عامل آخر (operator).
بطريقة مماثلة ، يسمح لنا تكوين الرسم البياني أيضًا بدمج قاعدتين معرفيتين يتم تمثيلهما بواسطة الشبكات العصبية. في المثال السابق، يمكن تمثيل القواعد بشكل أساسي كشبكة عصبية تتنبأ بالحرف التالي. يوفر لنا ناتج softmax الخاص بالشبكات العصبية احتمالات الانتقال إلى الحرف التالي من عقدة معينة.
كملاحظة جانبية، إذا كان نموذج اللغة الموضح في هذا المثال عبارة عن شبكة عصبية، فيمكننا إعادة الانتشار عبر البنية بأكملها. يصبح هذا مثالًا لبرنامج مختلف حيث نقوم بإعادة النشر من خلال برنامج يحتوي على حلقات، شروط، تكرارية، إلخ.
قارئ الشيكات من منتصف التسعينيات
تعتبر البنية الكاملة لقارئ الشيكات من منتصف التسعينيات معقدة للغاية، ولكن ما يهمنا في المقام الأول هو الجزء الذي يبدأ من أداة التعرف على الأحرف، والتي تنتج الرسم البياني للتعرف.
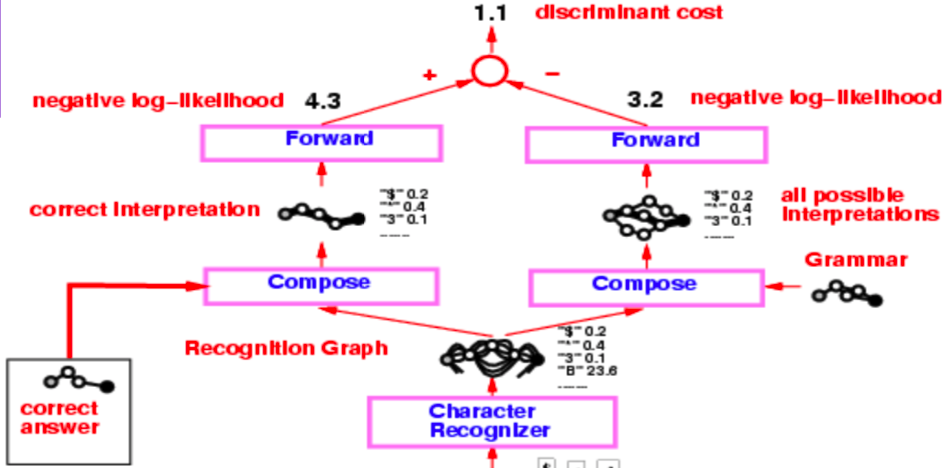
الشكل #: قارئ الشيكات
يخضع الرسم البياني للتعرف على عمليتي تكوين منفصلتين، إحداهما مع التفسير الصحيح (أو الحقيقة الأساسية) والثانية مع القواعد النحوية التي تنشئ رسمًا بيانيًا لجميع التفسيرات الممكنة.
يتم تدريب النظام بأكمله عبر دالة الأرجحية اللوغارثمية السلبية (Negative Log-Likelihood). تبين هذه الدالة أن كل مسار في الرسم البياني للتفسير هو تفسير محتمل ومجموع الطاقات على طول هذا المسار هو طاقة ذلك التفسير.
الآن، بدلاً من استخدام خوارزمية Viterbi، نستخدم خوارزمية forward (forward algorithm). تناقش الأقسام الفرعية التالية الاختلافات بين النهجين.
Viterbi خوارزمية
خوارزمية Viterbi هي خوارزمية برمجة ديناميكية تُستخدم للعثور على المسار الأكثر احتمالًا (أو المسار مع الحد الأدنى من الطاقة) في رسم بياني معين. إنه يقلل الطاقة فيما يتعلق بالمتغير الكامن z، حيث يمثل z المسار الذي نسلكه في الرسم البياني.
\[F (x, y) = \min_{z} \; E(x, y, z)\]خوارزمية forward
من ناحية أخرى، تقوم الخوارزمية الأمامية بحساب اللوغاريثم للمجموع الأسي للقيمة السالبة لطاقات جميع المسارات. يمكن رؤية هذا الفم بسهولة كصيغة أدناه:
\[F_{\beta} (x, y) = -\frac{1}{\beta} \; \log \; \sum_{z \, \in \, \text{paths}} \; \exp \, (- \beta \; E(x, y, z))\]هذا هو التهميش على المتغير الكامن z، الذي يحدد المسارات في الرسم البياني التفسير. يحسب هذا الأسلوب القيمة الأسية لمجموع اللوغاريثم هذا على جميع المسارات الممكنة لعقدة معينة. هذا يشبه تمشيط تكلفة جميع المسارات الممكنة بأدنى حد ممكن.
خوارزمية forward هي خوارزمية سهلة التنفيذ ولا تكلف أكثر من خوارزمية Viterbi. أيضًا، يمكننا أن نستعمل الانتشار الخلفي من خلال عقدة الخوارزمية الأمامية في الرسم البياني.
يمكن عرض عمل خوارزمية forward باستخدام المثال التالي المحدد في رسم بياني للتفسير.
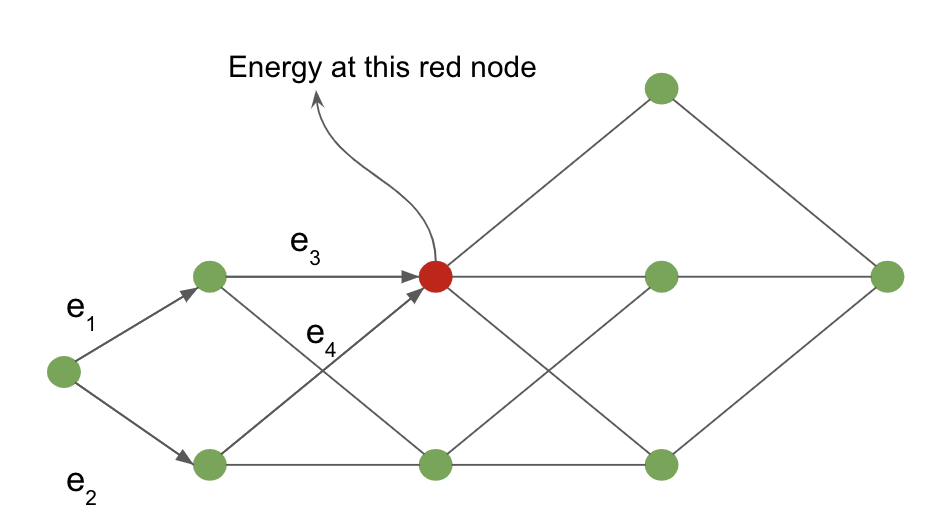
الشكل 4 : الرسم التفسيري البياني
يتم حساب التكلفة من عقدة الإدخال إلى العقدة المظللة باللون الأحمر عن طريق التهميش على جميع المسارات الممكنة التي تصل إلى العقدة الحمراء. تحدد الأسهم التي تدخل العقدة الحمراء هذه المسارات المحتملة في مثالنا.
بالنسبة للعقدة الحمراء، تُعطى قيمة الطاقة في العقدة من خلال:
\[-\frac{1}{\beta} \; \log \; [ \, \exp \, (- \, \beta (e_1 \, + \, e_3)) \; + \; \exp \, (- \, \beta (e_2 \, + \, e_4)) \, ]\]تشبيه الشبكة العصبية لخوارزمية forward
تعد خوارزمية forward حالة خاصة لخوارزمية انتشار المعتقد (belief-propagation algorithm)، عندما يكون الرسم البياني الأساسي عبارة عن رسم بياني متسلسل. يمكن النظر إلى هذه الخوارزمية بأكملها على أنها شبكة عصبية تلقائية للأمام حيث تكون الوظيفة في كل عقدة عبارة عن مجموع اللوغاريثم الأسي بإضافة ثابت.
لكل عقدة في الرسم البياني التفسير، نحافظ على متغير $\alpha$.
\[\alpha_{i} = - \; \log \; \biggl[ \sum_{k \, \in \, \text{parent} \, (i)} \; \exp \, (- \, \beta \; (\alpha_k \, + \, e_{ki})) \biggl]\]حيث $e_{ki}$ هي طاقة الارتباط من العقدة $k$ إلى العقدة $i$.
يشكل $\alpha_i$ تنشيط العقدة $i$ في هذه الشبكة العصبية و $e_{ki}$ هو الوزن بين العقد $k$ والعقدة $i$. هذه الصيغة مكافئة جبريًا لعمليات المجموع الموزون لشبكة عصبية عادية في مجال log.
يمكننا النسخ العكسي من خلال الرسم البياني للتفسير الديناميكي (لأنه يتغير من مثال إلى مثال) الذي نطبق عليه خوارزمية forward. يمكننا حساب تدرجات $F(x, y)$ المحسوبة في العقدة الأخيرة من الرسم البياني بالنسبة إلى أوزان $e_{ki}$ التي تحدد حواف الرسم البياني للتفسير.

الشكل 5: قارئ الشيكات
بالعودة إلى مثال قارئ الشيك، نطبق خوارمية forward على تكوينات الرسم البياني ونحصل على قيمة الطاقة في العقدة الأخيرة باستخدام مجموع اللوغاريثم الأسي log sum exponential. الفرق بين قيم الطاقة هذه هو مقدار خسارة الأرجحية اللوغاريثمية السلبية (negative log-likelihood loss).
القيمة التي تم الحصول عليها من تطبيق خوارزمية forward على تكوين الرسم البياني بين الإجابة الصحيحة ورسم التعرف على البيانات هي القيمة الأسية لمجموع اللوغاريثم log sum exponential للإجابة الصحيحة. في المقابل، فإن القيمة الأسية لمجموع اللوغاريثم في العقدة الأخيرة لتكوين الرسم البياني بين الرسم البياني للتعرف والقواعد هي القيمة المهمشة على جميع التفسيرات الصحيحة الممكنة.
صيغة لاغرانج للانتشار الخلفي
بالنسبة للإدخال $x$ والمخرج المستهدف $y$، يمكننا صياغة شبكة كمجموعة من الوظائف، $f_k$ والأوزان، $w_k$ مثل تلك الخطوات المتعاقبة في إخراج الشبكة $z_k$ مع $z_{k+1} = f_k(z_k, w_k)$. في الإعداد الخاضع للإشراف، يتمثل هدف الشبكة في تقليل $C(z_n, y)$، وهي تكلفة ناتج الشبكة رقم $n$، فيما يتعلق بالحقيقة الأساسية. هذا يعادل مشكلة تصغير $C(z_n, y)$ فيما يتعلق بالقيود $z_{k+1} = f_k(z_k, w_k)$ و $z_0 = x$.
يمكن كتابة اللاغرانج: \(\mathcal{L}(x, y, \lambda_i, z_i, w_i) = C(z_n, y) + \sum\limits_{k=0}^{n-1} \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k))\) حيث تشير مصطلحات $ \lambda $ إلى مضاعفات لاجرانج (راجع ملاحظات بول عبر الإنترنت لتجديد المعلومات إذا كان الحساب 3 منذ فترة)
لتقليل $\mathcal{L}$، نحتاج إلى تعيين المشتقات الجزئية لـ $\mathcal{L}$ بالنسبة لكل من عناصرها إلى الصفر وحلها.
- بالنسبة إلى $\lambda$، نستعيد القيد : $\frac{\partial{\mathcal{L}}}{\partial \lambda_{k+1}} = 0 \rightarrow z_{k+1} = f_k(z_k, w_k)$.
- بالنسبة إلى $z_k$، $\frac{\partial \mathcal{L}}{\partial z_k} = 0 \rightarrow \lambda^T_k - \lambda^T_{k+1} \frac{\partial f_k(z_k, w)}{\partial z_k} \rightarrow \lambda_k = \frac{\partial f_k(z_k, w_k)^T}{\partial z_k}\lambda_{k+1}$, وهي مجرد صيغة الانتشار الخلفي القياسية.
نشأ هذا النهج مع لاغرانج وهاملتون في سياق الميكانيكا الكلاسيكية، حيث يكون التقليل على طاقة النظام بينما يشير مصطلح $ \ lambda $ إلى القيود المادية للنظام، مثل إجبار كرتين على البقاء على مسافة ثابتة عن بعضها البعض بحكم ربطها بقضيب معدني، على سبيل المثال.
في الحالة التي نحتاج فيها إلى تقليل التكلفة $C$ في كل خطوة زمنية، $k$، يصبح Lagrangian \(\mathcal{L} = \sum_k \left(C_k(z_k, y_k) + \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k)) \right)\).
المعادلة التفاضلية العصبية العادية (ODE)
باستخدام هذه الصيغة من الانتشار الخلفي، يمكننا الآن التحدث عن فئة جديدة من النماذج، Neural ODEs. هذه شبكات متكررة بشكل أساسي حيث يتم إعطاء الحالة $z$ في الوقت $ t $ بواسطة $ z_{t+\text{d}t} = z_t + f(z_t, W) dt $، حيث يمثل $W$ مجموعة من المعاملات الثابتة. يمكن أيضًا التعبير عن ذلك في صورة معادلة تفاضلية عادية (بدون مشتقات جزئية): $\frac{\text{d}z}{\text{d}t} = f(z_t, W)$.
يعد تدريب مثل هذه الشبكة باستخدام صيغة لاغرانج أمرًا سهلاً للغاية. إذا كان لدينا هدف، $y$، ونريد أن تصل حالة النظام إلى $y$ بمرور الوقت $T$، فإننا ببساطة نؤسس دالة التكلفة على أنها المسافة بين $z_T$ و $y$. يمكن أن يكون الهدف الآخر للشبكة هو العثور على حالة مستقرة للنظام، أي حالة تتوقف عن التغيير بعد نقطة معينة. رياضيا، هذا يعادل إعداد $\frac{\text{d}z}{\text{d}t} = f(y, W) = 0$. بشكل عام، العثور على حل، $y$ لهذه المعادلة أسهل بكثير من الانتشار العكسي عبر الزمن، لأن الشبكة لا تحتاج إلى تذكر التدرج اللوني فيما يتعلق بالتسلسل بأكمله، وعليها فقط تقليل $f$ أو $\lvert f \rvert^2$. لمزيد من المعلومات حول تدريب ODE العصبي للوصول إلى النقاط الثابتة، راجع [(Lecun88)] (http://yann.lecun.com/exdb/publis/pdf/lecun-88.pdf).
التبنؤ المتغير من حيث الطاقة
مقدمة
بالنسبة لدالة الطاقة الأولية $E(x,y,z)$، إذا أردنا التهميش على متغير، z، للحصول على خسارة من حيث $x$ و $y$، $L(x,y)$، يجب أن نحسب \(L(x,y) = -\frac{1}{\beta}\int_z \exp(-\beta E(x,y,z))\) إذا ضربنا بعد ذلك في $ \ frac {q (z)} {q (z)} $، فسنحصل على \(L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\) إذا افترضنا أن $ q (z) $ هو توزيع احتمالي يزيد عن $z$، فيمكننا تفسير دالة الخسارة المعاد كتابتها باعتبارها قيمة متوقعة، فيما يتعلق بتوزيع $\frac{\exp({-\beta E(x,y,z)})}{q(z)}$. نحن نستخدم هذا التفسير، تباين جنسن (Jensen’s Inequality)، والتقريب القائم على أخذ العينات، لتحسين وظيفة الخسارة لدينا بشكل غير مباشر.
متباينة جنسن
متباينة جنسن (Jensen’s Inequality) هي ملاحظة هندسية تنص على: إذا كانت لدينا دالة محدبة، فإن توقع لهذه الدالة، على مدى النطاق، يكون أقل من متوسط الدالة التي تم تقييمها في بداية النطاق ونهايته. أنه أمر بديهي للغاية من الناحية الهندسية:
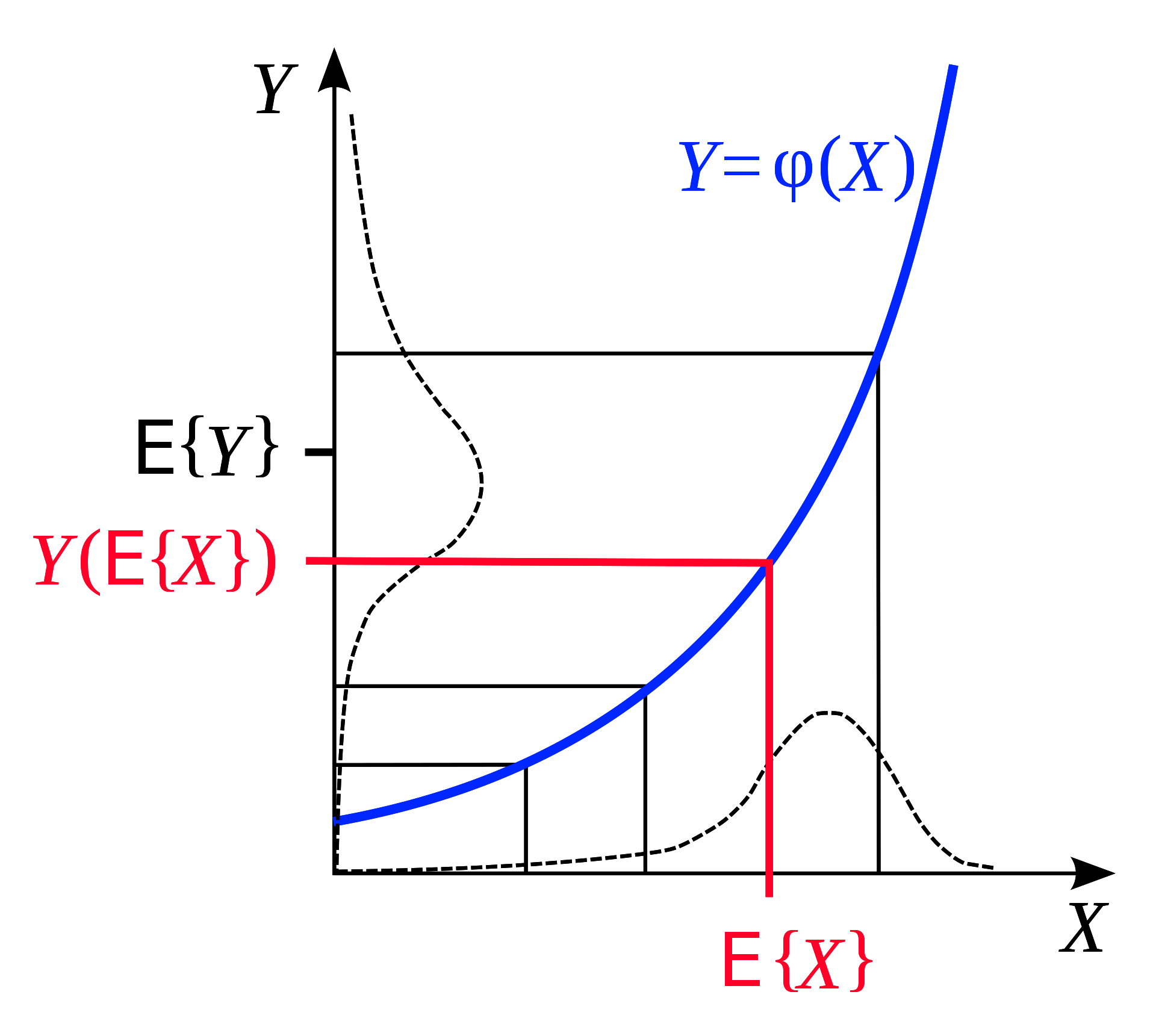
الشكل 6: متباينة ينسن (مأخوذة من [ويكيبيديا](https://en.wikipedia.org/wiki/Jensen%27s_inequality))
وبالمثل، إذا كان $F$ محدبًا، لتوزيع احتمالية ثابتة $q$، يمكننا أن نستنتج من تباين جنسن أنه في النطاق $z$،
\[F\Bigg(\int_z q(z)h(z)\Bigg) \leq \int_z q(z)F(h(z)) \tag{1}\]لآن، تذكر أن $L(x,y)$ المهمش بعد الضرب في $\frac{q(z)}{q(z)}$ هو،
\[L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\]إذا صنعنا $h(z) = -\frac{1}{\beta} \frac{\exp({-\beta E(x,y,z)})}{q(z)}$، نعلم من تباين جنسن $(1)$ ذلك
\[F\Bigg(\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z)F\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\]دعنا نواصل عمل هذا، مع دالة خسارة محدبة محددة, $F(x) = -\log(x)$
\[-\log\Bigg(-\frac{1}{\beta}\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z) * \frac{-1}{\beta}\log\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\] \[\leq \int_z q(z)[E(x,y,z) + \frac{1}{\beta}\log(q(z))]\] \[\leq \int_z q(z)E(x,y,z) + \frac{1}{\beta}\int_z q(z)\log(q(z))\]عظيم! الآن لدينا حد أعلى لدالة الخسارة $L(x,y)$، وهي تتألف من حدين نفهمهما. المصطلح الأول $\int_z q(z)E(x,y,z)$ هو * متوسط * الطاقة. والمصطلح الثاني $\frac{1}{\beta}\int_z\log(q(z))$ هو مجرد بعض العوامل ($-\frac{1}{\beta}$) مضروبًا في إنتروبيا التوزيع $q$.
ما هو بيت القصيد؟
لقد قمنا الآن بصياغة حد أعلى بطريقة يمكننا من خلالها تجنب عمليات الدمج المعقدة، وبدلاً من ذلك نقوم ببساطة بتقريب هذه القيم عن طريق أخذ عينات من توزيع بديل ($q(z)$)، من اختيارنا!
للحصول على قيمة المصطلح الأول لدالة الحد الأعلى، نقوم فقط بأخذ عينات من هذا التوزيع، وحساب متوسط قيمة $L$ الذي نحصل عليه من تطبيق $z$ الذي تم أخذ عينات منه.
المصطلح الثاني (عامل إنتروبيا) هو مجرد خاصية لمجموعة التوزيع، ويمكن أيضًا تقريبه بأخذ عينات عشوائية بقيمة $q$.
أخيرًا، يمكننا تصغير $L$ فيما يتعلق بمعاملاته (على سبيل المثال، أوزان الشبكة $W$)، عن طريق تقليل هذه الدالة التي تحدد أعلاه. نجري هذا التصغير عن طريق تحديث المتغيرين لدينا: (1) إنتروبيا $q$، و (2) معاملات النموذج $W$.
ملخص
هذه هي “وجهة نظر الطاقة” للتنبؤ المتغير. إذا كنت بحاجة إلى حساب لوقاريثم المجموع الأسي log of a sum of exponentials، فاستبدله بمتوسط دالتك بالإضافة إلى ثابت إنتروبيا والذي يعطينا الحد الأعلى. ثم نقوم بتقليل هذا الحد الأعلى، وبذلك نقلل من الدالة التي نريدها.
📝 Yada Pruksachatkun, Ananya Harsh Jha, Joseph Morag, Dan Jefferys-White, and Brian Kelly
Anass El Houd
4 May 2020