شبكات المخططات الإلتفافية III

مدخل إلى شبكة المخططات الإلتفافية (GCN)

خلاصة: الاهتمام الذاتي

• في الاهتمام الذاتي ، لدينا مجموعة من المدخلات $lbrace\boldsymbol{x}_{i}\rbrace^{t}_{i=1}$. على عكس التسلسل ، ليس له ترتيب.
• المتجه المخفي $boldsymbol{h}$ يُعطى بالتوليفة الخطية للمتجهات في المجموعة.
• يمكننا التعبير عن هذا كـ $boldsymbol{X}\boldsymbol{a}$ باستخدام ضرب متجه المصفوفة، حيث يحتوي $boldsymbol{a}$ على معاملات تقيس متجه الإدخال $boldsymbol{x}_{i}$.

تأشير

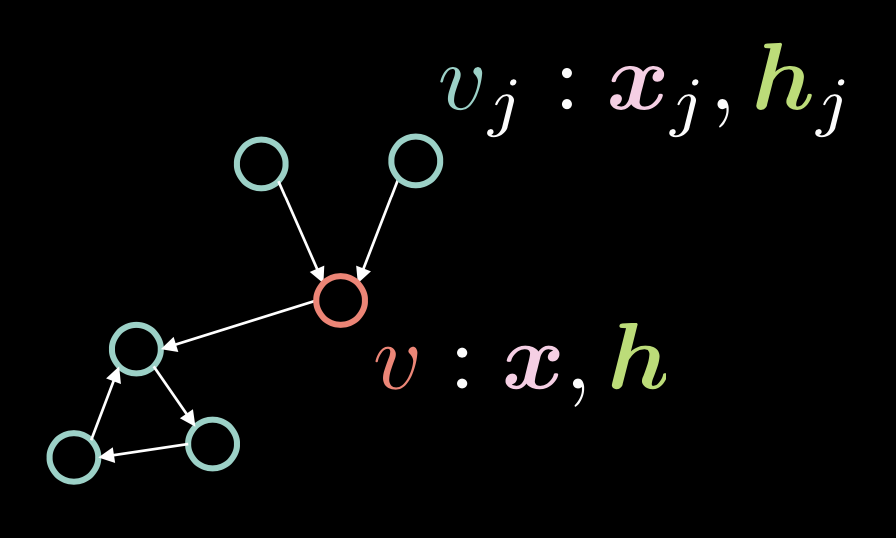
Fig. 1: Graph Convolutional Network

في الشكل 1 ، يتكون الرأس ‪$‬v‪$‬ من متجهين:الإدخال $boldsymbol{x}$ وتمثيله المخفي $boldsymbol{h}$. لدينا أيضًا رؤوس متعددة $v_ {j}$، والتي تتكون من $boldsymbol{x}_j$ و $boldsymbol{h}_j$. في هذا المخطط ، ترتبط الرؤوس بحواف موجهة.

نمثل هذه الحواف الموجهة مع المتجه المجاور $boldsymbol{a}$، حيث يأخذ كل عنصر $alpha_{j}$ القيمة $1$ إذا كان هناك حافة موجهة من $v_{j}$ إلى $v$.

تُعرَّف الدرجة $d$ (عدد الحواف الواردة) على أنها معيار متجه التقارب هذا، * مثال * $\Vert\boldsymbol{a}\Vert_{1}$ ، الذي يمثل عدد الآحاد في المتجه $boldsymbol{a}$.

المتجه المخفي $boldsymbol{h}$ يعطى بالتعبير التالي:

حيث أن $f(\cdot)$ هي دالة غير خطية مثل السيجمويد $\sigma(\cdot)$، والظل الهُذْلولي $\tanh(\cdot)$.

تأخذ العبارة $boldsymbol{U}\boldsymbol{x}$ في الحسبان الرأس $v$ نفسه، من خلال تطبيق الدوران $boldsymbol{U}$ على الإدخال $v$.

تذكر أنه في حالة الانتباه الذاتي ، يتم حساب المتجه المخفي $boldsymbol{h}$ بواسطة $boldsymbol{X}\boldsymbol{a}$، مما يعني أن الأعمدة الموجودة في $boldsymbol{X}$ تم تحجيمها بواسطة العوامل في $boldsymbol{a}$. في سياق GCN ، هذا يعني أنه إذا كان لدينا حواف واردة متعددة ، * أي * حواف متعددة في المتجه المجاور $\boldsymbol{a}$ فإن $\boldsymbol{X}\boldsymbol{a}$ يصبح أكبر. من ناحية أخرى ، إذا كان لدينا ميزة واردة واحدة فقط ، فإن هذه القيمة تصبح أصغر. لمعالجة هذه المشكلة المتعلقة بتناسب القيمة مع عدد الحواف الواردة ، نقوم بقسمتها على عدد الحواف الواردة $ d $. ثم نطبق الدوران $boldsymbol{V}$ على$\boldsymbol{X}\boldsymbol{a}d^{-1}$ .

يمكننا تمثيل هذا التمثيل المخفي $boldsymbol{h}$ لمجموعة المدخلات بالكامل $boldsymbol{x}$ باستخدام تدوين المصفوفة التالي:

حيث $vect{D} = \text{diag}(d_{i})$.

البوابات المتبقية GCN النظرية والكود

الشبكة الإلتفافية لمخطط البوابات المتبقية هي نوع ينتمي لعائلة GCN و يمكن تمثيلها كما هو موضح في الشكل 2:

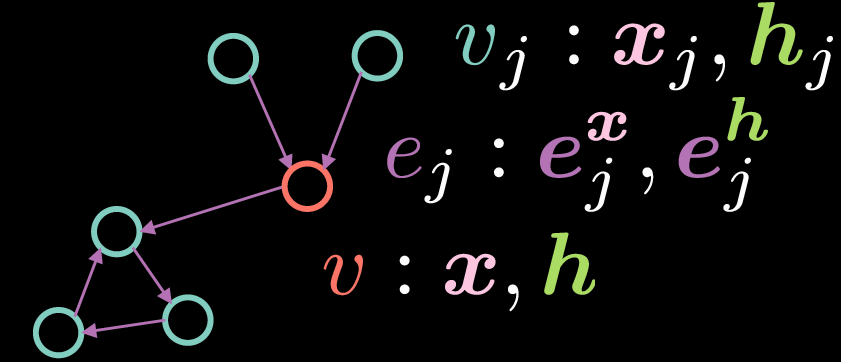
Fig. 2: Residual Gated Graph Convolutional Network

كما هو الحال مع GCN القياسي ، يتكون الرأس $v$ من متجهين: الإدخال $\boldsymbol{x}$ وتمثيله المخفي $boldsymbol{h}$. ومع ذلك، في هذه الحالة، تحتوي الحواف أيضًا على تمثيل للميزة، حيث يمثل $boldsymbol{e_{j}^{x}}$ تمثيل حافة الإدخال ويمثل $boldsymbol{e_{j}^{h}}$ تمثيل الحافة المخفية.

يتم حساب التمثيل المخفي $boldsymbol{h}$ للقمة $v$ بالمعادلة التالية:

حيث يمثل $boldsymbol{x}$ تمثيل الإدخال ، يمثل $boldsymbol{Ax}$ دورانًا مطبقًا على الإدخال $boldsymbol{x}$ و يشير $sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}}$ إلى مجموع الجداء العنصري للميزات الواردة التي تم تدويرها. على النقيض من GCN القياسي أعلاه حيث نقوم بتوسيط التمثيلات الواردة ، فإن مصطلح البوابة ضروري لتنفيذ البقايا المبوبة GCN لأنه يسمح لنا بتعديل التمثيلات الواردة بناءً على تمثيلات الحافة.

لاحظ أن التجميع يقع فقط فوق الرؤوس ${v_j}$ التي لها حواف واردة للرأس ${v}$. المصطلح المتبقي (في Residual Gated GCN) يأتي من حقيقة أنه من أجل حساب التمثيل المخفي $boldsymbol{h}$ ، نضيف تمثيل الإدخال $ boldsymbol{x}$. يتم حساب مصطلح البوابة $eta(\boldsymbol{e_{j}})$ كما هو موضح أدناه:

قيمة البوابة $eta(\boldsymbol{e_{j}})$ هي عبارة عن سيجمويد مسواة تم الحصول عليها بقسمة السيجمويد الخاص بتمثيل الحافة الواردة على مجموع السيجمويد لجميع تمثيلات الحواف الواردة. لاحظ أنه من أجل حساب مصطلح البوابة ، نحتاج إلى تمثيل الحافة $boldsymbol{e_{j}}$، والتي يمكن حسابها باستخدام المعادلات أدناه:

يتم الحصول على تمثيل الحافة المخفية $boldsymbol{e_{j}^{h}}$ من خلال جمع تمثيل الحافة الأولية $boldsymbol{e_{j}^{x}}$ أما $texttt{ReLU}(\cdot)$ فيتم تطبيقه على $boldsymbol{e_{j}}$ حيث يتم إعطاء $boldsymbol{e_{j}}$ بدوره من خلال جمع الاستدارة المطبقة على $boldsymbol{e_{j}^{x}}$ ، استدارة مطبقة على تمثيل الإدخال $boldsymbol{x_{j}}$ للرأس $ v_ {j} $ وتم استدارة مطبقة على تمثيل الإدخال $boldsymbol{x}$ للرأس $v$.

• ملاحظة: من أجل حساب التمثيلات المخفية في اتجاه مجرى النهر (* على سبيل المثال * طبقة التمثيلات المخفية الثانية) ، يمكننا ببساطة استبدال تمثيلات ميزة الإدخال عن طريق تمثيلات ميزة الطبقة الأولى في المعادلات أعلاه. *

تصنيف المخطط وطبقة البوابات المتبقية GCN

في هذا القسم ، نقدم مشكلة تصنيف المخطط وتشفير طبقة البوابات المتبقية GCN. بالإضافة إلى عبارات الاستيراد المعتادة ، نضيف ما يلي:

os.environ['DGLBACKEND'] = 'pytorch'
import dgl
from dgl import DGLGraph
from dgl.data import MiniGCDataset
import networkx as nx

السطر الأول يخبر DGL باستخدام PyTorch كخلفية. توفر مكتبة المخطط العميق ([DGL] (https://www.dgl.ai/)) وظائف متنوعة على المخططات بينما تسمح لنا networkx برؤية المخططات.

في دفتر الملاحظات هذا ، تتمثل المهمة في تصنيف بنية مخطط معينة إلى نوع من أنواع المخططات الثمانية. تنتج مجموعة البيانات التي تم الحصول عليها من dgl.data.MiniGCDataset عددًا من المخططات (num_graphs) مع عقد بين min_num_v و max_num_v. وبالتالي ، فإن جميع المخططات التي تم الحصول عليها لا تحتوي على نفس عدد العقد / الرؤوس.

• ملاحظة: من أجل التعرف على أساسيات “DGLGraphs” ، يوصى بالاطلاع على البرنامج التعليمي القصير [هنا] (https://docs.dgl.ai/api/python/graph.html). *

بعد إنشاء المخططات ، فإن المهمة التالية هي إضافة بعض الإشارات إلى المجال. يمكن تطبيق الميزات على عقد وحواف “DGLGraph”. يتم تمثيل الميزات كقاموس للأسماء (سلاسل) وموترات (** الحقول **). ndata و edata` هي عبارة عن سكر لغوي للوصول إلى بيانات ميزات جميع العقد والحواف.

يوضح مقتطف الشفرة التالي كيفية إنشاء الميزات. يتم تعيين قيمة مساوية لعدد حواف العارضة لكل عقدة ، بينما يتم تعيين القيمة 1 لكل حافة.

def create_artificial_features(dataset):
    for (graph, _) in dataset:
        graph.ndata['feat'] = graph.in_degrees().view(-1, 1).float()
        graph.edata['feat'] = torch.ones(graph.number_of_edges(), 1)
    return dataset

يتم إنشاء مجموعات بيانات التدريب والاختبار وتعيين الميزات كما هو موضح أدناه:

trainset = MiniGCDataset(350, 10, 20)
testset = MiniGCDataset(100, 10, 20)

trainset = create_artificial_features(trainset)
testset = create_artificial_features(testset)

يحتوي نموذج المخطط من trainset على التمثيل التالي. هنا ، نلاحظ أن المخطط يحتوي على 15 عقدة و 45 حافة وأن كل من العقد والحواف لها تمثيل مميز للشكل “(1)” كما هو متوقع. علاوة على ذلك ، يشير “0” إلى أن هذا المخطط ينتمي إلى الفئة 0.

(DGLGraph(num_nodes=15, num_edges=45,
         ndata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}
         edata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}), 0)

ملاحظة حول رسالة DGL وتقليل الوظائف

في DGL ، يتم التعبير عن * وظائف الرسالة * كـ (وظائف من تحديد المستخدم) Edge UDF. تأخذ Edge UDFs وسيط واحد edges`. يحتوي على ثلاثة أعضاء “src” و “dst” و “data” للوصول إلى ميزات عقدةالمصدر، ميزات عقدة الوجهة، وميزات الحافة على التوالي.

• وظائف التقليل * هي عقد ‪‬UDF‪‬. تحتوي عقد UDFs على وسيط واحد “عُقد” ، والتي تحتوي على عضوين هما “data” و “mailbox”. تحتوي “data” على ميزات العقدة ويحتوي “mailbox” على جميع ميزات الرسائل الواردة ، مكدسة على طول البعد الثاني (ومن ثم الوسيطة “dim = 1”). ʻupdate_all (message_func، Red_func) `يرسل الرسائل عبر جميع الحواف

[التطبيق البرمجي لطبقة البوابات المتبقية GCN] (https://www.youtube.com/watch؟v=2aKXWqkbpWg&list=PLLHTzKZVU9eaEyErdV26ikyolxOsz6mq&index=25&t=2098s)

يتم تنفيذ طبقة GCN المتبقية ذات البوابات كما هو موضح في مقتطفات التعليمات البرمجية أدناه.

أولاً ، جميع التدويرات لميزات الإدخال $boldsymbol{Ax}$، $\boldsymbol{Bx_{j}}$، $\boldsymbol{Ce_{j}^{x}}$، $\boldsymbol{Dx_{j}}$ و $boldsymbol{Ex}$ يتم حسابهما من خلال تحديد طبقات nn.Linear داخل وظيفة__init__ ثم إعادة توجيه تمثيلات الإدخال h و ʻe عبر الطبقات الخطية داخل وظيفة forward`

class GatedGCN_layer(nn.Module):

    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.A = nn.Linear(input_dim, output_dim)
        self.B = nn.Linear(input_dim, output_dim)
        self.C = nn.Linear(input_dim, output_dim)
        self.D = nn.Linear(input_dim, output_dim)
        self.E = nn.Linear(input_dim, output_dim)
        self.bn_node_h = nn.BatchNorm1d(output_dim)
        self.bn_node_e = nn.BatchNorm1d(output_dim)

ثانيًا ، نحسب تمثيلات الحواف. يتم ذلك داخل وظيفة message_func ، التي تتكرر عبر جميع الحواف وتحسب تمثيلات الحواف. على وجه التحديد ، السطر e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh'] يحسب * (المعادلة 7) * من أعلى. تشحن Bh_j بالوظيفة message_func (وهو $boldsymbol{Bx_{j}}$ من (المعادلة 5)) و ʻe_ij` (المعادلة 7) عبر الحافة إلى صندوق بريد عقدة الوجهة.

def message_func(self, edges):
    Bh_j = edges.src['Bh']
    # e_ij = Ce_ij + Dhi + Ehj
    e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']
    edges.data['e'] = e_ij
    return {'Bh_j' : Bh_j, 'e_ij' : e_ij}

ثالثًا ، تقوم وظيفة “reduce_func” بتجميع الرسائل المشحونة بواسطة الوظيفة “message_func”. بعد جمع بيانات العقدة ‪’‬Ah‪’‬ وشحن البيانات Bh_j و ʻe_ij من صندوق البريد ، السطر h = Ah_i + torch.sum (sigma_ij * Bh_j، dim = 1) / torch.sum (sigma_ij، dim = 1) `يحسب التمثيل الخفي لكل عقدة كما هو مبين في (المعادلة 5). مع ذلك ، لاحظ أن هذا لا يمثل سوى المصطلح $(boldsymbol{Ax} + \sum_{v_j → v} {\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ بدون $ texttt{ReLU}(\cdot)$ و الوصلة المتبقية.

def reduce_func(self, nodes):
    Ah_i = nodes.data['Ah']
    Bh_j = nodes.mailbox['Bh_j']
    e = nodes.mailbox['e_ij']
    # sigma_ij = sigmoid(e_ij)
    sigma_ij = torch.sigmoid(e)
    # hi = Ahi + sum_j eta_ij * Bhj
    h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)
    return {'h' : h}

داخل وظيفة forward ، بعد استدعاء g.update_all ، نحصل على نتائج المخطط الإلتفافي h و ʻe ، والتي تمثل المصطلحين $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ من(المعادلة 5) و $boldsymbol{e_{j}}\$ من (المعادلة 7) على التوالي. بعد ذلك ، نقوم بتسوية "h" و "e" فيما يتعلق بحجم عقد وحواف المخطط على التوالي. ثم يتم تطبيق تسوية الحزم حتى نتمكن من تدريب الشبكة بشكل فعال. أخيرًا ، نطبق $texttt{ReLU}(\cdot)\$ ونضيف الوصلات المتبقية للحصول على التمثيلات المخفية للعقد والحواف ، والتي يتم إرجاعها بعد ذلك بواسطة وظيفة forward`.

def forward(self, g, h, e, snorm_n, snorm_e):

    h_in = h # residual connection
    e_in = e # residual connection

    g.ndata['h']  = h
    g.ndata['Ah'] = self.A(h)
    g.ndata['Bh'] = self.B(h)
    g.ndata['Dh'] = self.D(h)
    g.ndata['Eh'] = self.E(h)
    g.edata['e']  = e
    g.edata['Ce'] = self.C(e)

    g.update_all(self.message_func, self.reduce_func)

    h = g.ndata['h'] # result of graph convolution
    e = g.edata['e'] # result of graph convolution

    h = h * snorm_n # normalize activation w.r.t. graph node size
    e = e * snorm_e # normalize activation w.r.t. graph edge size

    h = self.bn_node_h(h) # batch normalization
    e = self.bn_node_e(e) # batch normalization

    h = torch.relu(h) # non-linear activation
    e = torch.relu(e) # non-linear activation

    h = h_in + h # residual connection
    e = e_in + e # residual connection

    return h, e

بعد ذلك، نحدد وحدة MLP_Layer التي تحتوي على عدة طبقات متصلة بالكامل (FCN). نقوم بإنشاء قائمة من الطبقات المتصلة بالكامل ونقوم بإعادة توجيهها عبر الشبكة.

أخيرًا ، نقوم بتعريف نموذج “GatedGCN” الخاص بنا والذي يتكون من الفئات المحددة مسبقًا: “GatedGCN_layer” و “MLP_layer”. تعريف نموذجنا (“GatedGCN”) موضح أدناه.

 class GatedGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, L):
        super().__init__()
        self.embedding_h = nn.Linear(input_dim, hidden_dim)
        self.embedding_e = nn.Linear(1, hidden_dim)
        self.GatedGCN_layers = nn.ModuleList([
            GatedGCN_layer(hidden_dim, hidden_dim) for _ in range(L)
        ])
        self.MLP_layer = MLP_layer(hidden_dim, output_dim)
    def forward(self, g, h, e, snorm_n, snorm_e):
        # input embedding
        h = self.embedding_h(h)
        e = self.embedding_e(e)
        # graph convnet layers
        for GGCN_layer in self.GatedGCN_layers:
            h, e = GGCN_layer(g, h, e, snorm_n, snorm_e)
        # MLP classifier
        g.ndata['h'] = h
        y = dgl.mean_nodes(g,'h')
        y = self.MLP_layer(y)
        return y

في المُنشئ الخاص بنا ، نحدد التضمينات لـ ‪’‬e‪’‬ و h ( self.embedding_e و self.embedding_h) ، و self.GatedGCN_layer وهي قائمة (حجمها $L$) لنموذجنا المحدد مسبقًا : “GatedGCN_layer” ، وأخيرًا “self.MLP_layer” والذي تم تعريفه أيضًا من قبل. بعد ذلك ، باستخدام هذه التهيئة ، نحن ببساطة نعيد توجيهها عبر النموذج والمخرج y.

لفهم النموذج بشكل أفضل ، نهيئ كائنًا من النموذج ونطبعه للحصول على تصور أفضل:

# instantiate network
model = GatedGCN(input_dim=1, hidden_dim=100, output_dim=8, L=2)
print(model)

الهيكل الرئيسي للنموذج مبين أدناه:

GatedGCN(
  (embedding_h): Linear(in_features=1, out_features=100, bias=True)
  (embedding_e): Linear(in_features=1, out_features=100, bias=True)
  (GatedGCN_layers): ModuleList(
    (0): GatedGCN_layer(...)
    (1): GatedGCN_layer(... ))
  (MLP_layer): MLP_layer(
    (FC_layers): ModuleList(...))

ليس من المستغرب أن لدينا طبقتان من “GatedGCN_layer” (منذ “L = 2”) متبوعًا بـ “MLP_layer” والذي ينتج أخيرًا مخرجا من 8 قيم.

من الآن فصاعدًا ، نحدد وظيفتي train و evaluate. في وظيفة train ، لدينا الكود العام الذي يأخذ عينات من dataloader. بعد ذلك ، يتم إدخال batch_graphs ،batch_x ،batch_e, batch_snorm_n و batch_snorm_e لتغذية نموذجنا الذي يُرجع batch_scores (بحجم 8). تتم مقارنة الدرجات المتوقعة بالحقيقة الأساسية في وظيفة الخسارة لدينا:loss(batch_scores, batch_labels). بعد ذلك ، نحذف التدرجات (optimizer.zero_grad()) وننفذ الانتشار الخلفي(J.backward()) ونحدّث أوزاننا (optimizer.step()). أخيرًا ، يتم حساب الخسارة الحقبة ودقة التدريب. علاوة على ذلك ، نستخدم رمزًا مشابهًا لوظيفة evaluate الخاصة بنا.

أخيرًا ، نحن مستعدون للتدريب! وجدنا أنه بعد 40 حقبة من التدريب ، تعلم نموذجنا تصنيف الرسوم البيانية بدقة اختبار تبلغ 87 في المائة.