شبكات المخططات الطيفية الإلتفافية I

🎙️ Xavier Bresson

[ConvNets التقليدية] (https://www.youtube.com/watch?v=Iiv9R6BjxHM&list=PLLHTzKZzVU9eaEyErdV26ikyolxOsz6mq&index=24&t=50s)

تعتبر ConvNets هياكل قوية لحل مشاكل التعلم عالية الأبعاد

ما هو بلاء الأبعاد ؟

لنأخذ على سبيل المثال صورة ذات حجم 1024 × 1024 بكسل. يمكن رؤية هذه الصورة كنقطة في الفضاء ذو 1،000،000 بعد. يؤدي استخدام 10 عينات لكل بُعد إلى إنتاج $ {10} ^ {1،000،000} $ صورة ، وهو مبلغ مرتفع للغاية. تعد شبكة ConvNets قوية للغاية لاستخراج أفضل تمثيل لبيانات الصور عالية الأبعاد ، مثل تلك الواردة في المثال.

• أبعاد (الصورة) = 1024x1024 = ${10}^{6}$

• إذا كان ‪‬ ‪=‬ 10 N‪‬ عينة لكل بُعد ، الذي يعطينا ‪‬ ${10}^{1,000,000}$ ‪‬ نقطة

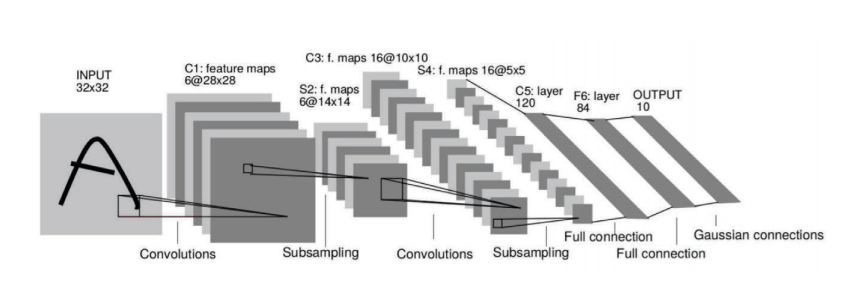
.1 الشكل : تمثيل بيانات الصورة عالية الأبعاد تستخلص ConvNets.

الافتراضات الرئيسية حول ConvNets

** 1. البيانات (الصور، مقاطع الفيديو، والكلام) هي تركيبية. **

تتكون من أنماط التي تكون:

• ** محلية ** العصبون في الشبكة العصبية يكون متصلا بالطبقات المجاورة فقط، ولكن ليس بجميع الطبقات في الشبكة. نسمي هذا افتراض مجال الاستقبال المحلي.
• ** ثابتة ** لدينا بعض الأنماط المتشابهة ويتم مشاركتها عبر مجال الصور الخاص بنا. على سبيل المثال ، ملاءة السرير الصفراء في الصورة الوسطى من الشكل 2.
• ** هرمية ** سيتم دمج ميزات المستوى المنخفض لتشكيل ميزات متوسطة المستوى. بعد ذلك ، سيتم دمج ميزات المستوى المتوسط هذه بشكل تدريجي لتشكيل ميزات ذات مستوى أعلى وأعلى. على سبيل المثال ، تمثيل مرئي.

. الشكل 2: البيانات تركيبية.

** 2. ConvNets تستفيد من بنية التكوين . **

إنهم يستخرجون الميزات التركيبية ويغذون بها المصنف ، المُوَصّي ، إلخ.

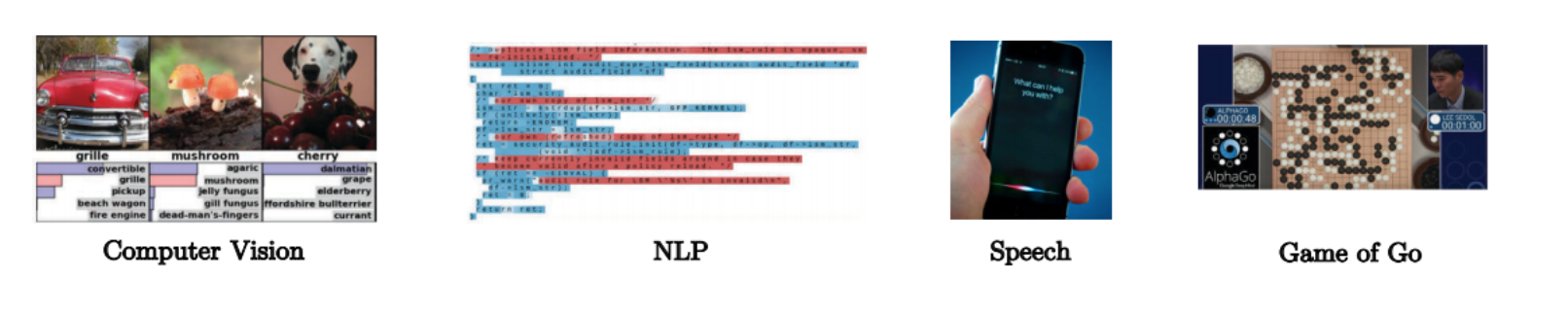
.3 الشكل : تستفيد ConvNets من بنية التكوين.

مجال المخططات

مجال البيانات

• الصور،الأحجام، ومقاطع الفيديو تقع على مجالات 2D ، 3D ، 2D + 1 الإقليدية (الشبكات)‪.‬ كل بكسل يتم تمثيله بواسطة متجه مكون من قيم اللون الأحمر، الأخضر، والأزرق.

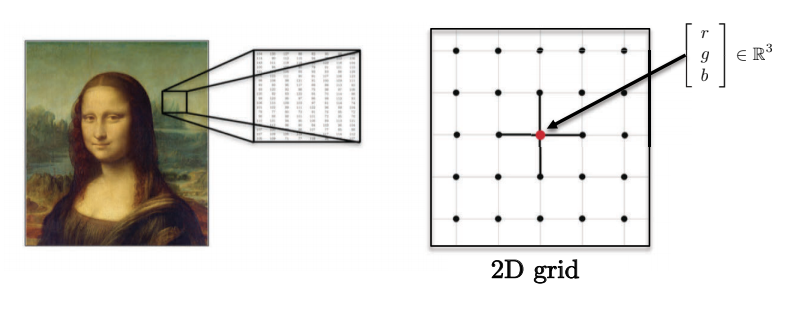
.4 الشكل : الصور لها أبعاد متعددة.

• الجمل ، الكلمات ، الكلام الكامن في المجال الإقليدي أحادي البعد. على سبيل المثال يمكن تمثيل كل حرف بعدد صحيح.

  
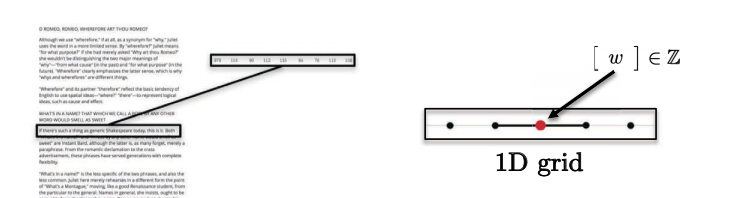
  .5 الشكل : التسلسلات لها بعد واحد.

• تحتوي هذه المجالات على هياكل مكانية منتظمة قوية، مما يسمح لجميع عمليات ال ConvNets أن تكون سريعة ومحددة جيدًا من الناحية الحسابية.

  
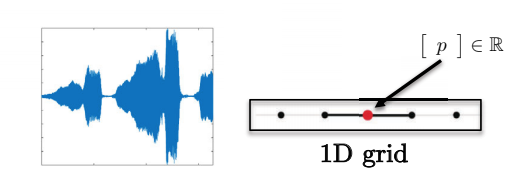
  .6 الشكل : بيانات الكلام لها شبكة أحادية البعد.

مجال المخططات

أمثلة تحفيزية لمجالات المخططات

لنأخذ على سبيل المثال شبكة اجتماعية. يتم التقاط الشبكة الاجتماعية بشكل أفضل من خلال تمثيل المخططات لأن الاتصال الثنائي بين مستخدمين لا يشكل شبكة. تمثل العُقد مخططات المستخدمين ، بينما تمثل الحواف بين عقدتين الوصلة بين عقدتين (مستخدمين). لكل مستخدم مصفوفة ميزات ثلاثية الأبعاد تحتوي على رسائل، صور، ومقاطع فيديو.

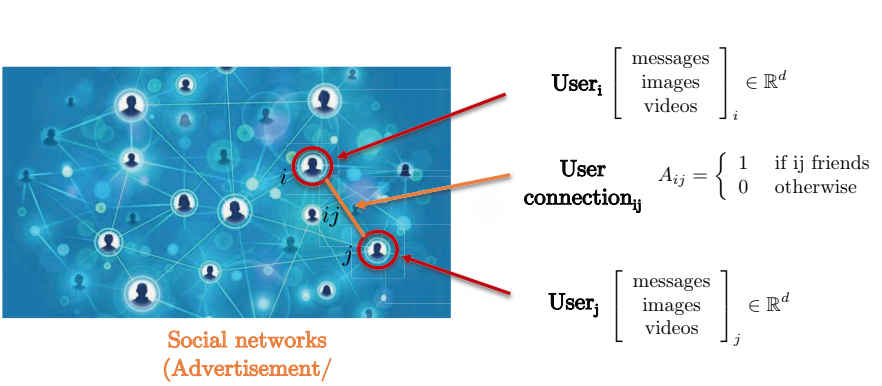
.7 الشكل :الشبكات الاجتماعية عن طريق المخططات.

تقدم الوصلة بين بنية ووظيفة الدماغ للتنبؤ بالأمراض الوراثية العصبية مثالًا تحفيزيًا يجب مراعاته. كما يتضح أدناه ، يتكون الدماغ من عدة مناطق اهتمام (ROI). ترتبط مناطق الإهتمام محليًا ببعض مناطق الاهتمامات المحيطة بها فقط. تمثل مصفوفة المُتَاخَمَة ‪(المُجَاوَرَة)‬ درجة القوة بين مناطق الاهتمام المختلفة.

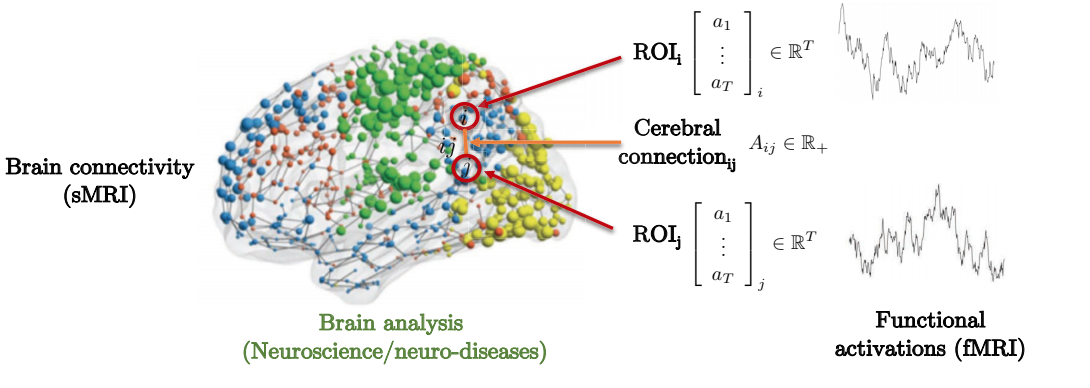
.8 الشكل : اتصال الدماغ عن طريق تمثيل المخططات.

تقدم كيمياء الكم أيضًا تمثيلًا مثيرًا للاهتمام لمجال المخططات. يتم تمثيل كل ذرة بواسطة عقدة في المخطط والتي بدورها ترتبط بالذرات الأخرى من خلال روابط باستخدام الحواف. كل من هذه الجزيئات / الذرات لها مميزات مختلفة ، مثل الشحنة ونوع الرابطة المتعلق بها وما إلى ذلك.

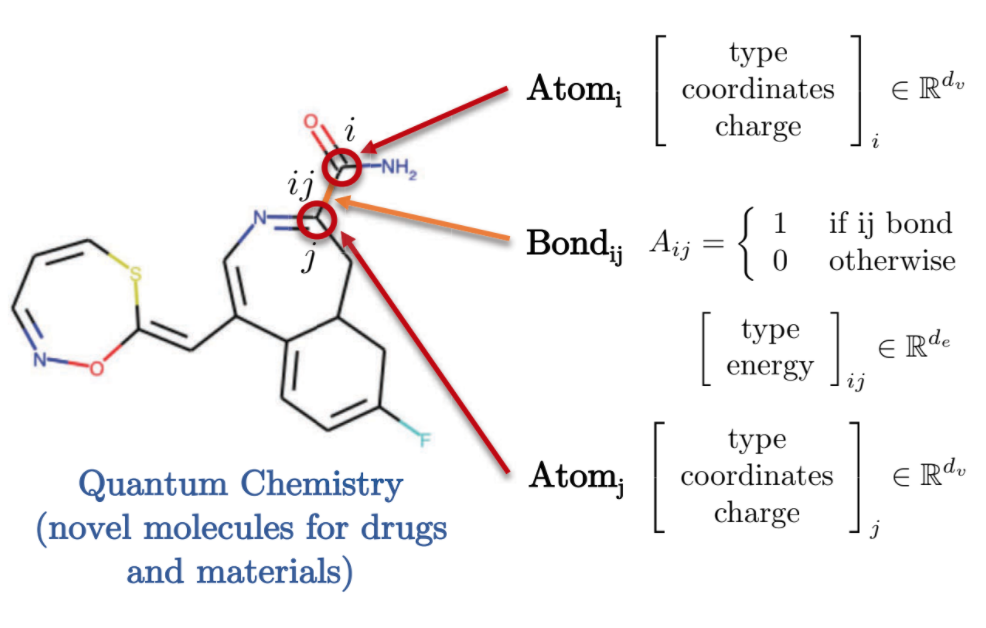
.9 الشكل : كيمياء الكم عن طريق تمثيل المخططات.

تعريف المخطط وخصائصه

• يتم تعريف المخطط G من خلال:
  • ** الرؤوس V **
  • ** الحواف E **
  • ** مصفوفة المُجَاوَرَة A **
• ميزات المخطط:
  • ** ميزات العقدة: $ h_ {i} $، $ h_ {j} $ ** (نوع الذرة)
  • ** ميزات الحافة: $ e_ {ij} $ ** (نوع السند)
  • ** ميزات المخطط: ** g (طاقة الجزيء)

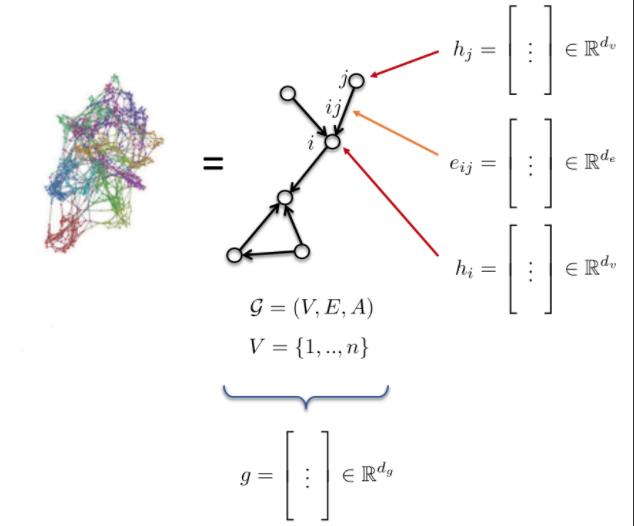
.10 الشكل : المخطط.

## الشبكات الإلتفافية التقليدية (https://www.youtube.com/watch?v=Iiv9R6BjxHM&list=PLLHTzKZzVU9eaEyErdV26ikyolxOsz6mq&index=24&t=791s)

الإلتفاف

يمكن تعريف الإلتفاف بشكل موجز كما يلي:

\(h ^ {\ell + l} = w ^ \ell * h ^ \ell،\) حيث $h^{\ell+1}$ is $n_1\times n_2\times d$-dimensional, $w^\ell$ is $3\times 3\times d$-dimensional, and $h^\ell$ is $n_1\times n_2\times d$-dimensional. على سبيل المثال ، $ n_1 $ و $ n_2 $ يمكن أن تمثل عدد البكسل في الاتجاهين $x$ و $y$ للصورة ، على التوالي ، و $ d $ هو أبعاد كل بكسل (* على سبيل المثال * ، 3 للصور الملونة).
وعليه ، $ h ^ {\ ell + 1} $ تمثل ميزة في الطبقة المخفية $ ( ell + 1) $ تم الحصول عليها من خلال تطبيق الإلتفاف $w^\ell$ على ميزة في الطبقة ال $ ell\ $ .
عادةً ما تكون النواة صغيرة لتمثيل حقل استقبال محلي‪$‬3 \times 3‪$‬ في هذه الحالة ، أو ‪$‬5 \times 5‪$‬ ، على سبيل المثال.
ملاحظة: نستخدم الحشو للتأكد من أن أبعاد $ h ^ {\ell + 1} $ هي نفسها أبعاد $ h ^ \ell $. \

على سبيل المثال ، في هذه الصورة ، يمكن استخدام النواة للتعرف على الخطوط.

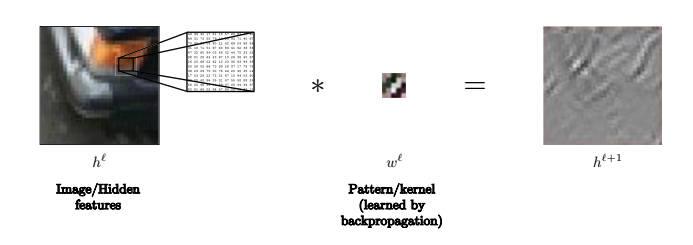
.11 الشكل : يمكن استخدام النواة للتعرف على الخطوط في الصور.

كيف نعرف الإلتفاف؟

بشكل أكثر دقة ، يتم تعريف الإلتفاف على النحو التالي:

\[h_i^{\ell+1} = w^\ell * h_i^\ell\] \[= \sum_{j\in\Omega}\langle w_j^\ell, h_{i-j}^\ell\rangle\] \[= \sum_{j\in\mathcal{N}_i} \langle w_j^\ell, h_{ij}^\ell\rangle\] \[=\sum_{j\in\mathcal{N}_i} \langle \Bigg[w_j^\ell\Bigg], \Bigg[h_{ij}\Bigg]\rangle\]

يعرّف ما ورد أعلاه الالتفاف على أنه * مطابقة القالب *. عادةً ما نستخدم $ h_ {i + j} $ بدلاً من $ h_ {i-j} $ ، لأن الأول هو في الواقع ارتباط ، وهو أشبه بمطابقة القالب.

ومع ذلك ، لا يهم حقًا إذا كنت تستخدم الأول أو الثاني ، لأن النواة الخاصة بك قد انقلبت فقط، وهذا لا يؤثر على التعلم.

في السطر الثالث ، نكتب $ h_{i + j} ^ \ell $ كـ $ h_{ij} ^ \ell $.

النواة صغيرة جدًا ، لذا فبدلاً من جمع الصورة بأكملها $ Omega\ $ ، كما في السطر الثاني ، نجمع في الواقع محيط الخلية ‪$‬i‪$‬ فقط ‪$‬\mathcal‪{‬N‪}_‬i‪$‬، كما هو موضح في السطر الثالث.

هذا يجعل من تعقيد الالتفاف هو $ O(n) $ ، حيث $ n $يمثل عدد البكسل في صورة الإدخال.

الالتفاف هو بالضبط لكل من $ n $ بكسل ، مجمعة على الجداءات الداخلية للمتجهات ذات البعد $ d $ مطبقة على شبكات ‪$‬3 \times 3‪$‬.

وبالتالي يكون التعقيد هو $ n \cdot 3 \cdot 3 \cdot d $ ، وهو $ O(n) $؛ علاوة على ذلك ، يمكن إجراء العمليات الحسابية على كل بكسل من وحدات البكسل $ n $ على حدة بالتوازي مع وحدات معالجة GPUs .

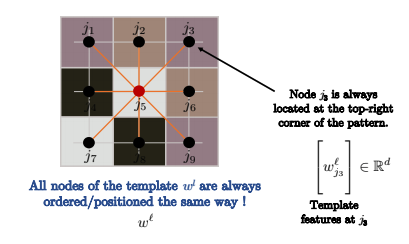
.12 الشكل : يتم ترتيب العقد بنفس الطريقة.

إذا كان المخطط الذي تقوم بالالتفاف عليه عبارة عن شبكة، كما هو الحال في الالتفاف القياسي على الصور في الرؤية الحاسوبية ، فإنه سيتم ترتيب العقد كما في الصورة أعلاه. لذلك ،$ j_3 $ سيكون دائمًا في الزاوية اليمنى العليا من النموذج.

وعليه، بالنسبة لجميع العقد $ i $ في الصورة أدناه مثل $ i $ و $‪’‬i$ ، فإن ترتيب العقدة في النواة هو نفسه دائمًا. على سبيل المثال، دائمًا نقارن $ j_3 $ في الزاوية اليمنى العليا للنمط مع الزاوية اليمنى العليا من مجزأ الصورة (ما نلتف حوله للبكسل $ i $) ، كما هو موضح أدناه. بتعبير رياضي:

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{ij_3}^\ell \Bigg]\rangle\]

و

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{i'j_3}^\ell \Bigg]\rangle\]

دائمًا للزاوية اليمنى العلوية بين القالب و مجزأ الصورة.

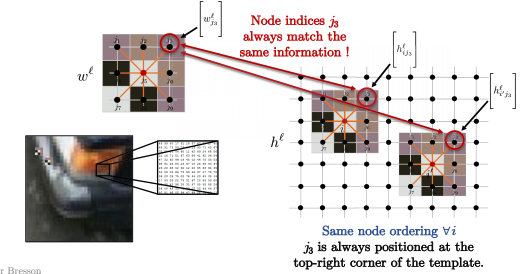
.13 الشكل : تتطابق أجزاء الصور مع القوالب.

هل يمكننا توسيع نطاق مطابقة القوالب للمخططات؟

لدينا بعض المشاكل:

1. أولاً ، في المخطط ، لا يوجد ترتيب للعقد.

لذلك في القالب الموضح أدناه في الصورة ، العقدة $ j_3 $ ليس لها موضع محدد ، ولكنها مجرد فهرس (عشوائي). لذلك ، عندما نحاول المطابقة مع العقدتين $ i $ و $ i ‘$ في المخطط أدناه ، لا نعرف ما إذا كان $ j_3 $ يطابق نفس العقد في كلا الالتفافين.
هذا بسبب عدم وجود فكرة * الزاوية اليمنى العليا * للمخطط.
لا توجد فكرة لأعلى ولأسفل ولليسار لليمين
وبالتالي ، فإن مطابقة القالب ليس لها في الواقع أي معنى ولا يمكننا استخدام تعريف مطابقة القالب مباشرة ، على النحو الوارد أعلاه.

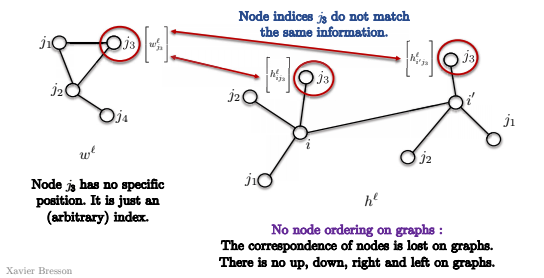
.14 الشكل : لا يوجد ترتيب عقدة في المخطط.

1. المشكلة الثانية هي أن أحجام التجاور قد تكون مختلفة.

لذا فإن القالب $ w ^ \ell $ الموضح أدناه يحتوي على 4 عقد ، لكن العقدة $ i $ بها 7 عقد في جوارها. فكيف يمكننا المقارنة بينهما؟

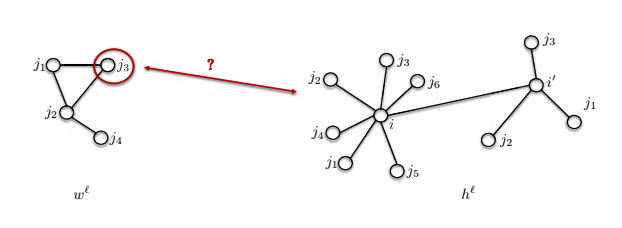
.15 الشكل : أحجام المجاورين تكون مختلفة في المخطط.

الإلتفاف المخطط

نستخدم الآن ** نظرية الإلتفاف ** لتعريف الإلتفاف للمخطط.

تنص ** نظرية الإلتفاف ** على أن تحويل فوريي لإلتفاف دالتين هو الجداء النقطي لتحويلي فوريي الخاص بهما:

\[\mathcal{F}(w*h) = \mathcal{F}(w) \odot \mathcal{F}(h) \implies w * h = \mathcal{F}^{-1}(\mathcal{F}(w)\odot\mathcal{F}(h))\]

بشكل عام ، يحتوي تحويل فوريي على $ O (n ^ 2) $ معقد ، ولكن إذا كان المجال شبكة ، فيمكن تقليل التعقيد إلى $ O (n \ log n) $ باستخدام FFT.

هل يمكننا توسيع نظرية الإلتفاف إلى المخططات؟

وهذا ينتج عنه سؤالين:

1. كيف نعرف تحويلات فوريي للمخططات؟
2. كيف يتم حساب إلتفافات طيفية سريعة في زمن قدره‪$‬O‪(‬n‪)$‬ للنَّوَى المدمجة (كما في مطابقة القالب)؟

\[w *_{\mathcal{G}} h \stackrel{?}{=} \mathcal{F}^{-1}_{\mathcal{G}}(\mathcal{F}_{\mathcal{G}}(w)\odot\mathcal{F}_{\mathcal{G}}(h))\]

سنستخدم هذين التصميمين للشبكات العصبية للمخططات: مطابقة القوالب ستكون لمخططات ConvNets المكانية وسيتم استخدام نظرية الالتفاف لشبكات ConvNets الطيفية.

(https://www.youtube.com/watch?v=Iiv9R6BjxHM&list=PLLHTzKZzVU9eaEyErdV26ikyolxOsz6mq&index=24&t=1529s) [ الطيفية ConvNets مخططات]

كيف يتم إجراء الالتواء الطيفي؟

الخطوة 1: مخطط لابلاسيان

هذا هو العامل الأساسي في نظرية المخطط الطيفي.

نعرف

\[\begin{aligned} \mathcal{G}=(V, E, A) & \rightarrow \underset{n \times n}{\Delta}=\mathrm{I}-D^{-1 / 2} A D^{-1 / 2} \\ & \quad \text { where } \underset{n \times n} D=\operatorname{diag}\left(\sum_{j \neq i} A_{i j}\right) \end{aligned}\]

لاحظ أن المصفوفة $ A $ هي مصفوفة المجاورة، و $Delta$ هي لابلاسيان، والتي تساوي المتطابقة مطروحًا منها المصفوفة المجاورة التي تم تسويتها بواسطة المصفوفة $ D $ والتي تمثل مصفوفة قطرية، وكل عنصر على القطر يمثل درجة العقدة. وهذا ما يسمى لابلاسيان المسوى ، أو لابلاسيان افتراضيًا في هذا السياق.

يتم تفسير لابلاسيان على أنه قياس نعومة المخطط ، وبعبارة أخرى ، الفرق بين القيمة المحلية $ h_i $ ومتوسط القيمة المجاورة لها البالغ $ h_j $. $ d_i $ في الصيغة أدناه هي درجة العقدة $ i $ ، و $mathcal{N}_{i}$ هي جميع العقد المجاورة للعقدة $ i $.

\[(\Delta h)_{i}=h_{i}-\frac{1}{d_{i}} \sum_{j \in \mathcal{N}_{i}} A_{i j} h_{j}\]

الصيغة أعلاه هي تطبيق لابلاسيان على الدالة $ h $ في العقدة $ i $ ، وهي قيمة $ h_i $ مطروحًا منها متوسط القيمة على العقد المجاورة لها ‪$‬h‪_‬j‪$‬. بشكل أساسي ، إذا كانت الإشارة سلسة جدًا ، تكون قيمة لابلاسيان صغيرة ، * والعكس صحيح *.

الخطوة الثانية: دوال فوريي

ما يلي هو التحليل الذاتي لمخطط لابلاسيان ،

\[\underset{n \times n}{\Delta}=\Phi^{T} \Lambda \Phi\]

يتم تقسيم لابلاسيان إلى ثلاث مصفوفات ، $Phi ^ T$ ، $ \Lambda $ ، $ \Phi\ $.

المصفوفة $Phi$ كما هي معرفة أدناه ، تحتوي على متجهات أعمدة، أو متجهات ذاتية من$phi‪_‬1$ إلى $phi_n$ ، كل منها بحجم $ n \times 1 $ ، وتسمى هذه أيضًا دوال فوريي. وتشكل دوال فوريي أساسًا متعامدًا.

\[\begin{array}{l}\text { where } \underset{n \times n}{\Delta}\Phi=\left[\phi_{1}, \ldots, \phi_{n}\right]=\text { and } \Phi^{T} \Phi=\mathrm{I},\left\langle\phi_{k}, \phi_{k^{\prime}}\right\rangle=\delta_{k k^{\prime}} \\\end{array}\]

المصفوفة $\Lambda$ هي مصفوفة قطرية بقيم ذاتية لابلاسية، و القيم على القطر هي $lambda_1\ $ إلى $lambda_n\ $. ومن التطبيقات التي تمت تسويتها ، تكون هذه القيم عادةً بين النطاق من ‪$‬0‪$‬ إلى ‪$‬2‪$‬. تُعرف هذه أيضًا باسم طيف المخطط. انظر الصيغة أدناه.

\[\begin{array}{c}\text { where } \underset{n \times n}\Lambda=\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{n}\right) \text { and } 0 \leq \lambda_{1} \leq \ldots \leq \lambda_{n}=\lambda_{\max } \leq 2\end{array}\]

يوجد أدناه مثال للتحقق من تحليل القيمة الذاتية. مصفوفة لابلاسيان $Lambda$ مضروبة في المتجهات الذاتية $\phi_k$، وشكل النتيجة‪$‬n \times 1‪$‬ ، والنتيجة هي $lambda_k \phi_k$.

\[\begin{array}{ll}\text { and } \underset{n \times 1}{\Delta \phi_{k}}=\lambda_{k} \phi_{k}, & k=1, \ldots, n \\ & \end{array}\]

الصورة أدناه تبين المتجهات الذاتية لـلبعد الأحادي الإقليدي اللابلاسيي.

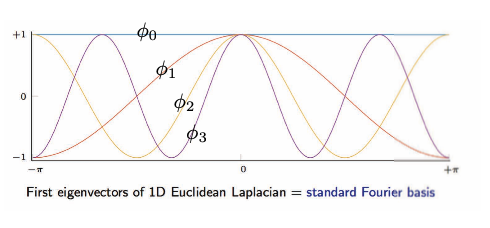
.16 الشكل : المجال الشبكي / الإقليدي: المتجهات الذاتية للبعد الأحادي الإقليدي اللابلاسيي.

بالنسبة لمجال المخطط ، من اليسار إلى اليمين ، هو الأول،الثاني، الثالث،‪…‬ دوال فوريي للمخطط. على سبيل المثال ، يحتوي $phi_1$ على تذبذبات ذات قيم موجبة (حمراء) وسالبة (زرقاء) ، نفس القيم $phi‪‬2$ ، $ \phi‪‬3 $. تعتمد هذه التذبذبات على طوبولوجيا المخطط، والتي تتعلق بهندسة المخططات مثل المجتمعات،المحاور، وما إلى ذلك ، وهي مفيدة للتجميع في المخططات. انظر أدناه.

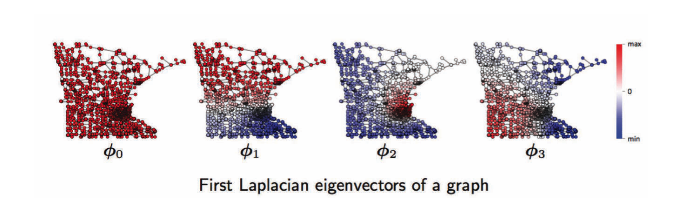
.17 الشكل : مجال المخططات: دوال فوريي للمخططات.

الخطوة الثالثة: تحويل فوريي

\[\begin{aligned} \underset{n \times 1} h &=\sum_{k=1}^{n} \underbrace{\left\langle\phi_{k}, h\right\rangle}_{\mathcal{F}(h)_{k}=\hat{h}_{k}=\phi_{k}^{T} h}\underset{n \times 1}{\phi_{k}} \\ &=\sum_{k=1}^{n} \hat{h}_{k} \phi_{k} \\ &=\underbrace{\Phi \hat{h}}_{ \mathcal{F}^{-1}(\hat{h}) } \end{aligned}\]

** سلاسل فوريي: حلل الدالة $ h $ بدوال فوريي. **

خذ الدالة $ h $ والمسقطة على كل دالة فوريي $\phi_k$، مما ينتج عنه معامل سلاسل فوريي بقيمة $ k $ ، قيمة عددية ، ثم مضروبة في الدالة $phi_k$.

يقوم تحويل فوريي بشكل أساسي بإسقاط دالة $ h $ على دوال فوريي ، والنتيجة هي معاملات سلسلة فوريي.

** تحويل فوريي / معاملات سلاسل فوريي **

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}(h)} &=\Phi^{T} h \\ &=\hat{h} \end{aligned}\]

** تحويل فوريي العكسي **

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}^{-1}(\hat{h})} &=\Phi \hat{h} \\ &=\Phi \Phi^{T} h=h \quad \text { as } \mathcal{F}^{-1} \circ \mathcal{F}=\Phi \Phi^{T}=\mathrm{I} \end{aligned}\]

تحويلات فوريي هي عمليات خطية، محصلة جداء مصفوفة $Phi ^ {T}\ $ بمتجه $ h $.

الخطوة الرابعة: نظرية الإلتفاف

تحويل فوريي لإلتفاف دالتين هو الجداء النقطي لتحويلات فوريي.

\[\begin{aligned} \underset{n \times 1} {w * h} &=\underbrace{\mathcal{F}^{-1}}_{\Phi}(\underbrace{\mathcal{F}(w)}_{\Phi^{T} w=\hat{w}} \odot \underbrace{\mathcal{F}(h)}_{\Phi^{T} h}) \\ &=\underset{n \times n}{\Phi}\left( \underset{n \times 1}{\hat{w}}\odot \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi\left(\underset{n \times n}{\hat{w}(\Lambda)} \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi \hat{w}(\Lambda) \Phi^{T} h \\ &=\hat{w}(\underbrace{\Phi \Lambda \Phi^{T}}_{\Delta}) h \\ &=\underset{n \times n}{\hat{w}(\Delta)} \underset{n \times1}h \\ & \end{aligned}\]

المثال أعلاه هو لإلتفاف $ w $ و $ h $ ، وكلاهما من الشكل ‪$‬n \times 1‪$‬ ، فهو يساوي معكوس تحويل فوريي للجداء النقطي بين تحويل فوريي ل$w$ و $h$. توضح الصيغة أعلاه أنها تساوي أيضًا ضرب المصفوفة $hat{w} (\Delta)$ و $h$.

إن التفاف دالتين على المخطط $ h $ و $ w $ هو أخذ دالة الطيف $ w $ وتطبيقها على لابلاسيان وضربها في $ h $ ، وهذا هو تعريف التفاف الطيف. ومع ذلك ، فإن درجة تعقيد الحساب هي $mathrm{O}\left (n^{2}\right)$ ، بينما $n$ هو عدد العقد في المخطط.

تحديد

لا يؤدي الالتفاف الطيفي مقابل مجال المخطط إلى تغيير الثبات ، مما يعني أنه إذا تم تغييره، فإن شكل الدالة قد يتغير أيضًا، بينما لا يحدث ذلك في المجال الشبكي / الإقليدي.

كتاب موصى به

Spectral graph theory, Fan Chung, (harmonic analysis, graph theory, combinatorial problems, optimization)

---

📝 Bilal Munawar, Alexander Bienstock, Can Cui, Shaoling Chen
Abderrahmane Rahiche
27 Apr 2020