مقدمة للمشفرات الذاتية

تطبيقات المشفرات الذاتية

توليد الصور

هل يمكنك تحديد الوجه المزيف في الشكل 1؟ في الواقع ، تم إنتاج كلاهما بواسطة المولد StyleGan2. على الرغم من أن تفاصيل الوجه واقعية للغاية ، إلا أن الخلفية تبدو غريبة (على اليسار: تشويش ، على اليمين: كائنات مشوهة). هذا لأن الشبكة العصبية تم تدريبها على عينات للوجوه. عندئذ يكون للخلفية تباين أعلى بكثير. هنا ، يحتوي مجمع البيانات على 50 بعدًا تقريبًا ، ,هو نفس عدد درجات الحرية لصورة وجه إنسان.

الشكل 1: وجوه مولّده بواسطة StyleGan2

اختلاف الاستيفاء في فضاء البكسل والفضاء الكامن

الشكل 2: كلب و طير

إذا قمنا بالإستيفاء الخطي (Linear Interpolation) بين صورة الكلب والطير (الشكل 2) في فضاء البكسل ، فسنحصل على تراكب باهت لصورتين في الشكل 3. من أعلى اليسار إلى أسفل اليمين ، ينخفض ​​وزن (أو مدى تأثير) صورة الكلب و يزداد وزن (أو مدى تأثير) صورة الطيور.

الشكل 3: النتائج بعد الإستيفاء الخطي

إذا قمنا بالإستيفاء الخطي لإثنين من تمثيل الفضاء الكامن وقمنا بإدخالهما إلى وحدة فك التشفير ، فسنحصل على تحول من كلب إلى طائر كما في الشكل 4.

الشكل 4: النتائج بعد الإدخال إلى وحده فك التشفير

من الواضح أن الفضاء الكامن أفضل في التقاط بنية الصورة.

أمثلة للتحولات

الشكل 5: تكبير

الشكل 6: إزاحة

الشكل 7: سطوع

الشكل 8: دوران (لاحظ أن الدوران ممكن أن يكون في البعد الثالث)

الصورة فائقة الدقة

يهدف هذا النموذج إلى رفع مستوى الصور وإعادة بناء الوجوه الأصلية.إذا بدأت من اليسار إلى اليمين في الشكل 9 ، ستلاحظ أن العمود الأول هو صورة الإدخال 16 × 16 ، والعمود الثاني هو ما ستحصل عليه من الاستيفاء التكعيبي القياسي (Standard bicubic interpolation) ، والثالث هو الناتج الخارج من الشبكة العصبية ، وعلى اليمين هو الحقيقة الأساسية. (https://github.com/david-gpu/srez)

الشكل 9: إعادة بناء الوجوه الأصلية

من الواضح عند النظر في الصور الموّلده أن هناك تحيزات في بيانات التدريب ، مما يجعل الوجوه المعاد بناؤها غير دقيقة. على سبيل المثال ، تم تصميم الرجل الآسيوي الأيسر العلوي ليبدو أوروبيًا في الناتج بسبب صور التدريب غير المتوازنة. يبدو الوجه المعاد بناؤه للنساء في الجزء اليسار من الأسفل غريبًا بسبب عدم وجود صور التقطت من تلك الزاوية الغريبة في بيانات التدريب.

إعادة رسم الصور

الشكل 10: وضع رقعة رمادية على الوجوه

وضع رقعة رمادية على الوجه كما في الشكل 10 يجعل الصورة بعيدة عن مجمع التدريب. تتم إعادة بناء الوجه في الشكل 11 عن طريق إيجاد أقرب صورة عينة على مجمع التدريب عن طريق تصغير دالة الطاقة.

الشكل 11: الصورة المعاد بناؤها من الشكل 10

تسمية توضيحية للصورة

الشكل 12: مثال على تسمية توضيحية للصورة

تتم الترجمة من وصف النص إلى صورة في الشكل 12 عن طريق استخراج تمثيلات لخصائص النص المرتبطة بالمعلومات المرئية المهمة ثم فك تشفيرها إلى صور.

ماهي المشفرات الذاتية؟

المشفرات الذاتية عبارة عن شبكات عصبية اصطناعية ، يتم تدريبها بطريقة غير خاضعة للإشراف ، وتهدف إلى تعلم التمثيلات المشفرة للبيانات أولاً ثم إنشاء بيانات إدخال (قدر الإمكان) من التمثيلات المشفرة المكتسبة. وبالتالي ، فإن المخرج من المشفر الذاتي هو توقعه للمدخلات.

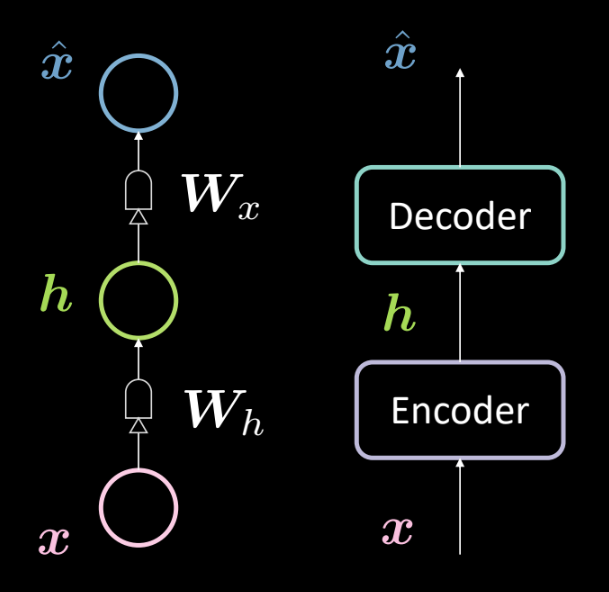
الشكل 13: البناء لمشفر ذاتي بسيط

يوضح الشكل 13 بنية مشفر ذاتي بسيط. كما ذكرنا في السابق ، نبدأ من الأسفل بالمدخل $\ boldsymbol {x}$ الذي يخضع لمشفر (التحويل الأفيني المحدد بواسطة $\ boldsymbol {W_h}$ ، متبوعًا بالضغط). ينتج عن هذا الطبقة المخفية الوسيطة $\ boldsymbol {h}$. هذا يخضع لمفكك التشفير (تحويل أفيني آخر محدد بواسطة $\ boldsymbol {W_x}$ متبوعًا بسحق آخر). ينتج عن هذا الإخراج $\ boldsymbol {\ hat {x}}$ ، وهو توقع النموذج (إعادة بناء المدخلات). وفقًا لتقليدنا في وصف الشبكات العصبية ، نقول أن هذه شبكة عصبية من 3 طبقات.

يمكننا تمثيل الشبكة أعلاه رياضيا باستخدام المعادلات التالية:

We also specify the following dimensionalities:

:ملاحظة من أجل تمثيل PCA ، يمكن أن يكون لدينا أوزان ضيقة (أو أوزان مرتبطة) محددة بواسطة $\ boldsymbol {W_x} \ \ dot {=} \ \ boldsymbol {W_h} ^ \ top$

لماذا نستخدم المشفرات الذاتية

في هذه المرحلة ، قد تتساءل عن الهدف من توقع الإدخال وما هي تطبيقات أجهزة التشفير التلقائية.

التطبيقات الأساسية لوحدة التشفير الذاتي هي اكتشاف عيوب أو تقليل تشويش الصورة. نحن نعلم أن مهمة المشفر الذاتي هي أن تكون قادرة على إعادة بناء البيانات التي تعيش في المجمع للبيانات في حالة وجود مجمع للبيانات كمعطى ، نود أن يكون برنامج التشفير الذاتي قادرًا على إعادة بناء المدخلات الموجودة في هذا المجمع فقط. وبالتالي نحن نقيد النموذج لإعادة بناء الأشياء التي تمت ملاحظتها أثناء التدريب ، وبالتالي سيتم إزالة أي اختلاف موجود في المدخلات الجديدة لأن النموذج سيكون غير حساس لتلك الأنواع من الاضطرابات.

هناك تطبيق آخر لوحدة التشفير التلقائي ألا وهو ضغط الصور. إذا كان لدينا أبعاد وسيطة عددها $d$ أقل من أبعاد الإدخال التي عددها $n$ ، فيمكن استخدام المشفر كضاغط وستعالج التمثيلات المخفية (التمثيلات المشفرة) جميع (أو معظم) المعلومات الموجودة في إدخال ما ولكن ستأخذ مساحة أقل.

خسارة إعادة البناء

دعونا نلقي نظرة الآن على خسائر إعادة البناء التي نستخدمها بشكل عام. يتم إعطاء الخسارة الإجمالية لمجموعة البيانات كمتوسط خسارة لكل عينة ، أي

عندما يكون الإدخال فئويًا (categorical) ، يمكننا استخدام خسارة مقدار الاضطراب البيني (cross-entropy loss) لكل عينة والتي يتم حسابها بواسطة

وعندما تكون المدخلات ذات قيمة حقيقية ، فقد نرغب في استخدام متوسط خسارة الخطأ التربيعي كما يلي

طبقة مخفية غير مكتملة أو مكتملة للغاية

عندما تكون أبعاد الطبقة المخفية $d$ أقل من أبعاد المدخلات $n$ فإننا نقول إنها تحت طبقة مخفية كاملة. وبالمثل ، عندما $d> n$ ، نسميها طبقة مخفية مكتملة. يُظهر الشكل 14 طبقة مخفية غير مكتملة على اليسار وطبقة مخفية مكتملة على اليمين.

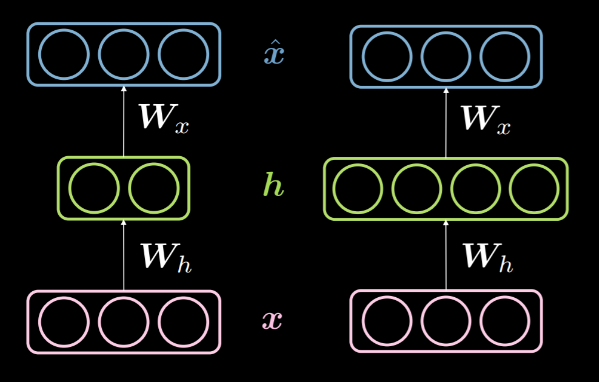
الشكل 14: طبقة مخفية غير مكتملة مقارنة بطبقة مخفية مكتملة للغاية

كما ذكرنا مسبقا ، يمكن استخدام طبقة مخفية غير مكتملة للضغط لأننا نقوم بتشفير المعلومات من الإدخال بأبعاد أقل. من ناحية أخرى ، في طبقة مكتملة للغاية ، نستخدم تشفيرا بأبعاد أعلى من الإدخال. هذا يجعل عملية التحسين الأقصى (optimization) أسهل.

نظرًا لأننا نحاول إعادة بناء المدخلات ، فإن النموذج عرضة لنسخ جميع خصائص المدخلات إلى الطبقة المخفية وتمريرها كإخراج وبالتالي تتصرف بشكل أساسي كدالة هوية . يجب تجنب ذلك لأن هذا يعني أن نموذجنا فشل في تعلم أي شيء. وبالتالي ، نحتاج إلى تطبيق بعض القيود الإضافية من خلال تطبيق عنق الزجاجة للمعلومات. نقوم بذلك عن طريق تقييد التكوينات الممكنة التي يمكن للطبقة المخفية اتخاذها فقط لتلك التكوينات التي يتم رؤيتها أثناء التدريب. يسمح ذلك بإعادة البناء الانتقائي ( الذي يقتصر على مجموعة فرعية من فراغ الإدخال) ويجعل النموذج غير حساس لكل شيء ليس في المجمع.

وتجدر الإشارة إلى أن الطبقة غير المكتملة لا يمكن أن تتصرف كدالة هوية لمجرد أن الطبقة المخفية لا تحتوي على أبعاد كافية لنسخ المدخلات. وبالتالي فإن الطبقة المخفية غير المكتملة أقل احتمالا أن تفرط في التلائم من الطبقة المخفية المكتملة ولكن لا يزال من الممكن أن تفعل ذلك. على سبيل المثال ، إذا كان لدينا وحدة تشفير ووحدة فك تشفير قويتان، يمكن للنموذج ببساطة ربط رقم واحد بكل نقطة بيانات وتعلم التحويل. هناك عدة طرق لتجنب الإفراط في التلائم مثل أساليب التنظيم والأساليب المعمارية وما إلى ذلك.

المشفر الذاتي المزيل للضوضاء

يوضح شكل 15 شكل المجمع للمشفر الذاتي المزيل للضوضاء و الفكرة وراء كيفية عمله

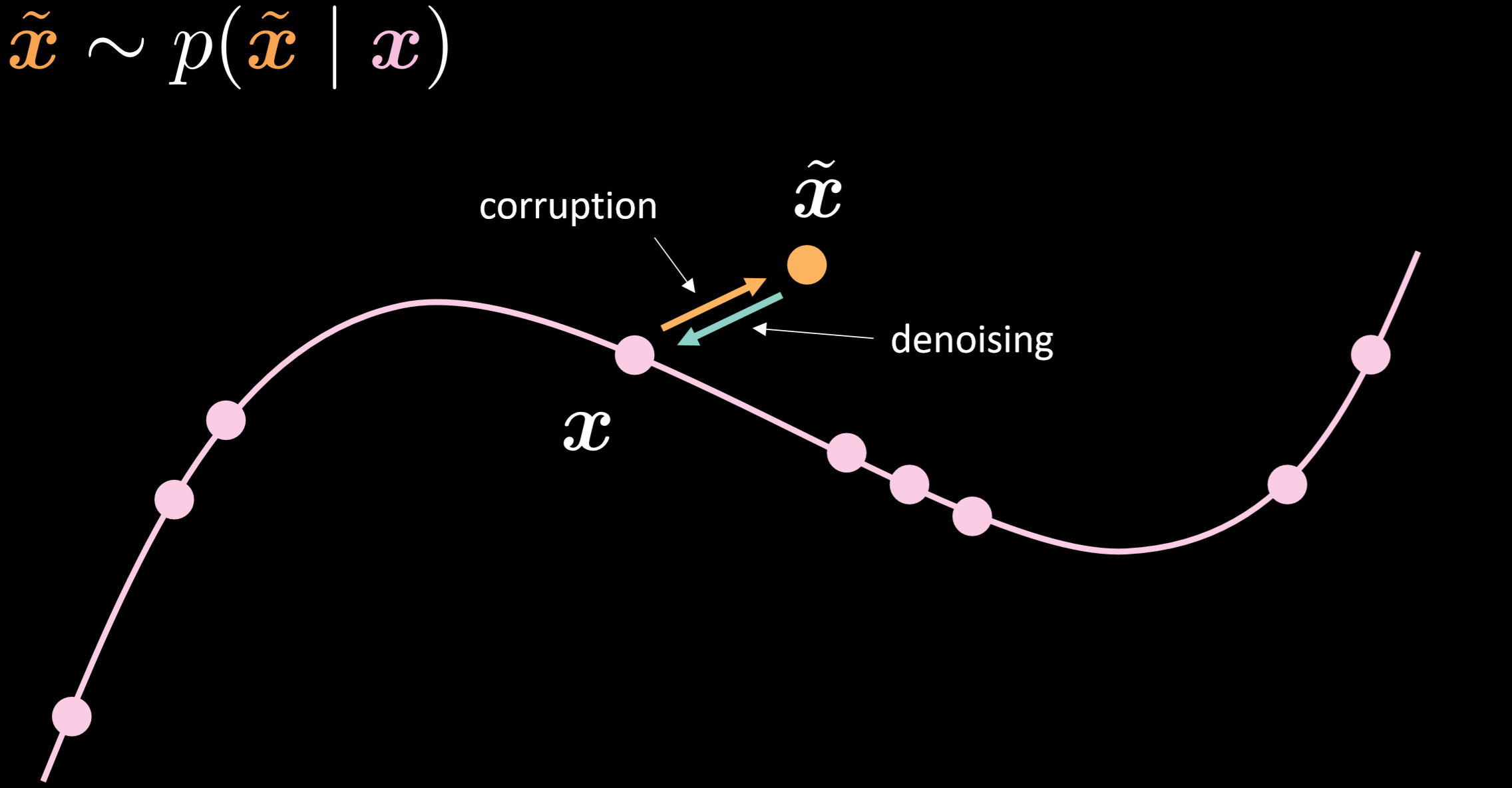
الشكل 15:المشفر الذاتي المزيل للضوضاء

في هذا النموذج ، نفترض أننا نقوم بحقن نفس التوزيع المشوش الذي سنلاحظه في الواقع ، حتى نتمكن من تعلم كيفية التعافي منه بقوة. من خلال مقارنة المدخلات والمخرجات ، يمكننا أن نقول أن النقاط الموجودة بالفعل في المجمع لم تتحرك ، وأن النقاط التي كانت بعيدة عن المجمع تحركت كثيرًا.

يعطي الشكل 16 العلاقة بين بيانات الإدخال وبيانات الإخراج.

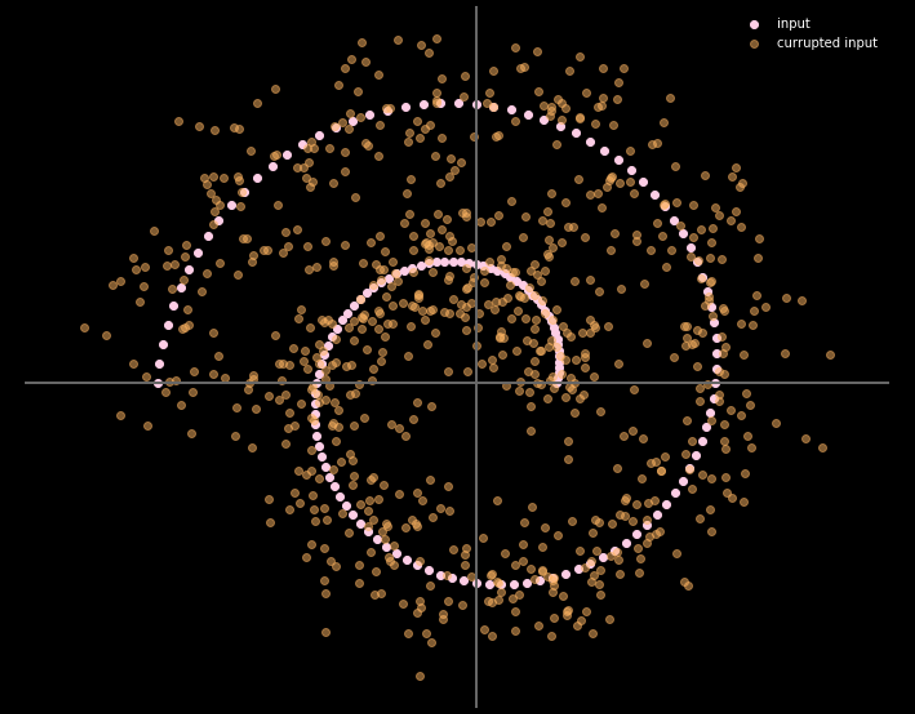
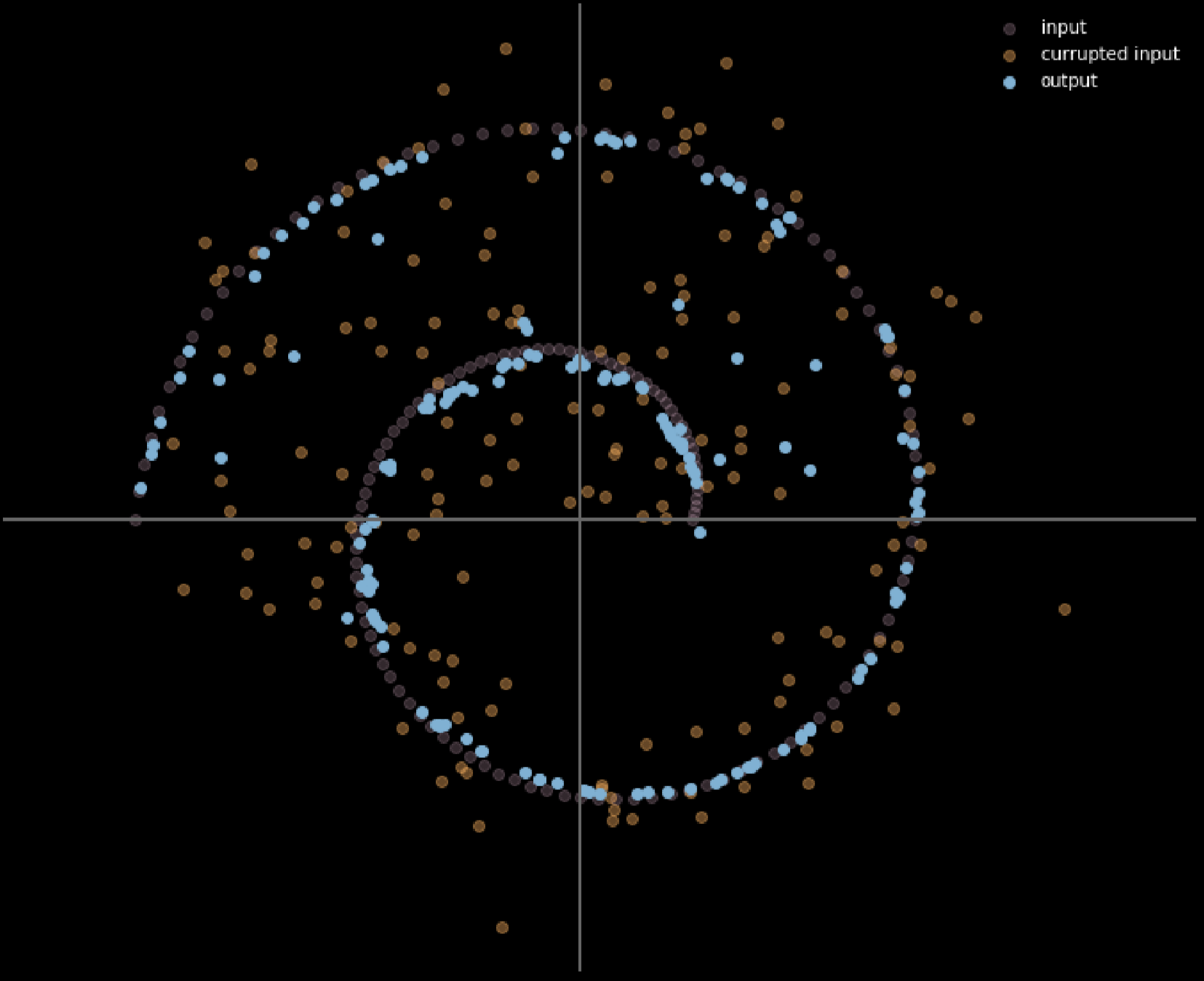
الشكل 16: المدخلات و المخرجات للمشفر الذاتي المزيل للضوضاء

يمكننا أيضًا استخدام ألوان مختلفة لتمثيل مسافة تحرك كل نقطة إدخال ، يوضح الشكل 17 الرسم التخطيطي لذلك.

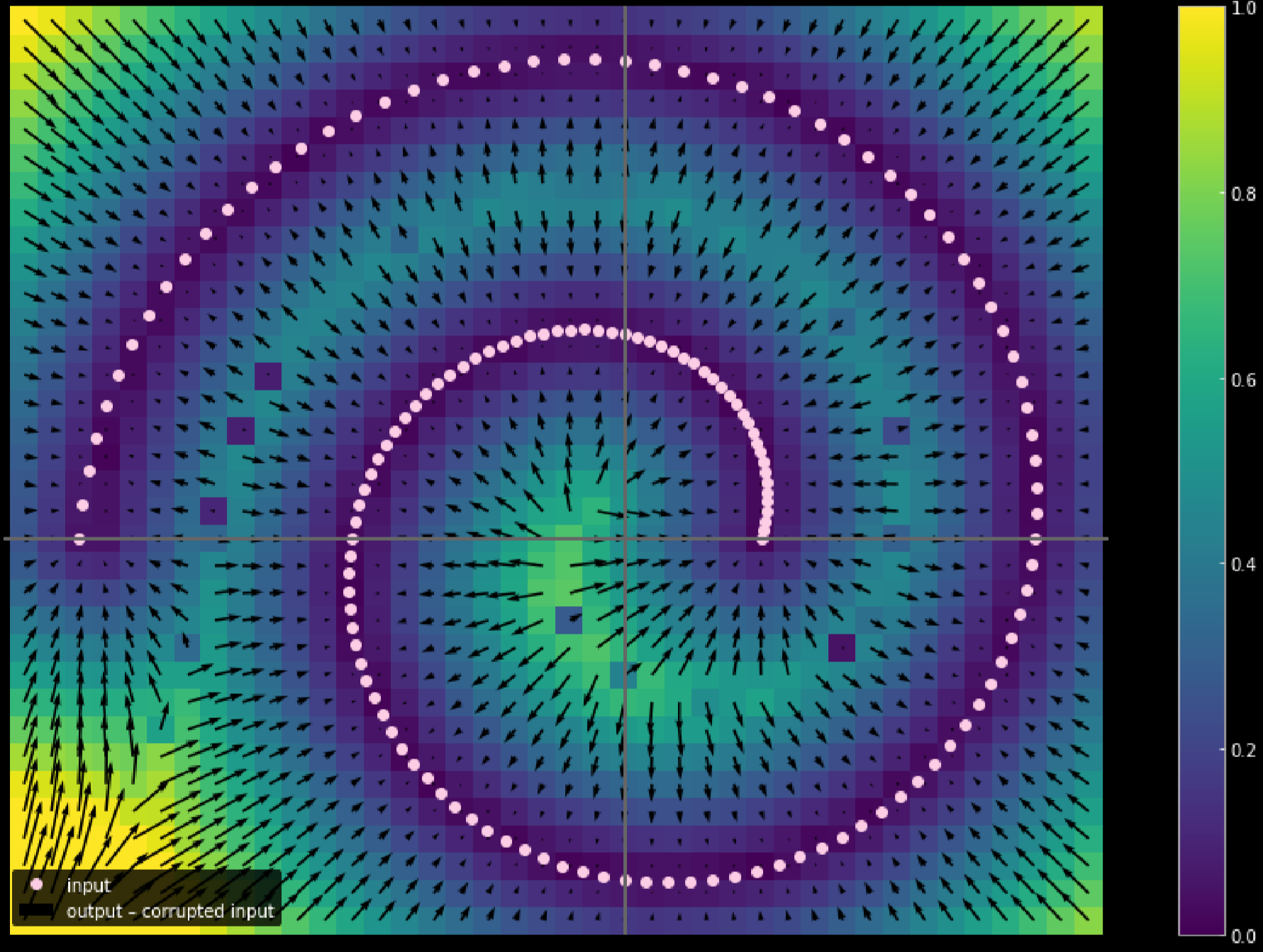
الشكل 17: حساب المسافة المقطوعة للبيانات المدخلة

كلما كان اللون أفتح ، زادت المسافة التي قطعتها النقطة. يمكننا ملاحظة من الرسم التخطيطي أن النقاط الموجودة في الزوايا تتحرك بالقرب من وحدة واحدة ، في حين أن النقاط الموجودة داخل الفرعين لم تتحرك على الإطلاق نظرًا لأنها مربوطة بالفروع العلوية والسفلية أثناء عملية التدريب.

المشفر الذاتي التبايني

يوضح الشكل 18 دالة الخسارة للمشفر الذاتي التابيني و المجمع. Fig.18 shows the loss function of the contractive autoencoder and the manifold.

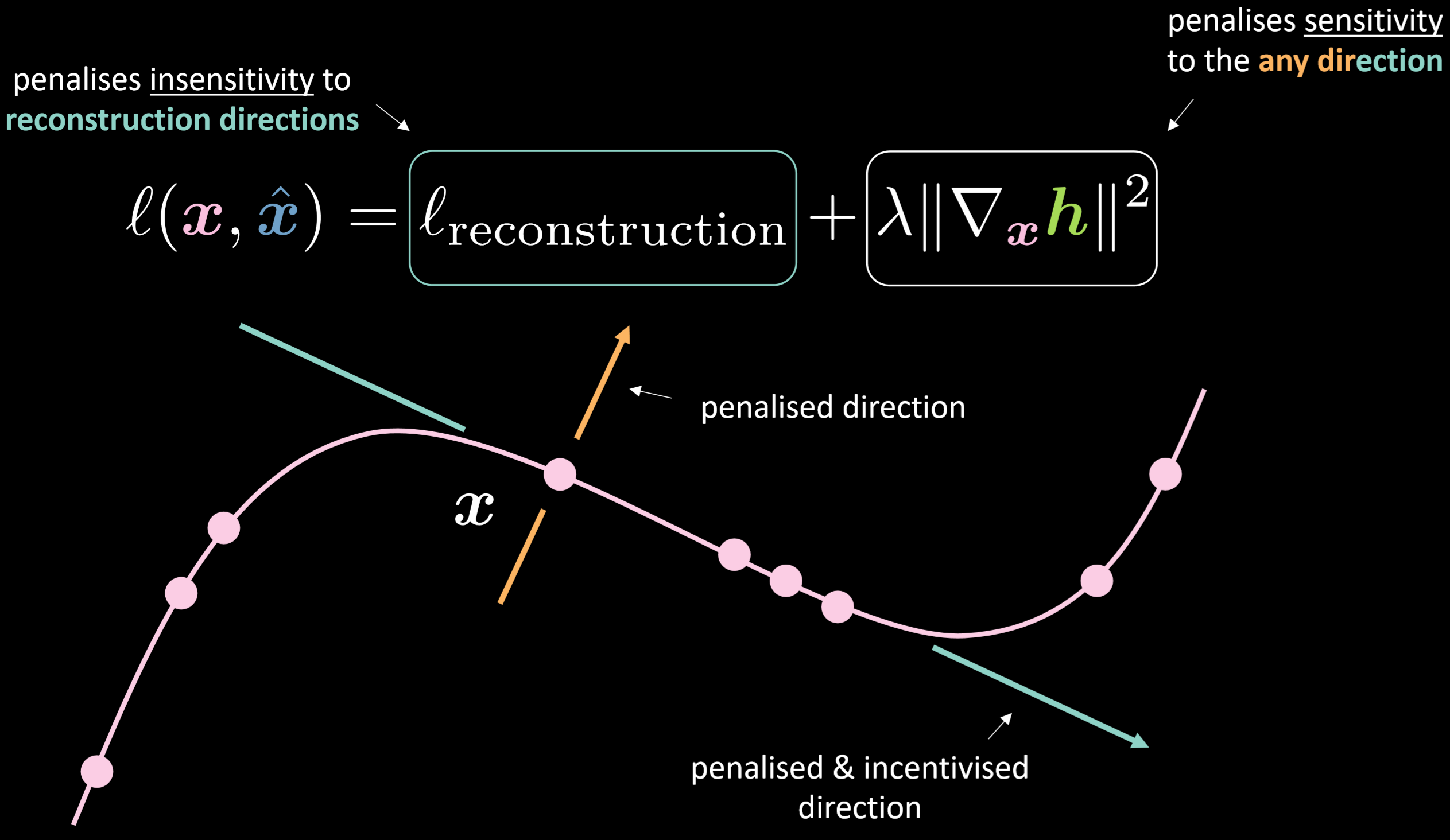
الشكل 18:المشفر الذاتي التبايني

تحتوي دالة الخسارة على جزء إعادة البناء بالإضافة إلى القاعدة التربيعية لتدرج التمثيل الخفي بالنسبة إلى المدخلات. لذلك ، ستقلل الخسارة الإجمالية من تباين الطبقة المخفية نظرًا لتباين المدخلات. وتتمثل الفائدة في جعل النموذج حساسًا لاتجاهات إعادة البناء في حين أنه غير حساس لأي اتجاهات أخرى محتملة.

يوضح الشكل 19 كيفية عمل ذلك المشفر الذاتي بشكل عام.

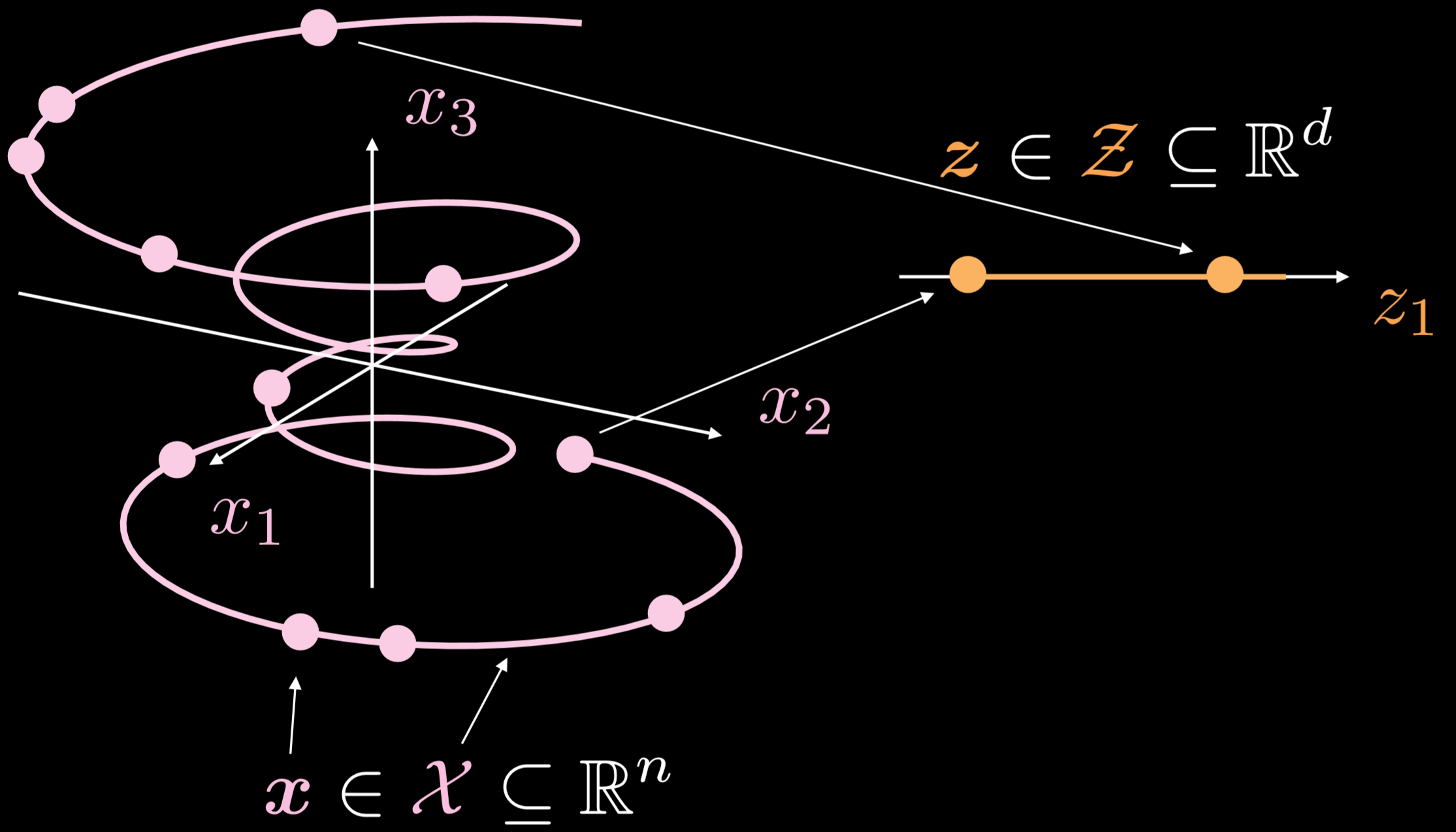
الشكل 19:مشفر ذاتي بسيط

مجمع التدريب هو كائن أحادي البعد يسير في ثلاثة أبعاد. حيث أن $\ boldsymbol {x} \ in \ boldsymbol {X} \ subseteq \ mathbb {R} ^ {n}$ ، الهدف من المشفر الذاتي هو تمديد الخط المتعرج في اتجاه واحد ، حيث أن $\ boldsymbol {z} \ in \ boldsymbol {Z} \ subseteq \ mathbb {R} ^ {d}$. نتيجة لذلك ، سيتم تحويل نقطة من طبقة الإدخال إلى نقطة في الطبقة الكامنة. الآن لدينا الملائمات بين النقاط في فراغ الإدخال والنقاط الموجودة في الفضاء الكامن ولكن ليس لدينا الملائمات بين مناطق فراغ الإدخال ومناطق الفضاء الكامن. بعد ذلك ، سوف نستخدم وحدة فك التشفير لتحويل نقطة من الطبقة الكامنة لإنشاء طبقة إخراج ذات معنى.

تنفيذ المشفر الذاتي - دفتر (notebook)

يمكن العثور على دفتر جوبيتر (Jupyter) [هنا] (https://github.com/Atcold/pytorch-Deep-Learning/blob/master/10-autoencoder.ipynb).

في هذا الدفتر ، سنقوم بتنفيذ برنامج تشفير ذاتي قياسي وجهاز تشفير ذاتي مقلل الضوضاء ثم مقارنة المخرجات خاصتهما.

تعريف بنية نموذج المشفر الذاتي و خسارة إعادة البناء

سنستخدم $28 \times 28& صورة و طبقة مخفية مكونة من 30 بعدًا. التحويل سيتم من $784\to30\to784$. من خلال تطبيق دالة الظل الزائدية على وظيفة المشفر و وظيفة فك التشفير ، يمكننا تقييد نطاق الإخراج بـ$ (- 1 ، 1) $. سيتم استخدام متوسط خسارة الخطأ التربيعي (MSE) كدالة خسارة لهذا النموذج.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

تدريب مشفر ذاتي قياسي

لتدريب برنامج تشفير تلقائي قياسي باستخدام PyTorch ، تحتاج إلى وضع الدالات الخمس التالية في حلقة التدريب:

####: المضي قدمًا

1- إرسال الصورة المدخلة للنموذج عن طريق استدعاء: output = model(img) .
2- حساب الخسارة عن طريق: criterion(output, img.data).

####العودة للخلف:

3- امسح قيمة التدرج للتأكد من أننا لا نراكم القيمة optimizer.zero_grad().
4- الإنتشار الخلفي loss.backward()
5-خذ خطوة تراجع للخلف optimizer.step()

يوضح الشكل 20 إخراج وحدة التشفير القياسية.

الشكل 20المخرج من المشفر الذاتي

تدريب مشفر ذاتي مزيل للضوضاء

يجب إضافة الخطوات التالية للمشفر الذاتي المزيل للضوضاء
1- استدعاء nn.Dropout() حتى نغلق الخلايا العصبية بشكل عشوائي.
do(torch.ones(img.shape)).
2- نخلق قناع للضوضاء: 3- نخلق صور سيئة عن طريق الضرب الحسابي للصور الجيده مع الأقنعة الثنائية img_bad = (img * noise).to(device).

يوضح الشكل 21 إخراج وحدة التشفير القياسية المزيلة للضوضاء.

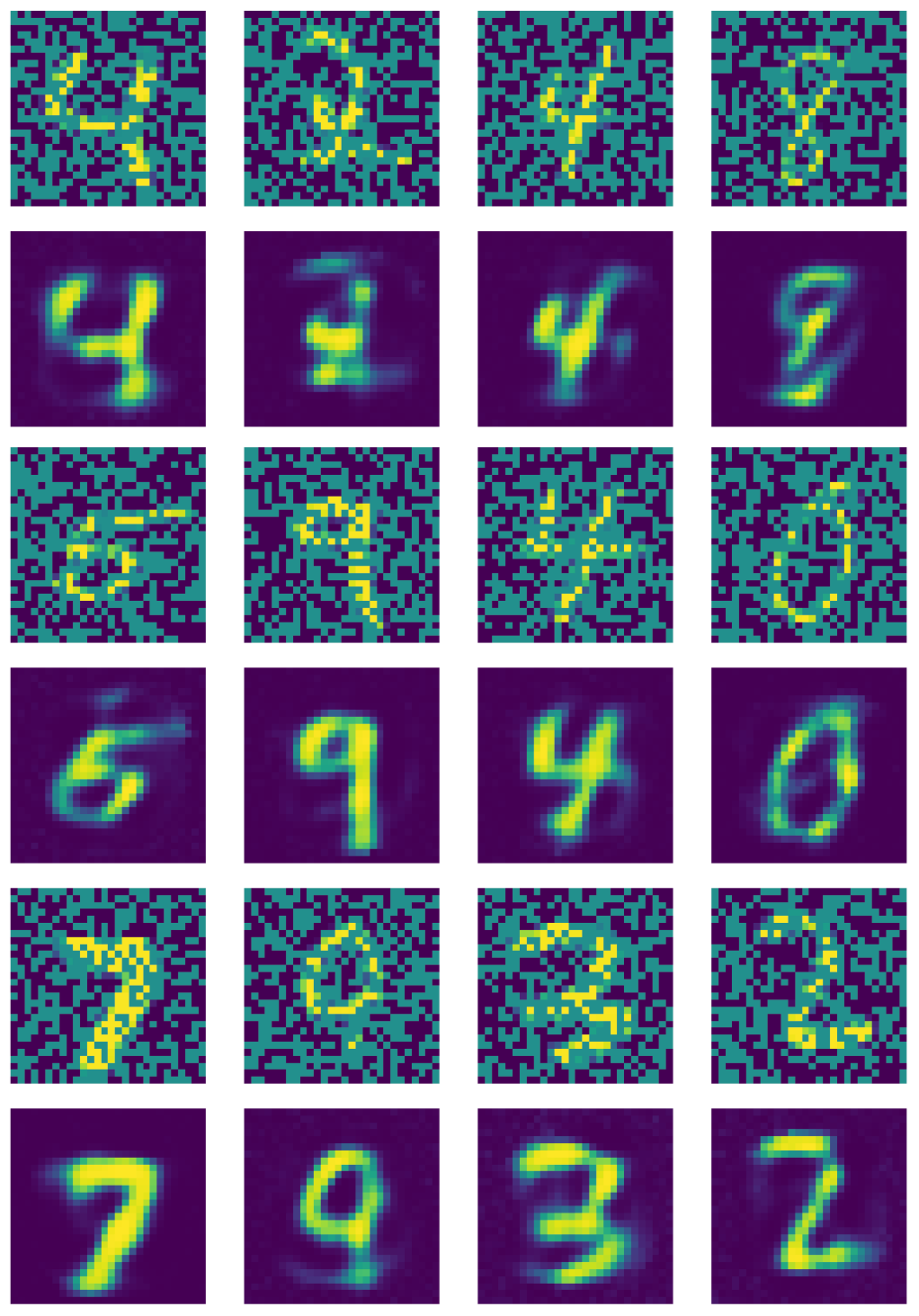
الشكل 21مخرجات المشفر الذاتي المزيل للضوضاء

مقارنة النوى (kernels)

من المهم ملاحظة أنه على الرغم من أن أبعاد الصور المدخلة هي $28 \times 28 = 784$ فإن الطبقة المخفية ذات البعد 500 لا تزال طبقة مكتملة للغاية بسبب عدد النقاط السوداء في الصورة. فيما يلي أمثلة على النوى المستخدم في المشفر الذاتي القياسي الغير الكامل المدرب. من الواضح أن وحدات البكسل (النقاط) في المنطقة التي يوجد بها الرقم تشير إلى اكتشاف نوع من الأنماط ، في حين أن وحدات البكسل الموجودة خارج هذه المنطقة عشوائية بشكل أساسي. يشير هذا إلى أن المشفر الذاتي القياسي لا يهتم بالبكسل خارج المنطقة التي يوجد بها الرقم.

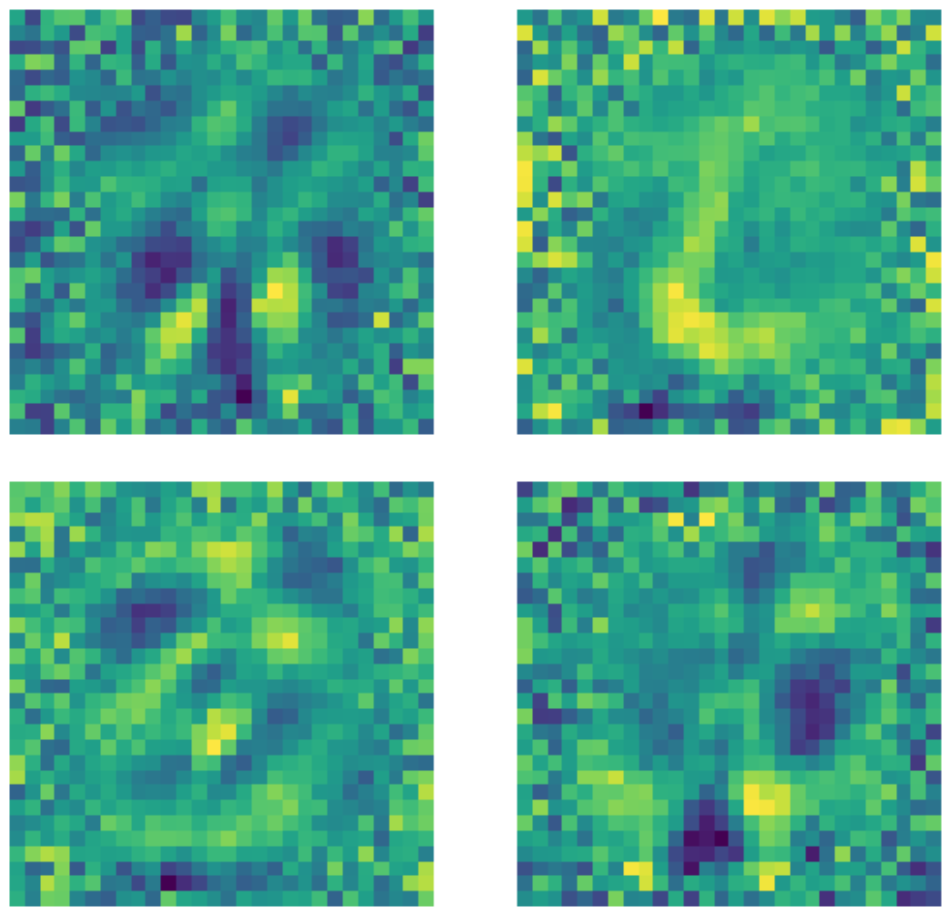
الشكل 22: نوى المشفر الذاتي القياسي

من ناحية أخرى ، عندما يتم تغذية نفس البيانات إلى مشفر ذاتي مقلل للضوضاء حيث يتم تطبيق قناع غلق الخلايا العصبية على كل صورة قبل ملائمة النموذج ، يحدث شيء مختلف. كل نواة تتعلم نمطًا ما تقوم بتعيين وحدات البكسل خارج المنطقة حيث يوجد الرقم بقيمة ثابتة. نظرًا لتطبيق قناع الغلق على الصور ، فإن النموذج يهتم الآن بالبكسل خارج منطقة الرقم.

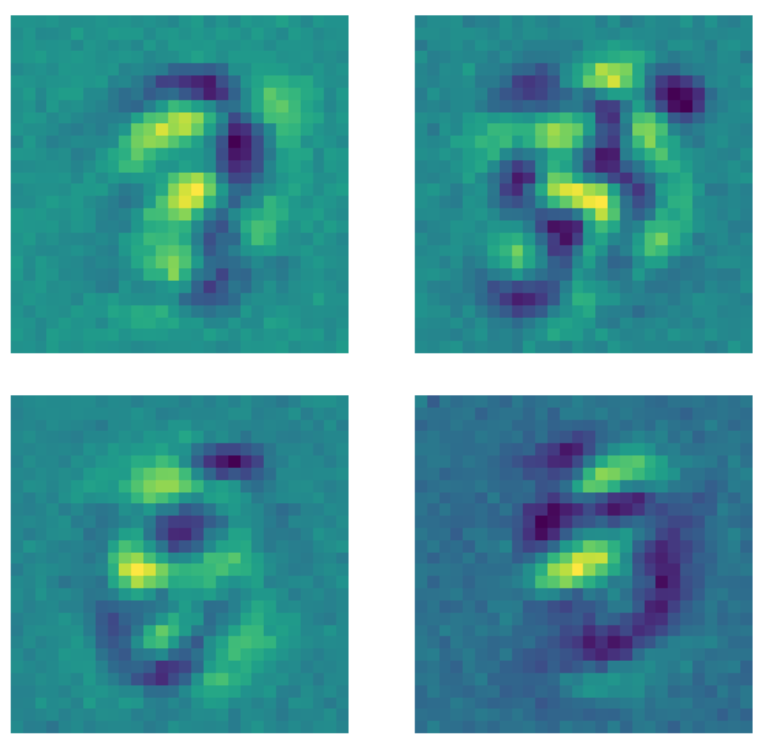
الشكل 23: نوى المشفر الذاتي المقلل للضوضاء.

بالمقارنة مع أحدث ما توصلت إليه التكنولوجيا ، فإن برنامج المشفر الذاتي لدينا يعمل بشكل أفضل !! يمكنك ان ترى النتائج اسفل.

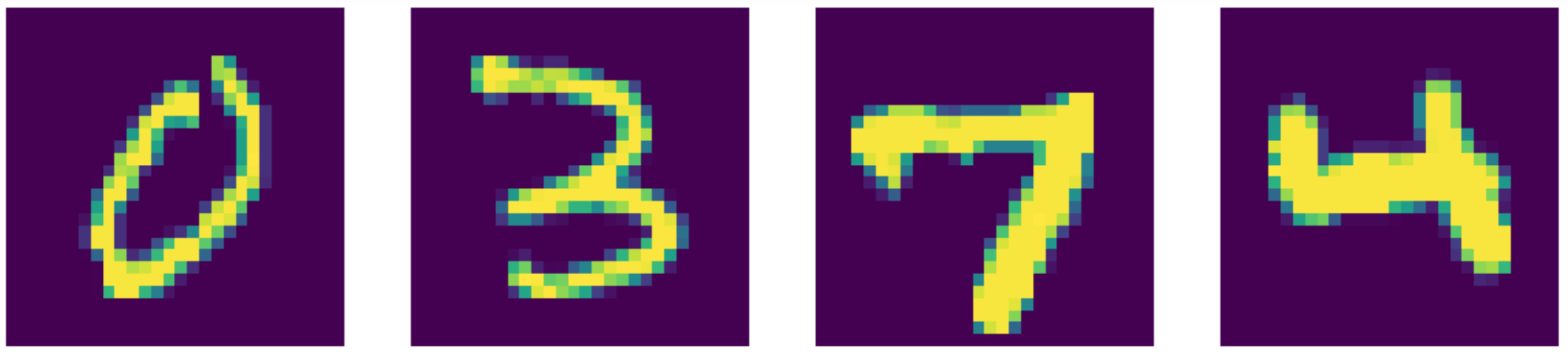
الشكل 24: بيانات الإدخال (MNIST أرقام).

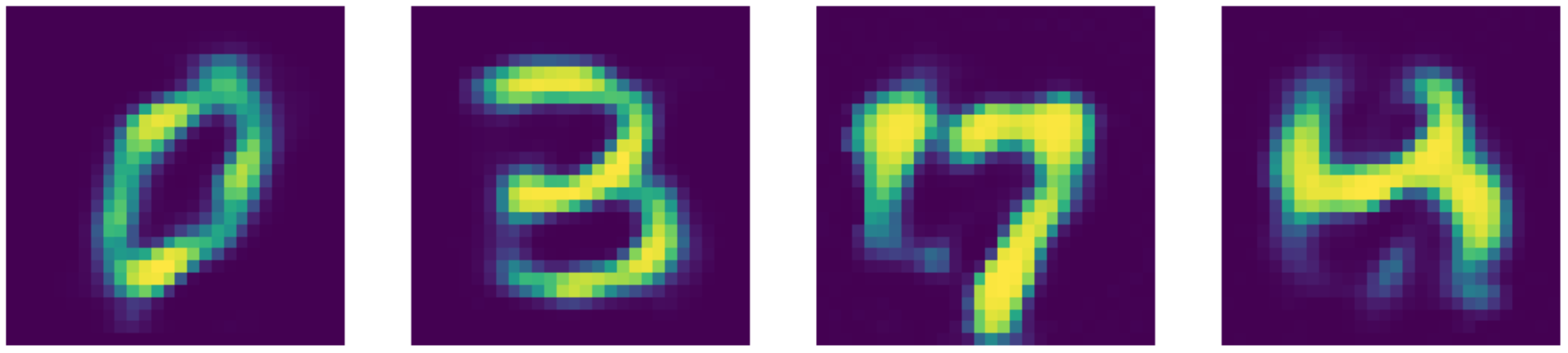
الشكل 25: إعادة البناء للمشفر الذاتي المقلل للضوضاء.

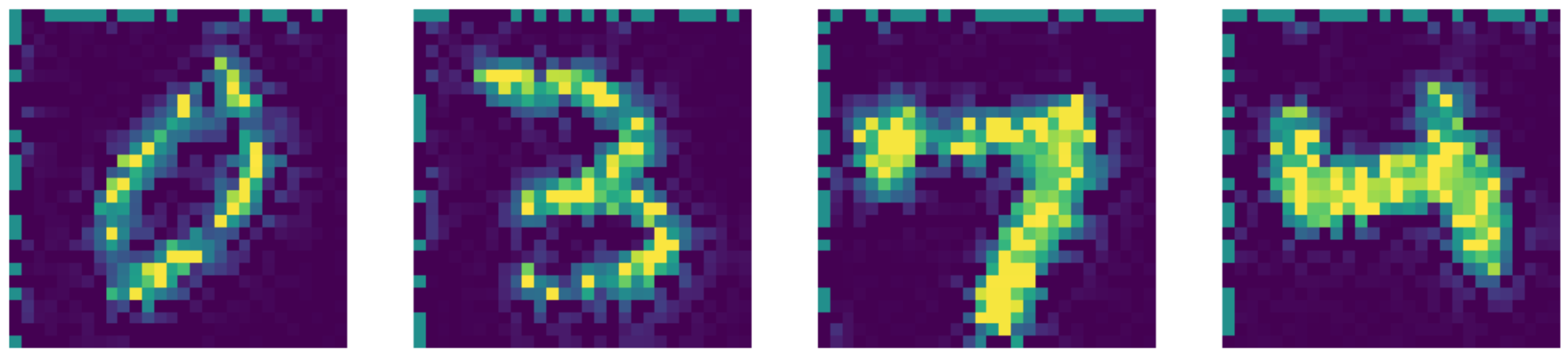
الشكل 26: Telea المخرج لإعادة رسم.

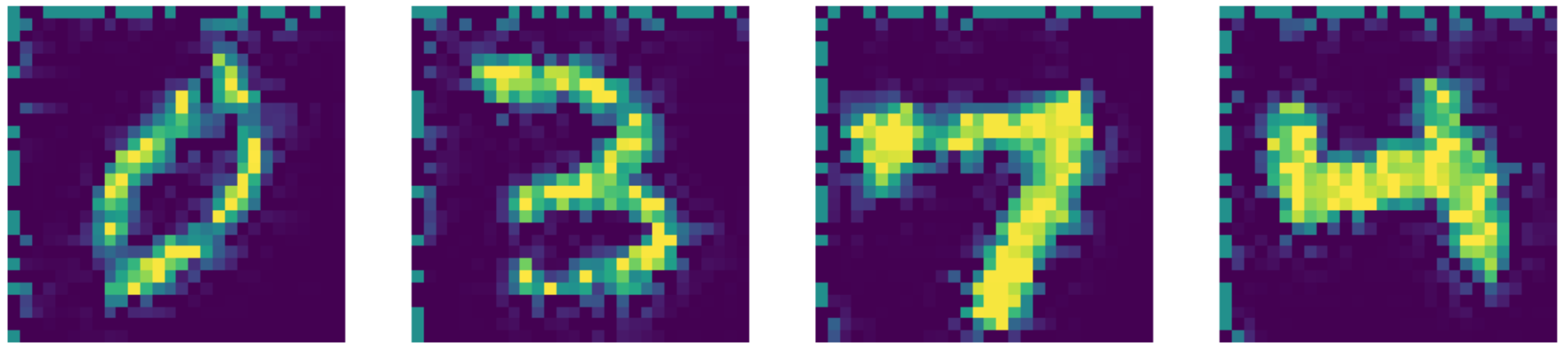
الشكل 27: Navier-Stokes المخرج لإعادة رسم.