بالتفاصيل و الأمثلة SSL و EBM

التعلم بالإشراف الذاتي

يشمل التعلم بالإشراف الذاتي (Self Supervised Learning, SSL) كلاً من التعلم بلإشراف و التعلم بدون إشراف. الهدف من مهمة SSL هو تعلم تمثيل جيد للمدخلات بحيث يمكن استخدامه لاحقًا للمهام الخاضعة للإشراف. باستخدام SSL ، يتم تدريب النموذج على تنبؤ جزء واحد من البيانات في ضوء وجود أجزاء أخرى من البيانات. على سبيل المثال ، تم تدريب BERT باستخدام تقنيات SSL وقد أظهر برنامج المشفر التلقائي لإزالة الضوضاء (DAE) بشكل خاص أفضل النتائج في معالجة اللغة الطبيعية (NLP).

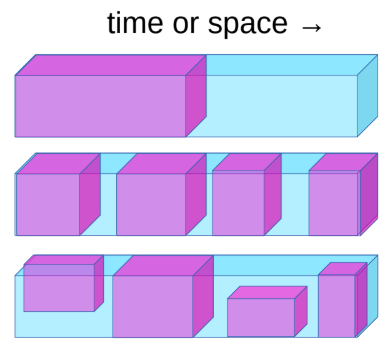
الشكل 1: التعلم بالإشراف الذاتي

يمكن تعريف مهمة التعلم بالإشراف الذاتي على النحو التالي:

• توقع المستقبل من الماضي.
• توقع المخفي من المرئي.
• توقع أي أجزاء محجوبة من البيانات من جميع الأجزاء الأخرى المتاحة.

على سبيل المثال ، إذا تم تدريب النظام على تنبؤ الإطار التالي عند تحريك الكاميرا ، فسيتعلم النظام ضمنيًا على العمق واختلاف المنظر. سيؤدي ذلك إلى إجبار النظام على تعلم أن الأشياء المحجوبة عن رؤيته لا تختفي بل تستمر في الوجود و تعلم التمييز بين الكائنات الحية وغير الحية والخلفية. يمكن أن ينتهي به الأمر أيضًا إلى التعرف على الفيزياء البديهية مثل الجاذبية.

تقوم أحدث أنظمة البرمجة اللغوية العصبية (BERT) الحديثة بتدريب شبكة عصبية عملاقة مسبقًا على مهمة SSL. تقوم بإزالة بعض الكلمات من جملة وتجعل النظام يتنبأ بالكلمات المفقودة. لقد كان هذا ناجحًا جدًا. تم أيضًا تجربة أفكار مماثلة في مجال رؤية الكمبيوتر. كما هو موضح في الصورة أدناه ، يمكنك التقاط صورة وإزالة جزء من الصورة وتدريب النموذج على التنبؤ بالجزء المفقود.

الشكل 2: نتائج في مجال رؤية الكمبيوتر

على الرغم من أن النماذج يمكن أن تملأ المساحة المفقودة ، إلا أنها لم تشارك نفس مستوى النجاح مثل أنظمة البرمجة اللغوية العصبية. إذا كنت ستأخذ التمثيلات الداخلية التي تم إنشاؤها بواسطة هذه النماذج ، كمدخلات لنظام رؤية الكمبيوتر ، فلن تتمكن من التغلب على نموذج تم تدريبه مسبقًا بطريقة الإشراف على ImageNet. الفرق هنا هو أن البرمجة اللغوية العصبية منفصلة بينما الصور مستمرة. الفرق في النجاح هو أننا في المجال المنفصل نعرف كيفية تمثيل عدم اليقين حيث أننا نستطيع استخدام دالة softmax كبير على المخرجات المحتملة ،لكن في المجال المستمر لا نستطيع فعلا ذلك.

يحتاج نظام الذكاء الإصطناعي إلى أن يكون قادرًا على التنبؤ بنتائج عمله على البيئة المحيطة وعلى نفسه لاتخاذ قرارات ذكية. نظرًا لأن العالم ليس حتميًا تمامًا ولا توجد قوة حسابية كافية في أي آلة / دماغ بشري لتفسير كل الاحتمالات ، نحتاج إلى تعليم أنظمة الذكاء الاصطناعي للتنبؤ في حالة عدم اليقين عند العمل مع فضائات عالية الأبعاد. يمكن أن تكون النماذج القائمة على الطاقة (ُEnergy Based Models, EBMs) مفيدة للغاية لهذا الغرض.

ستؤدي الشبكة العصبية التي تم تدريبها باستخدام المربعات الصغرى للتنبؤ بالإطار التالي لمقطع فيديو في شكل صور ضبابية لأن النموذج لا يمكنه التنبؤ بالمستقبل بالضبط ، لذلك يتعلم متوسط ​​جميع احتمالات الإطار التالي من بيانات التدريب لتقليل الخسارة.

النماذج الكامنة القائمة على الطاقة المتغيرة كحل لتنبؤ الإطار التالي:

على عكس الانحدار الخطي ، تأخذ النماذج القائمة على الطاقة المتغيرة الكامنة ما نعرفه عن العالم بالإضافة إلى المتغير الكامن الذي يعطينا معلومات حول ما حدث في الواقع. يمكن استخدام مزيج من هاتين المعلومتين لعمل تنبؤ قريب مما يحدث بالفعل.

يمكن اعتبار هذه النماذج على أنها أنظمة تقيم التوافق بين المدخلات $x$ والمخرجات الفعلية $y$ اعتمادًا على التنبؤ باستخدام المتغير الكامن الذي يقلل من طاقة النظام. هي تلاحظ الإدخال $x$ وتنتج تنبؤات محتملة $\bar{y}$ لتوليفات مختلفة من المتغيرات $x$ والمتغيرات الكامنة $z$ وتختار التوليفة التي تقلل من الطاقة ، وخطأ التنبؤ ، للنظام.

اعتمادًا على المتغير الكامن الذي نسحبه ، يمكننا أن ننتهي بكل التوقعات الممكنة. يمكن اعتبار المتغير الكامن على أنه جزء من المعلومات المهمة حول الناتج $y$ غير موجود في الإدخال $x$.

يمكن أن تكون الدال ذات القيمة العددية المعتمدة على الطاقة على وجهين:

1. مشروطة $F(x, y)$ - تقوم بقياس مدى التوافق بين $x$ , $y$
2. غير مشروطة $F(y)$ - تقوم بقياس مدي التوافق بين مكونات $y$

تدريب نموذج قائم على الطاقة

هناك فئتان من نماذج التعلم لتدريب نموذج قائم على الطاقة لتحديد قيمة $ F (x، y) $.

1. ** طرق التباين: ** اضغط لأسفل $ F (x [i]، y [i]) $ ، وادفع لأعلى في النقاط الأخرى $ F (x [i]، y ‘) $
2. ** الأساليب المعمارية: ** بناء $ F (x، y) $ بحيث يكون حجم المناطق منخفضة الطاقة محدودًا أو يتم تقليله عن طريق أساليب التنظيم

هناك سبع استراتيجيات لتشكيل دالة الطاقة. تختلف طرق التباين في طريقة اختيار النقاط للدفع لأعلى. بينما تختلف الأساليب المعمارية في الطريقة التي تحد من سعة المعلومات الخاصة بالشفرة.

مثال على طريقة التباين هو تعلم الاحتمال الأقصى (Maximum Likelihood Learning). يمكن تفسير الطاقة على أنها كثافة لوغاريتمية سالبة غير مسوّاه. يمنحنا توزيع Gibbs الاحتمالي الاحتمال الأقصى لـ $ y $ مقابل $ x $. يمكن صياغتها على النحو التالي:

أقصى احتمال يحاول جعل البسط كبيرًا والمقام صغيرًا لزيادة الاحتمالية. هذا يعادل تقليص $-\log(P(Y \mid W))$ كما هو موضح أدناه

حساب الانحدار لخسارة احتمالية اللوغاريتم السلبي لعينة واحدة من Y يكون كالتالي:

في الانحدار أعلاه ، يتم حساب المصطلح الأول التدرج عند نقطة البيانات $ Y $ والمصطلح الثاني من التدرج القيمة المتوقعة لتدرج الطاقة على كل نقاط بيانات $ Y $ . ومن ثم ، عندما نقوم بالانحدار التدريجي ، فإن المصطلح الأول يحاول تقليل الطاقة المعطاة لنقطة البيانات $ Y $ ويحاول المصطلح الثاني زيادة الطاقة المعطاة لجميع نقاط $Y$ الأخرى.

يعد انحدار دالة الطاقة بشكل عام معقدًا للغاية ، وبالتالي فإن حساب التكامل أو تقديره أو تقريبه هو حالة مثيرة للاهتمام للغاية لأنه من الصعب حلها في معظم الحالات.

نموذج المتغير الكامن القائم على الطاقة

الميزة الرئيسية لنماذج المتغير الكامن هي أنها تسمح بتنبؤات متعددة من خلال المتغير الكامن. نظرًا لأن $ z $ يتغير داخل مجموعة ، فإن $ y $ يتغير داخل مجموعة التنبؤات المحتملة. تتضمن بعض الأمثلة ما يلي:

1. K-means وسائل عدة
2. النمذجة المتناثرة (Sparse Modeling)
3. [GLO] (https://arxiv.org/abs/1707.05776)

يمكن أن تكون من نوعين:

1. النماذج الشرطية حيث يعتمد $ y $ على $ x $
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. النماذج غير المشروطة التي لها دالة طاقة ذات قيمة قياسية ، $ F (y) $ التي تقيس التوافق بين مكونات $ y $
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

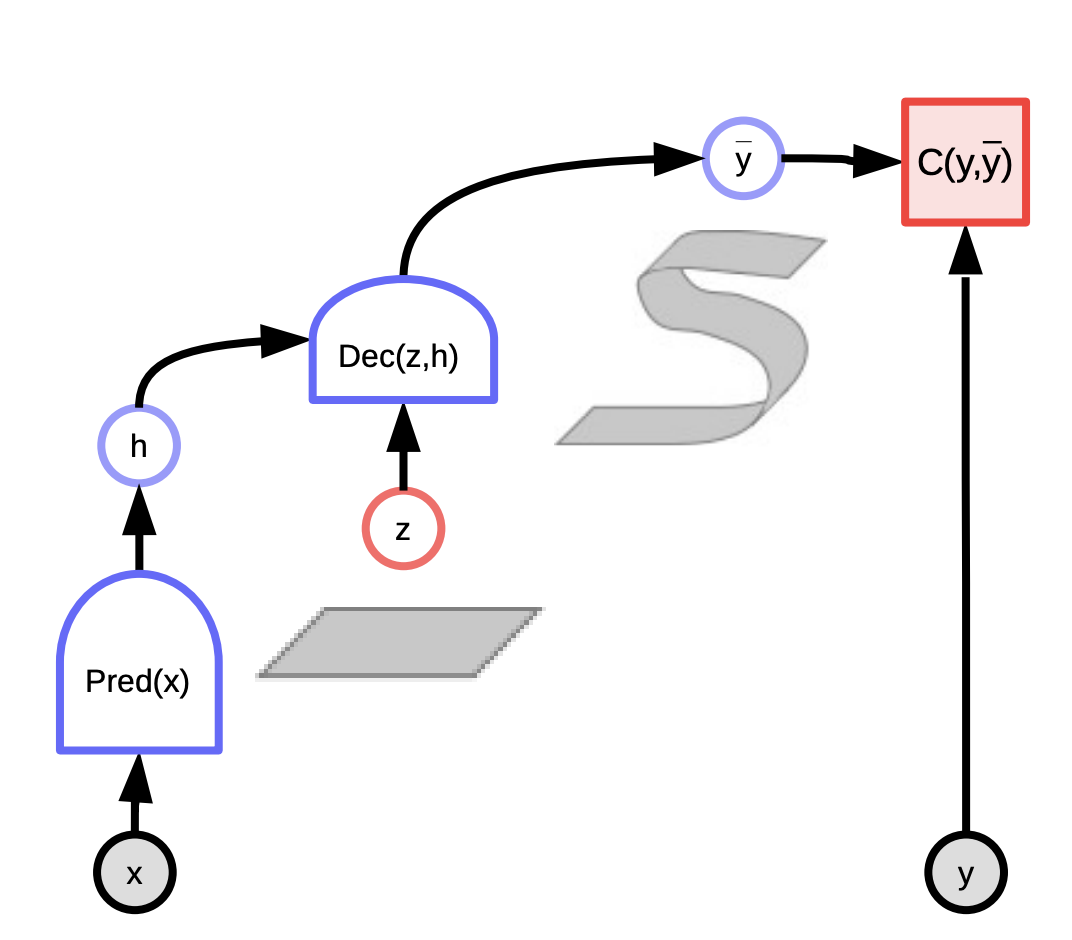
الشكل 3: المتغير الكامن القائم على الطاقة

مثال على نموذج المتغير الكامن EBM: k-means

K-mean هي خوارزمية تجميع بسيطة يمكن اعتبارها أيضًا نموذجًا قائمًا على الطاقة حيث نحاول نمذجة التوزيع على $ y $. دالة الطاقة هي $ E (y، z) = \ Vert y-Wz \ Vert ^ 2 $ حيث $ z $ متجه ساخن بقيمة $ 1 $. طريقة الوسائل العدة (k-mean) هو خوارزمية تجميع بسيطة يمكن اعتبارها أيضا نموذجًا قائمًا على الطاقة حينما نحاول نمذجة التوزيع على المتغير $y$. دالة الطاقة هي $$ُE(y,z) = \Vert y-Wz \Vert^2 حيث أن $z$ هو متجه ساخن واحد (1-hot vector)

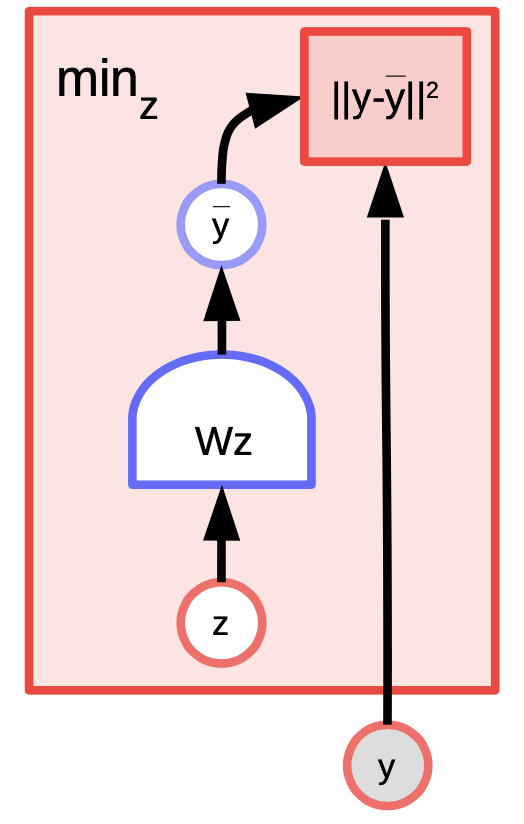
الشكل 4: مثال للوسائل العدة

بالنظر إلى قيمة $ y $ و $ k $ ، يمكننا عمل استنتاج من خلال معرفة أي من الأعمدة المحتملة من $w$ ذات العدد $k$ يقلل من خطأ إعادة البناء أو دالة الطاقة. لتدريب الخوارزمية ، يمكننا اعتماد نهج حيث يمكننا العثور على $ z $ لاختيار عمود $ W $ الأقرب إلى $ y $ ثم محاولة الاقتراب من خلال اتخاذ خطوة انحدار وتكرار العملية. مع ذلك ، فإن انحدار الكتل التدريجي (Block gradient descent) يعمل بشكل أفضل وأسرع.

في الرسم أدناه يمكننا أن نرى نقاط البيانات على طول اللولب الوردي. تتوافق النقط السوداء المحيطة بهذا الخط مع الآبار التربيعية حول كل نموذج أولي لـ $ W $.

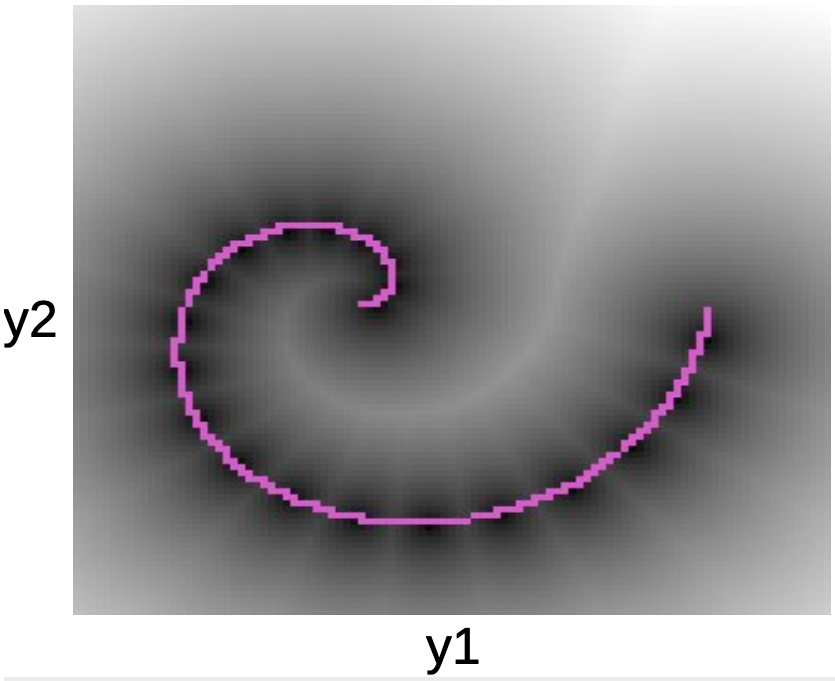
الشكل 5: الرسم اللولبي

بمجرد أن نتعلم دالة الطاقة ، يمكننا البدء في معالجة أسئلة مثل:

1. بالنظر إلى النقطة $ y_1 $ ، هل يمكننا توقع $ y_2 $؟
2. بالنظر إلى $ y $ ، هل يمكننا إيجاد أقرب نقطة لها في مجمع البيانات؟

تنتمي الوسائل العدة k-means إلى الأساليب المعمارية (على عكس طرق التباين). ومن ثم فإننا لا نرفع الطاقة لأعلى في أي مكان ، كل ما نفعله هو دفع الطاقة إلى الأسفل في مناطق معينة. هناك عيب واحد هو أنه بمجرد تحديد قيمة $ k $ ، يمكن أن يكون هناك فقط عدد $ k $ من النقاط التي تحتوي على $ 0 $ من الطاقة ، وكل نقطة أخرى سيكون لها طاقة أعلى تنمو بشكل تربيعي كلما ابتعدنا عنهم.

طرق التباين

وفقًا للدكتور Yann LeCun ، سيستخدم الجميع طرقًا معمارية في مرحلة ما ، ولكن في هذه اللحظة ، فإن أساليب التباين تعمل جيدًا مع الصور. ضع في اعتبارك الشكل أدناه الذي يوضح لنا بعض نقاط البيانات وخطوط سطح الطاقة. من الناحية المثالية ، نريد أن يكون لسطح الطاقة أقل طاقة في مجمع البيانات. ومن ثم فإن ما نود فعله هو خفض الطاقة (بمعنى آخر قيمة $ F (x، y) $) حول مثال التدريب ، ولكن هذا وحده قد لا يكون كافياً. ومن ثم نرفعها أيضًا مقابل $ y $ في المنطقة التي يجب أن تحتوي على طاقة عالية ولكن بها طاقة منخفضة.

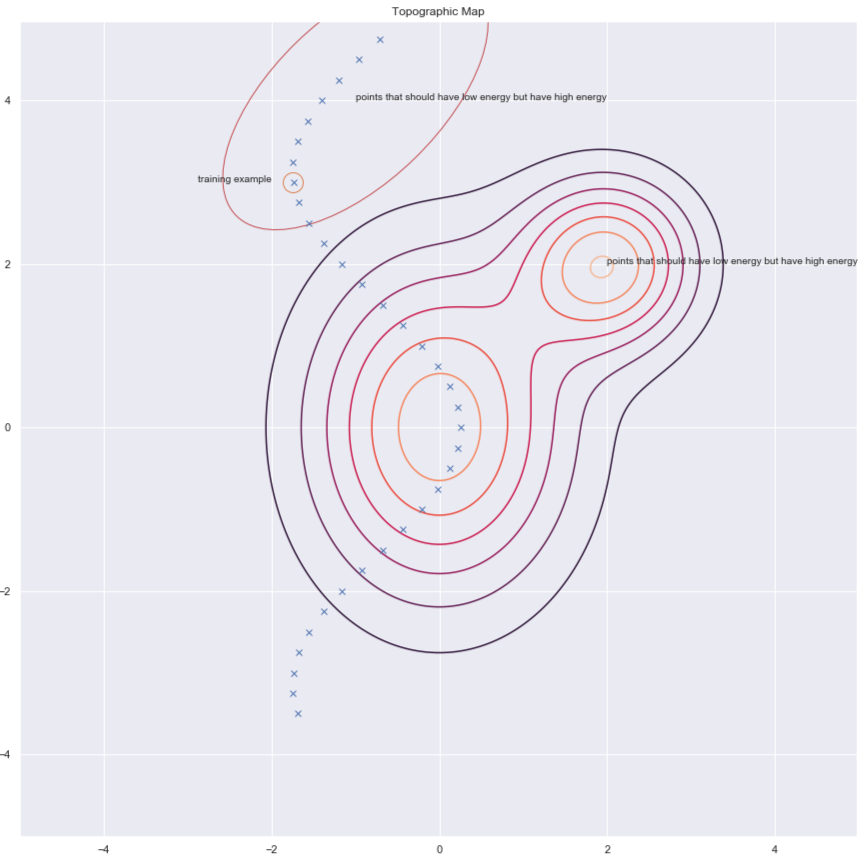
الشكل 6: طرق التباين

هناك عدة طرق للعثور على هؤلاء المرشحين $ y $ الذين نريد زيادة الطاقة من أجلهم. بعض الأمثلة هي:

1. Denoising Autoencoder المشفر التلقائي المقلل للضوضاء
2. الاختلاف التبايني Contrastive Divergence
3. Monte Carlo مونتي كارلو
4. سلسلة ماركوف مونتي كارلو Markov Monte Carlo
5. مونتي كارلو الهاميلتوني Hamiltonian Monte carlo

سنناقش بإيجاز المشفر التلقائي المقلل للضوضاء والاختلاف التبايني.

المشفر التلقائي المقلل للضوضاء (DAE)

إحدى طرق إيجاد $ y $ لأجل زيادة الطاقة لها هي عن طريق احداث اضطراب عشوائي لمثال التدريب كما هو موضح بواسطة الأسهم الخضراء في الرسم أدناه.

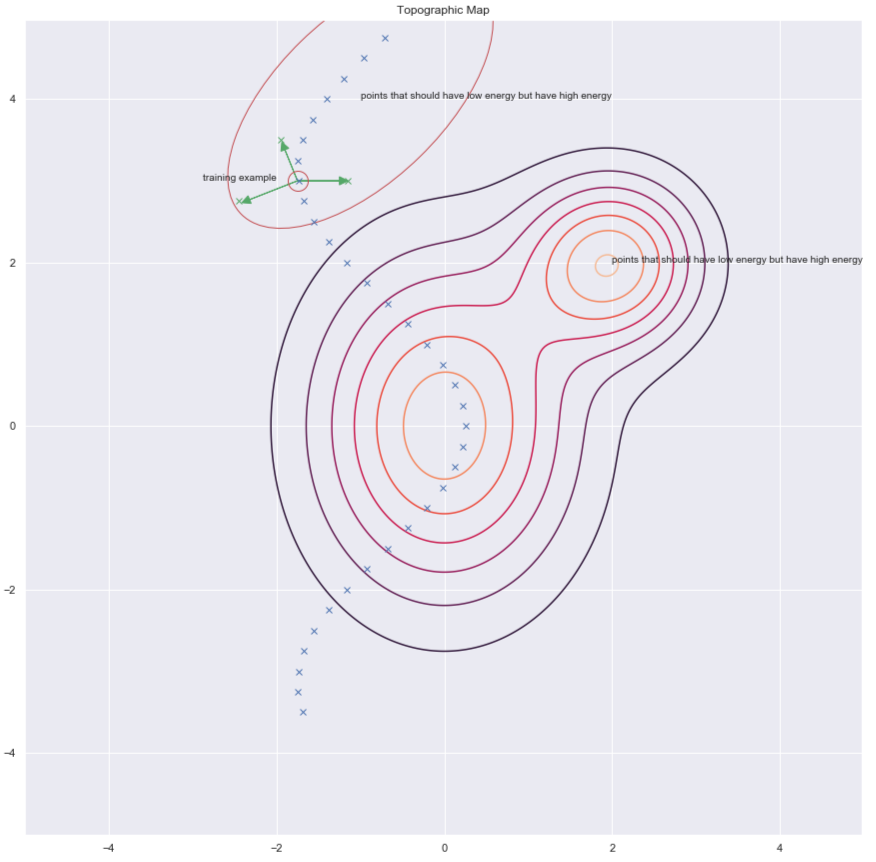
الشكل 7: الخريطة الطبوغرافية

مجرد أن يكون لدينا نقطة بيانات تالفة ، يمكننا دفع الطاقة هنا. إذا قمنا بذلك عدة مرات بشكل كافٍ لجميع نقاط البيانات ، فإن عينة الطاقة سوف تلتف حول أمثلة التدريب. توضح الحبكة التالية كيف يتم التدريب.

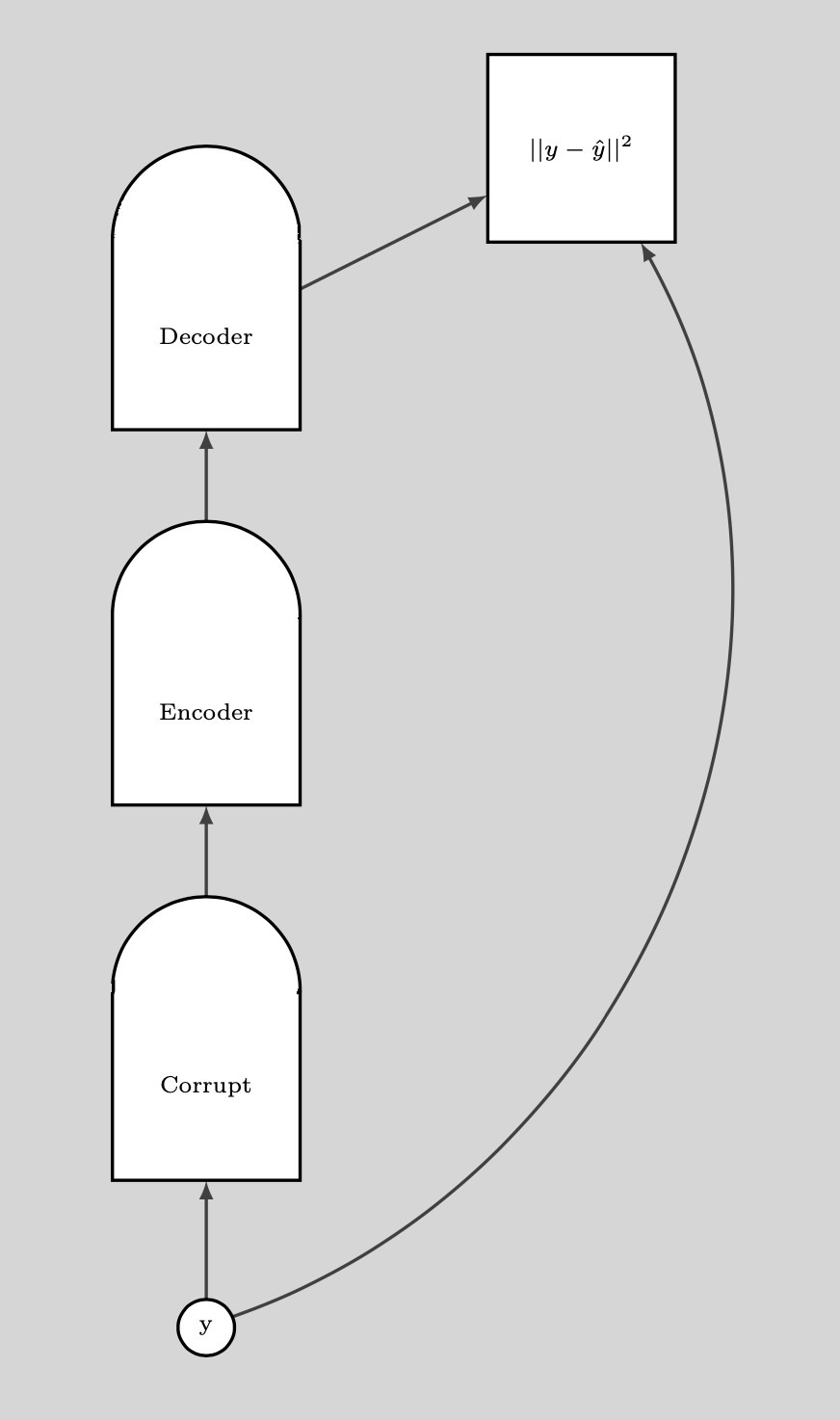
الشكل 8: التدريب

خطوات التدريب:

1. خذ نقطة $ y $ وأفسدها
2. درب المشفر ومفكك التشفير لإعادة بناء نقطة البيانات الأصلية من نقطة البيانات التالفة هذه

إذا تم تدريب DAE بشكل صحيح ، فإن الطاقة تنمو بشكل تربيعي كلما ابتعدنا عن مجمع البيانات.

يوضح المخطط التالي كيف نستخدم DAE.

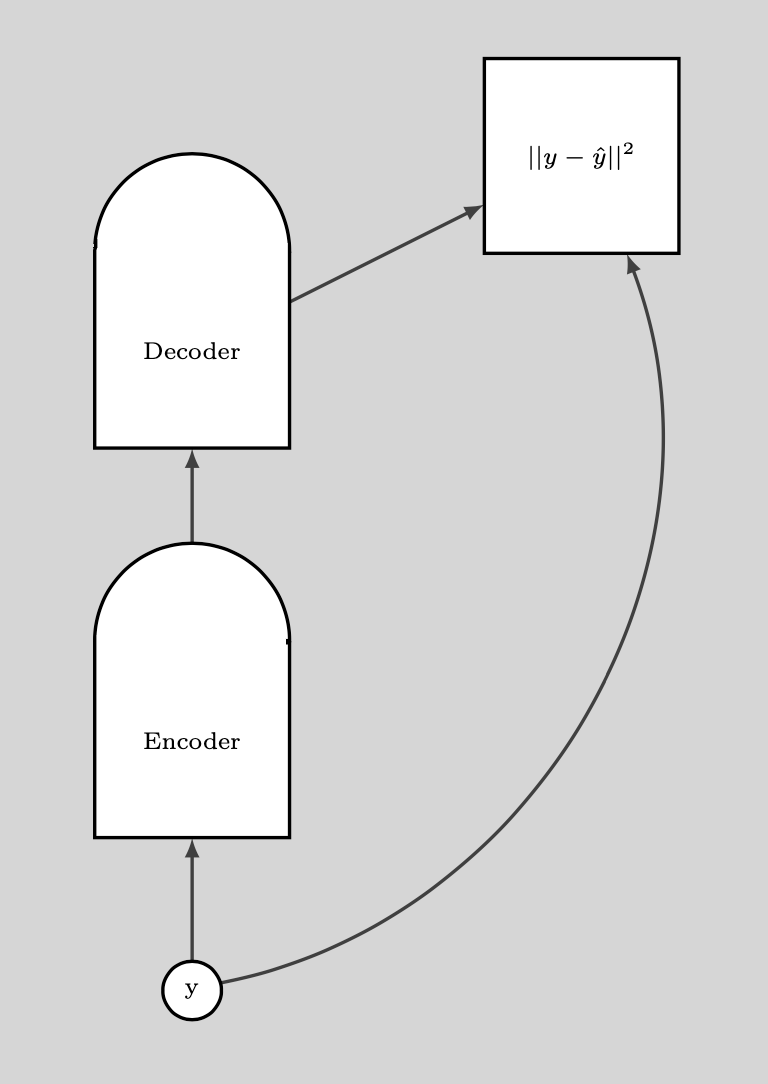
الشكل 9: كيفية استخدام DAE

BERT

يتم تدريب BERT بالمثل ، باستثناء أن الفرغ متقطع لأننا نتعامل مع نص. تتكون تقنية الفساد من إخفاء بعض الكلمات وتتكون خطوة إعادة البناء من محاولة التنبؤ بها. ومن ثم ، يسمى هذا أيضًا المشفر التلقائي المقنع.

الاختلاف التبايني

يقدم لنا الاختلاف التباين طريقة أكثر ذكاءً لإيجاد نقطة $ y $ التي نريد زيادة الطاقة من أجلها. يمكننا إعطاء دفعة عشوائية لنقطة التدريب الخاصة بنا ثم نحرك دالة الطاقة لأسفل باستخدام الانحدار التدريجي. في نهاية المسار ، ندفع الطاقة لأعلى للنقطة التي نهبط عليها. هذا موضح في الرسم أدناه باستخدام الخط الأخضر.

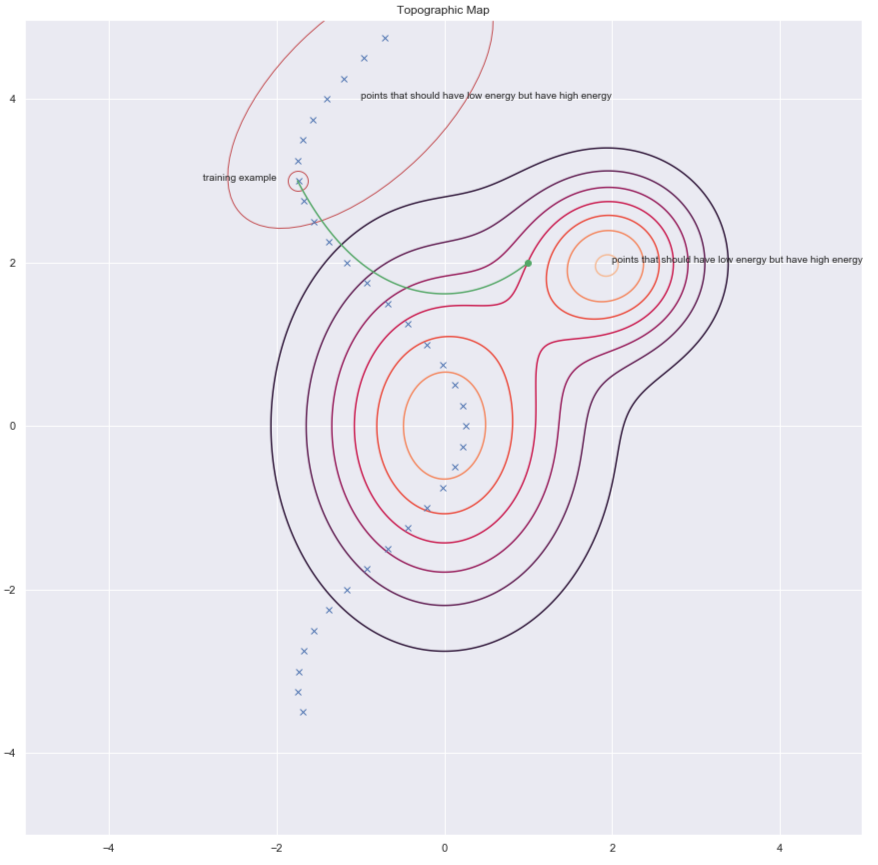
الشكل 10: الاختلاف التبايني