معماريات نماذج الشبكات العصبية التكرارية و الذاكرة قصيرة المدى المطولة

نظرة عامة

الشبكات العصبية التكرارية RNN هي إحدى أنواع المعماريات التي يمكننا استخدامها للتعامل مع تسلسل البيانات. ما هو التسلسل؟ تعلمنا من درس CNN، أن الإشارة يمكن أن تكون إما 1D أو 2D أو 3D حسب المجال. يتم تحديد المجال من خلال ما تقوم بتعيينه وما تقوم بتعيينه إليه. تتعامل معالجة البيانات المتسلسلة بشكل أساسي مع البيانات 1D لأن المجال هو المحور الزمني. ومع ذلك ، يمكنك أيضًا استخدام RNN للتعامل مع البيانات ثنائية الأبعاد ، حيث يكون لديك اتجاهان.

Vanilla مقابل RNN

الشكل 1 عبارة عن رسم تخطيطي لشبكة عصبية فانيليا من ثلاث طبقات. “الفانيليا” مصطلح أمريكي يعني عادي. الفقاعة الوردية هي متجه المدخل x ، و في الوسط توجد الطبقة المخفية باللون الأخضر ، و الطبقة الزرقاء النهائية هي طبقة المُخرج. باستخدام مثال من الإلكترونيات الرقمية على اليمين ، نجد أن هذا يشبه المنطق الاندماجي (combinational logic) ، حيث يعتمد المُخرج الحالي فقط على المدخل الحالي.

الشكل 1: معمارية فانيلا

على النقيض من شبكة الفانيليا العصبية ، في الشبكات العصبية التكرارية ، يعتمد المُخرج الحالي ليس فقط على المدخلات الحالية ولكن أيضًا على حالة النظام ، كما هو موضح في الشكل 2. وهذا يشبه المنطق التسلسلي في الإلكترونيات الرقمية ، حيث أن الناتج يعتمد أيضًا على “flip-flop” (وحدة ذاكرة أساسية في الإلكترونيات الرقمية). لذلك فإن الاختلاف الرئيسي هنا هو أن ناتج شبكة الفانيليا العصبية يعتمد فقط على المدخلات الحالية ، بينما يعتمد في RNN على حالة النظام أيضًا.

الشكل 2: معمارية الشبكات العصبية التكرارية

الشكل 3: معمارية الشبكة العصبية الأساسية

يضيف مخطط يان هذه الأشكال بين الخلايا العصبية لتمثيل التعيين بين موتر وآخر (متجه إلى آخر). على سبيل المثال ، في الشكل 3 ، سيتم تعيين متجه المدخل x عبر هذا العنصر الإضافي إلى التمثيلات المخفية h. هذا العنصر هو في الواقع تحويل تآلفي (affine transformation) ، بمعنى الدوران إضافةً إلى التشويه. ثم من خلال تحويل آخر ، ننتقل من الطبقة المخفية إلى المُخرج النهائي. و بالمثل ، في مخطط RNN ، يمكن أن يكون لديك نفس العناصر الإضافية بين الخلايا العصبية.

الشكل 4: معمارية يان للشبكات العصبية التكرارية

أربعة أنواع من معماريات RNN و أمثلة عليها

الحالة الأولى هي من متجه إلى تسلسل (متجه ← تسلسل). المدخلات هنا عبارة عن فقاعة واحدة و بعد ذلك ستكون هناك تطورات للحالة الداخلية للنظام. مع تطور حالة النظام ، في كل خطوة زمنية سيكون هناك مُخرج واحد محدد.

الشكل 5: من متجه إلى تسلسل

مثال على هذا النوع من المعماريات هو الحصول على المدخلات كصورة واحدة بينما سيكون المخرج عبارة عن سلسلة من الكلمات التي تمثل الأوصاف الإنجليزية لصورة الإدخال. للشرح نستخدم الشكل 6 ، يمكن أن تكون كل خلية زرقاء هنا فهرسًا في قاموس الكلمات الإنجليزية. على سبيل المثال ، إذا كان المُخرج هو جملة “هذه حافلة مدرسية صفراء” (This is a yellow school bus) . تحصل أولاً على فهرس كلمة “This” ثم تحصل على فهرس كلمة “is” وهكذا. يتم عرض بعض نتائج هذه الشبكة أدناه. على سبيل المثال ، في العمود الأول ، يكون الوصف الخاص بالصورة الأخيرة هو “قطيع من الأفيال يمشي عبر حقل عشبي جاف.” ، وهو دقيق للغاية. ثم في العمود الثاني ، تُخرِج الصورة الأولى “كلبان يلعبان في العشب” ، في حين أنه في الواقع ثلاثة كلاب. يوجد في العمود الأخير أمثلة خاطئة مثل “حافلة مدرسية صفراء متوقفة في ساحة انتظار”. بشكل عام ، تظهر هذه النتائج أن هذه الشبكة يمكن أن تفشل بشكل جذري وتعمل بشكل جيد في بعض الأحيان. هذه هي الحالة التي تبدأ من متجه مدخل واحد، و هو تمثيل صورة إلى سلسلة من الرموز ، و التي تمثل أحرف أو كلمات تشكل الجمل الإنجليزية في مثالنا هذا. يسمى هذا النوع من المعماريات بشبكة الانحدار التلقائي. و شبكة الانحدار التلقائي هي شبكة تعطي مخرجات بالنظر إلى أنك تقوم بتغذية المخرج السابق كمدخل.

الشكل 6: متجه إلى تسلسل ، مثال: صورة إلى جملة

النوع الثاني هو التسلسل إلى المتجه النهائي (تسلسل ← متجه نهائي). تحافظ هذه الشبكة على تغذية سلسلة من الرموز وفي النهاية فقط تعطي المخرج النهائي. يمكن أن يكون أحد تطبيقات هذا هو استخدام الشبكة لتفسير بايثون. على سبيل المثال ، المدخلات هي سطور برنامج بايثون.

الشكل 7: تسلسل إلى متجه

الشكل 8: سطور المدخلات في كود بايثون

بعد ذلك ستكون الشبكة قادرة على إخراج الحل الصحيح لهذا البرنامج. برنامج آخر أكثر تعقيدًا مثل هذا:

الشكل 9: سطور مدخلات كود بايثون في حالة أكثر إكتمالا

يجب أن يكون الناتج 12184. يوضح هذان المثالان أنه يمكنك تدريب شبكة عصبية للقيام بهذا النوع من العمليات. نحتاج فقط إلى تغذية سلسلة من الرموز و فرض المخرج النهائي ليكون قيمة محددة.

الثالث هو التسلسل إلى المتجه إلى التسلسل (تسلسل ← متجه ← تسلسل) ، كما هو موضح في الشكل 10. كانت هذه المعمارية هي الطريقة القياسية لأداء ترجمة اللغة. تبدأ بتسلسل الرموز الموضحة هنا باللون الوردي. ثم يتكثف كل شيء في هذا ‘h’ الأخير، والذي يمثل معنى. على سبيل المثال ، يمكن أن يكون لدينا جملة كمدخل ونضغطها مؤقتًا في متجه ، والذي يمثل المعنى أو الرسالة التي نرسلها عبر هذه الجملة. ثم بعد الحصول على هذا المعنى بأي شكل من الأشكال ، تقوم الشبكة بإعادة ترجمته إلى لغة مختلفة. على سبيل المثال ، يمكن ترجمة عبارة “اليوم أنا سعيد جدًا” في سلسلة من الكلمات باللغة الإنجليزية إلى الإيطالية أو الصينية. بشكل عام ، تحصل الشبكة على نوع من الترميز كمدخلات وتحولها إلى معنى مضغوط. أخيرًا ، تقوم وحدة فك التشفير بإعطاء نفس المعنى المضغوط. في الآونة الأخيرة ، رأينا شبكات مثل Transformers ، والتي سنغطيها في الدرس التالي ، تتفوق على هذه الطريقة في مهام ترجمة اللغة. اعتاد هذا النوع من المعماريات أن يكون الأفضل و الأحدث منذ حوالي عامين (2018).

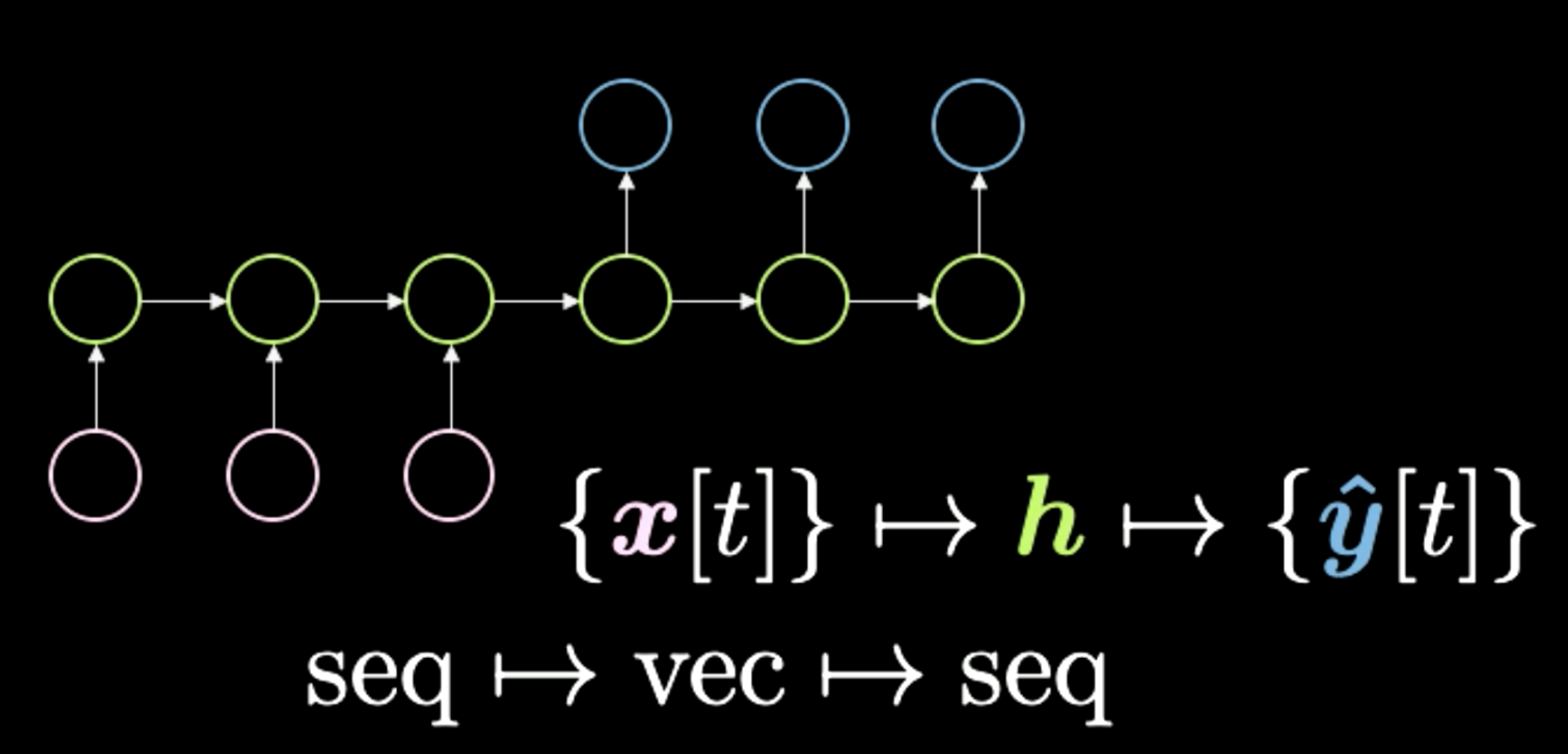
الشكل 10: من تسلسل إلى متجه إلى تسلسل

إذا قمت بإجراء تحليل المكونات الرئيسية (PCA) فوق المساحة الكامنة ، فستحصل على الكلمات مجمعة حسب الدلالات كما هو موضح في هذا الرسم البياني.

الشكل 11: الكلمات مجمعة حسب الدلالات بعد إجراء تحليل المكونات الرئيسية

إذا قمنا بالتكبير ، فسنرى أنه في نفس الموقع هناك كل الأشهر ، مثل يناير ونوفمبر.

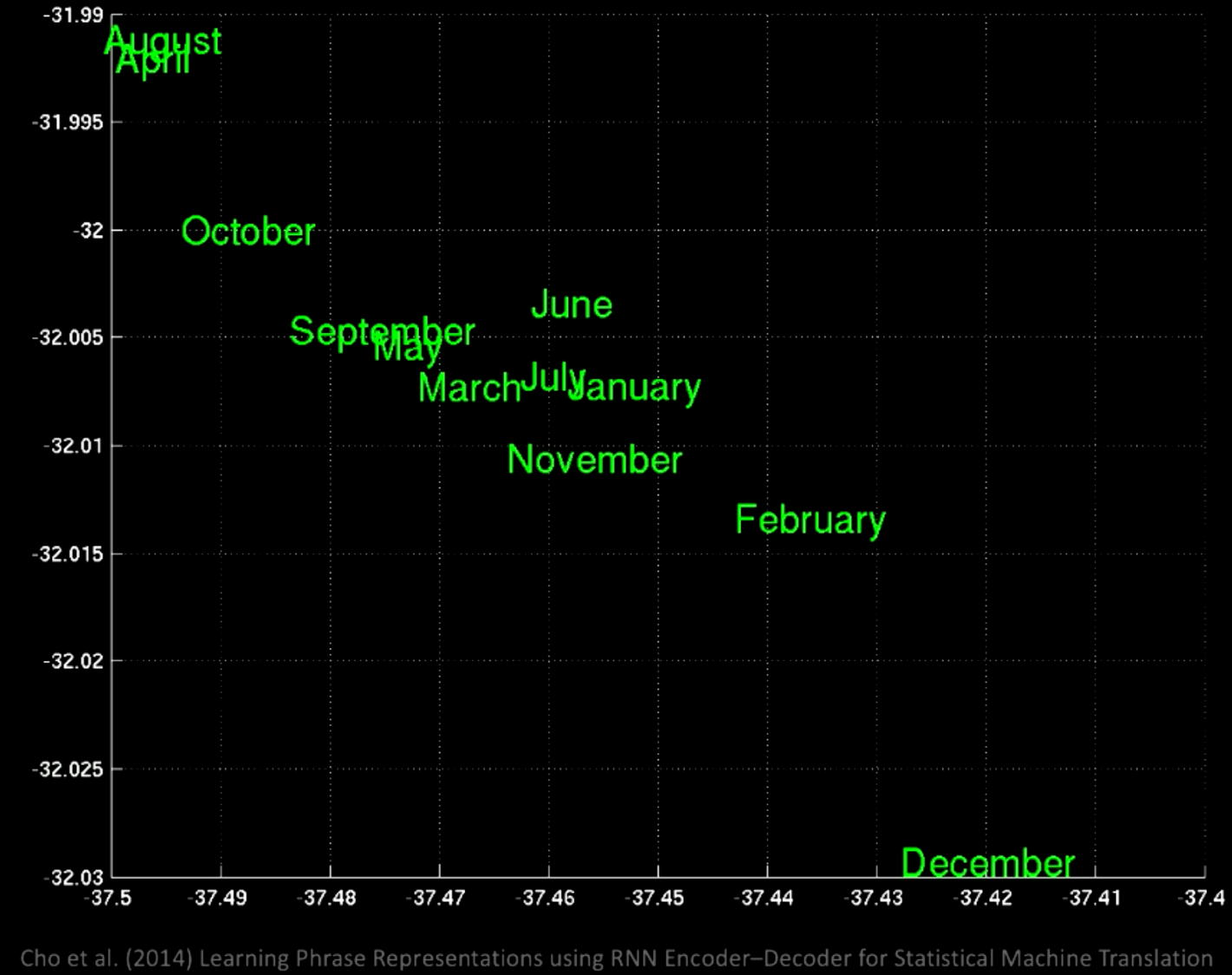
الشكل 12: تكبير مجموعات الكلمات

إذا ركزت على منطقة مختلفة ، فستحصل على عبارات مثل “قبل أيام قليلة” “الأشهر القليلة المقبلة” إلخ.

الشكل 13: مجموعات الكلمات في منطقة أخرى

من هذه الأمثلة ، نرى أن المواقع المختلفة سيكون لها بعض المعاني المشتركة المحددة.

يوضح الشكل 14 كيف أن تدريب هذا النوع من الشبكات سوف يلتقط بعض الميزات. على سبيل المثال في هذه الحالة ، يمكنك أن ترى أن هناك متجهًا يربط بين الرجل و المرأة وآخر بين الملك و الملكة ، مما يعني أن المرأة ناقص الرجل ستكون مساوية للملكة ناقص الملك. ستحصل على نفس المسافة المطبقة على حالات مثل الذكور والإناث. مثال آخر هو يمشي للمشي ويسبح للسباحة. يمكنك دائمًا تطبيق هذا النوع من التحويل الخطي المحدد بالانتقال من كلمة إلى أخرى أو من بلد إلى عاصمة.

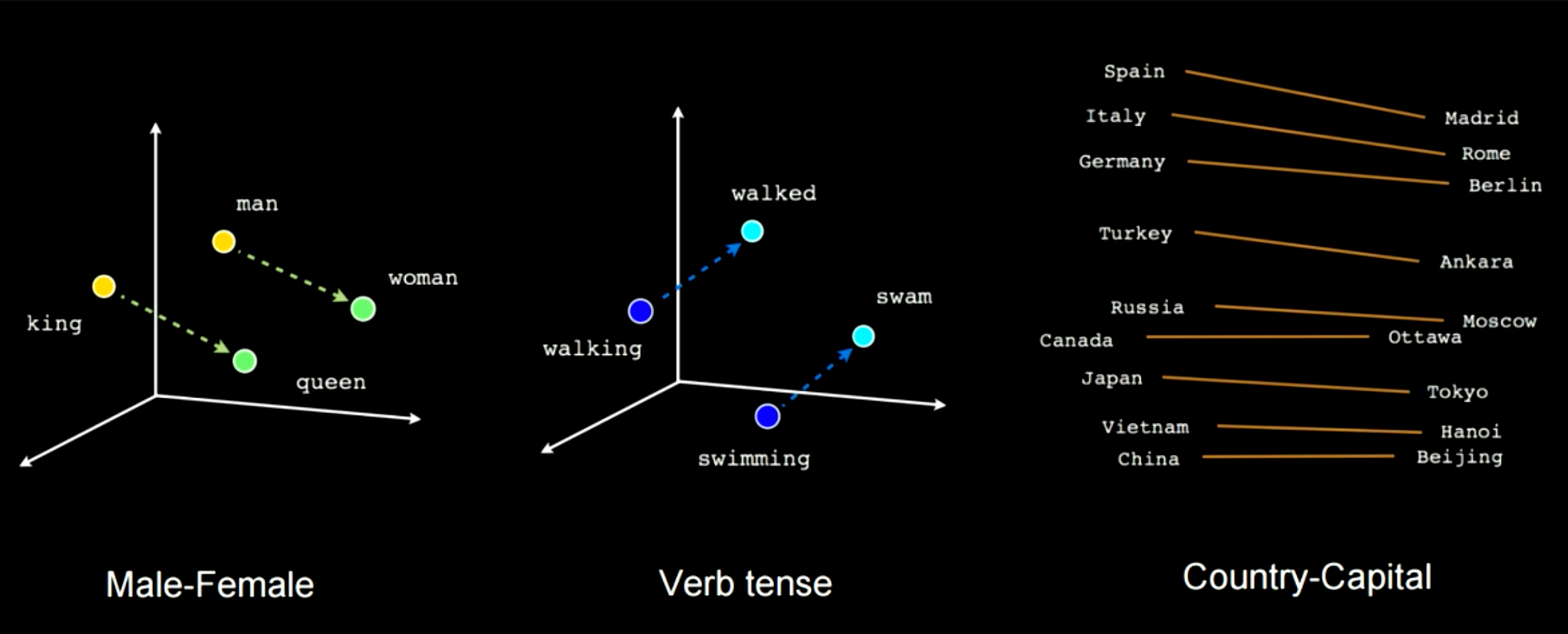
الشكل 14: ميزات الخصائص المختارة أثناء التدريب

الحالة الرابعة والأخيرة هي التسلسل إلى التسلسل (تسلسل ← تسلسل). في هذه الشبكة ، عندما تبدأ في تغذية المدخلات ، تبدأ الشبكة في توليد المخرجات. مثال على هذا النوع من المعماريات هو T9 ، إذا كنت تتذكر استخدام هاتف Nokia ، فإنك كنت تحصل على اقتراحات نصية أثناء الكتابة. مثال آخر هو تحويل الحديث إلى تسميات توضيحية. أحد الأمثلة الرائعة هو ال RNN الكاتب هذا. عندما تبدأ في كتابة “حلقات زحل تتلألأ أثناء” ، فإنه يقترح عليك “نظر الرجلان إلى بعضهما البعض”. لقد تم تدريب هذه الشبكة على بعض روايات الخيال العلمي بحيث يمكنك فقط كتابة شيء ما والسماح لها بتقديم اقتراحات لمساعدتك في كتابة كتاب. يظهر مثال آخر في الشكل 16. قم بإدخال الموجه العلوي ثم ستحاول هذه الشبكة إكمال الباقي.

الشكل 15: تسلسل إلى تسلسل

الشكل 16: مثال عن الإكمال التلقائي للنص عبر نموذج من التسلسل إلى التسلسل

الانتشار العكسي عبر الزمن

معمارية النموذج

من أجل تدريب RNN ، يجب استخدام الانتشار العكسي عبر الزمن (BPTT). يتم إعطاء معمارية نموذج RNN في الشكل أدناه. يستخدم التصميم الأيسر تمثيل الحلقات بينما الشكل الأيمن يفتح الحلقة في صف واحد بمرور الوقت.

الشكل 17: الانتشار العكسي عبر الزمن

يتم ذكر التمثيلات المخفية كـ \(\begin{aligned} \begin{cases} h[t]&= g(W_{h}\begin{bmatrix} x[t] \\ h[t-1] \end{bmatrix} +b_h) \\ h[0]&\dot=\ \boldsymbol{0},\ W_h\dot=\left[ W_{hx} W_{hh}\right] \\ \hat{y}[t]&= g(W_yh[t]+b_y) \end{cases} \end{aligned}\)

تشير المعادلة الأولى إلى دالة لاخطية مطبقة على تدوير نسخة من المدخلات المكدسة حيث يتم إلحاق الترتيب السابق للطبقة المخفية. في البداية ، يتم تعيين $h[0]$ ك 0. لتبسيط المعادلة ، يمكن كتابة $W_h$ كمصفوفتين منفصلتين، $\left[ W_{hx}\ W_{hh}\right]$ ، وبالتالي يمكن أحيانًا ذكر التحويل على أنه: \(W_{hx}\cdot x[t]+W_{hh}\cdot h[t-1]\)

والذي يتوافق مع تمثيل المكدس للمدخلات.

يتم حساب $y[t]$ في الدورة الأخيرة و من ثم يمكننا استخدام قاعدة السلسلة (chain rule) لعكس انتشار الخطأ إلى الخطوة الزمنية السابقة.

معالجة-الحزم في نمذجة اللغات

عند التعامل مع سلسلة من الرموز ، يمكننا تقسيم النص إلى أحجام مختلفة. على سبيل المثال ، عند التعامل مع التسلسلات الموضحة في الشكل التالي ، يمكن تطبيق معالجة-الحزم أولاً ، حيث يتم الاحتفاظ بالمجال الزمني عمودياً. في هذه الحالة ، يتم تعيين حجم الحزمة على 4.

الشكل 18: معالجة-الحزم

إذا تم ضبط فترة T في BPTT على 3 ، يتم تحديد المدخل الأول $x[1:T]$ و المخرج $y[1:T]$ لـ RNN على أنه \(\begin{aligned} x[1:T] &= \begin{bmatrix} a & g & m & s \\ b & h & n & t \\ c & i & o & u \\ \end{bmatrix} \\ y[1:T] &= \begin{bmatrix} b & h & n & t \\ c & i & o & u \\ d & j & p & v \end{bmatrix} \end{aligned}\)

عند إجراء RNN على الحزمة الأولى ، أولاً ، نقوم بتغذية $x[1] = [a\ g\ m\ s]$ في RNN ونفرض المخرج ليكون $y[1] = [b\ h\ n\ t]$. سيتم إرسال التمثيل المخفي $h[1]$ للأمام إلى الخطوة التالية لمساعدة RNN على توقع $y[2]$ من خلال $x[2]$ بعد إرسال $h[T-1]$ إلى المجموعة الأخيرة من $x[T]$ و $y[T]$ ، قمنا بقص عملية الانتشار المتدرج لكل من $h[T]$ و $h[0]$ بحيث لا تنتشر التدرجات إلى اللانهائية (فصل في Pytorch ). العملية برمتها موضحة في الشكل أدناه.

الشكل 19: معالجة-الحزم

تلاشي و انفجار التدرجات

المشكلة

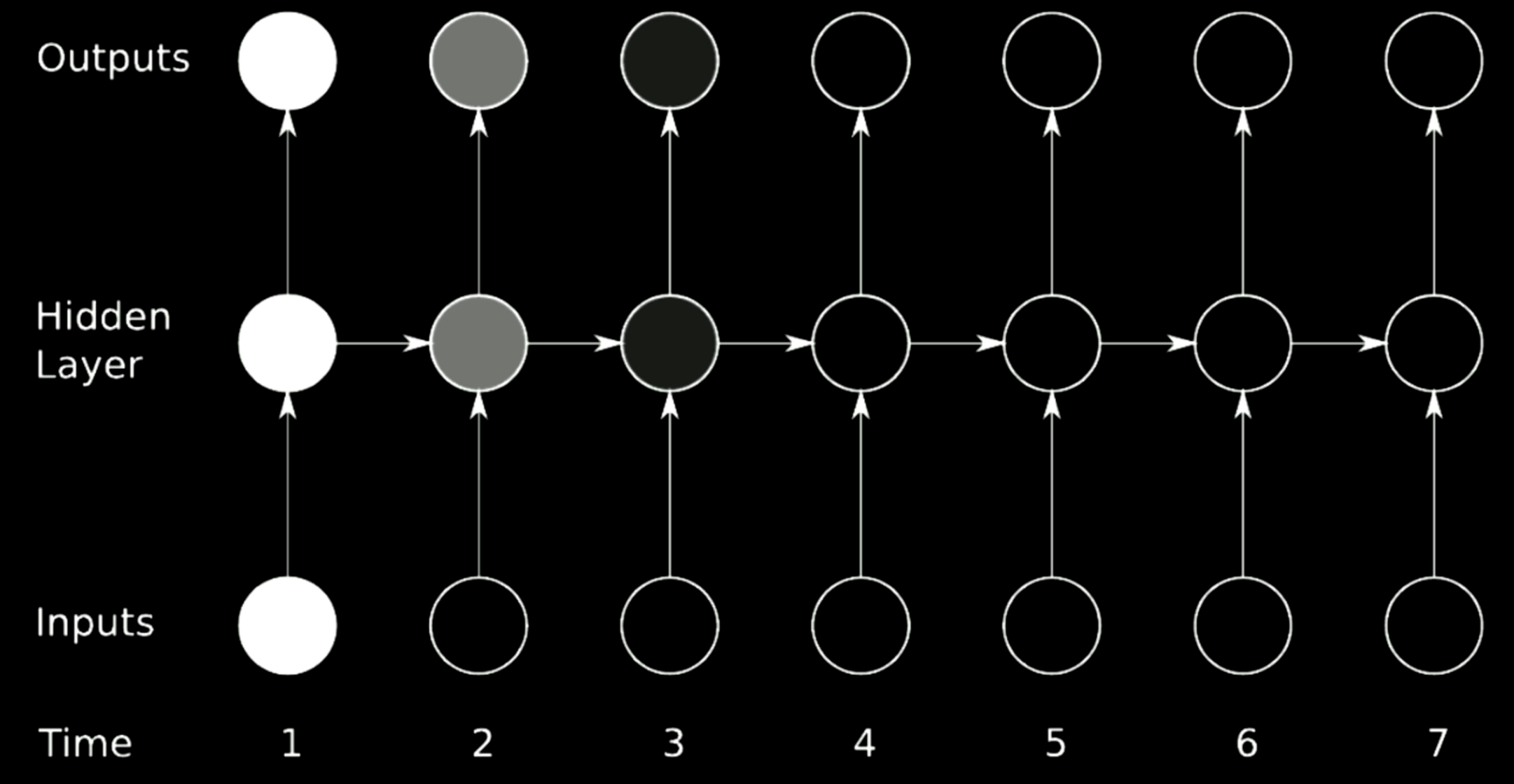
الشكل 20: مشكلة التلاشي

الشكل أعلاه هو معمارية RNN نموذجية. من أجل إجراء تناوب على الخطوات السابقة في RNN ، نستخدم المصفوفات ، والتي يمكن اعتبارها أسهم أفقية في النموذج أعلاه. نظرًا لأن المصفوفات يمكنها تغيير حجم المخرجات ، إذا كان المحدد الذي نختاره أكبر من 1 ، فسوف يتضخم التدرج بمرور الوقت و يسبب انفجار للتدرج. بشكل نسبي ، إذا كانت قيم ذاتية (eigenvalue) التي نختارها صغيرة خلال 0، فإن عملية الانتشار ستقلص التدرجات وتؤدي إلى تلاشي التدرج.

في RNNs نموذجية ، سيتم نشر التدرجات من خلال جميع الأسهم الممكنة ، مما يوفر للتدرجات فرصة كبيرة للاختفاء أو الانفجار. على سبيل المثال ، يكون التدرج اللوني في الوقت 1 كبيرًا ، والذي يُشار إليه باللون الساطع. عندما يمر خلال دورة واحدة ، يتقلص التدرج كثيرًا وفي الوقت 3 ،يكون قد تم قتله.

الحل

الطريقة المثالية لمنع التدرجات من الانفجار أو التلاشي هي تخطي الوصلات. لتحقيق ذلك ، يمكن استخدام شبكات الضرب.

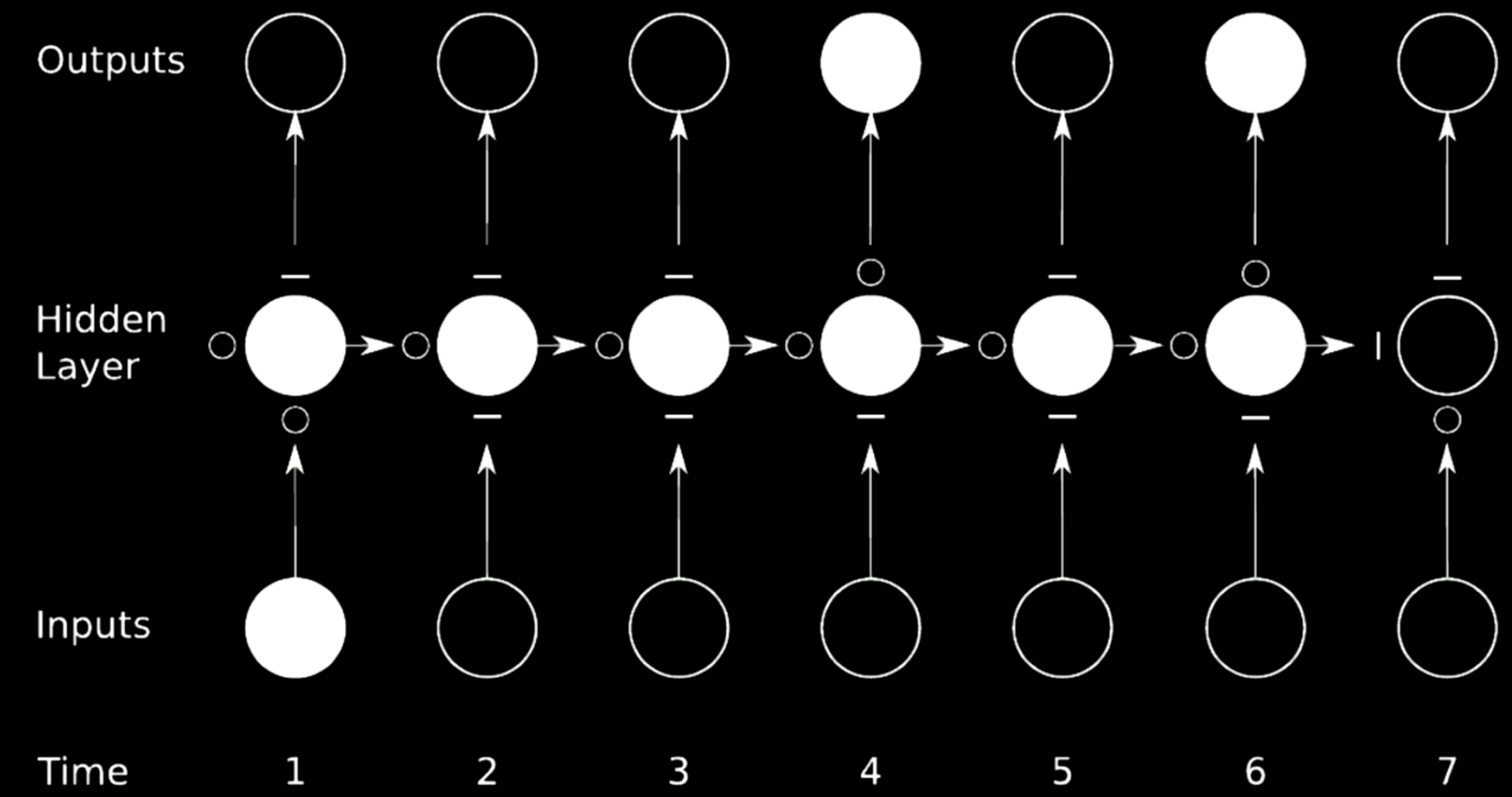
الشكل 21: تخطي الاتصال

في الحالة المذكورة أعلاه ، قمنا بتقسيم الشبكة الأصلية إلى 4 شبكات. خذ الشبكة الأولى على سبيل المثال. تأخذ قيمة من المدخل في الوقت 1 و يرسل المخرج إلى الحالة الوسطية الأولى في الطبقة المخفية. تحتوي الحالة على 3 شبكات أخرى حيث تسمح “∘” للتدرجات بالمرور أثناء إعاقة “−” للانتشار. تسمى هذه التقنية بالشبكة المتكررة ذات البوابات.

LSTM هو واحد من الRNN المنتشرة و سيتم تقديمه بالتفصيل في الأقسام التالية.

الذاكرة قصيرة المدى المطولة

معمارية النموذج

فيما يلي المعادلات التي تعبر عن نموذج LSTM. يتم تمييز بوابة المدخلات بواسطة المربعات الصفراء ، والتي ستكون عبارة عن تحويل تآلفي. سوف يتضاعف تحويل هذا المدخل في $c[t]$ ، وهي البوابة المرشحة لدينا.

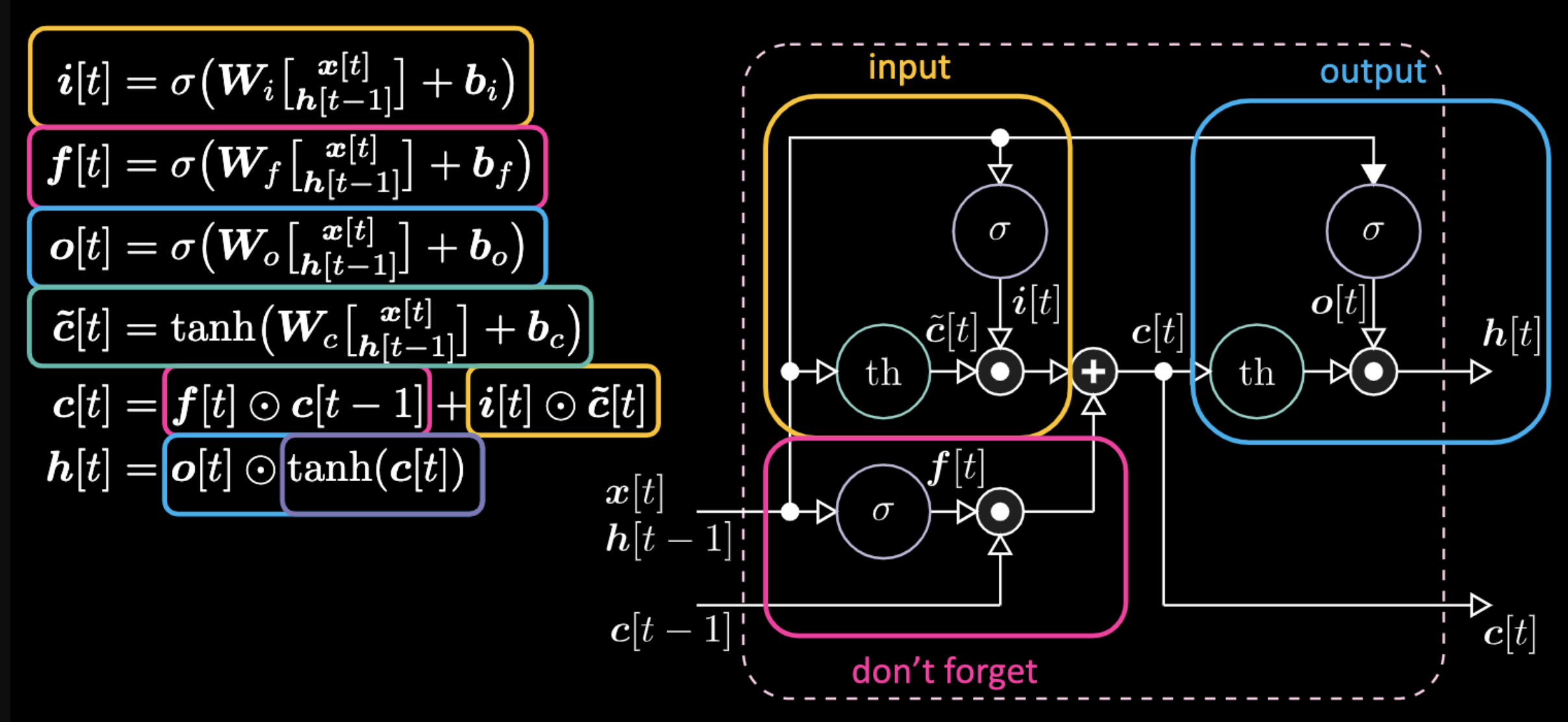
الشكل 22: معمارية نموذج الذاكرة قصيرة المدى المطولة

لا تنس أن البوابة تُضاعف القيمة السابقة لذاكرة الخلية $c[t-1]$. و أيضا إجمالي قيمة الخلية $c[t]$ هو بوابة الذاكرة بالإضافة إلى بوابة المدخل. التمثيل النهائي المخفي هو الضرب على أساس العنصر بين بوابة المخرج $o[t]$ و نسخة الظل الزائدي للخلية $c[t]$. أخيرًا، بوابة المرشح $\tilde{c}[t]$ هي ببساطة شبكة متكررة. لذلك لدينا $o[t]$ لتعديل المخرج، و $f[t]$ لتعديل بوابة الذاكرة ، و $i[t]$ لتعديل بوابة المدخل. كل هذه التفاعلات بين الذاكرة والبوابات هي تفاعلات مضاعفة. $i[t]$ و $f[t]$ و $o[t]$ كلها عبارة عن سيجمويد، محصورة بين صفر و واحد. و من ثم فعند الضرب في الصفر يكون لديك بوابة مغلقة، و عند الضرب في واحد يكون لديك بوابة مفتوحة.

كيف نقوم بإيقاف تشغيل المخرج؟ لنفترض أن لدينا تمثيل داخلي أرجواني $th$ و صفر في بوابة المخرج. إذا سيكون الناتج صفرًا مضروبًا في شيء ما ، ونحصل على صفر. إذا وضعنا واحدًا في بوابة المخرج، فسنحصل على نفس قيمة التمثيل الأرجواني.

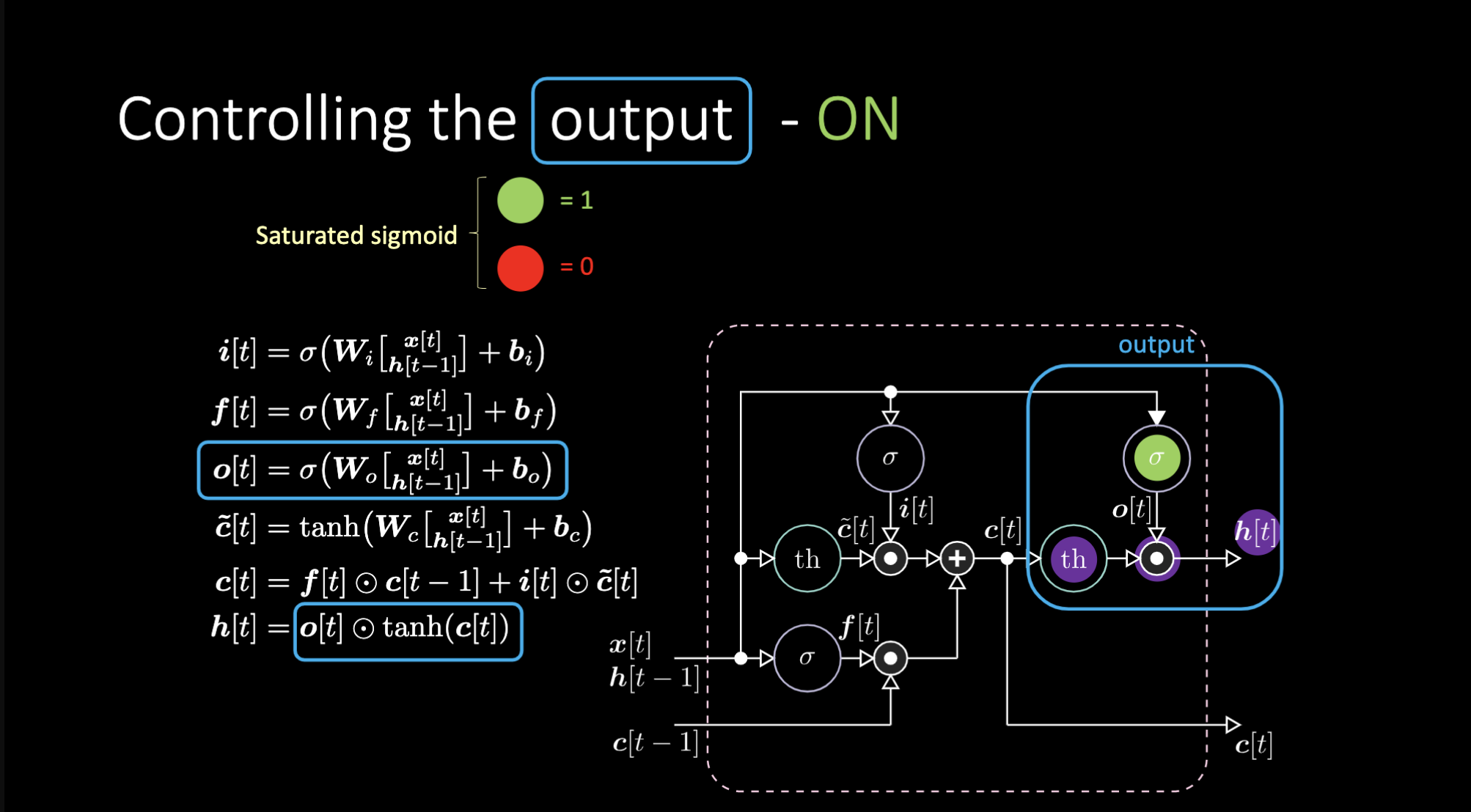
الشكل 23: معمارية "الذاكرة قصيرة المدى المطولة" - تشغيل المخرج

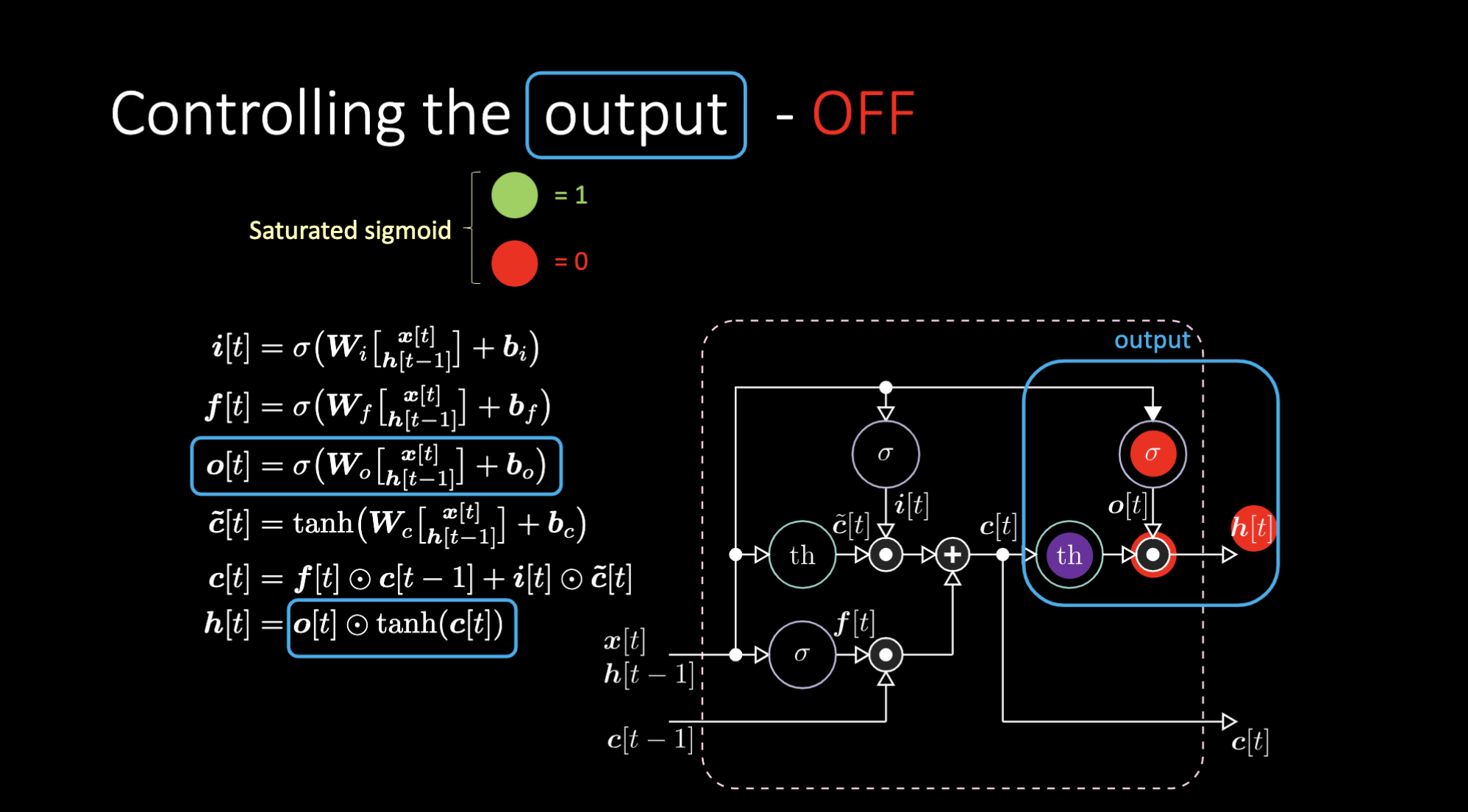
الشكل 24: معمارية "الذاكرة قصيرة المدى المطولة" - تعطيل المخرج

وبالمثل ، يمكننا التحكم في الذاكرة. على سبيل المثال ، يمكننا إعادة تعيينها من خلال جعل $f[t]$ و $i[t]$ أصفار. بعد الضرب و الجمع، يكون لدينا صفر داخل الذاكرة. خلاف ذلك، يمكننا الاحتفاظ بالذاكرة، من خلال الاستمرار في استبعاد التمثيل الداخلي $th$ مع الاحتفاظ بواحد في $f[t]$. و من ثم، فإن المجموع يحصل على $c[t-1]$ ويستمر في إرساله. أخيرًا ، يمكننا أن نكتب بحيث يمكننا الحصول على واحد في بوابة المدخل، يصبح الضرب أرجوانيًا ، ثم نضبط صفرًا في بوابة الذاكرة (يمكننا أيضا أن نسميها بوابة “لا تنسى”) حتى تنسى بالفعل.

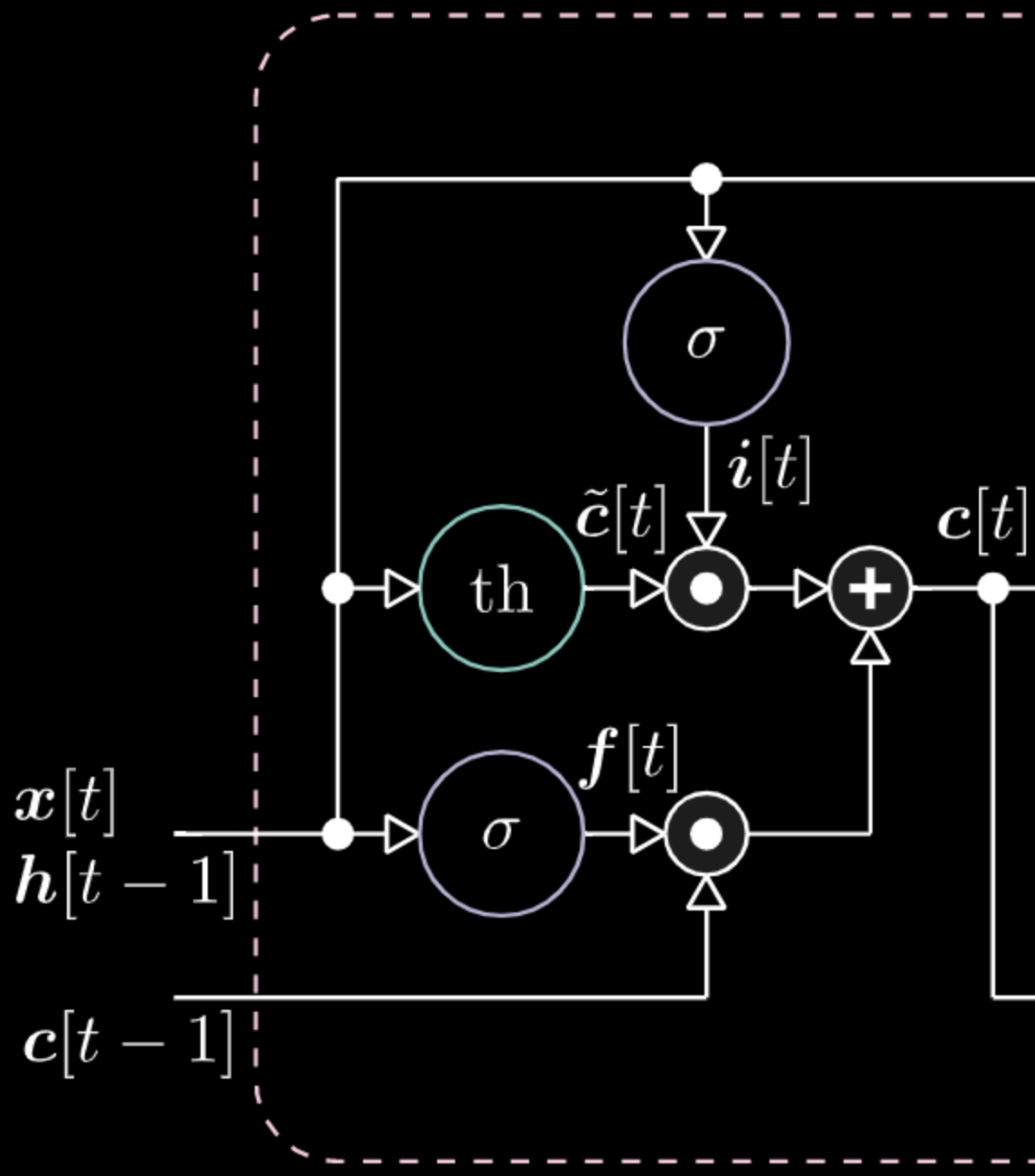
الشكل 25: التجسيد المرئي لخلية الذاكرة

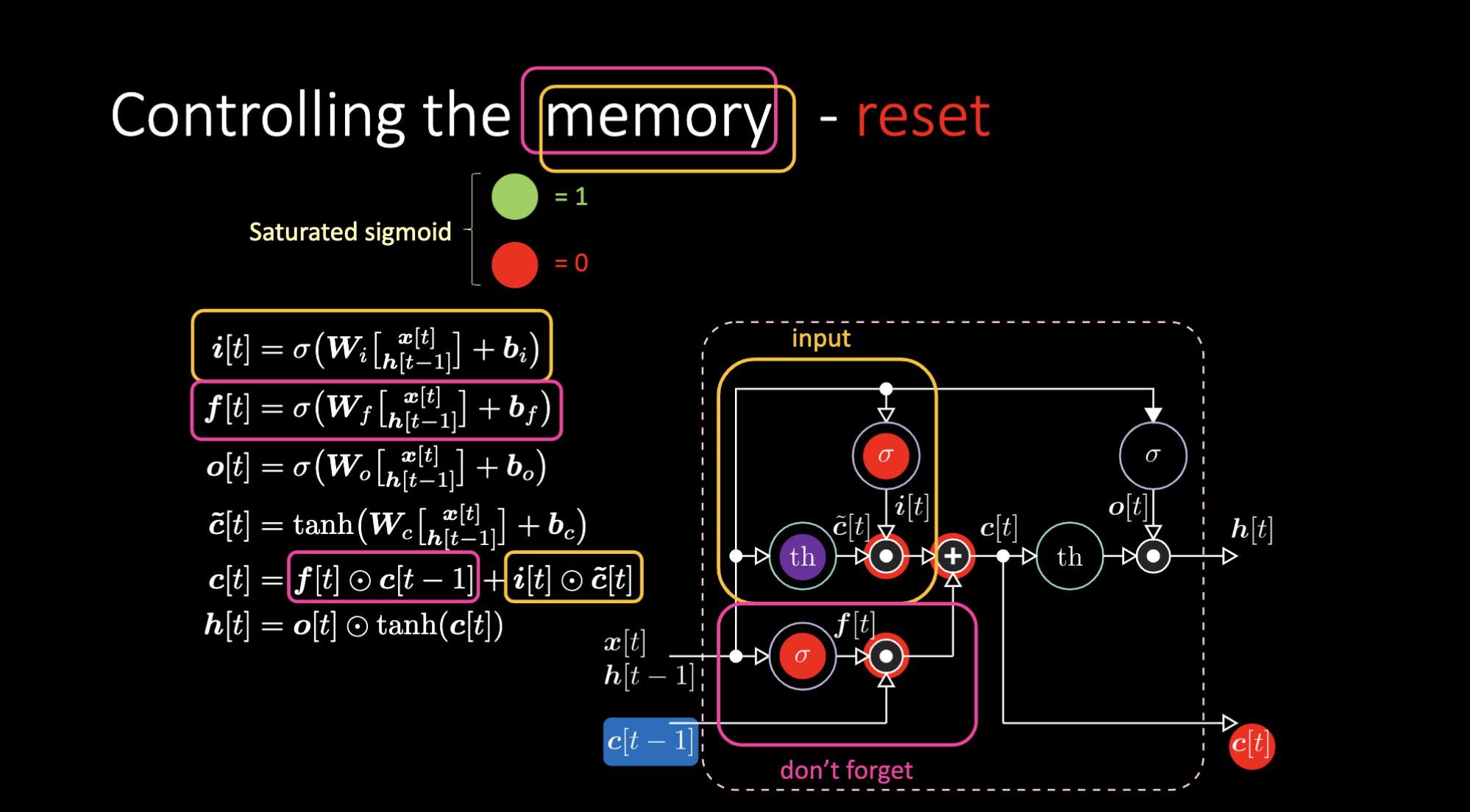
الشكل 26: معمارية "الذاكرة قصيرة المدى المطولة" - إعادة الذاكرة

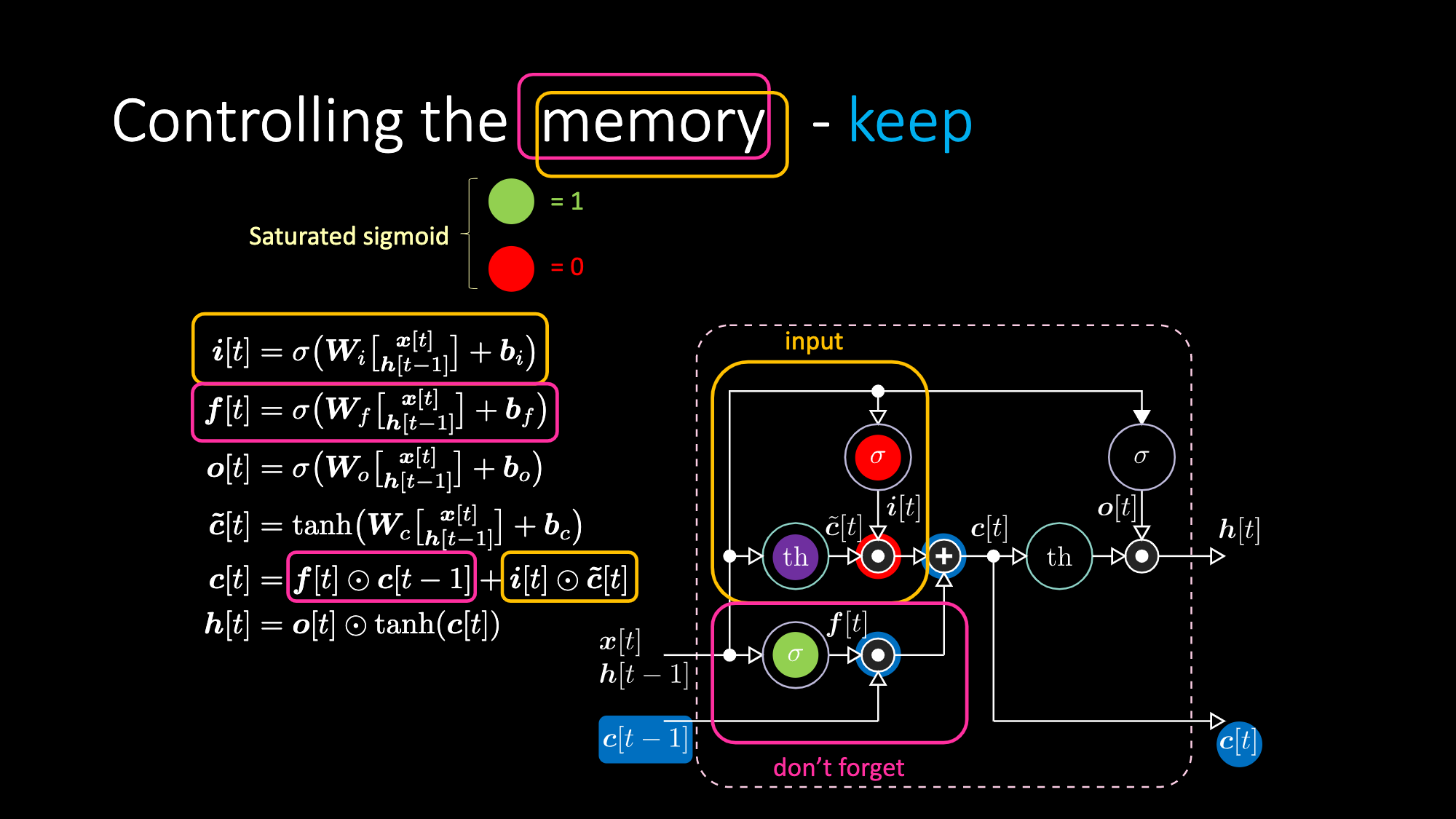
الشكل 27: معمارية "الذاكرة قصيرة المدى المطولة" - الحفاظ على الذاكرة

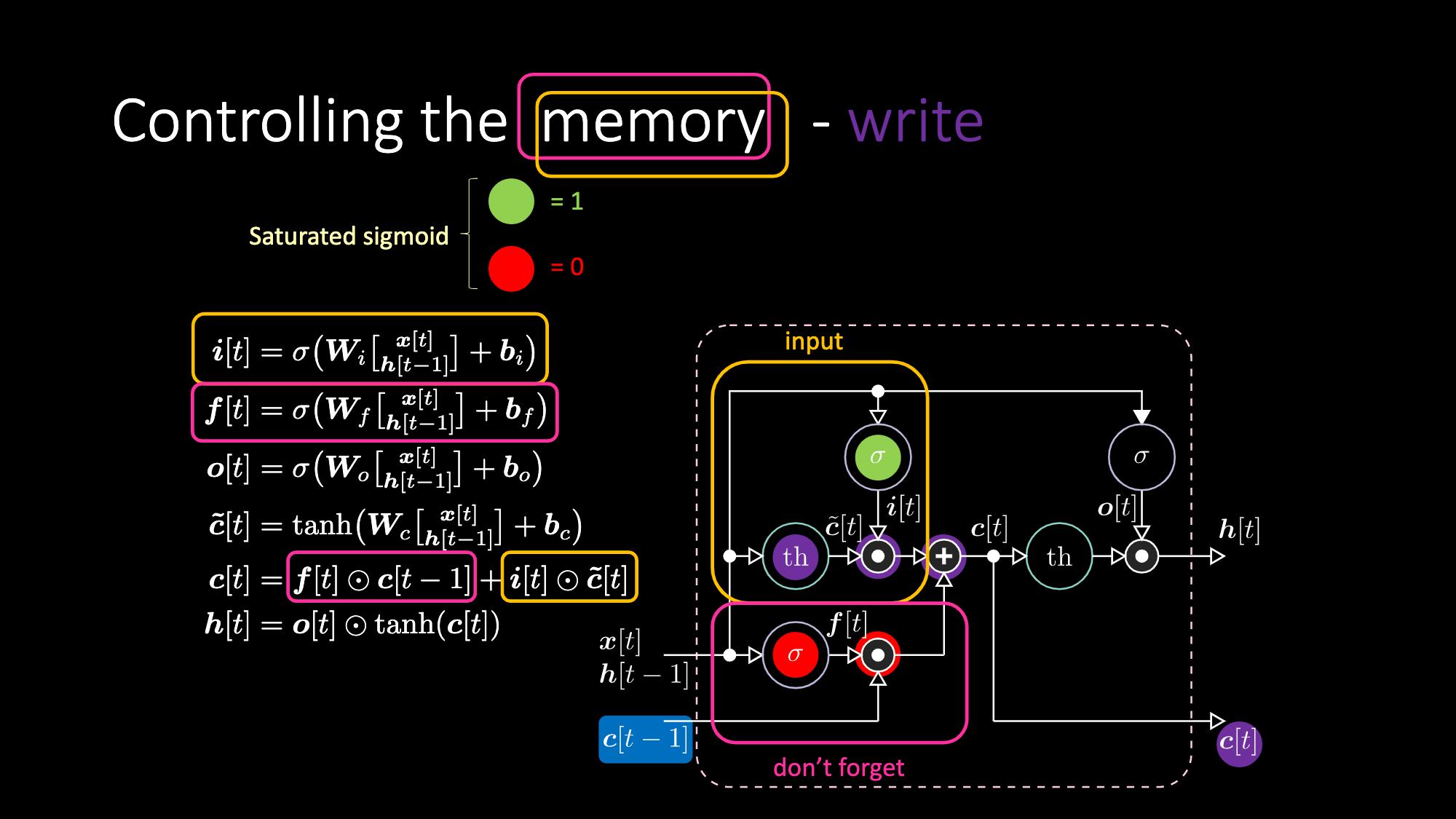
الشكل 28: معمارية "الذاكرة قصيرة المدى المطولة" - كتابة الذاكرة

دفتر الأمثلة

تصنيف التسلسل

الهدف هو تصنيف تسلسلات. يتم تمثيل العناصر والأهداف محليًا (متجهات المدخل مع بت (bit) واحد غير صفري). يبدأ التسلسل بـ B ، وينتهي بـ E (“رمز التشغيل”) ، و يتكون بخلاف ذلك من الرموز المختارة عشوائيًا من المجموعة {a, b, c, d} باستثناء عنصرين في الموضعين $t_1$ و $t_2$ وهما إما X أو Y. بالنسبة لمستوى الصعوبة (DifficultyLevel.HARD)، يتم اختيار طول التسلسل عشوائيًا بين 100 و 110 ، ويتم اختيار $t_1$ عشوائيًا بين 10 و 20 ، ويتم اختيار $t_2$ عشوائيًا بين 50 و 60. هناك 4 فئات تسلسلية Q، R، S و U اللتان تعتمدان على الترتيب الزمني لـX و Y. القواعد هي: X, X -> Q; X, Y -> R; Y, X -> S; Y, Y -> U.

1). استكشاف مجموعة البيانات

نوع الإرجاع من مولد البيانات هو صف بطول 2. العنصر الأول في الصف هو حزمة التسلسلات ذات الشكل $(32, 9, 8)$. هذه هي البيانات التي سيتم تغذيتها في الشبكة. هناك ثمانية رموز مختلفة في كل صف (X, Y, a, b, c, d, B, E). كل صف عبارة عن متجه واحد. يمثل تسلسل الصفوف سلسلة من الرموز. تم حشو الصف الأول الصفري. نستخدم الحشو (padding) عندما يكون طول التسلسل أقصر من الحد الأقصى لطول الحزمة . العنصر الثاني في الصف هو الحزمة المقابلة من معلمات الفئات ذات الشكل $(32, 4)$ ، نظرًا لأن لدينا 4 فئات (Qو Rو Sو U). التسلسل الأول هو: BbXcXcbE. تم تسمية الفئة التي تم فك ترميزها ب $[1, 0, 0, 0]$ ، المقابلة لـ Q.

الشكل 29: مثال على متجه المدخل

2). تحديد النموذج و تدريبه

دعونا ننشئ شبكة تكرارية بسيطة بالإضافة إلى LSTM ، وندربهم لمدة 10 “فترات”. تذكر! في حلقة ‘التدريب’ يجب أن نركز دائمًا على خمس خطوات :

• أن يكون النموذج في تقدم
• حساب الخسارة
• أن تكون التدرجات المؤقتة صفر
• أن ننجز الإنتشار العكسي لحساب المشتق الجزئي لدالة الخسارة فيما يتعلق بالمعلمات
• التدخل في الاتجاه المعاكس للتدرج

الشكل 30: شبكة تكرارية بسيطة *مقابل* ذاكرة قصيرة المدى مطولة - 10 فترات

مع مستوى صعوبة سهل نوعا ما، تحصل RNN على دقة 50٪ بينما تحصل LSTM على 100٪ بعد 10 ‘فترات’. لكن LSTM لديها أربعة أضعاف أوزان RNN ولها طبقتان مخفيتان ، لذا فهي ليست مقارنة عادلة. بعد 100 ‘فترة’، تحصل RNN أيضًا على دقة 100٪ ، و تستغرق وقتًا أطول من LSTM للتدريب.

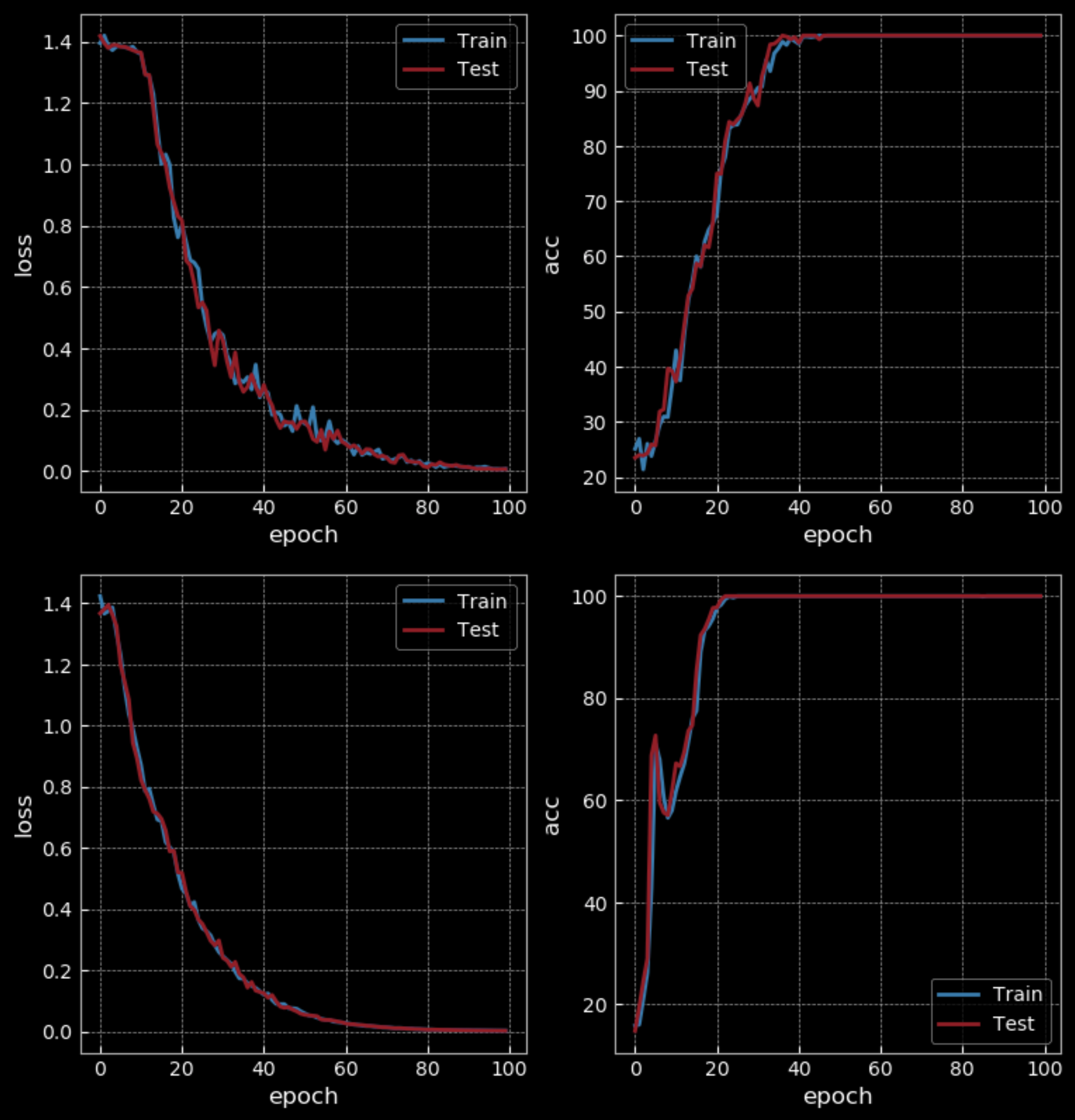
الشكل 31: شبكة تكرارية بسيطة *مقابل* ذاكرة قصيرة المدى مطولة - 100 فترة

إذا قمنا بزيادة صعوبة جزء التدريب (باستخدام تسلسلات أطول) ، فسنرى فشل RNN بينما يستمر LSTM في العمل.

الشكل 32: التجسيد المرئي لقيمة الحالة المخفية

التجسيد المرئي أعلاه يرسم قيمة الحالة المخفية بمرور الوقت في LSTM. سنرسل المدخلات من خلال الظل الزائدي، بحيث إذا كان الإدخال أقل من $-2.5$ ، فسيتم تعيينه إلى $-1$ ، وإذا كان أعلى من $2.5$ ، فسيتم تعيينه إلى $1$. لذلك في هذه الحالة ، يمكننا أن نرى اختيار الطبقة المخفية المحددة على X (الصف الخامس في الصورة) ثم أصبحت حمراء حتى حصلنا على X الأخرى. لذلك ، يتم تشغيل الوحدة المخفية الخامسة للخلية من خلال مراقبة X وتهدأ بعد رؤية X الأخرى. هذا يسمح لنا بالتعرف على فئة التسلسل.

صدى الإشارة

يعد صدى خطوات الإشارة n مثالًا على مهمة متزامنة(متعدد - متعدد) . على سبيل المثال ، تسلسل المدخل الأول هو "1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 ..." ، و تسلسل الهدف الأول هو "0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 ...". في هذه الحالة ، يكون المخرج بعد ثلاث خطوات. لذلك نحن بحاجة إلى ذاكرة عمل قصيرة الوقت للحفاظ على المعلومات. بينما في نموذج اللغة ، يقول شيئًا لم يُقال من قبل.

قبل أن نرسل التسلسل الكامل إلى الشبكة ونجبر الهدف النهائي على أن يكون شيئًا ما ، نحتاج إلى قطع التسلسل الطويل إلى أجزاء صغيرة. أثناء تغذية قطعة جديدة ، نحتاج إلى تتبع الحالة المخفية وإرسالها كمدخلات للحالة الداخلية عند إضافة الجزء الجديد التالي. في LSTM ، يمكنك الاحتفاظ بالذاكرة لفترة طويلة طالما لديك سعة كافية. في RNN ، بعد أن تصل إلى طول معين ، تبدأ في نسيان ما حدث في الماضي.