الشبكات العصبية التكرارية، وحدات البوابات المتكررة، الذاكرة القصيرة المدى المطولة، الانتباه، تسلسل/تسلسل و شبكة الذاكرة.

معماريات التعلم العميق

في التعلم العميق، هناك نماذج مختلفة لأداء مهام مختلفة. تتضمن خبرة التعلم العميق تصميم المعماريات (الخوارزميات) لإنجاز مهام معينة. على غرار كتابة برامج باستخدام الخوارزميات لإعطاء تعليمات محددة لجهاز الكمبيوتر كما في الأيام الخوالي، يقلل التعلم العميق من مهمة معقدة إلى رسم بياني للوحدات الوظيفية (ربما الديناميكية)، والتي يتم الانتهاء من مهامها عن طريق التعلم.

كما هو الحال مع ما رأيناه مع الشبكات الإلتفافية، فإن معمارية الشبكة مهمة جدا.

الشبكات العصبية التكرارية

في الشبكة العصبية الإلتفافية، لا يمكن أن يحتوي الرسم البياني أو الروابط ما بين النماذج على حلقات (loops). يوجد على الأقل ترتيب جزئي بين النماذج بحيث تكون المدخلات متاحة عندما نحسب المخرجات.

كما هو مبين في الشكل 1، توجد حلقات في الشبكات العصبية التكرارية.

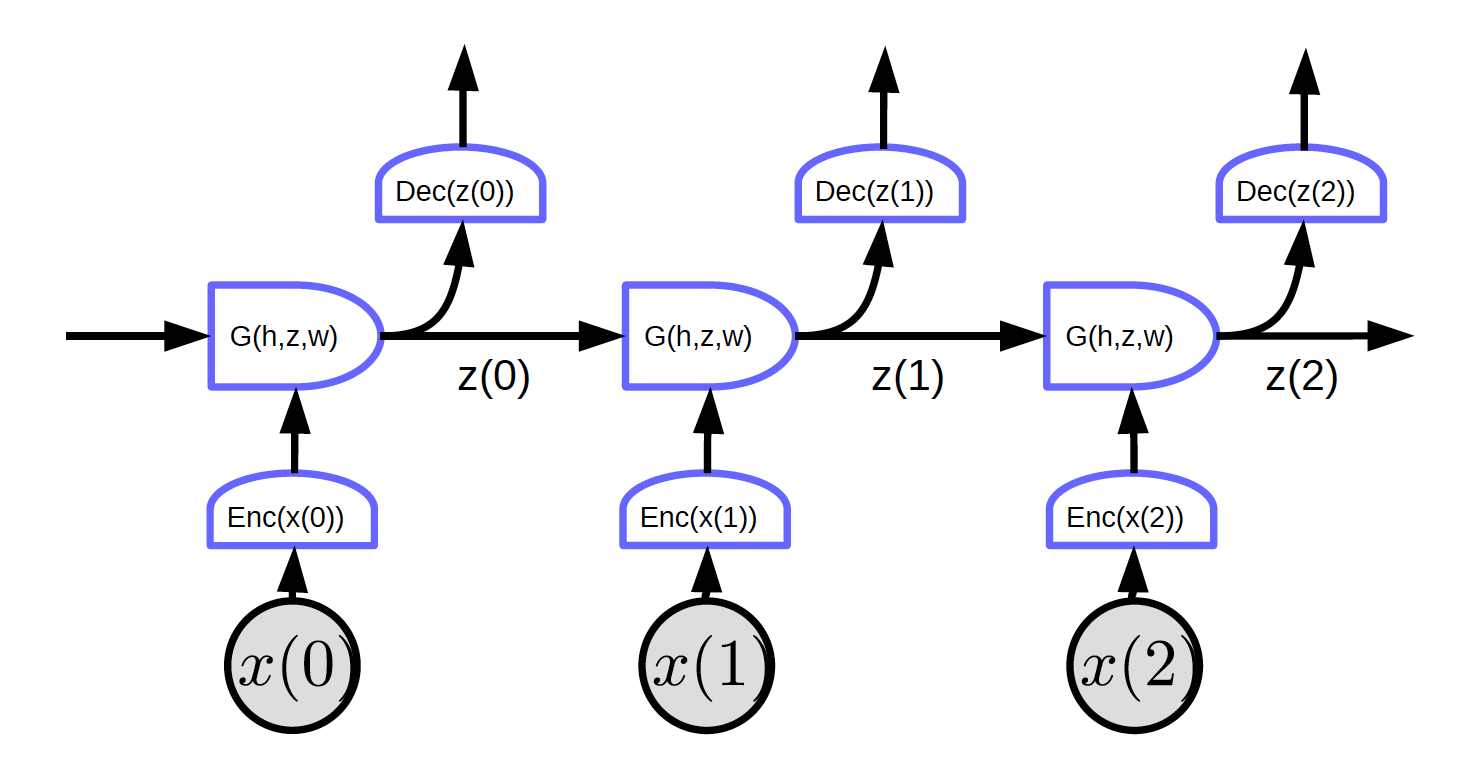
الشكل 1. إلتفاف الشبكات العصبية التكرارية

• $x(t)$: مدخل يتغير بمرور الوقت.
• $\text{Enc}(x(t))$: مشفِر يقوم بإنشاء تمثيل للمدخل.
• $h(t)$: تمثيل للمدخلات.
• $w$: معاملات قابلة للتدريب.
• $z(t-1)$: الحالة الخفية السابقة، وهي ناتج الخطوة الزمنية السابقة.
• $z(t)$: الحالة الخفية الحالية.
• $g$: دالة يمكن أن تكوِن شبكة عصبية معقدة؛ أحد المدخلات هو $z(t-1)$ وهو ناتج الخطوة الزمنية السابقة.
• $\text{Dec}(z(t))$: وحدة فك الترميز وهي تولِد المخرجات.

الشبكات العصبية التكرارية: فتح الحلقة

قم بفتح الحلقة بالنسبة للزمن. المدخل عبارة عن تسلسل x_T ,....,x_3 ,x_2 ,x_1

"
الشكل 2. شبكات عصبية تكرارية ذات حلقات مفتوحة

في شكل 2، المدخلات هي $x_1$، $x_2$، و $x_3$.

في الزمن $t=0$، يتم تمرير المدخل $x(0)$ إلى المشفِر ويولِد التمثيل $h(x(0)) = \text{Enc}(x(0))$ ثم يمرره إلى الدالة $G$ لإنشاء الحالة الخفية $z(0) = G(h_0, z’, w)$. عند $t=0$، يمكن تهيئة $z’$ في الدالة $G$ كـ $0$ أو تهيئته عشوائيًا. يتم تمرير $z(0)$ إلى مفكك الشفرة لتوليد مخرجات وكذلك توليد الخطوة الزمنية التالية.

نظرًا لعدم وجود حلقات في هذه الشبكة، يمكننا تنفيذ الانتشار العكسي.

يوضح الشكل 2 شبكة منتظمة بخاصية معينة: تشترك كل مجموعة في نفس الأوزان. ثلاثة مشفرات و وحدات فك التشفير و دوال $G$ لها نفس الأوزان على التوالي عبر خطوات زمنية مختلفة.

BPTT: الانتشار العكسي عبر الزمن (Backprop through time). للأسف، BPTT لا يعمل بشكل جيد في الشكل البسيط للـ RNN.

مشاكل نواجهها الـ RNNs:

1. تلاشي التدرجات
   • في تسلسل طويل، يتم ضرب التدرجات في (transpose أو منقول)مصفوفة الأوزان في كل خطوة زمنية. إذا كانت هناك قيم صغيرة في مصفوفة الوزن، فإن معيار (norm) التدرج يتقلص بمقدار أسي.
2. انفجار التدرجات
   • إذا كانت لدينا مصفوفة ذات أوزان كبيرة و اللاخطية في الطبقة التكرارية غير مشبعة، فسوف تنفجر التدرجات. سوف تتباعد الأوزان في كل خطوة. و قد نُضطر إلى استخدام معدل تعلم صغير حتى يعمل الانحدار التدريجي بشكل جيد.

أحد أسباب استخدام الـ RNNs هو ميزة تذكر المعلومات السابقة. ومع ذلك، قد تفشل RNN بسيطة في حفظ المعلومات لفترة طويلة دون بعض الحيل.

مثال لمشكلة التدرجات المتلاشية:

تمثل المدخلات رموزًا من برنامج بلغة C. سيحدد النظام ما إذا كان برنامجًا صحيحًا نحويًا أم لا. يجب أن يحتوي البرنامج الصحيح نحويًا على عدد صالح من الأقواس. و بالتالي، يجب أن تتذكر الشبكة عدد الأقواس والأقواس المفتوحة التي يجب التحقق منها، و ما إذا كنا قد أغلقناها جميعًها. يجب أيضا على الشبكة تخزين هذه المعلومات في حالات مخفية مثل العداد. ومع ذلك، و بسبب التدرجات المتلاشية، فإنها ستفشل في الحفاظ على هذه المعلومات في برنامج لمدة طويلة.

حيل للشبكات العصبية التكرارية

• قص التدرجات: (بغية تجنب انفجار التدرجات) اختزل التدرجات عندما تصبح كبيرة جدًا.

• التهيئة: (ابدأ عند المقدار الصحيح لتفادي انفجار/تلاشي التدرجات) تهيئة مصفوفات الأوزان للحفاظ على المعدل إلى حد ما. على سبيل المثال، تؤدي التهيئة المتعامِدة إلى تهيئة مصفوفة الأوزان كمصفوفة متعامدة عشوائية.

النماذج المضاعفة

في النماذج المضاعفة بدلاً من حساب فقط مجموع أوزان المدخلات، نقوم بحساب جداء المدخلات ثم نحسب مجموع أوزان ذلك.

نفترض أن $x \in {R}^{n\times1}$، $W \in {R}^{m \times n}$، $U \in {R}^{m \times n \times d}$، و $z \in {R}^{d\times1}$. هنا نجد أن $U$ عبارة عن موتر.

حيث: $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

مخرجات النظام عبارة عن المجموع الموزون المتعارف عليه للمدخلات والأوزان. الأوزان نفسها هي أيضًا مجموع موزون للأوزان والمدخلات.

معمارية الشبكة الفائقة: يتم حساب الأوزان بواسطة شبكة أخرى.

الانتباه

$x_1$ و $x_2$ عبارة عن متجهان، $w_1$ و $w_2$ هما كميتان قياسيتان بعد دخول دالة softmax حيث $w_1 + w_2 = 1$، و $w_1$ و $w_2$ تتراوح ما بين 0 و 1. $w_1x_1 + w_2x_2$ مجموع موزون لـ $x_1$ و $x_2$ و هو موزون بمعاملات $w_1$ و $w_2$.

من خلال تغيير الحجم النسبي لـ $w_1$ و $w_2$، يمكننا تغيير مُخرج $w_1x_1 + w_2x_2$ إلى $x_1$ أو $x_2$ أو بعض المجموعات الخطية من $x_1$ و $x_2$.

يمكن أن تحتوي المدخلات على متجهات $x$ متعددة (أكثر من $x_1$ و $x_2$). سيختار النظام مجموعة مناسبة، يتم تحديد اختيارها بواسطة متغير آخر $z$. تسمح آلية الانتباه للشبكة العصبية بتركيز انتباهها على مدخلات معينة وتجاهل الآخرين.

يتزايد الاهتمام بالانتباه في أنظمة الـ NLP التي تستخدم بنى المحولات أو أنواع انتباه أخرى.

الأوزان مستقلة عن البيانات لأن $z$ مستقلة عن البيانات.

وحدات البوابات المتكررة (GRU)

كما ذكرنا سابقًا، يعاني RNN من تلاشي/انفجار التدرجات ولا يمكنه تذكر الحالات لفترة طويلة جدًا. وحدات البوابات المتكررة Cho 2014، هو تطبيق للنماذج المضاعفة التي تحاول حل هذه المشكلات. إنه مثال لشبكة تكرارية مع ذاكرة (LSTM). يظهر هيكل الـ GRU أدناه:

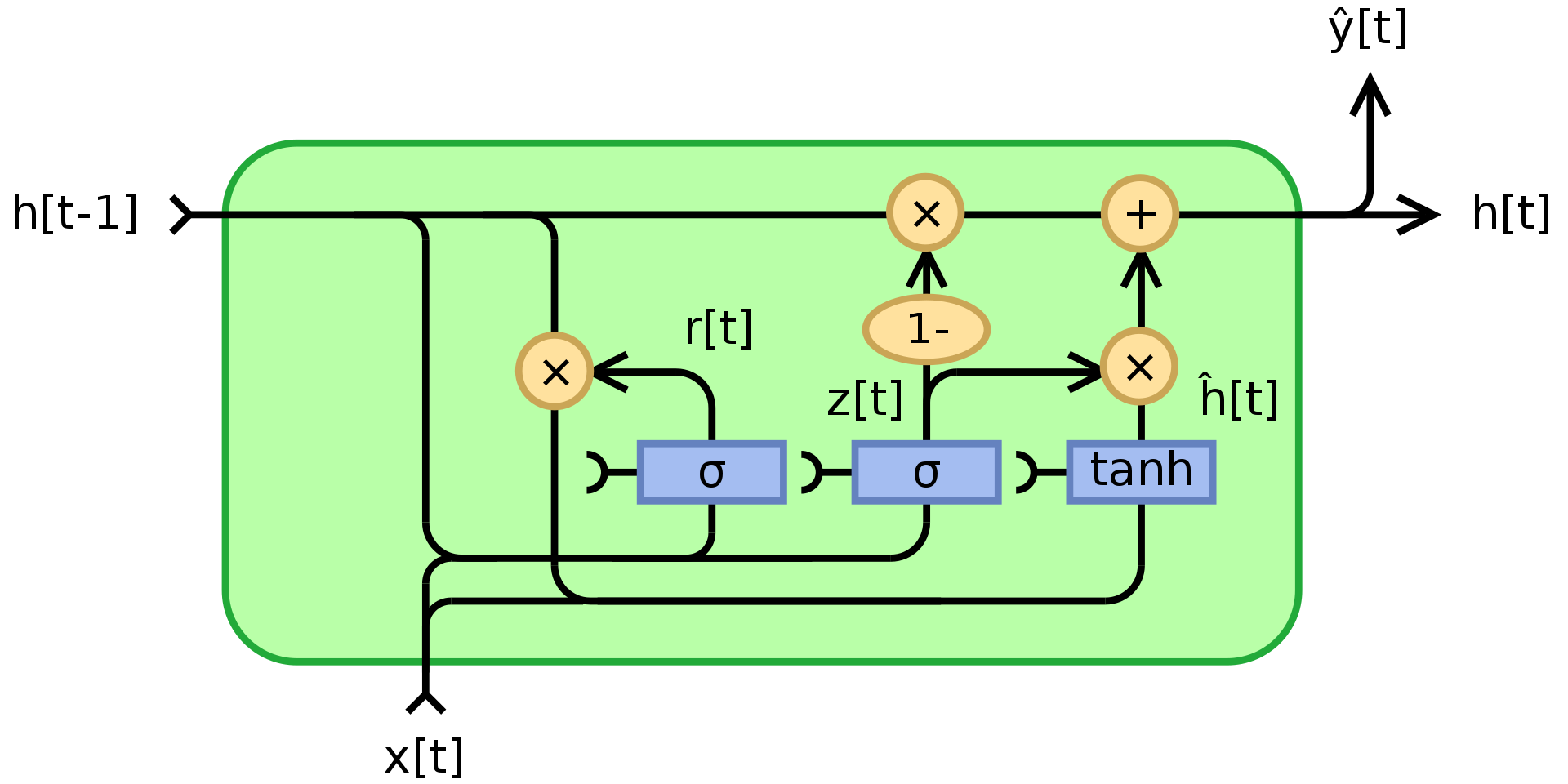
الشكل 3. وحدة البوابات المتكررة

حيث تشير $\odot$ إلى الضرب حسب العنصر (عملية ضرب Hadamard). $x_t$ هو متجه الإدخال، $h_t$ هو متجه الإخراج، $z_t$ هو متجه بوابة التحديث، $r_t$ هو متجه بوابة إعادة الضبط، $\phi_h$ هي دالة الظل الزائدي (tanh)، و $W$، $U$، $b$ هي معاملات قابلة للتعلم.

لأكون دقيقا، فإن $z_t$ عبارة عن متجه بوابة يحدد مقدار المعلومات السابقة التي يجب تمريرها إلى المستقبل. يطبق دالة sigmoid لمجموع طبقتين خطيتين و انحياز على المدخل $x_t$ والحالة السابقة $h_{t-1}$. يحتوي $z_t$ على معاملات بين 0 و 1 نتيجة لتطبيق دالة sigmoid. حالة الإخراج النهائية $h_t$ عبارة عن تركيبة محدبة من $h_{t-1}$ و $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ via $z_t$ عبر $z_t$. إذا كان المعامل يساوي 1، فإن ناتج الوحدة الحالية هو مجرد نسخة من الحالة السابقة و يتم تجاهل المدخلات (و هو السلوك الافتراضي). إذا كان المعامل أقل من واحد، فإنه يأخذ في الاعتبار بعض المعلومات الجديدة من المدخل.

يتم استخدام بوابة إعادة الضبط $r_t$ لتحديد مقدار المعلومات السابقة التي يجب التخلي عنها. في محتوى الذاكرة الجديد $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$، إذا كان معامل $r_t$ هو 0، فإنه لا يخزن أيًا من المعلومات السابقة. أما إذا كانت قيمة $z_t$ تساوي 0 في ذات الوقت، فسيتم إعادة ضبط النظام بالكامل لأن $h_t$ ستنظر فقط إلى المدخل.

LSTM (Long Short-Term Memory أو الذاكرة القصيرة المدى المطولة)

GRU هي في الواقع نسخة مبسطة من الـ LSTM والتي ظهرت قبل ذلك بكثير، Hochreiter، Schmidhuber، 1997. من خلال بناء خلايا الذاكرة للحفاظ على المعلومات السابقة، تهدف LSTM أيضًا إلى حل مشكلة فقدان الذاكرة على المدى الطويل في RNNs. يظهر هيكل LSTM أدناه:

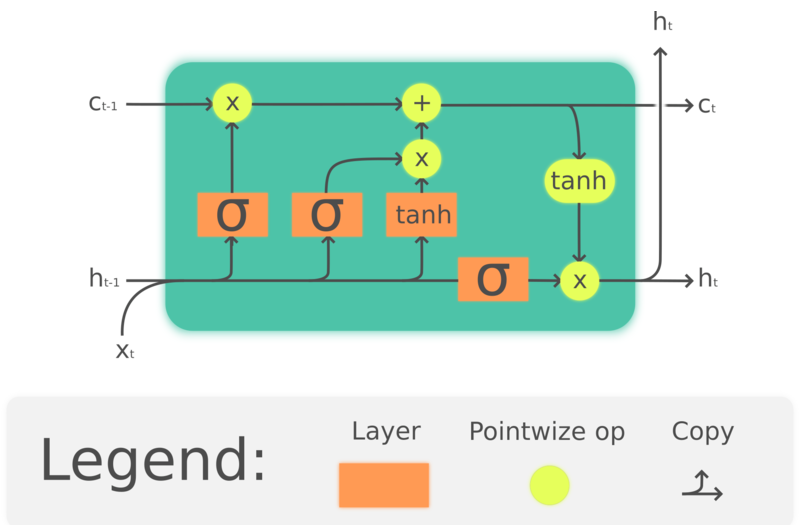
الشكل 4. LSTM

حيث تشير $\odot$ إلى الضرب بالعنصر، $x_t\in\mathbb{R}^a$ هو متجه المدخل إلى وحدة الـ LSTM، $f_t\in\mathbb{R}^h$ هو متجه تنشيط بوابة النسيان، $i_t\in\mathbb{R}^h$ هو متجه تنشيط بوابة الإدخال/التحديث، $o_t\in\mathbb{R}^h$ هو متجه تنشيط بوابة الإخراج، $h_t\in\mathbb{R}^h$ هو متجه الحالة الخفية (المعروف أيضًا باسم الإخراج)، $c_t\in\mathbb{R}^h$ هو متجه حالة الخلية.

تستخدم وحدة LSTM حالة الخلية $c_t$ لنقل المعلومات من خلال الوحدة. ينظم كيفية حفظ المعلومات أو إزالتها من حالة الخلية من خلال هياكل تسمى البوابات. تحدد بوابة النسيان $f_t$ مقدار المعلومات التي نريد الاحتفاظ بها من حالة الخلية السابقة $c_{t-1}$ وذلك بالنظر إلى المدخلات الحالية والحالة الخفية السابقة، وتنتج رقمًا بين 0 و 1 كمعامل $c_{t-1}$. $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ يحسب مرشحًا جديدًا لتحديث حالة الخلية، ومثل بوابة النسيان، تحدد بوابة الإدخال $i_t$ مقدار التحديث الذي سيتم تطبيقه. أخيرًا، سيعتمد الإخراج $h_t$ على حالة الخلية $c_t$، ولكن سيتم تمريره عبر دالة الـ $\tanh$ ثم تصفيته بواسطة بوابة الإخراج $o_t$.

على الرغم من أن LSTM تُستخدَم على نطاق واسع في الـ NLP، إلا أن شعبيتها آخذة في التناقص شيئا فشيئا. على سبيل المثال، يتجه التعرف على الكلام نحو استخدام CNN زمنية، ويتجه مجال الـ NLP نحو استخدام المحولات.

نموذج تسلسل إلى تسلسل (Seq2Seq)

النهج الذي اقترحه Sutskever NIPS 2014 هو أول نظام آلي عصبي للترجمة له أداء مشابه للأنظمة الكلاسيكية. فهو يستخدم معمارية التشفير و فك التشفير حيث يكون كل من المشفر و وحدة فك التشفير عبارة عن شبكة LSTM متعددة الطبقات.

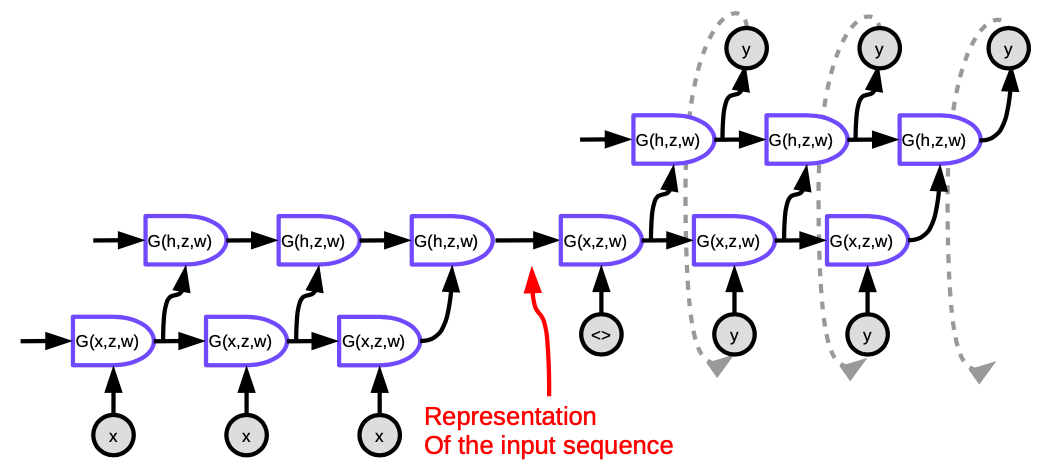
الشكل 5. Seq2Seq

كل خلية في الشكل هي LSTM. بالنسبة لبرنامج التشفير (الجزء الموجود على اليسار)، فإن عدد الخطوات الزمنية يساوي طول الجملة المراد ترجمتها. في كل خطوة، توجد مجموعة من LSTMs (أربع طبقات في هذه الورقة) حيث يتم تمرير الحالة الخفية للـ LSTM السابقة إلى المرحلة التالية. مخرجات الطبقة الأخيرة في الخطوة الزمنية الأخيرة عبارة عن متجهٍ يمثل معنى الجملة بأكملها، والتي يتم إدخالها بعد ذلك في LSTM أخرى متعددة الطبقات (وحدة فك التشفير)، والتي تنتج كلمات في اللغة المراد الترجمة إليها. في وحدة فك التشفير، يتم إنشاء النص بطريقة متسلسلة. تنتج كل خطوة كلمة واحدة يتم تغذيتها كمدخل للخطوة الزمنية التالية.

هذه المعمارية غير مرضية من ناحيتين: أولاً، يجب تلخيص المعنى الكامل للجملة في الحالة الخفية بين المشفر و وحدة فك التشفير. ثانيًا، لا تحتفظ شبكات LSTMs بالمعلومات لأكثر من 20 كلمة تقريبًا. يتم إصلاح هذه المشكلات بواسطة Bi-LSTM، والذي يقوم بتشغيل وحدتي LSTM في اتجاهين متعاكسين. في Bi-LSTM يتم ترميز المعنى في متجهين، أحدهما يتم إنشاؤه عن طريق تشغيل LSTM من اليسار إلى اليمين، والآخر من اليمين إلى اليسار. هذا يسمح بمضاعفة طول الجملة دون فقدان الكثير من المعلومات.

Seq2seq مع الانتباه

كان نجاح النظام أعلاه قصير الأجل. حيث اقترح بحث آخر بقلم Bahdanau، Cho، و Bengio أنه بدلاً من وجود شبكة عملاقة تختصر معنى الجملة بأكملها في متجه واحد، سيكون من المنطقي أكثر إذا ركزنا الانتباه فقط في كل خطوة على المواقع ذات الصلة في لغة النص الأصلي و ذات معنى مكافئ، أي آلية الانتباه.

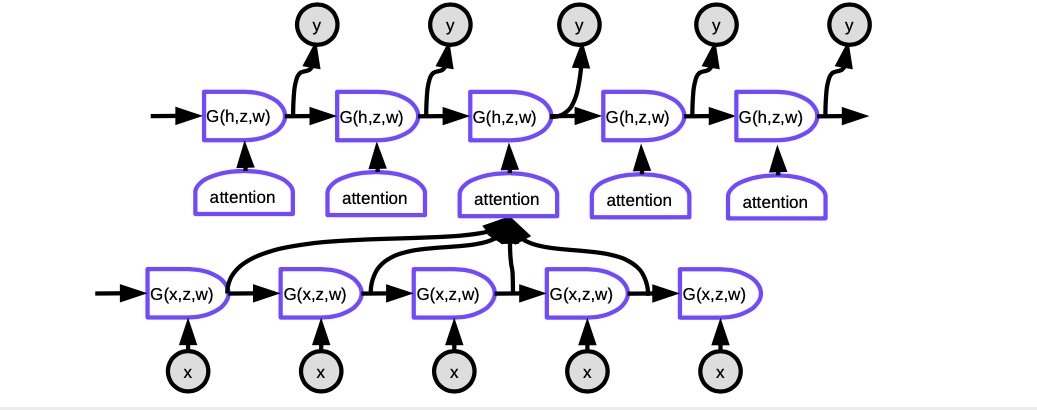
الشكل 6. Seq2Seq مع الانتباه

في آلية الانتباه، لإنتاج الكلمة الحالية في كل خطوة زمنية، نحتاج أولاً إلى تحديد التمثيلات الخفية للكلمات في الجملة المدخلة التي يجب التركيز عليها. بشكل أساسي، ستتعلم الشبكة تسجيل مدى تطابق كل مدخل مشفر مع المخرج الحالي لوحدة فك التشفير. يتم تسوية هذه المخرجات بواسطة softmax، ثم يتم استخدام المعاملات لحساب مجموع موزون للحالات الخفية في المشفر في خطوات زمنية مختلفة. من خلال ضبط الأوزان، يمكن للنظام تعديل منطقة المدخلات التي يجب التركيز عليها. سحر هذه الآلية هو أن الشبكة المستخدمة لحساب المعاملات يمكن تدريبها بواسطة الانتشار الخلفي. ليست هناك حاجة لبنائها يدويا!

غيرت آليات الانتباه من الترجمة الآلية العصبية تمامًا. في وقت لاحق، نشرت Google ورقة بحثية تحت عنوان “الانتباه هو كل ما تحتاجه” “ Attention Is All You Need“، ووضعوا فيها المحولات الأمامية (forward transformer)، حيث تقوم كل طبقة و مجموعة من الخلايا العصبية بتنفيذ الانتباه.

شبكة الذاكرة

نبعت فكرة شبكات الذاكرة من العمل في Facebook الذي بدأه Antoine Bordes في عام 2014 و Sainbayar Sukhbaatar في عام 2015.

فكرة شبكة الذاكرة هي أن هناك جزئين مهمين في دماغك: أحدهما هو القشرة (cortex)، حيث يكون لديك ذاكرة طويلة المدى. هناك قطعة منفصلة أخرى من الخلايا العصبية تسمى الحُصين (hippocampus) و التي ترسل إشارات إلى كل مكان تقريبًا في القشرة. يُعتقد أن الحُصين يُستخدم للذاكرة قصيرة المدى، وتذكر الأشياء لفترة قصيرة نسبيًا. النظرية السائدة هي أنه عندما تنام، يتم نقل الكثير من المعلومات من الحُصين إلى القشرة ليتم ترسيخها في الذاكرة طويلة المدى لأن الحُصين له سعة محدودة.

بالنسبة لشبكة الذاكرة، يوجد مدخل للشبكة، $x$ (فكر في الأمر كموقع في الذاكرة) و قارن هذا المتجه $x$ بالمتجهات $k_1, k_2, k_3, \cdots$ (“المفاتيح”) باستخدام الضرب نقطي. ضعهم في دالة softmax، وستحصل على مجموعة من الأرقام التي مجموعها يساوي واحد. وهناك مجموعة من المتجهات الأخرى $v_1, v_2, v_3, \cdots$ (“القيم”). اضرب هذه المتجهات بالأعداد من دالة الـ softmax و قم بجمع هذه المتجهات لتحصل على النتيجة (لاحظ التشابه مع آلية الانتباه).

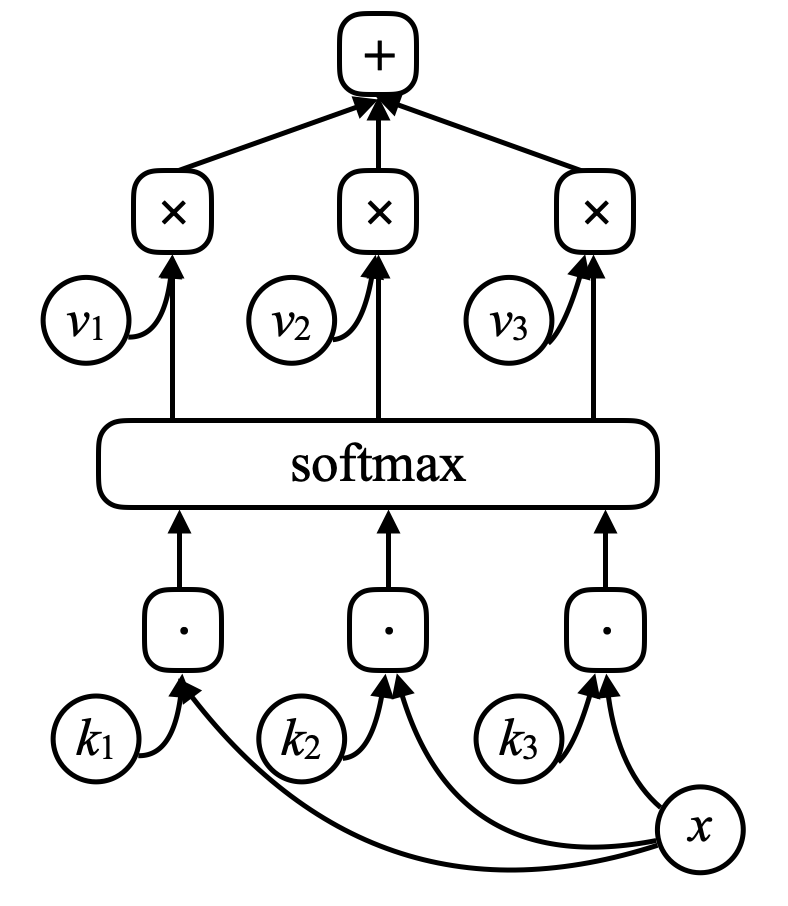
الشكل 7. شبكة الذاكرة

إذا تطابق أحد المفاتيح (مثلاً، $k_i$) تمامًا مع $x$، فسيكون المعامل المرتبط بهذا المفتاح قريبًا جدًا من واحد. لذلك سيكون ناتج النظام أساسًا $v_i$.

إنها ذاكرة ارتباطية معنونة. الذاكرة الارتباطية هي أنه إذا تطابقت مدخلاتك مع مفتاح، تحصل على تلك القيمة. وهذه هي مجرد نسخة سهلة التفاضل منها، و التي تسمح لك بإلانتشار الخلفي وتغيير المتجهات من خلال الانحدار التدريجي.

ما فعله المؤلفون هو سرد قصة لنظام من خلال إعطائه سلسلة من الجمل. يتم ترميز الجمل في متجهات عن طريق تمريرها عبر شبكة عصبية لم يتم تمرينها مسبقًا. يتم إرجاع الجمل إلى الذاكرة. عندما تطرح سؤالاً على النظام، تقوم بتشفير السؤال وتضعه كمدخل للشبكة العصبية، و تنتج الشبكة العصبية متغير $x$ في الذاكرة، فتعيد الذاكرة قيمة ما.

تُستخدم هذه القيمة، بالإضافة إلى الحالة السابقة للشبكة، لإعادة الوصول إلى الذاكرة. وتقوم بتدريب هذه الشبكة بأكملها للحصول على جواب لسؤالك. بعد تدريب مكثف، يتعلم هذا النموذج بالفعل تخزين القصص و الإجابة على الأسئلة.

في شبكة الذاكرة، توجد شبكة عصبية تأخذ مدخلاً ثم تنتج عنوانًا أو موقعًا في الذاكرة، وتستعيد قيمته إلى الشبكة، و تستمر هكذا إلى أن تُنتِج مخرجات في النهاية. يشبه هذا الكمبيوتر إلى حد كبير، عند وجود وحدة معالجة مركزية و ذاكرة خارجية للقراءة و الكتابة.

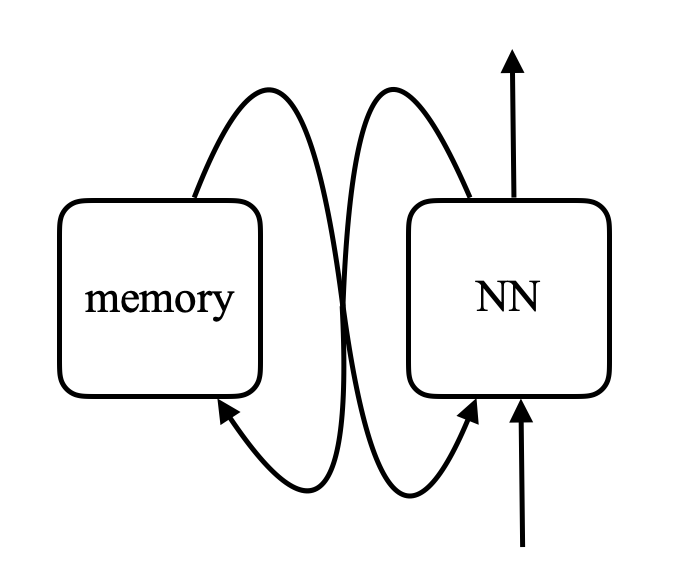
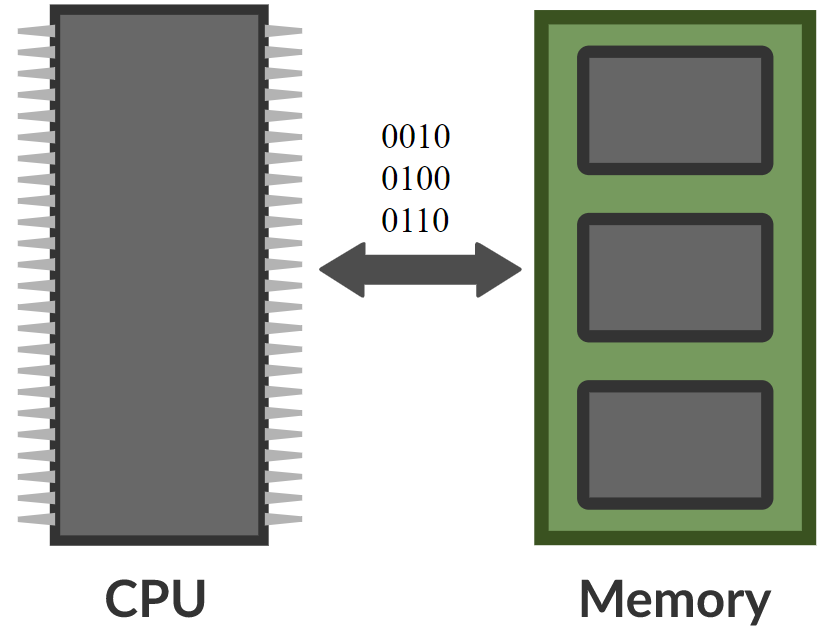
الشكل 8. مقارنة بين شبكة الذاكرة و الكمبيوتر (الصورة من Khan Acadamy)

هناك أشخاص تخيلوا أنه يمكن بالفعل بناء حاسبات اشتقاقية بناءً على هذا. أحد الأمثلة على ذلك هو آلة تورنغ العصبية من DeepMind، والتي تم جعلها متاحة للعامة بعد ثلاثة أيام من نشر Facebook لورقة علمية على الـ arXiv.

الفكرة هي مقارنة المدخلات بالمفاتيح، وتوليد المعاملات، وإنتاج القيم - والتي تمثل أساسًا المحول. المحول هو في الأساس شبكة عصبية تكون فيها كل مجموعة من الخلايا العصبية واحدة من هذه الشبكات.