تطبيقات الشبكات الالتفافية

التعرف على الرمز البريدي

في الدرس السابق، أوضحنا كيف يمكن للشبكات الالتفافية التعرف على الأرقام، لكننا لم نجب على سؤال كيف يمكن للنموذج معرفة الارتباك الناجم عن الأرقام المجاورة له عند اختيار كل رقم. تتمثل الخطوة التالية في اكتشاف الكائنات المتداخلة / غير المتداخلة واستخدام نهج ((Non-Maximum Supression (NMS) بالنظر إلى افتراض أن المدخلات عبارة عن أرقام غير متداخلة في هذا المثال، فإن الاستراتيجية التي يجب اتباعها هي تدريب شبكات الالتفافية متعددة واختيار الرقم الحاصل على أعلى الدرجات الناتجة عن الشبكة أو عن طريق التصويت بالأغلبية.

CNN التعرف بواسطة

نقدم هنا مهمة التعرف على الرموز البريدية غير المتداخلة المكونة من خمسة أرقام. لم يتم إعطاء النظام تعليمات حول كيفية فصل كل رقم، لكن النظام يعرف أنه يجب عليه تقدير خمسة أرقام. كما هو موضح في (الشكل 1)، يتكون النظام من شبكات الالتفافية بـ 4 أبعاد مختلفة، ينتج كل منها مخرجات مختلفة. تظهر المخرجات على شكل مصفوفة. تأتي مصفوفات الإخراج الأربع من نماذج ذات عروض نواة مختلفة في الطبقة الأخيرة. يحتوي كل ناتج على 10 صفوف تمثل 10 فئات من 0 إلى 9. يمثل المربع الأبيض الأكبر درجة أعلى في تلك الفئة. في كتل الإخراج الأربعة هذه، تكون أبعاد نوى الطبقة الأخيرة على المحور الأفقي هي 5 و 4 و 3 و 2 على التوالي. يحدد حجم النواة عرض النافذة التي ينظر النموذج من خلالها إلى المدخلات. ثم يختار النموذج الفئة التي حصلت على أعلى الدرجات في تلك النافذة. يأخذ النموذج بعد ذلك تصويت الأغلبية لاستخراج معلومات مفيدة، يجب على المرء أن يضع في اعتباره أنه ليست كل مجموعات الأحرف ممكنة، وبالتالي يمكن تصحيح تلك الأخطاء بفرض قيود على المدخلات للتأكد من أن المخرجات هي الرموز البريدية الصحيحة.

الشكل 1 : مصنفات متعددة للتعرف على الرمز البريدي

الحيلة هي استخدام أقصر خوارزمية مسار لتحديد ترتيب الأحرف. نظرًا لأننا نعرف فترات الأحرف المحتملة وعدد الأرقام الإجمالي التي نحتاج إلى التنبؤ بها، يمكننا التعامل مع هذه المشكلة من خلال حساب الحد الأدنى لتكلفة الأرقام و الانتقال بينها. يجب أن يكون المسار مستمراً من الخلية اليسرى السفلية إلى الخلية اليمنى العلوية على الرسم البياني ويجب أن يكون مقيدًا ليشمل حركات معينة من اليمين إلى اليسار، ومن أعلى إلى أسفل. لاحظ أنه في حالة تكرار نفس الأرقام جنبًا إلى جنب، يجب أن تكون الخوارزمية قادرة على التمييز بين هذه الأرقام كأرقام متكررة بدلاً من تخمينها بأرقام فردية.

التعرف على الوجه

تعمل الشبكات العصبية الالتفافية بشكل جيد في مهام الكشف ولا يعد الكشف عن الوجوه استثناءً. لإجراء التعرف على الوجوه، نحتاج إلى إنشاء مجموعة بيانات من الصور الوجوه و أخرى بدونها، حيث سنقوم بتدريب شبكة الالتفافية، ونسأل عما إذا كان المدخل إلى الشبكة يحتوي على وجه. عندما نطبق النموذج على صورة جديدة بعد التدريب، إذا كان هناك وجه فسوف تتوهج الشبكة الالتفافية في المواضع المقابلة. ومع ذلك، هناك مشكلتان:

• الموجب المزيف: هناك العديد من الأشكال المختلفة التي لا تعد وجهًا والتي قد تظهر في رقعة من الصورة. خلال مرحلة التدريب، قد لا يرى النموذج كل منهم (أي مجموعة تمثيلية بالكامل من الرقع التي لا تمثل الوجه). لذلك، قد يعاني النموذج من الكثير من الإيجابيات الخاطئة في وقت الاختبار. على سبيل المثال، إذا لم يتم تدريب الشبكة على الصور التي تحتوي على الأيدي، فقد تكتشف الوجوه بناءً على درجات لون البشرة وتصنف بشكل غير صحيح بقع من الصور التي تحتوي على الأيدي كوجوه، مما يؤدي إلى ظهور إيجابيات زائفة.

• اختلاف حجم الوجوه: ليست كل الوجوه بحجم 30 $\times$ 30 من البيكسلات لذلك قد لا يتم اكتشاف الوجوه ذات الأحجام المختلفة. تتمثل إحدى طرق التعامل مع هذه المشكلة في إنشاء إصدارات متعددة المقاييس من نفس الصورة. سيكتشف النموذج الأساسي الوجوه التي تتراوح أحجامها حول 30 $\times$ 30 بيكسل. في حالة تطبيق مقياس على صورة بعامل $\sqrt 2$، سيكتشف النموذج الوجوه الأصغر في الصورة الأصلية، وذلك لأن الأبعاد التي كانت في السابق 30 $\times$ 30 قد أصبحت 20 $\times$ 20 بيكسل. لاكتشاف الوجوه الأكبر، يمكننا تصغير حجم الصورة. هذه العملية غير مكلفة لأن نصف النفقات تأتي من معالجة الصورة الأصلية غير المقاسة. مجموع نفقات جميع الشبكات الأخرى مجتمعة هو نفسه تقريبًا مثل معالجة الصورة الأصلية غير المقاسة. حجم الشبكة هو مربع حجم الصورة على جانب واحد، لذلك إذا قمت بتصغير الصورة $\sqrt 2$، فإن الشبكة التي تحتاج إلى تشغيلها تكون أصغر بمعامل 2. وبالتالي فإن التكلفة الإجمالية هي $1+1/2+1/4+1/8+1/16…$، والذي يساوي 2. أداء نموذج متعدد المقاييس يضاعف فقط التكلفة الحسابية.

نظام كشف الوجوه متعدد المقاييس

الشكل 2: نظام الكشف عن الوجه

تشير الخرائط الموضحة في (الشكل 3) إلى نتائج كاشفات الأوجه. يتعرف كاشف الوجه هذا على الوجوه التي يبلغ حجمها 20 $\times$ 20 بكسل. في المقياس الدقيق (المقياس 3) هناك العديد من الدرجات العالية ولكنها ليست نهائية للغاية. عندما يرتفع عامل التحجيم (المقياس 6)، نرى المزيد من المناطق البيضاء المتجمعة. تمثل تلك المناطق البيضاء الوجوه المكتشفة. نطبق بعد ذلك إخماد القيم الدنيا للحصول على الموقع النهائي للوجه.

الشكل 3: درجات كشف الوجه لمعايير التحجيم المختلفة

إخماد القيم الدنيا (Non-maximum suppression)

لكل منطقة بقيم عالية، من المحتمل أن يكون عندها وجه. إذا تم اكتشاف المزيد من الوجوه بالقرب من الأول، فهذا يعني أنه يجب اعتبار وجه واحد فقط صحيحًا والباقي خاطئ. مع خوارزمية إخماد القيم الدنيا نأخذ أعلى درجات للمربعات المحيطة المتداخلة ونزيل المربعات الأخرى. ستكون النتيجة إحاطة مربع واحد في الموقع الأمثل.

التعدين السلبي (Negative Mining)

في القسم الأخير، ناقشنا كيف يمكن أن يواجه النموذج عددًا كبيرًا من الإيجابيات الخاطئة في وقت الاختبار حيث توجد العديد من الطرق التي تظهر الأشكال التي لا تعد وجوهًا بشكل مشابه للوجه. لن تتضمن أي مجموعة تدريب جميع الممكنة لهذه الأشكال المشابهة للوجوه ولكن لا تعد وجهًا. يمكننا تخفيف هذه المشكلة من خلال التعدين السلبي. في التعدين السلبي، نقوم بإنشاء مجموعة بيانات سلبية عبارة عن رقع لا تمثل وجوهًا والتي اكتشفها النموذج (خطأ) كوجوه. يتم جمع البيانات عن طريق تشغيل النموذج على المدخلات المعروف أنها لا تحتوي على وجوه. ثم نقوم بإعادة تدريب الكاشف باستخدام مجموعة البيانات السلبية. يمكننا تكرار هذه العملية لزيادة دقة (robustness) نموذجنا ضد الإيجابيات الزائفة.

التجزئة الدلالية (Semantic segmentation)

التجزئة الدلالية هي مهمة تعيين فئة لكل بكسل في صورة الإدخال.

الشبكات العصبية الالتفافية لرؤية الروبوتات التكيفية طويلة المدى

في هذا المشروع، كان الهدف هو تسمية المناطق من الصور المدخلة حتى يتمكن الروبوت من التمييز بين الطرق والعقبات. في الشكل، المناطق الخضراء هي مناطق يمكن للروبوت أن يقود عليها والمناطق الحمراء تمثل عوائق مثل العشب الطويل. لتدريب الشبكة على هذه المهمة، أخذنا رقعة من الصورة وقمنا يدويًا بتسميتها بأنها قابل للعبور أو لا (أخضر أو أحمر). ثم نقوم بتدريب الشبكة الالتفافية على الرقع من خلال مطالبتها بالتنبؤ بلون الرقعة. بمجرد أن يتم تدريب النظام بشكل كافٍ، يتم تطبيقه على الصورة بأكملها، مع تسمية جميع مناطق الصورة باللون الأخضر أو الأحمر.

الشكل 4: الشبكات العصبية الالتفافية لرؤية الروبوتات التكيفية طويلة المدى

كانت هناك خمس فئات للتنبؤ: 1) الأخضر الفائق، 2) الأخضر، 3) الأرجواني: خط يوضح حدود العائق، 4) العائق الأحمر 5) الأحمر الفائق: بالتأكيد عقبة.

تسميات ستيريو (الشكل 4, العمود 2) يتم التقاط الصور بالكاميرات الأربع الموجودة على الروبوت، والتي تم تجميعها كزوحين من رؤية ستريو. باستخدام المسافات المعروفة بين الكاميرات الاستريو المزدوجة، يتم بعد ذلك تقدير مواضع كل بكسل في الفضاء ثلاثي الأبعاد عن طريق قياس المسافات النسبية بين وحدات البكسل التي تظهر في كلتا الكاميرتين في زوج استريو. هذه هي نفس العملية التي تستخدمها أدمغتنا لتقدير مسافة الأشياء التي نراها. باستخدام معلومات الموقع المقدرة، يتلاءم المستوى مع الأرض، ثم يتم تصنيف وحدات البكسل على أنها خضراء إذا كانت بالقرب من الأرض والأحمر إذا كانت فوقها.

• القيود والمحفزات للـ ConvNet: تعمل الرؤية المجسمة فقط حتى 10 أمتار وتتطلب قيادة الروبوت رؤية بعيدة المدى. ومع ذلك، فإن الشبكة الالتفافية قادرة على اكتشاف الأشياء على مسافات أكبر بكثير، إذا تم تدريبها بشكل صحيح.

الشكل 5: هرم الحجوم الثابتة للصور المقاسة عن بعد

• توظيف كمدخلات للنموذج: تتضمن المعالجة المسبقة المهمة بناء هرم الحجوم الثابتة للصور المقاسة عن بعد (شكل 5). إنه مشابه لما فعلناه في وقت سابق من هذه المحاضرة عندما حاولنا اكتشاف الوجوه ذات المقاييس المتعددة.

مخرجات النموذج (الشكل 4، العمود 3)

يقوم النموذج بإخراج تسمية لكل بكسل في الصورة حتى الأفق. هذه هي مخرجات المصنف للشبكة الالتفافية متعددة المقاييس.

• كيف يصبح النموذج قابلاً للتكيف: تتمتع الروبوتات بوصول مستمر إلى تسميات الاستريو، مما يسمح للشبكة بإعادة التدريب والتكيف مع البيئة الجديدة التي توجد بها. يرجى ملاحظة أنه سيتم إعادة تدريب الطبقة الأخيرة فقط من الشبكة. يتم تدريب الطبقات السابقة في المعمل وتثبيتها.

أداء النظام

عند محاولة الوصول إلى إحداثيات GPS على الجانب الآخر من الحاجز، الروبوت “رأى” الحاجز من بعيد وخطط لطريق كي يتجنبه. هذا بفضل شبكة CNN التي تقوم باكتشاف الأجسام على بعد 50-100 متر.

قيود

رجوعا إلى 2000s، كانت الموارد الحاسوبية محدودة. كان الروبوت حينها قادرًا على معالجة حوالي صورة أو ما يعرف بإطار واحد فقط في الثانية، مما يعني أنه لن يكون قادرًا على اكتشاف شخص يسير في طريقه لمدة ثانية كاملة قبل أن يكون قادرًا على الرد. الحل لهذا الضغف هو بناء نموذج لتقدير التغير في موقع الروبوت بتكلفة منخفضة. فلا يعتمد على الشبكات العصبية، وله مسافة رؤية تتراوح حول 2.5 متر تقريبًا ولكنه قادر على الاستجابة بسرعة.

تحليل المشهد و وضع الأسماء

في هذه المهمة، يُخرج النموذج فئة الكائن (مبنى، سيارة، سماء، إلخ) لكل بكسل. تكون المعمارية أيضًا متعددة المقاييس (الشكل 6).

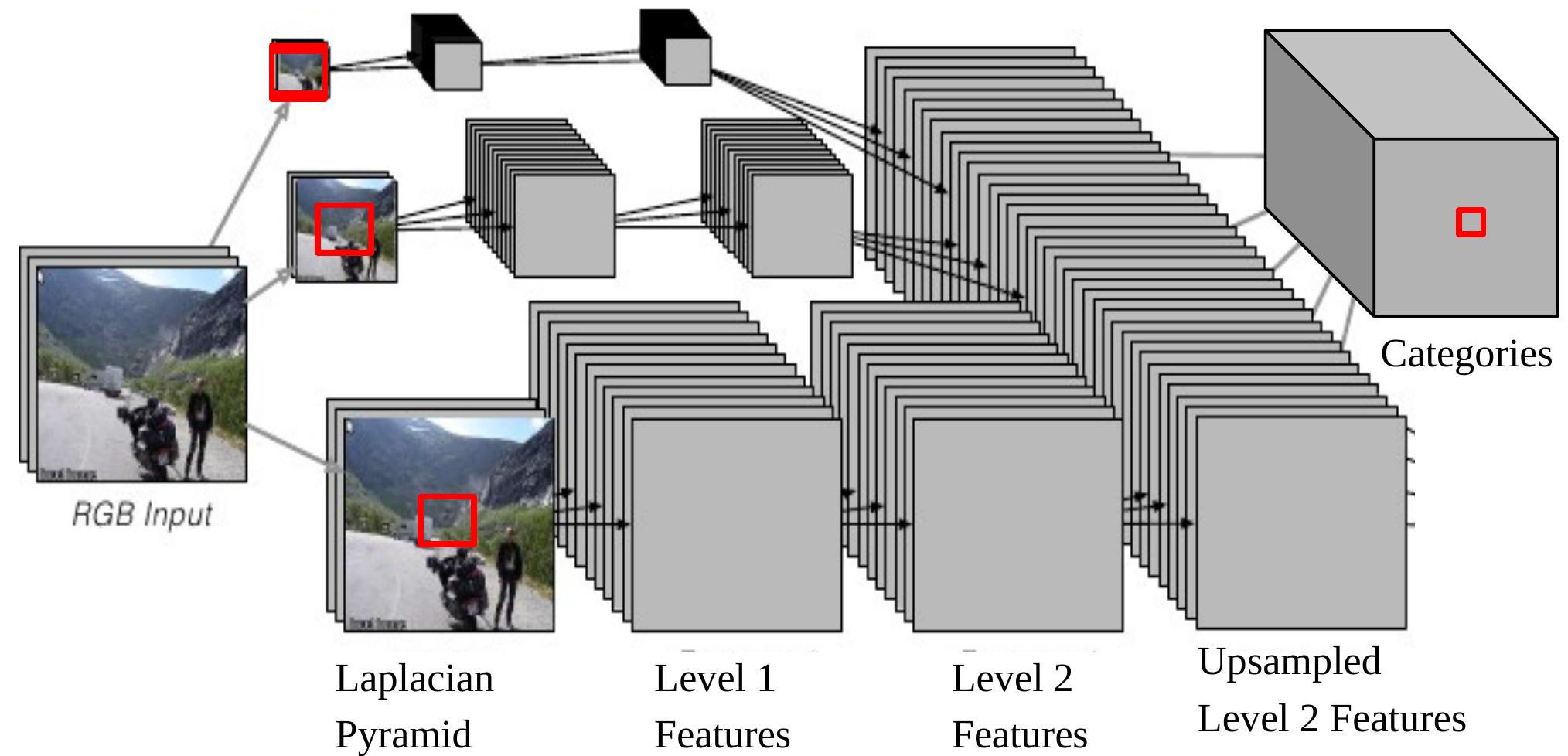
الشكل 6:شبكة عصبية إلتفافية متعددة المقاييس لتحليل المشاهد

لاحظ أنه إذا قمنا بإعادة عرض مخرج واحد من الـ CNN على المدخلات، فإنه يتوافق مع مدخل بحجم $46\times46$ على الصورة الأصلية في أسفل هرم لابلاس. هذا يعني أننا نستخدم سياق 46 × 46 بكسل لتحديد فئة البكسل المركزي.

ومع ذلك، أحيانًا لا يكون حجم هذا السياق كافيًا لتحديد فئة كائنات أكبر.

يتيح النهج متعدد النطاقات رؤية أوسع من خلال توفير صور إضافية تم إعادة قياسها كمدخلات. والخطوات هي كما يلي:

1. خذ نفس الصورة، قلص حجمها بمعامل 2 ثم معامل 4، كل على حدة.
2. يتم تغذية هاتين الصورتين الإضافيتين المعاد تحجيمهما إلى نفس الـ ConvNet (نفس الأوزان ونفس الأنوية) ونحصل على مجموعتين أخريين من خصائص المستوى 2.
3. قم بتكبير (Upsample) هذه الخصائص بحيث يكون لها نفس حجم خصائص المستوى 2 للصورة الأصلية.
4. كدس المجموعات الثلاث من الخصائص بعد التكبير معًا ثم قم بتغذيتها للمصنف.

الآن أكبر حجم فعال للمحتوى، والذي يأتي من الصورة التي تم تغيير حجمها بمقذار 1/4، هو $184\times 184\, (46\times 4=184)$.

الأداء: مع عدم وجود معالجة لاحقة وتشغيل إطار بإطار، يعمل النموذج بسرعة كبيرة حتى على الأجهزة العادية. يحتوي النموذج على حجم صغير إلى حد ما من بيانات التدريب (2k ~ 3k)، لكن النتائج لا تزال تحطم أرقامًا قياسية.