تقنيات التحسين الجزء الثاني
🎙️ Aaron Defazio(Adaptive methods) الطرق التَكَيُّفية
حاليا طريقة SGD مع الزخم هي أفضل طرق التحسين لكثير من مشاكل تعلم الآلة. لكن هنالك طرق أخرى مفيدة - يطلق عليها الطرق التَكَيُّفية و تم تطويرها عبر السنين - تساعد في التعامل مع المشاكل الصعبة والتي لا تنجح طريقة SGD في حلها.
في طريقة SGD فإن كل وزن في الشبكة يتم تحديثه باستخدام معادلة بمعدل تعلم ثابت ($\gamma$). لكن في الطرق التَكَيُّفية فيتم تكييف معدل تعلم لكل وزن. لهذا السبب فإننا نستخدم المعلومات التي نحصل عليها من إنحدار كل وزن.
عملياً يختلف هيكل الشبكات في الأغلب تكون في مختلف أجزاءها. مثلاً، قد تتكون الأجزاء الأولى من الشبكات العصبية الإلتفافية (CNN) من طبقات إلتفافية عدد قنواتها قليل وأبعاد كبيرة للقناة ولكن في الأجزاء الأخيرة قد تكون الطبقات ذات قنوات أكثر ولكن بأبعاد أصغر. فالعمليات تكون مختلقة في مختلف أجزاء الشبكة، لذلك فإن معدل التعلم قد يكون مناسب للأجزاء الأولى و غير مناسب للأجزاء الأخيرة. و هذا يعني أن استخدام معدلات تعلم تَكَيُّفية قد يكون أمرًا مفيدًا.
الأوزان في الأجزاء الأخيرة من الشبكة (4096 في الشكل رقم 1) لها تأثير كبير على مخرجات الشبكة. لذلك نحتاج إلى معدل تعلم صغير لهذه الأجزاء. في المقابل فإن الأوزان في الأجزاء الأولى يكون تأثيرها صغير على مخرجات الشبكة خصوصاً عندما يتم تهيأتها بأوزان عشوائية.
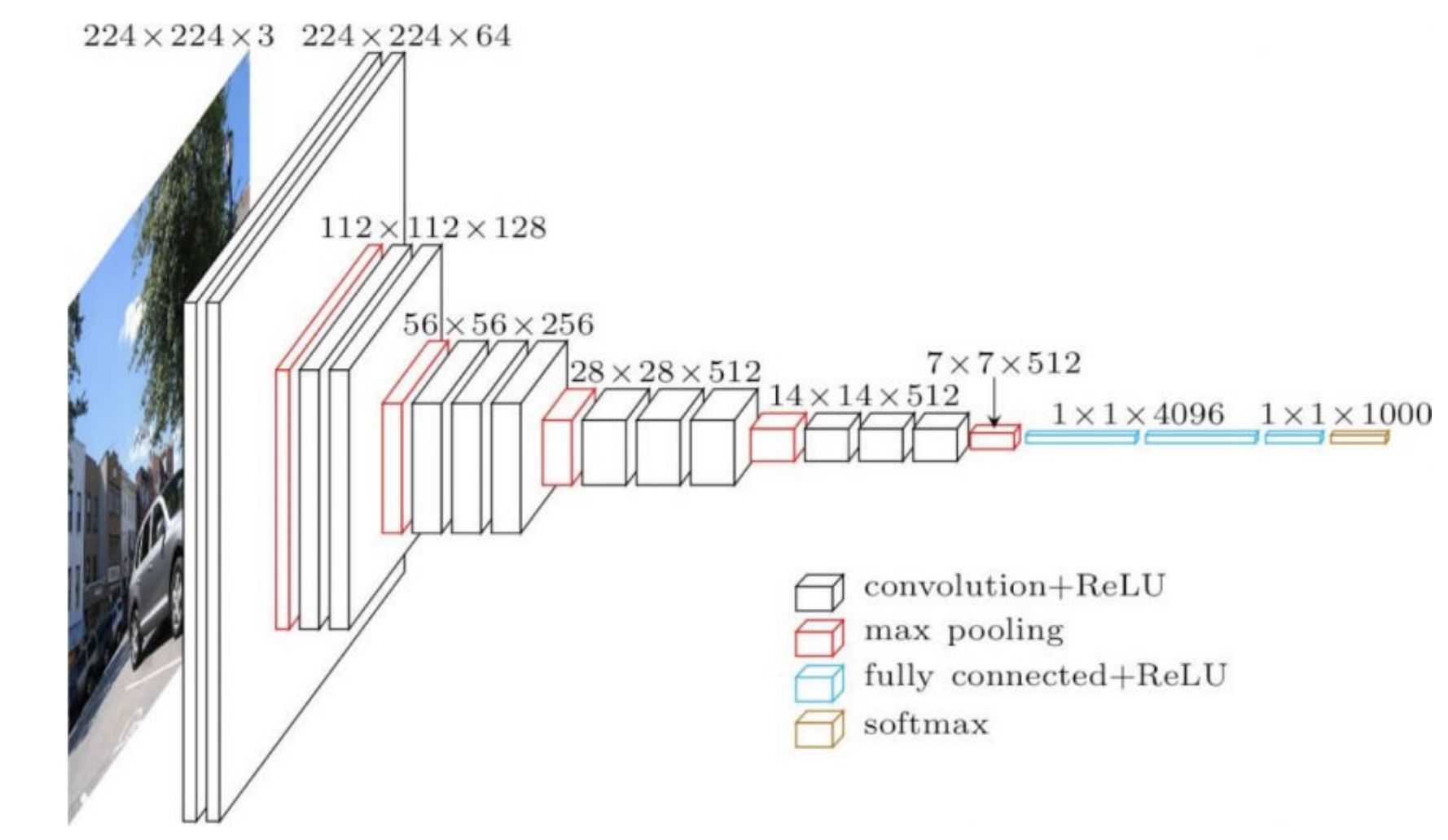
شكل 1: VGG16
RMSprop
الفكرة الأساسية لإنتشار جذر تربيع المتوسط (RMSprop, Root Mean Square Propagation) هي أن الإنحدار يتم تسويته باستخدام جذر تربيع المتوسط.
في المعادلة أدناه تربيع الإنحدار يدل على تربيع كل عنصر في المتجه منفرداً.
\[\begin{aligned} v_{t+1} &= {\alpha}v_t + (1 - \alpha) \nabla f_i(w_t)^2 \\ w_{t+1} &= w_t - \gamma \frac {\nabla f_i(w_t)}{ \sqrt{v_{t+1}} + \epsilon} \end{aligned}\]حيث $\gamma$ هي معدل التعلم العام و $\epsilon$ هي قيمة قريبة من $\epsilon$ الآلة (وتكون من مضاعفات $10^{-7}$ أو $10^{-8}$) – و تستعمل من أجل تجنب القسمة على صفر و $v_{t+1}$ هي عبارة عن مقدار العزم الثاني.
و نقوم بتحديث $v$ لتقدير القيمة المشوشة عن طريق المتوسط الأسي المتحرك (و هي طريقة أساسية لحساب متوسط كمية قد يمكن أن تتغير مع الزمن). نحن نحتاج أن نضع وزن كبير للقيم الجديدة ﻷنها تعطينا معلومات أكثر. واحدة من الطرق لفعل ذلك عن طريق تقليل وزن القيم القديمة أسياً. القيم القديمة جداً في حساب $v$ يتم تقليل وزنها في كل خطوة ثابتة $\alpha$ (تتراوح قيمتها بين صفر وواحد). هذا يؤدي إلى تثبيت القيم القديمة حتي تصير جزء غير معتبر في حساب المتوسط الأسي المتحرك.
تحافظ الطريقة الأصلية على متوسط أسي متحرك لعزم ثاني غير مركزي، لذلك لا نقوم بطرح قيمة المتوسط من المقدار هنا. يستخدم العزم الثاني لتسوية التدرج و هذا يعني أن كل عنصر في التدرج يتم قسمته على الجذر التربيعي للعزم الثاني. إذا كانت القيمة المتوقعة للتدرج صغيرة فأن هذه العملية مشابهة لقسمة التدرج على الانحراف المعياري.
استخدام قيمة صغيرة لـ $\epsilon$ في المقام لا يؤدي إلى الابتعاد عن النتيجة النهائية لأن عندما تكون $v$ صغيرة جدًا فإن الزخم يكون صغير جدًا.
ADAM
التقدير التَكَيُّفي للعزم (ADAM, Adaptive Moment Estimation) هي طريقة تتكون من RMSprop مع إضافة زخم (momentum). و هي طريقة شائع استخدامها. تحديث الزخم يتم تعدليه ليصبح متوسط أسي متحرك و لا نحتاج إلى تغيير معدل التعلم عندما نتعامل مع $\beta$. مثل RMSprop فأننا نأخذ جذر تربيع أسي متحرك لمربع الإنحدار.
\[\begin{aligned} m_{t+1} &= {\beta}m_t + (1 - \beta) \nabla f_i(w_t) \\ v_{t+1} &= {\alpha}v_t + (1 - \alpha) \nabla f_i(w_t)^2 \\ w_{t+1} &= w_t - \gamma \frac {m_{t}}{ \sqrt{v_{t+1}} + \epsilon} \end{aligned}\]حيث $m_{t+1}$ هي عبارة عن متوسط أسي متحرك.
تصحيح الإنحياز الذي يستخدم لجعل المتوسط الأسي المتحرك غير منحاز أثناء أول تكرارات غير موضح هنا.
جانب عملي
عند تدريب الشبكات العصبية فأن الإنحدار في SGD أحياناً يذهب في إتجاه خاطئ في بداية عملية التدريب و لكن RMSprop تقوم بتصحيح إتجاه الإنحدار. لكن RMSprop تعاني من التشويش مثل SGD فهي أيضاً قد تتردد حول قيمة محلية صغرى. مثل عندما نضيف زخم إلى SGD فإننا نحصل على نفس مقدار التحسين مع ADAM. ADAM تعتبر تقدير جيد و غير مشوش للحل و لذلك ADAM عموماً يوصى بها على RMSprop .
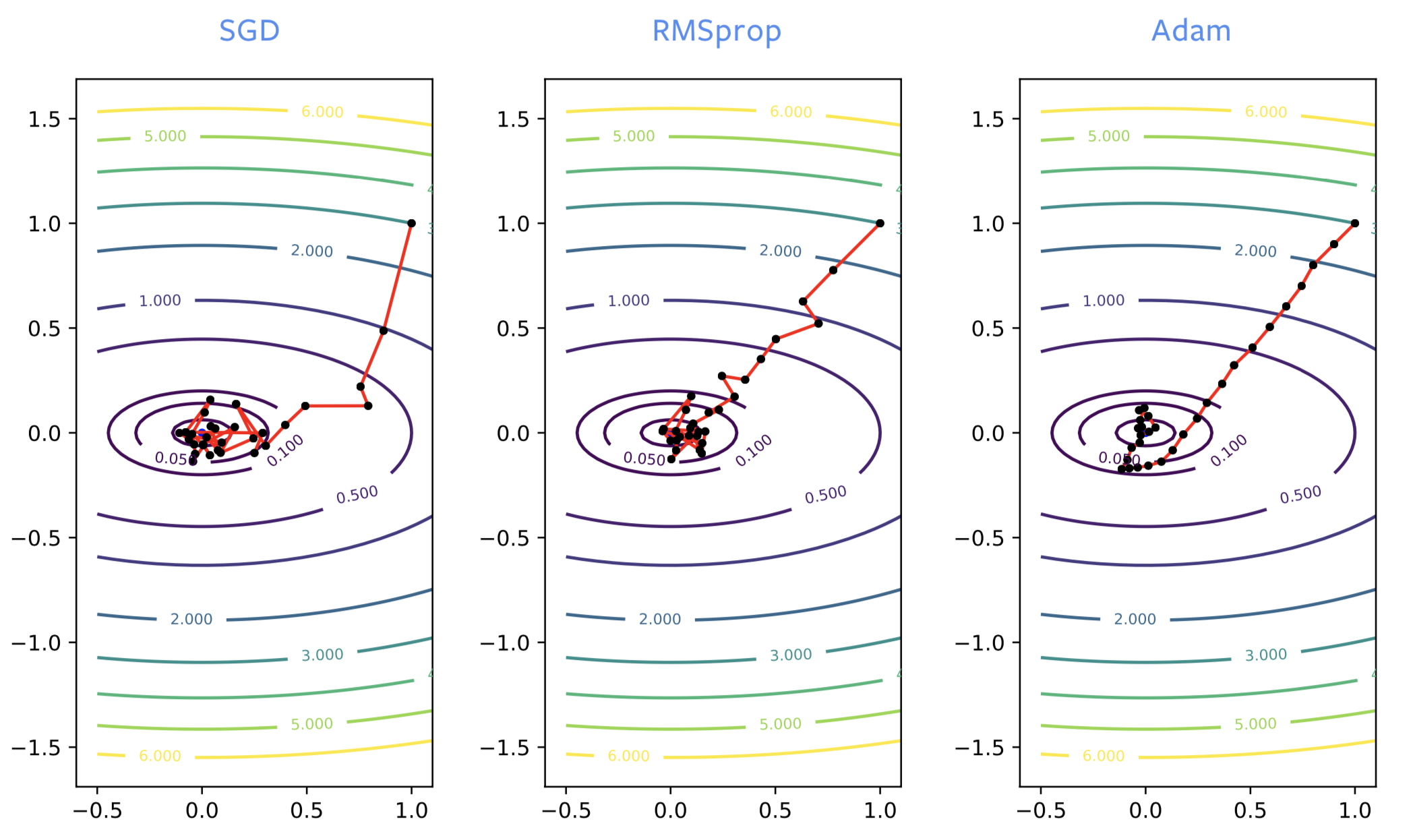
شكل 2: SGD *ضد* RMSprop *ضد* ADAM
ADAM ضرورية في تدريب بعض الشبكات مثل تلك التي تُستخدم لتكوين نماذج اللغات. من أجل تحسين الشبكات العصبية عادة ما يتم استخدام SGD مع الزخم أو ADAM. لكن الجانب النظري لـ ADAM غير مفهوم بصورة جيدة، كما لها عدة مساوىء منها:
- يمكن أن يثبت عن طريق إختبار بسيط أن الطريقة لا تتقارب لقيمة معينة
- من المعروف أن الطريقة تعطي أخطاء تعميم. إذا تم تدريب الشبكة العصبية لتعطي خسارة صفرية في البيانات التي تم تدريبها عليها فأنها لن تعطي خسارة صفرية على البيانات التي لم تراها الشبكة. أيضاً شائع - تحديداً في مشاكل الصور - أن تعطي أخطاء تعميم أسوء مقارنة بتلك الناتجة من SGD. الأسباب قد تتضمن مثلاً أنها تجد أقرب نقطة صغرى محلية أو أن هنالك تشويش أقل في ADAM أو من بنيتها.
- في ADAM نحتاج لإستخدام 3 مستودعات بينما في SGD نحتاج إلى إثنان فقط. هذا غير مؤثر إلا عندما ندرب نموذج حجمه يصل لعدد من القيقابايت و في هذه الحالة قد تكون الذاكرة غير كافية.
- نحتاج إلى ضبط معاملي زخم بدلاً عن واحد.
طبقات التسوية (Normalization layers)
بدلاً عن تطوير خوارزيميات التحسين، طبقات التسوية تطور بنية الشبكة نفسها. هي عبارة عن طبقات إضافية بين الطبقات الموجودة سابقاً في الشبكة. الهدف من وضعها هو تطوير جودة التحسين و التعميم.
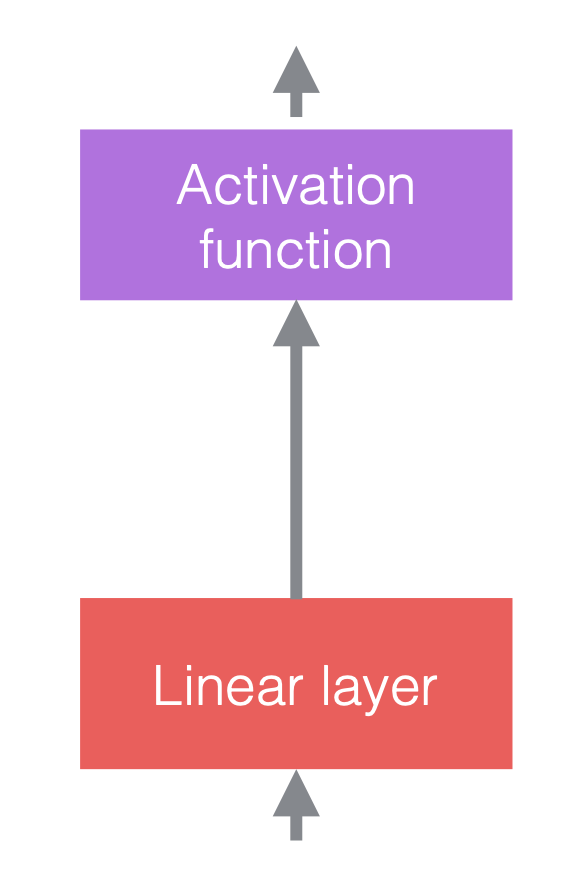
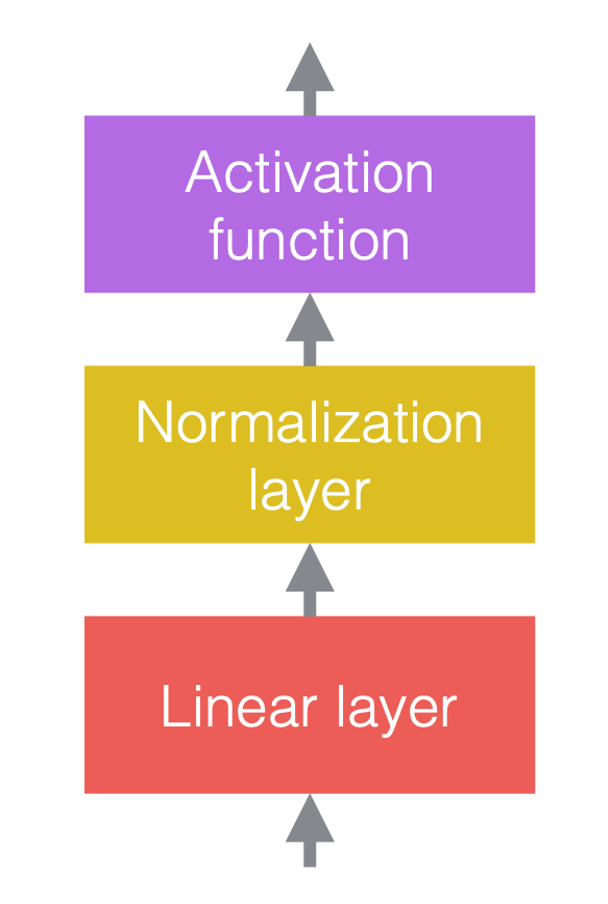
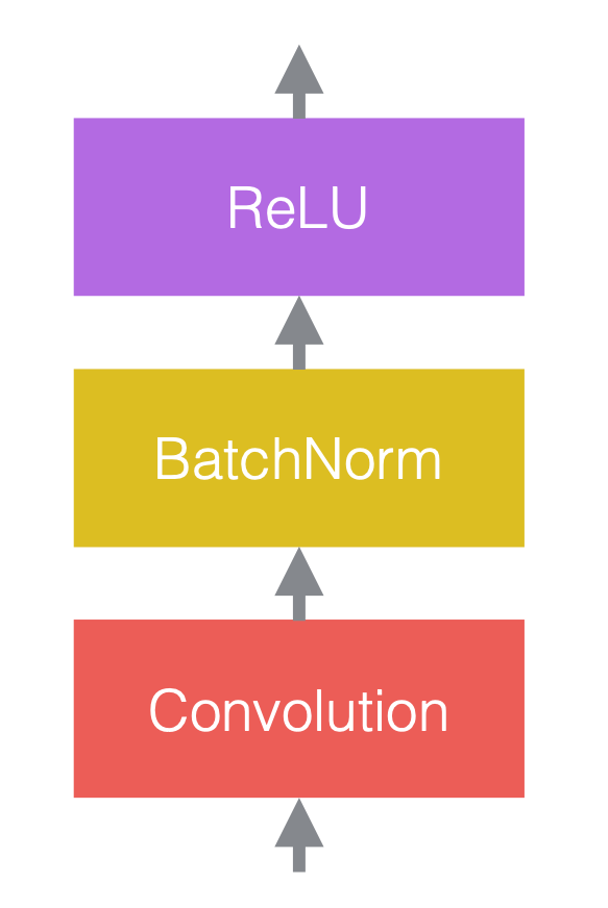
في الشبكات العصبية، ننتقل بين عمليات خطية وعمليات غير خطية. العمليات اللاخطية تعرف أيضاً بدوال التنشيط، مثلاً ReLU. يمكننا وضع طبقات التسوية قبل الطبقات الخطية أو بعد الطبقات اللاخطية. أكثر مكان شائع لوضعها هو ما بين الطبقات الخطية ودوال التنشيط كما موضح في الشكل أدناه.
 |
 |
 |
| (a) قبل إضافة طبقات التسوية | (b) بعد إضافة طبقات التسوية | (c) مثال باستخدام CNNs |
في شكل 3 (c) طبقة الإلتفاف هي الطبقة الخطية تتبعها طبقة تسوية ثم طبقة غير خطية ReLU.
لاحظ أن طبقات التسوية تؤثر على البيانات التي تمر من خلالها لكن لا تغير من قوة الشبكة مع تهيئة مناسبة للأوزان فأن شبكة بدون طبقات تسوية يمكن أن تعطي نفس المخرج لشبكة تستخدم طبقات تسوية.
عمليات التسوية
هذا هو التعبير العام للتسوية:
\[y = \frac{a}{\sigma}(x - \mu) + b\]حيث $x$ هو متجه الإدخال و $y$ هو متجه الإخراج و $\mu$ هي المقدر لمتوسط $x$و $\sigma$ هي المقدر للإنحراف المعياري لـ $x$ و $a$ هي معامل تكبير قابل للتعلم و $b$ هي معامل إنحياز قابل للتعلم.
بدون المعاملات القابلة للتعلم $a$ و $b$ فأن توزيع متجه الإخراج $y$ سوف يكون له متوسط ثابت 0 و إنحراف معياري 1. معامل التكبير $a$ و معامل الإنحياز $b$ يحافظان على قوة تمثيل الشبكة و يعني ذلك أن قيم المخرجات تكون في أي فترة معينة. لاحظ أن $a$ و $b$ لا يعكسان التسوية ﻷنهما عوامل قابلة للتعلم و أكثر ثباتاً من $\mu$ و $\sigma$.
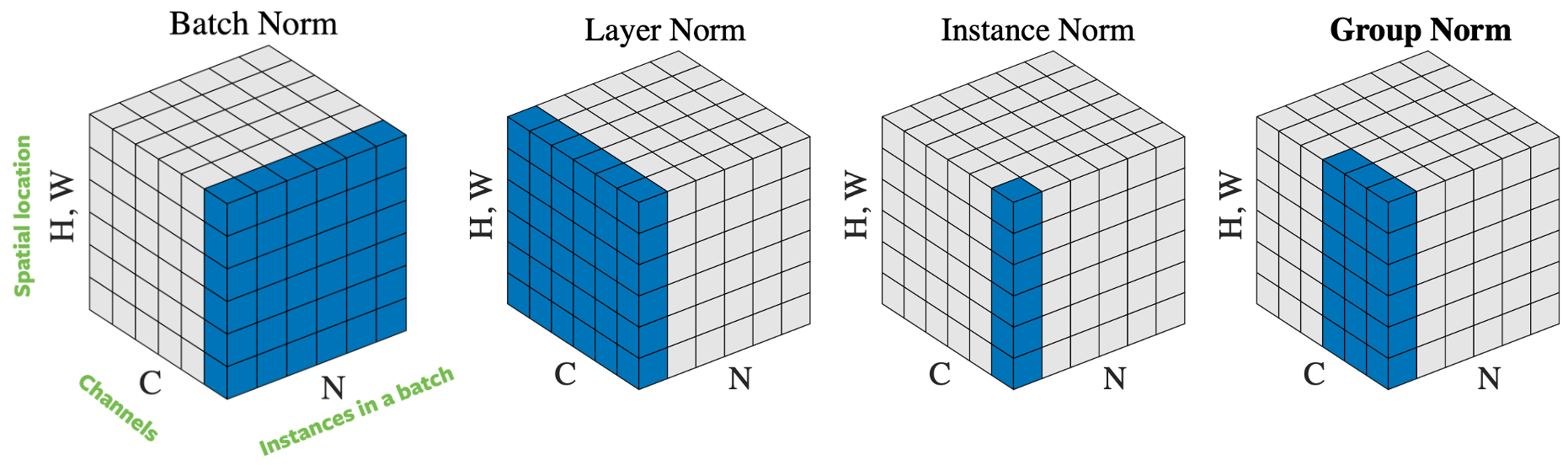
شكل 4: عمليات التسوية.
يوجد طرق عدة لتسوية متجه الإدخال إعتماداً على كيفية إختيار العينات التي يتم إستعمالها في التسوية. الشكل 4 يوضح 4 طرق مختلفة للتسوية. إذا كان لدينا حزمة صغيرة تتكون من $N$ صورة بإرتفاع $H$ و عرض $W$ و عدد قنوات $C$ فأن طرق التسوية هي:
- تسوية حزمة (Batch norm): التسوية يتم تطبيقها فقط على قناة واحدة من المدخل. هذه أول طريقة تم إقتراحها و أكثر الطرق شيوعاً. رجاءاً إقرأ هذا المقال How to Train Your ResNet 7: Batch Norm لتحصل على معلومات أكثر.
- تسوية طبقة (Layer norm): التسوية يتم تطبيقها على صورة واحدة عبر كل القنوات.
- تسوية مثال (Instance norm): التسوية يتم تطبيقها على صورة واحدة و قناة واحدة.
- تسوية مجموعة (Group norm): التسوية يتم تطبيقها على صورة واحدة و عدة قنوات. مثلاً القناة 0 إلى 9 هي مجموعة ثم القناة من 10 إلى 19 هي مجموعة أخرى و هكذا. عملياً فأن حجم المجموعة يكون غالباً 32. هذا الطريقة موصى بها من قبل Aaron Defazio لأن أدائها عملياً جيد و لا تتعارض مع SGD.
عملياً فأن تسوية الحزمة و تسوية المجموعة تعمل جيداً في مشاكل رؤية الحاسوب بينما تسوية الطبقة و المثال تستخدم بكثرة في مشاكل معالجة اللغات.
لماذا تساعد التسوية في تحسين التدريب؟
رغماً أن التسوية تعمل جيداً عملياً إلا أن الأسباب وراء فعاليتها غير متفق عليها. تم إقتراح التسوية لتقليل الإزاحة المتغيرة داخلياً “internal covariate shift” لكن بعض الباحثين أثبتوا أن هذا الأفتراض خاطىء في التجارب. بالإضافة التسوية تتكون من مجموعة العوامل التالية:
- الشبكة التي تحتوي على طبقات تسوية تحسينها أسهل و هذا يسمح باستعمال معدلات تعلم عالية. التسوية لديها تأثير تحسيني يسرع من عملية تدريب الشبكة العصبية.
- تقديرات المتوسط و الإنحراف تكون مشوشة بسبب عشوائية العينات في الحزمة المعينة. هذه العشوائية الزائدة تؤدي إلى تعميمات أفضل في بعض الحالات. التسوية لها تأثير تنظيمي (regularization).
- التسوية تقلل من حساسية تهيأة الأوزان.
كنتيجة التسوية تجعلك أقل حذراً فيمكنك تكوين شبكة من أي أجزاء و تحصل على نتائج جيدة بدون إعتبار سوء تنفيذك.
إعتبارات عملية
من المهم أن يحسب الإنتشار الخلفي من خلال حساب المتوسط و الإنحراف المعياري كما يتم في تطبيق التسوية و إلا فأن تدريب الشبكة سوف يتباعد. حساب الإنتشار الخلفي صعب و معرض للأخطاء لكن إطار PyTorch يستطيع أن يحسبه تلقائياً و هذا مفيد جداً. طبقتين تسوية من نوعين مختلفين في PyTorch موضحات أدناه:
torch.nn.BatchNorm2d(num_features, ...)
torch.nn.GroupNorm(num_groups, num_channels, ...)
تسوية الحزمة هي أول طريقة تم تطويرها و أكثر الطرق شيوعاً. لكن Aaron Defazio يوصي باستخدام تسوية المجموعة. تسوية المجموعة أكثر ثباتاً و نظرياً أبسط و غالباً تعمل بصورة جيدة. استعمال حجم مجموعة مساو ل 32 إختيار جيد.
لاحظ أنه بالنسبة لتسوية حزمة و تسوية مثال، يتم إصلاح المتوسط / الانحراف المعياري بعد التدريب ، بدلاً من إعادة حسابه في كل مرة يتم فيها تقييم الشبكة، لأن هناك حاجة إلى عينات تدريب متعددة لإجراء التسوية. هذا ليس ضروريًا لتسوية مجموعة أو طبقة، نظرًا لأن تسويتها يتجاوز عينة تدريب واحدة فقط.
موت التحسينات
أحياناً ندخل في مجال لا نعلم عنه شيئاً و نطور الطرق المستعملة فيه. كمثال استخدام الشبكات العصبية العميقة في مجال تصوير الرنين المغنيطيسي (MRI) في تسريع إعادة تكوين صور الMRI.

شكل 5: أحياناً، إنها تعمل بالفعل!
إعادة تكوين صور الرنين المغنطيسي (MRI Reconstruction)
في مشكلة إعادة تكوين صور الـ MRI تؤخذ البيانات المجردة من جهاز الرنين المغنطيسي و يتم إعادة تكوين الصورة باستخدام خوارزمية. أجهزة الـ MRI تلتقط البيانات في مجال فورير ثنائي الأبعاد، صف واحد أو عمود واحد في المرة الواحدة (كل أجزاء من الثانية). هذا المدخل يتكون من تردد و قناة طور و القيمة تمثل مقدار دالة جيبية لديها نفس التردد و الطور. ببساطة يمكن أن نعتبرها صورة قيمها أعداد مركبة و تحتوي على قناة حقيقية و قناة تخيلية. إذا طبقنا تحويل فورير العكسي على هذا المدخل - عن طريق جمع كل الموجات الجيبية (sine waves) موزونة بقيمها - فأننا سنحصل على الصورة الأصلية.
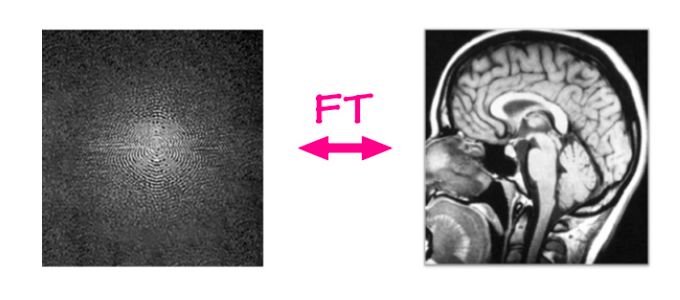
شكل 6: إعادة تكوين MRI
يوجد تحويل خطي من مجال فورير إلى مجال الصورة و كفاءته جيدة و يأخذ أجزاء من الثانية بغض النظر عن كبر حجم الصورة. لكن السؤال هل يمكن أن نحصل على سرعة أكبر.
MRI المسرعة
المشكلة الجديدة التي تحتاج إلى أن حل هي تسريع الـ MRI و نعني بالتسريع أن نجعل عملية إعادة تكوين الـ MRI أسرع. و نريد أن نحافظ على جودة الصورة. واحدة من الطرق ومن الطرق الأكثر نجاحاً هي أن لا نلتقط جميع الأعمدة من ماسح الـ MRI. يمكننا أن نتجاهل بعض الأعمدة عشوائياً لكن عملياً إلتقاط الأعمدة الموجودة في الوسط أكثر فائدة ﻷنها تحتوي على معلومات كثيرة و يمكن أن نختار عشوائياً خارج المنطقة الوسطى. تكون المشكلة أنه لا يمكننا إستعمال التحويل الخطي لإعادة تكوين الصورة مرة أخرى. الصورة الموجودة على أقصى اليمين في شكل 7 توضح مخرج التحويل الخطي المطبق على فضاء فورير. من الواضح أن هذه الطريقة لا تعطينا مخرجات مفيدة جداً و هنالك مجال لتحسينها.

شكل 7 التحويل الخطي في فراغ فورير
Compressed sensing (الاستشعار المضغوط)
واحدة من أكبر الاكتشافات في مجال الرياضيات النظرية لوقت طويل هي الاستشعار المضغوط. ورقة علمية بواسطة Candes et al. توضح نظرياً أنه يمكن الحصول صورة مثالية معاد تكوينها من مجال فورير. بصورة أخرى فأن الموجة التي نحاول أن نعيد تكوينها تكون منتشرة أو بنيتها منتشرة لكن يمكننا أن نعيد تكوينها بصورة مثالية من عدة قياسات قليلة. لكن توجد متطلبات عملية لكي تعمل هذه الطريقة – لا نحتاج لأخذ عينات عشوائياً لكن نحتاج لأخذ عينات بصورة غير منتظمة – لكن عملياً الناس يأخذون عينات عشوائية. بالأضافة أخذ عينة من عمود كامل أو نص عمود يحتاج إلى زمن لذلك عملياً نأخذ عينات من أعمدة كاملة.
و نحتاج إلى شرط أخر و هو أن وجود الانتشار (sparsity) في الصورة و نعني بالإنتشار أن تكون في الصورة بيكسلات صفرية أو سوداء كثيرة. المدخل يمكن أن نمثله إنتشارياً عن طريق مفكوك الطول الموجي لكن حتى هذا المفكوك يعطينا إنتشاراً مقرباً و ليس صورة منتشرة بالتحديد. لذلك هذه الطريقة تعطينا صورة جيدة جداً كما في الشكل 8. لكن إذا كان المدخل منتشر جداً في مجال الطول الموجي فإننا سنحصل على صورة مثالية.
\[\hat{x} = \arg\min_x \frac{1}{2} \Vert M (\mathcal{F}(x)) - y \Vert^2 + \lambda TV(x)\]حيث $M$ هي دالة غطائية تُصفِّر كل عنصر غير مختار و $\mathcal{F}$ هو عبارة عن تحويل فورير و $y$ هي البيانات المشاهدة في مجال فورير و $\lambda$ هي معامل قوة التنظيم و $V$ هي دالة التنظيم.
مشكلة التحسين يجب أن تُحل لكل خطوة زمن أو كل قطعة في مسح الـ MRI و أحياناً تأخذ زمناً أطول من المسح نفسه. و هذا سبب آخر للبحث عن شيء أفضل.
ماالذي بحاجة للتحسين؟
بدلاً عن حل مشكلة التحسين الصغيرة هذه في كل خطوة زمن لماذا لا نستعمل شبكة عصبية كبيرة لإنتاج الحل المطلوب؟ أملنا هو أن ندرب شبكة عصبية بتعقيد مناسب من أجل حل مشكلة التحسين في خطوة واحدة و إنتاج مخرج جيد مثل الذي نحصل عليه من حل مشكلة التحسين في كل خطوة زمنية.
\[\hat{x} = B(y)\]حيث $B$ هو نموذج الشبكة العصبية العميق و $y$ هي بيانات مجال فورير التي نراقبها.
قبل 15 سنة، كانت هذه الطريقة صعبة، لكن اﻵن أصبح تنفيذها أكثر سهولةً. شكل 9 يوضح نتائج طريقة التعلم العميق و نرى أن المخرج أفضل من مخرج طريقة الإستشعار المضغوط و يشبه جداً الصورة المأخوذة من مسح عادي.
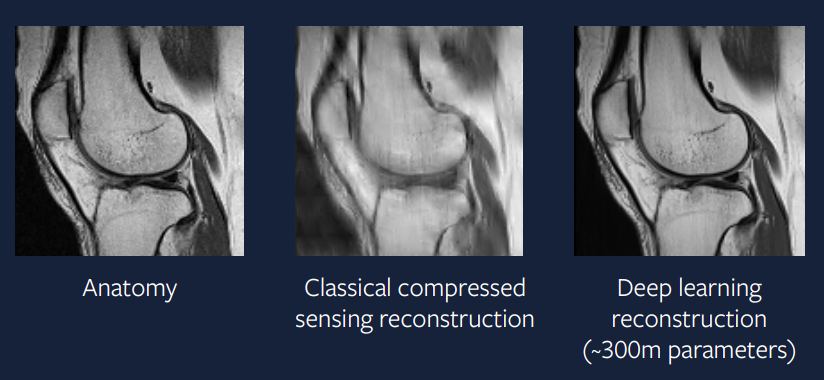
شكل 9: طريقة التعلم العميق
النموذج المستخدم لإعادة تكوين الصور يستخدم محسن ADAM و طبقات تسوية مجموعة و U-Net CNN. هذه الطريقة قريبة جداً من التطبيقات العملية و نأمل أن نرى مسح MRI المسرع قريباً يستخدم في العيادات في السنوات القليلة القادمة.
📝 Guido Petri, Haoyue Ping, Chinmay Singhal, Divya Juneja
Mohammed Almakki
24 Feb 2020