تقنيات التحسين الجزء الاول
🎙️ Aaron Defazioالإنحدارالتدريجي
نبتدأ دراستنا لطرق التحسين بأبسط الاساليب الممكنة طريقة الكل شيء الانحدار التدريحي مسألة:
\[\min_w f(w)\]الطريقة التكرارية:
\[w_{k+1} = w_k - \gamma_k \nabla f(w_k)\]بحيث أن
- $w_{k+1}$ > هي القيمة المحدثة بعدد تكرار $k$-th
- $w_k$ > هي القيمة الأبتدائية قبل التكرار $k$-th
- $\gamma_k$ > مقياس الخطوة
- $\nabla f(w_k)$ > التدريج الخاض بالمتغير $f$
مع الوضع في الحسبان أن الدالة $f$ هي دالة مستمرة وقابلة للأشتقاق هدفنا هو أن نجد اكثر نقطة منخفضة (الوادي) لدالة التحسين. بغض النظر عن اتجاه هذا الوادي أي أن الاتجاه غير معلوم. نحن فقط سنرى ونبحث بشكل محلي ولذلك الأتجاه السلبي التدريجي يعتبر أفضل معلومة لدينا. اتخاذ خطوة صغيرة إلى ذلك الأتجاه سيقربنا للحد الادنى. ما أن نأخذ خطوة صغيرة سنعيد مره اخرى تحديد التدريج الجديد ومره أخرى سنتحرك لذاك الأتجاه بكميات وخطوات صغيرة حتى نصل للوادي. وبشكل عام ما يفعله الانحدار التدريجي هو إتباع أتجاه شديد الانحدار (تدريج سلبي)
المدخل $\gamma$ في المعادلة التحديثية التكرارية يسمى مقياس الخطوة. بشكل عام نحن لا نعرف القيمة المثالية لمقياس الخطوة ولذلك سنضطر تجربة قيم مختلفة. المعيار القياسي سيكون تجربة مجموعة من القيم على ميزان للأداء ونختار أفضل قيمة بناء على الميزان. هنالك سناريوهات مختلفة قد تحدثز الصورة بالأعلى تصف هذه السناريوهات بالنسبة 1D quadratic.إذا معدل التعلم منخفض للغاية إذن سنضطر لخلق تقدم ثابت للوصول إلى الحد الأدنى.ولكن هذه الخطوة ستأخذ وقت اطول من الوقت المثالي. صعب جدا (وشبه مستحيل ) أن نحصل على مقياس خطوة يصلنا بشكل مباشر للحد الأدنى. ما سنريده بشكل مثالي هو أن نحصل على مقياس خطوة اكبر بقليل من القياس المثالي. هذا ما سعطينا اسرع تقارب (convergence). ولكن إذا استعملنا معدل تعلم كبير التكرار سيصبح أبعد وأبعد من الحد الأدنى وسنحصل على تباعد (divergence). نريد أن نستعمل معدل تعلم قليل البعد (less diverging).
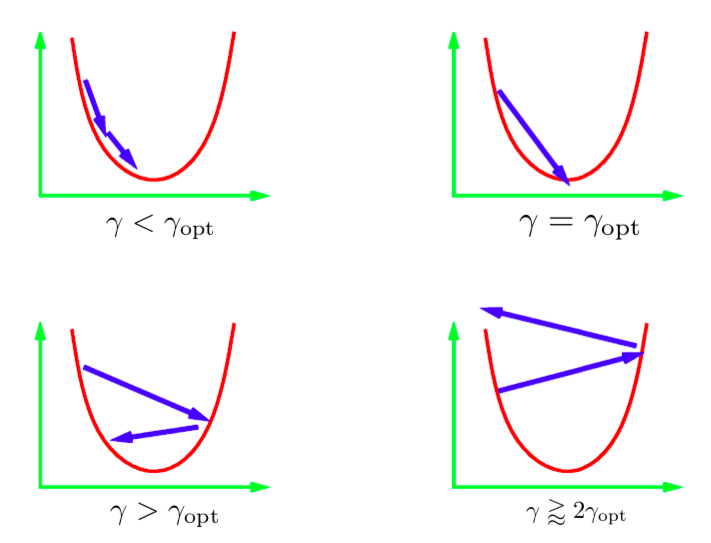
الشكل 1: مقياس خطوات 1D Quadratic
صعود تدريجي عشوائي SGA
في الصعود التدريجي العشوائي سنبدل اتجاه التدريج بمعدل عشوائي. لخلية عصبونية معدل العشوائية يعني تدرج الخسارة لنقطة بيانية.
$f_i$ > ستمثل الخسارة في الشبكة للنموذج $i$-th \(f_i = l(x_i, y_i, w)\)
الدالة التي نريد خفضها او خفض قيمته هي $f$, الخسارة الكلية لجميع النماذج \(f = \frac{1}{n}\sum_i^n f_i\)
في النزول التدريجي العشوائي (SGD) سنحدث الاوزان تناسبا مع التدرج على $f_i$ (بالنسبة إلى التدرج على معدل الخسارة الكلي $f$) \(\begin{aligned} w_{k+1} &= w_k - \gamma_k \nabla f_i(w_k) & \quad\text{(i chosen uniformly at random)} \end{aligned}\)
إذا تم اختيار $i$ بشكل عشوائي إذن $f_i$ تعتبر مزعجة (noisy) ولكنها مقدار غير متحيز, والذي سيكتب بشكل رياضي بصيغة: \(\mathbb{E}[\nabla f_i(w_k)] = \nabla f(w_k)\)
وكأستنتاج, الخطوة المتوقعة $k$-th في النزول التدريجي العشوائي (SGD) هي نفس خطوة $k$-th في الانحدار التدريجي: \(\mathbb{E}[w_{k+1}] = w_k - \gamma_k \mathbb{E}[\nabla f_i(w_k)] = w_k - \gamma_k \nabla f(w_k)\)
وبهكذا نستطيع القول بأن أي تحديث للـSGD هو بنفس تحديث الـfull-batch من ناحية التوقع. ولكن الـ(SGD)ليست فقط للنزول التدريجي السريع مع ازعاج. ومع كونه سريع الـ(SGD) يستطبع ايضا جلب نتائج أفضل من نتائج النزول التدريجي للـfull-batch. الازعاج في الـ(SGD) يستطيع ايضا مساعدتنا لتجنب سطحية القيمة الصغرى المحلية وايجاد قيمة صغرى افضل (واعمق) هذه الظاهرة تسمى تليين (Annealing)
الشكل 2: التليين مع SGD
بشكل مختصر فوائد النزول التدريجي العشوائي هي:
- هنالك الكثير من المعلومات المتكررة في جميع النماذج. الـ(SGD) يمنع الكثير من تلك العمليات المكررة.
- في المراحل الابتدائية الازعاج يعتبر بكميات قليلة مقارنة بالمعلومات في التدرج. وهكذا خطوة الـ(SGD) جيدة مثل خطوة الـGD ولكن بشكل افتراضي
- التليين - الازعاج في تحديث SGD يستطيع أن يمنع التقارب لقيمة صغرى محلية سيئة (سطحية)
- النزول التدريجي العشوائي تكلفة تشغيله تعتبر منخفضة (لأنك لن تتجاوز جميع النقاط البيانات).
(Mini-batching) التحزيم الصغير
في التحزيم الصغير سنضع بعين الاعتبار الخسارة على العديد من نماذج المختارة بشكل عشوائي بدلا من حسابها على نموذج واحد فقط. وهذا سيقلل الازعاج في خطوة التحديث
\[w_{k+1} = w_k - \gamma_k \frac{1}{|B_i|} \sum_{j \in B_i}\nabla f_j(w_k)\]نحن غالبا نستطيع تحسين استخدام الـhardware الخاص بنا بواسطة استخدام حزم صغيرة بدلا من نموذج وحيدة. مثلا وحدات معالجة الرسومات (GPUs)تعتبر مستخدمة بشكل ضعيف عندما نستخدم نموذج تدريبي وحيد. تقنيات الشبكة التدريبية المنتشرة تفصل كمية كبيرة من الحزم الصغيرة بين مجموعة من الآت ومن ثم تجمع التدريج الناتج. مؤخرا فيسبوك دربت شبكة على بيانات الـImageNet بغضون ساعة باستخدام التدريب المنتشر.
مهم نتذكر أن الالانحدار التدريجي لا يجب أن لا يستخدم حزم بحجم كامل. في حال اردت أن تدرب بحزم ذات حجم كامل يجب عليك أن تستخدم تقنية تحسين تسمى LBFGS. كل من PyTorch و SciPy توفران تنفيذ لهذه التقنية.
قوة الدفع
في قوة الدفع نمتلك متكررين اثنين بدلا من متكرر واحد وهما $p$ و $w$. التحديثات كالآتي: \(\begin{aligned} p_{k+1} &= \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} &= w_k - \gamma_kp_{k+1} \\ \end{aligned}\)
يسمى الـ$p$ بقوة الدفع لـSGD في كل تحديث خاص للخطوة نضيف تدريج عشوائي للقيمة القديمة الخاصة بقوة الدفع وبعد اخمادها بعامل $\beta$ (قيمة بين 1 و 0). نستطيع التفكير بـ$p$ وكأنها متوسط للتدريجات. واخيرا نحرك $w$ بأتجاه قوة الدفعة الجديدة $p$ شكل بديل: Stochastic Heavy Ball Method
\[\begin{aligned} w_{k+1} &= w_k - \gamma_k\nabla f_i(w_k) + \beta_k(w_k - w_{k-1}) & 0 \leq \beta < 1 \end{aligned}\]هذا الشكل يساوي بشكل رياضي الشكل السابق. هنا الخطوة التالية هي مزيج من اتجاه الخطوة السابقة ($w_k - w_{k-1}$) و التدريج السلبي الجديد.
بديهيات
قوة دفع SGD مشابهه لمبدأ قوة الدفع في الفيزياء. عملية التحسين تمثل كرة ثقيلة تتدحرج من اسفل التل. قوة الدفع تجعل الكرة مستمرة بالحركة بنفس الاتجاه. يمكن التفكير بالتدريج وكأنه القوة المعاكسة التي تدفع الكرة بالأتجاه الاخر.

الشكل 3: تأثير قوة الدفع
المصدر: distill.pub
بدلا من احداث تغييرات كبيرة بأتجاه السفر (مثل ما تمثل الصورة التي على اليسار), قوة الدفع تتخذ تغييرات بسيطة. قوة الدفع تُخمد التذبذبات التي تعتبر دارجة بما أننا سنستخدم SGD فقط المعامل $\beta$ يسمى بعامل الاخماد, ويجب أن يكون أعلى من الصفر لأن إذا كان يساوي الصفر فسيكون انحدار تدريجي وايضا يجب أن يكون اقل من 1 وإلا سترتفع قيمته بشكل مبالغ, القيم الصغيرة للـ$\beta$ تنتج تغير سريع للأتجاه بينما القيم الكبيرة ستأخذ منعطفات اكثر.
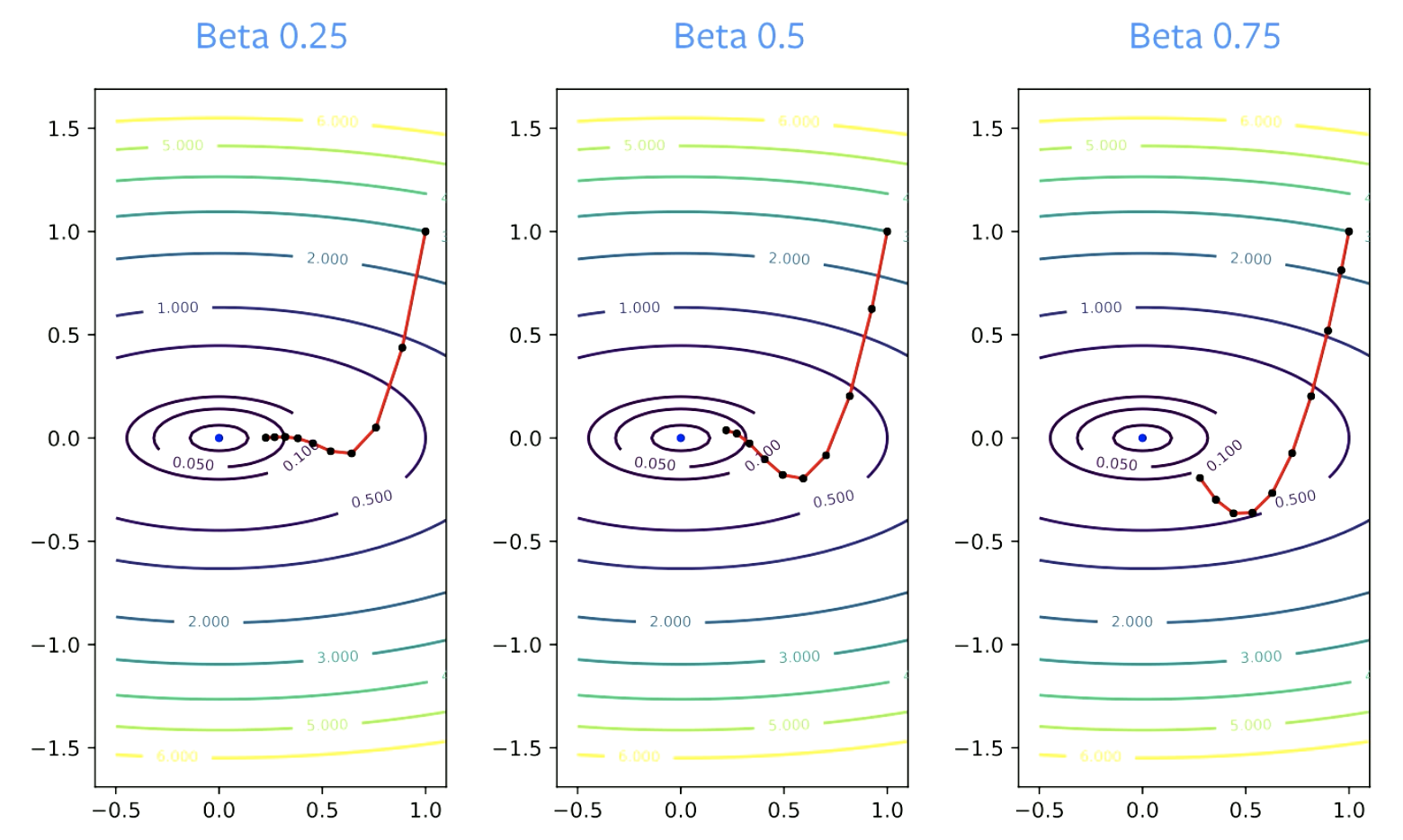
الشكل 4: تأثير بيتا بالتقارب
إرشادات عملية
قوة الدفع يجب أن تستعمل مع النزول التدريجي العشوائي $\beta$ = 0.9 او 0.99 دائما تعمل. عامل مقياس الخطوة غالبا يحتاج أن يكون منخفض عندما يكون عامل قوة الدفع مرتفع لكي يحافظ على التقارب. إذا تغيرت $\beta$ من 0.9 إلى 0.99 مهدل التعلم يجب أن ينخفض بعامل 10
لماذا تعمل قوة الدفع؟
التسارع
مايلي تحديث لقوانين قوة دفع نستروف. \(p_{k+1} = \hat{\beta_k}p_k + \nabla f_i(w_k) \\ w_{k+1} = w_k - \gamma_k(\nabla f_i(w_k) +\hat{\beta_k}p_{k+1})\)
ناس كثر يقولون بأن قوة الدفع الطبيعية هي ايضا طريقة تسارع ولكن بالواقع هي متسارعة فقط للـquadratics التسارع لا يعمل جيدا مع SGD لان الـSGD تملك ازعاج والتسارع لا يعمل جيدا مع الازعاج ولهذا بعض اجزاء التسارع تكون حاضرة مع قوة دفع SGD ولكنها لوحدها لا لا تعتبر مثال جيد لتقنية الاداء العالي.
مهدأ الازعاج
سبب عمل قوة الدفع هو هو مهدأ الازعاج.
قوة الدفع توسط التدريجات وهي ايضا متوسط التدريجات التي نستخدمها لكل تحديث خطوة.
بشكل نظري لكي تعمل SGD يجب علينا أن نستغل تحديثات الخطوات. \(\bar w_k = \frac{1}{K} \sum_{k=1}^K w_k\)
الشيء العظيم بخصوص SGD ذات قوة الدفع هو أن هذا الالتوسط averaging لم يعد ضروريا, قوة الدفع تضيف مهدأ لعملية التحسين مما يجعل كل تحديث تقريب جيد للحل. مع SGD ستوجب عليك توسيط مجموعة تحديثات واتخاذ خطوة لذاك الأتجاه كل من التسارع و مهدأ الازعاج تساهم لأداء مرتفع لقوة الدفع
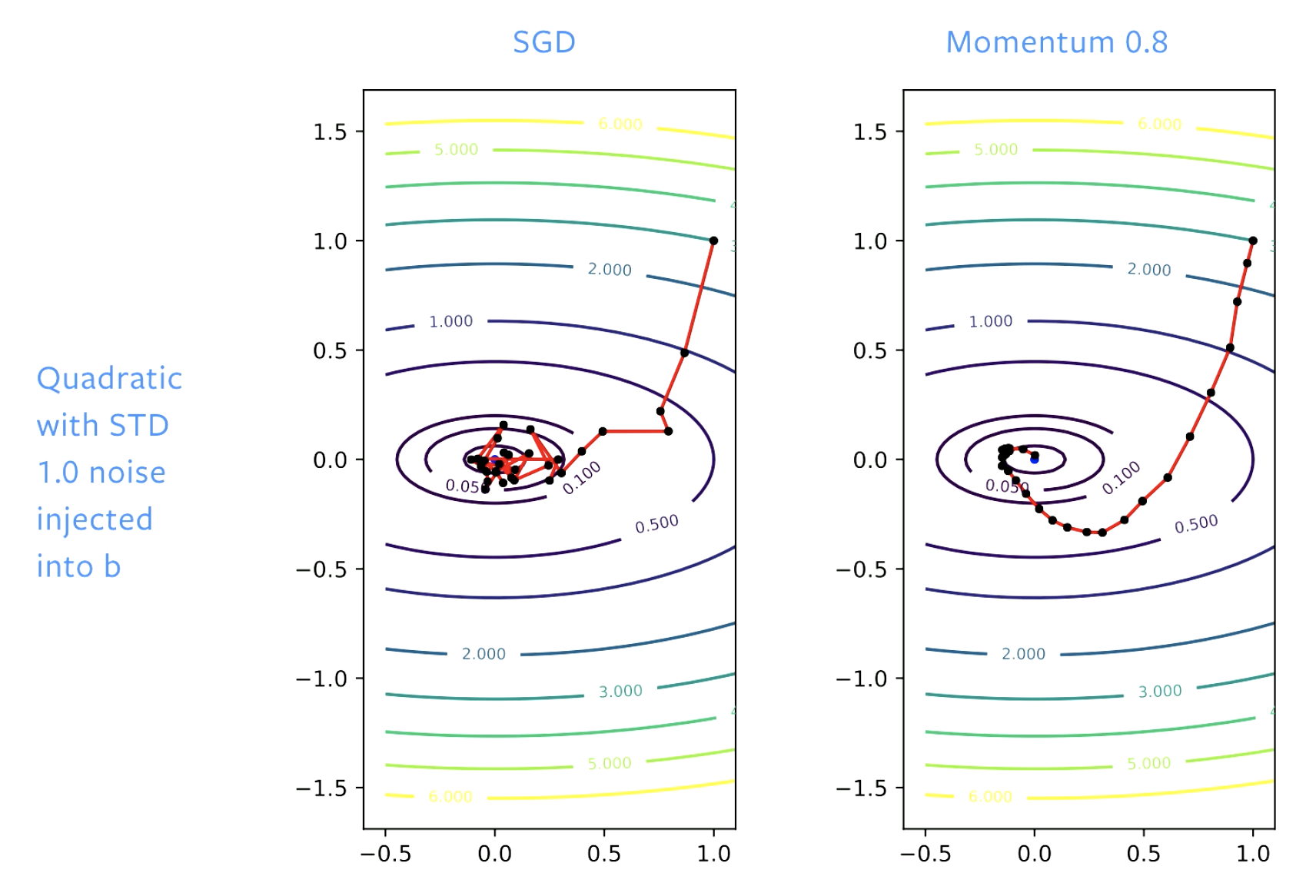
الشكل 5: SGD *مقابل* قوة الدفع
مع SGD نتقدم للحل الابتدائي ولكن عندما نصل إلى قاع الوادي نقفز بأرجاء هذه الارض إذا فقط عدلنا معدل التعلم ستقفز بالارجاء ولكن بشكل بطيء مع قوة الدفع نحن نهدأ الخطوات لكي لا يكون هناك قفز بالارجاء
📝 Vaibhav Gupta, Himani Shah, Gowri Addepalli, Lakshmi Addepalli
Wejdan AlOtaibi
24 Feb 2020