خصائص الإشارات الطبيعية

خصائص الإشارات الطبيعية

يمكن التفكير في مختلف أنواع الاشارات على أنها متجهات. على سبيل المثال الإشارة الصوتية يمكن اعتبارها متجه أحادي البعد $\boldsymbol{x} = [x_1, x_2, \cdots, x_T]$ حيث كل قيمة $x_t$ تمثل اتساع الموجة الصوتية في الزمن $t$. ولكي تستطيع أن تفهم ما ينطق به شخص ما، تقوم قَوْقَعَةُ الأُذُن اولا بتحويل ضغط الهواء الناتج عن الموجات الصوتية إلى اشارات وبعد ذلك يقوم العقل باستخدام نموذج لغوي إلى تحويل تلك الموجات إلى لغة، أي عليه اختيار الكلام الأقرب احتمالاً من الموجة المسموعة. بالنسبة للموسيقى، تكون الإشارة مجسمة تحتوي على قناتين أو أكثر لتوهم أن الصوت يأتي من اتجاهات متعددة. و على الرغم من أنها تحتوي على قناتين، إلا أنها لا تزال إشارة 1D لأن الوقت هو المتغير الوحيد.

الصورة هي إشارة ثنائية الأبعاد لأن المعلومات مصورة مكانيًا. لاحظ أن كل نقطة يمكن أن تكون متجهًا في حد ذاته. هذا يعني أنه إذا كان لدينا قنوات $d$ في صورة ما، فإن كل نقطة مكانية في الصورة هي متجه للأبعاد $d$. تحتوي الصورة الملونة على مستويات RGB، مما يعني أن $d = 3$. لأي نقطة $x_{i,j}$، هذا يتوافق مع شدة الألوان الأحمر والأخضر والأزرق على التوالي.

يمكننا حتى تمثيل اللغة بالمنطق أعلاه. تتوافق كل كلمة مع متجه واحد نشط بمعنى وجود واحد في الموضع الذي يظهر في مفرداتنا وأصفارنا في كل مكان آخر. هذا يعني أن كل كلمة هي متجه لحجم المفردات.

تتبع إشارات البيانات الطبيعية هذه الخصائص:

1. الثبات: تتكرر أشكال معينة خلال الإشارة. في الإشارات الصوتية، نلاحظ نفس النوع من الأنماط مرارًا وتكرارًا عبر المجال الزمني. اما في الصور، هذا يعني أنه يمكننا توقع تكرار أنماط بصرية مماثلة عبر الأبعاد.

2. الموقع المحلي: النقاط القريبة أكثر ارتباطًا من النقاط البعيدة. بالنسبة للإشارة 1D، هذا يعني أننا إذا لاحظنا ذروة عند نقطة ما $t_i$، فإننا نتوقع أن يكون للنقاط في نافذة صغيرة حول $t_i$ قيم مماثلة لـ $t_i$ ولكن لنقطة $t_j$ بعيدة عن $t_i$، $x_{t_i}$ له تأثير أقل على $x_{t_j}$. بشكل أكثر تحديدا، يكون الالتفاف بين الإشارة ونظيرتها المقلوبة ذروته عندما تتداخل الإشارة تمامًا مع نسختها المقلوبة. الالتفاف بين إشارتين 1D (الارتباط المتبادل) ليس سوى حاصل الضرب النقطي الخاص بهما وهو مقياس لمدى تشابه أو قرب المتجهين. وبالتالي، يتم احتواء المعلومات في أجزاء وأجزاء محددة من الإشارة. بالنسبة للصور، هذا يعني أن الارتباط بين نقطتين في صورة ما يقل كلما ابتعدنا عن النقاط. إذا كان $x_{0,0}$ باللون الأزرق، فإن احتمال أن يكون البكسل التالي ($x_{1,0},x_{0,1}$) أزرق أيضًا يكون مرتفعًا جدًا ولكن مع انتقالك إلى الطرف المقابل للصورة ($x_{-1,-1}$) ، قيمة هذا البكسل مستقلة عن قيمة البكسل عند $x_{0,0}$ .

3. التكوين: كل شيء في الطبيعة يتكون من أجزاء تتكون من أجزاء فرعية وما إلى ذلك. على سبيل المثال، تشكل الحروف سلاسل تشكل الكلمات، والتي تشكل الجمل بشكل أكبر. يمكن دمج الجمل لتشكيل المستندات. تسمح التركيبة للعالم بأن يكون قابلاً للتفسير.

إذا أظهرت بياناتنا الثبات، والمكان، والتكوين، فيمكننا استغلالها مع الشبكات التي تستخدم التباين ومشاركة الوزن وتكديس الطبقات.

استغلال خصائص الإشارات الطبيعية لبناء الثبات والتوازن

المحلية $\Leftarrow$ التناثر.

يوضح الشكل 1 شبكة متصلة بالكامل من 5 طبقات. يمثل كل سهم وزنًا يتم ضربه في المدخلات. كما نرى، هذه الشبكة مكلفة للغاية من الناحية الحسابية.

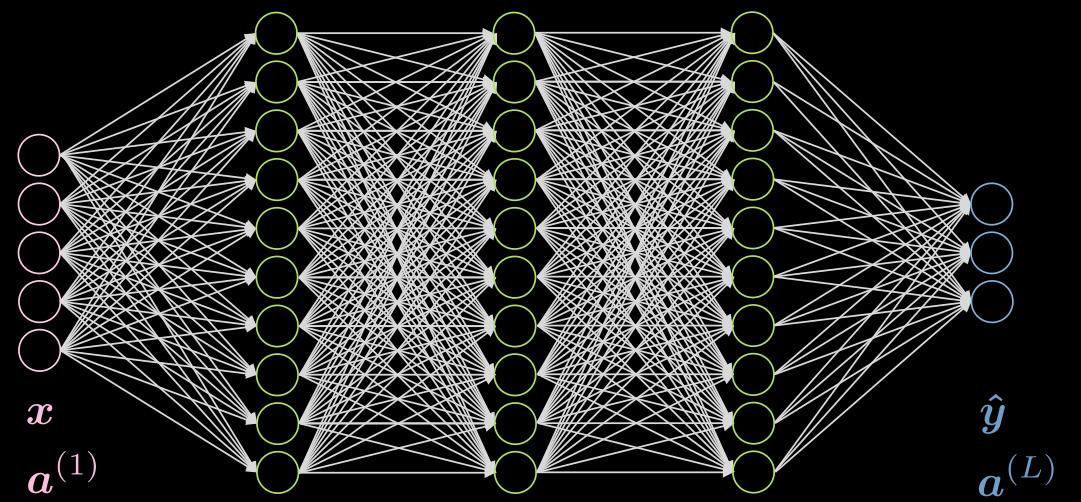
الشكل 1: شبكة متصلة بالكامل

إذا كانت بياناتنا تعرض مكانًا محليًا، فكل خلية عصبية تحتاج إلى الاتصال ببضعة خلايا عصبية محلية فقط من الطبقة السابقة. وبالتالي، يمكن إسقاط بعض الاتصالات كما هو موضح في الشكل 2. يمثل الشكل 2 (أ) شبكة تامة الاتصال FC. الاستفادة من الخاصية المحلية لبياناتنا، نقوم بإسقاط الاتصالات بين الخلايا العصبية البعيدة في الشكل 2 (ب). على الرغم من أن الخلايا العصبية المخفية (باللون الأخضر) في الشكل 2 (ب) لا تغطي المدخلات بالكامل، فإن الهيكل العام سيكون قادرًا على حساب جميع الخلايا العصبية المدخلة. المجال الاستقبالي (RF) هو عدد الخلايا العصبية في الطبقات السابقة، والتي يمكن لكل خلية عصبية في طبقة معينة رؤيتها أو أخذها في الاعتبار. لذلك، فإن RF للطبقة المخرجة باعتبار الطبقة المخفية هي 3، RF للطبقة المخفية باعتبار الطبقة المدخلة هي 3، لكن RF للطبقة الناتجة باعتبار طبقة الإدخال هي 5.

الشكل 2 (أ): قبل تطبيق التباين	الشكل 2 (ب): بعد تطبيق التباين

الثبات $\Leftarrow$ مشاركة المتغيرات.

إذا كانت بياناتنا تعرض حالة ثابتة، فيمكننا استخدام مجموعة صغيرة من المتغيرات عدة مرات عبر بنية الشبكة. على سبيل المثال في شبكتنا المتفرقة، الشكل 3(أ)، يمكننا استخدام مجموعة من 3 متغيرات مشتركة (الأصفر والبرتقالي والأحمر). ثم سينخفض ​​عدد المعلمات من 9 إلى 3! قد تعمل البنية الجديدة بشكل أفضل لأن لدينا المزيد من البيانات لتدريب تلك الأوزان المحددة. تسمى الأوزان بعد تطبيق التباين ومشاركة المعلمات نواة الالتفاف.

الشكل 3 (أ): قبل تطبيق مشاركة المعلمات	الشكل 3 (ب): بعد تطبيق مشاركة المعلمات

فيما يلي بعض مزايا استخدام التباين ومشاركة المعلمات: -

• مشاركة المتغيرات
  • تقارب أسرع
  • تعميم أفضل
  • غير معتمد على حجم الإدخال
  • استقلال نواة الالتفاف $\Leftarrow$ زيادة المعالجة على التوازي
• الاتصال المتناثر
  • تقليل مقدار الحوسبة

يوضح الشكل 4 مثالاً على حبات على بيانات 1D، حيث يكون حجم النواة: 2 (عدد النوى) * 7 (سمك الطبقة السابقة) * 3 (عدد التوصيلات / الأوزان الفريدة).

اختيار حجم النواة تجريبي. يبدو أن الالتفاف 3 * 3 هو الحجم الأدنى للبيانات المكانية. يمكن استخدام الالتفاف بالحجم 1 للحصول على طبقة نهائية يمكن تطبيقها على صورة إدخال أكبر. قد يقلل حجم النواة للأرقام الزوجية من جودة البيانات، وبالتالي لدينا دائمًا حجم نواة للأرقام الفردية، عادةً 3 أو 5.

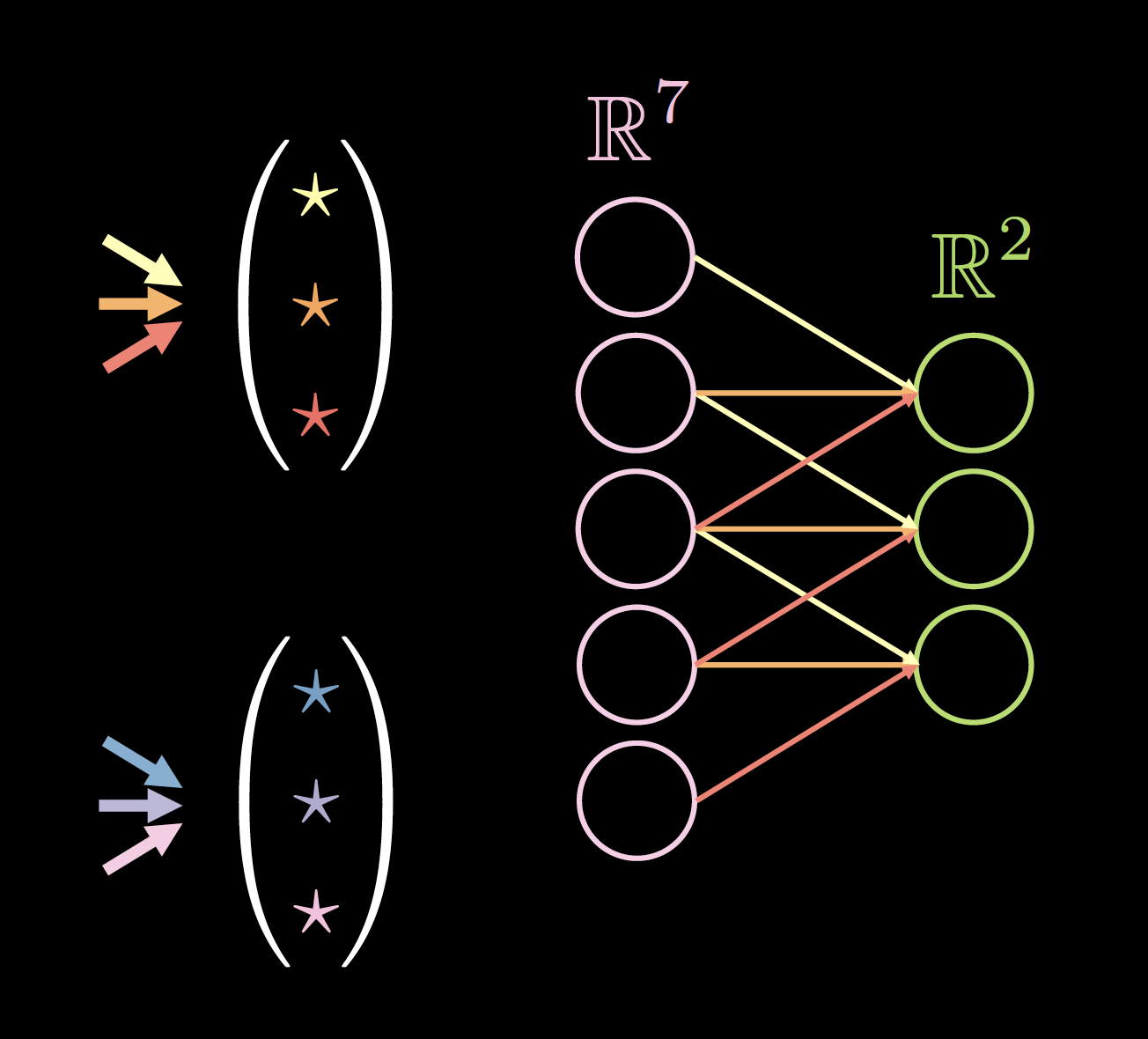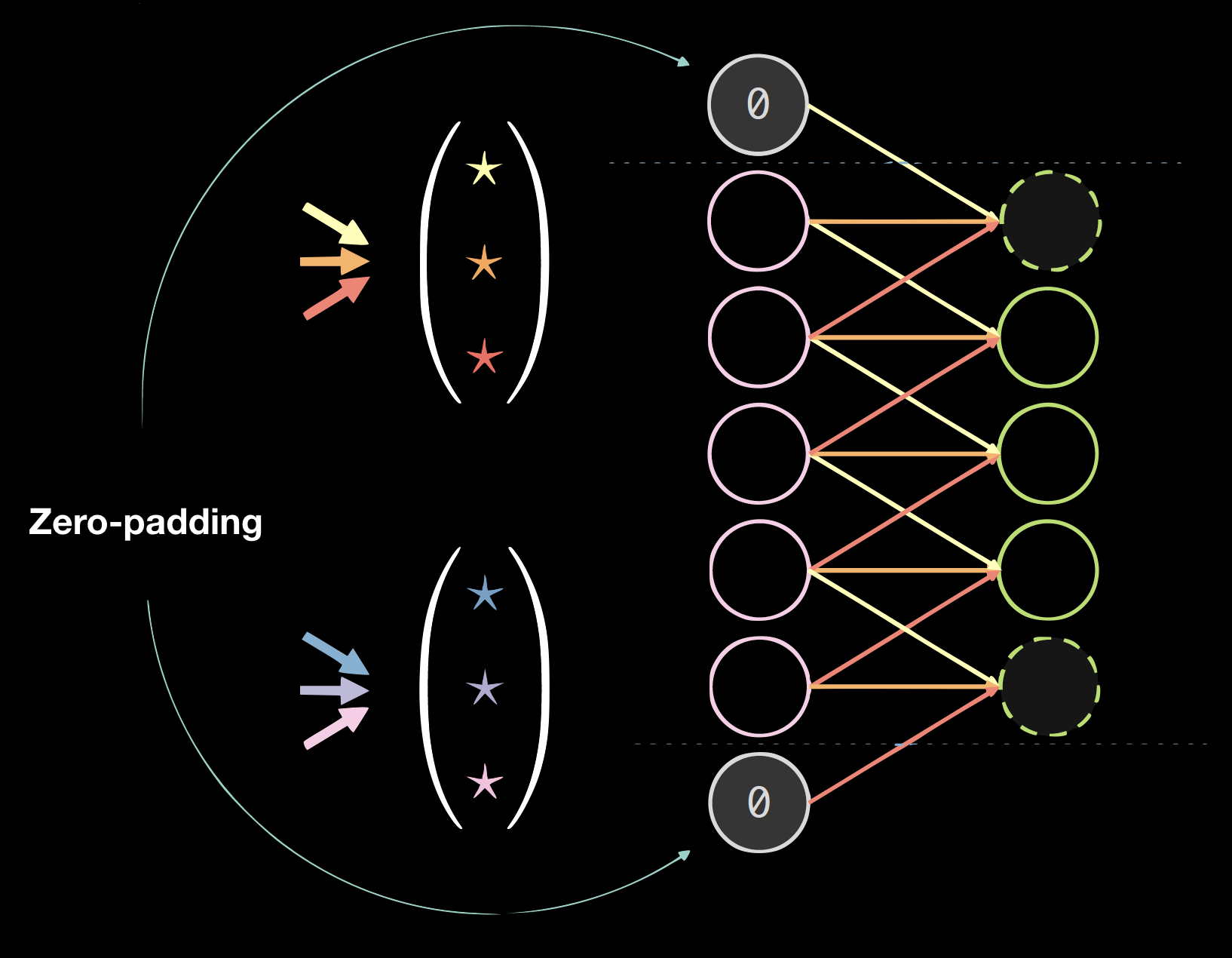الشكل 4 (أ): نواة على بيانات 1D	الشكل 4 (ب): بيانات ذات مساحة صفرية

تبطين

يؤدي التبطين عمومًا إلى إضرار النتائج النهائية، ولكنه مناسب برمجيًا. نستخدم عادةً حشوة صفرية: size = (kernel size - 1)/2.

الشبكات الالتفافية المعيارية

يحتوي CNN المكاني القياسي على الخصائص التالية:

• طبقات متعددة
  • الالتفافية
  • الدول اللاخطية (ReLU و Leaky)
  • التجميع
  • تطبيع الحزمة
• اتصال الالتفافية المتبقية

تعد تسوية الحزمات واتصالات التجاوز المتبقية مفيدة جدًا في جعل الشبكة تتدرب جيدًا. يمكن أن تضيع أجزاء من الإشارة إذا تم تكديس العديد من الطبقات، لذا فإن التوصيلات الإضافية عبر التجاوز المتبقي تضمن مسارًا من الأسفل إلى الأعلى وأيضًا لمسار التدرجات القادمة من أعلى إلى أسفل.

في الشكل 5، بينما تحتوي صورة الإدخال في الغالب على معلومات مكانية عبر بعدين (بصرف النظر عن المعلومات المميزة، وهي لون كل بكسل)، فإن طبقة الإخراج سميكة. في منتصف الطريق، هناك مفاضلة بين المعلومات المكانية والمعلومات المميزة ويصبح التمثيل أكثر كثافة. لذلك، مع تقدمنا ​​في التسلسل الهرمي، نحصل على تمثيل أكثر كثافة حيث نفقد المعلومات المكانية.

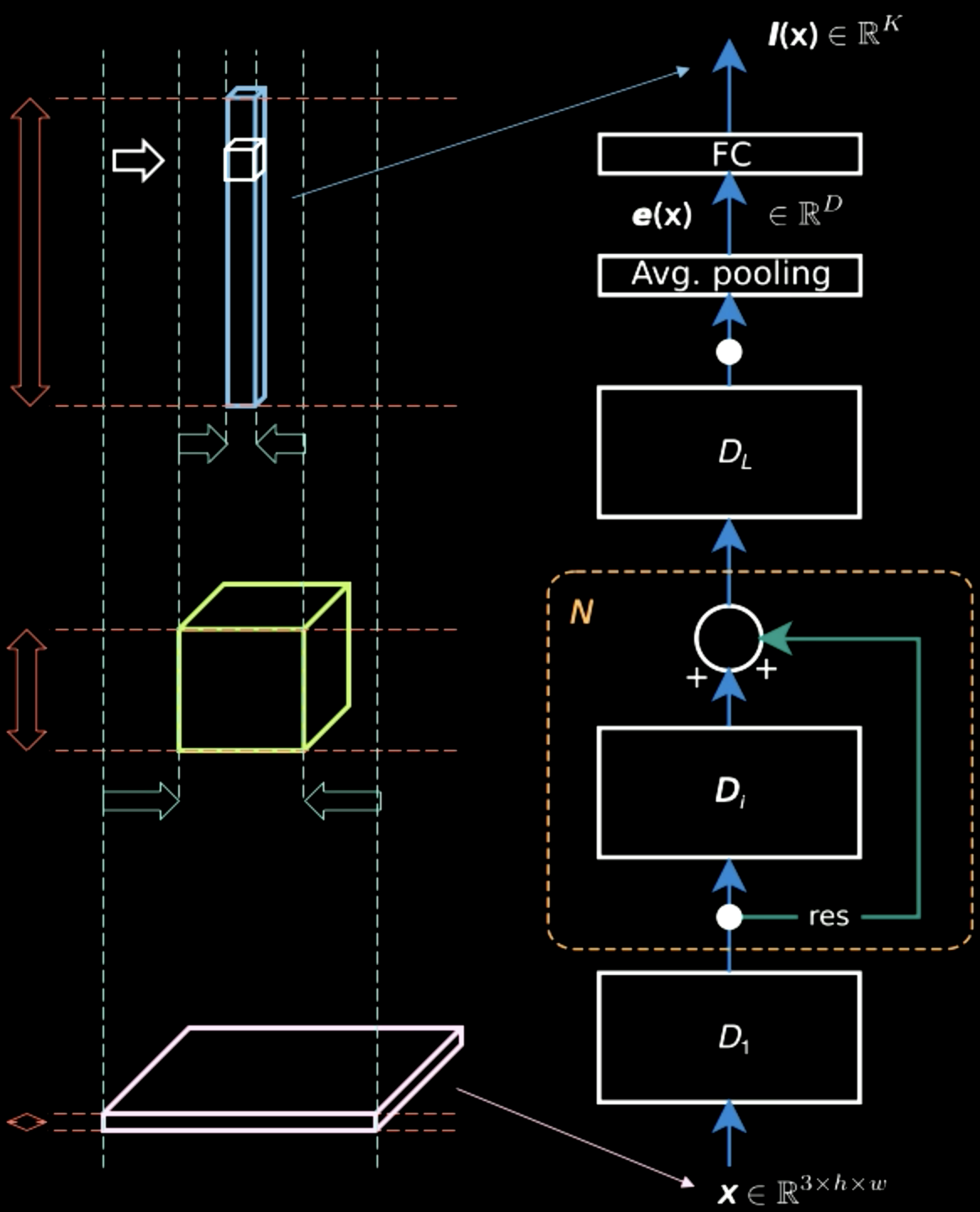
الشكل 5: تمثيلات المعلومات تتقدم في التسلسل الهرمي

التجميع

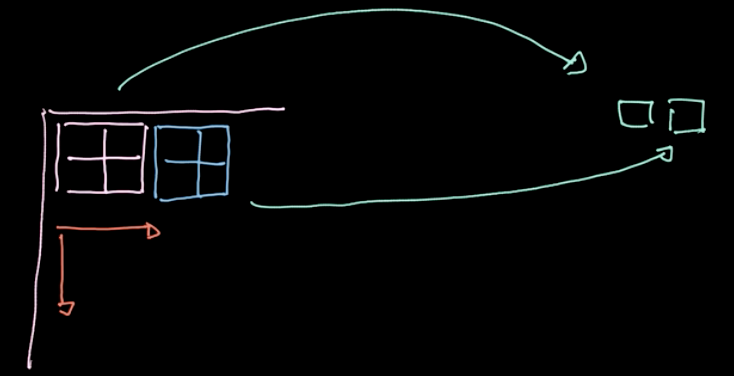
الشكل 6: رسم توضيحي للتجميع

يتم تطبيق عامل معين، $L_p$-norm، على مناطق مختلفة (راجع الشكل 6). يعطي عامل التشغيل هذا قيمة واحدة فقط لكل منطقة (قيمة واحدة لـ 4 بكسل في مثالنا). ثم نقوم بتكرار هذه العملية عبر منطقة البيانات بأكملها منطقة تلو الأخرى، واتخاذ خطوات بناءً على الخطوة. إذا بدأنا بـ $m * n$ data بقنوات $c$، فسننتهي بـ $\frac {m} {2} * \frac {n} {2}$ data مع قنوات $c$ (راجع الشكل 7). التجميع ليس محددًا ؛ ومع ذلك، يمكننا اختيار أنواع مختلفة من الاقتراع مثل التجميع الأقصى ومتوسط ​​التجميع وما إلى ذلك. الغرض الرئيسي من التجميع يقلل من كمية البيانات حتى نتمكن من الحساب في فترة زمنية معقولة.

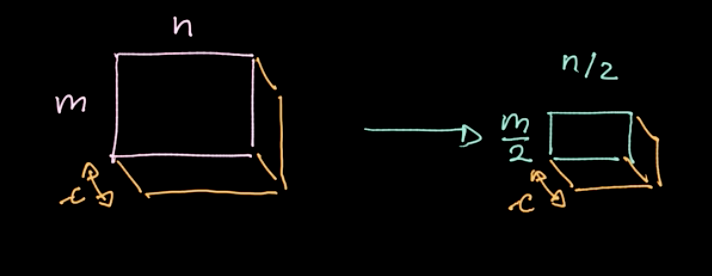
الشكل 7: تجميع النتائج

الشبكات الاتفافية - Jupyter Notebook

يمكن العثور على Jupyter Notebook هنا. لتشغيل Jupyter Notebook، تأكد من تثبيت بيئة pDL على النحو المحدد في README.md .

في هذا الكمبيوتر الدفتري، نقوم بتدريب شبكة متعدد الطبقات (شبكة FC) وشبكة عصبية التفافية (CNN) لمهمة التصنيف في مجموعة بيانات MNIST. لاحظ أن كلا الشبكتين لهما عدد متساوٍ من المعلمات. (الشكل 8)

الشكل 8: مثيلات من مجموعة بيانات MNIST الأصلية

قبل بدأ عملية التعليم، نقوم بتطبيع بياناتنا بحيث تتناسب تهيئة الشبكة مع توزيع البيانات لدينا (مهم جدًا!). تأكد أيضًا من أن العمليات / الخطوات الخمس التالية موجودة في عملية التعليم:

1. تغذية البيانات إلى المعمارية
2. حساب دالة الفرق
3. تنظيف ذاكرة التخزين المؤقت للتدرجات المتراكمة بـ zero_grad ()
4. حساب التدرجات
5. تنفيذ خطوة في طريقة المحسن

أولاً، نقوم بتدريب كلتا الشبكتين على بيانات MNIST الطبيعية. تبين أن دقة شبكة FC بلغت $87\%$ بينما تبين أن دقة شبكة CNN بلغت $95\%$. نظرًا لنفس العدد من المعلمات، تمكنت CNN من تدريب العديد من المرشحات. في شبكة FC، يتم تدريب المرشحات التي تحاول الحصول على بعض التبعيات بين الأشياء البعيدة عن الأشياء القريبة. لقد ضاعوا تماما. بدلاً من ذلك، في الشبكة التلافيفية، تركز كل هذه المعلمات على العلاقة بين وحدات البكسل المجاورة.

بعد ذلك، نقوم بإجراء تبديل عشوائي لجميع وحدات البكسل في جميع صور مجموعة بيانات MNIST الخاصة بنا. هذا يحول الشكل 8 لدينا إلى الشكل 9. ثم نقوم بتدريب كلتا الشبكتين على مجموعة البيانات المعدلة هذه.

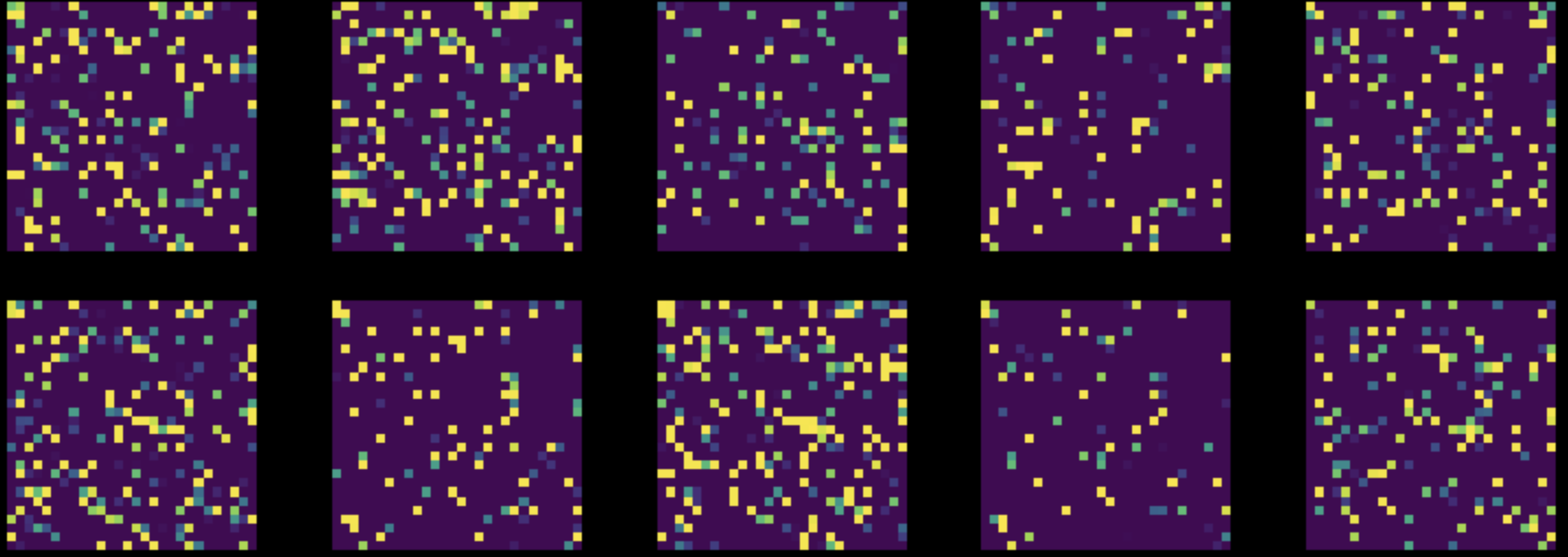
الشكل 9: </ b> مثيلات من مجموعة بيانات MNIST المتغيرة </center> ظل أداء شبكة FC دون تغيير تقريبًا ($85\%$)، لكن دقة CNN انخفضت إلى $83\%$. هذا لأنه، بعد التقليب العشوائي، لم تعد الصور تحمل الخصائص الثلاثة للموقع، والثبات، والتكوين، التي يمكن لشبكة CNN استغلالها.