.الشبكات الالتفافية تطورها, معماريتها, تفاصيل التطبيق البرمجي ومميزاتها

النماذج الأولية للشبكات الالتفافية وتطورها

تطبيق الشبكات العصبية البدائية على مجموعات من البيانات الصغيرة

طورت أول طُورت أول CNN والمستوحاة من عمل البرفيسور فوكوشيما في نمذجة القشرة البصرية، وباستخدام تركيب هرمي من الوحدات العصبية الصناعية البسيطة و المعقدة، جنبًا إلى جنب مع التدريب الخاضع للإشراف و خوارزمية الانتشار العكسي في جامعة تورنتو ما بين عامي 1988-1989 بواسطة البروفيسور Yann LeCun. استخدمت التجارب مجموعة بيانات صغيرة من 320 رقمًا.

تمت مقارنة أداء البنى التالية:-

1. طبقة واحدة تامة الاتصال

2. طبقتان متصلتان

3. طبقات متصلة محليًا بدون أوزان مشتركة

4. شبكة مقيدة مع أوزان مشتركة واتصالات محلية

5. شبكة مقيدة مع أوزان مشتركة واتصالات محلية 2 (بالمزيد من نماذج الخصائص)

تتمتع أكثر الشبكات نجاحاً (الشبكة المقيدة ذات الأوزان المشتركة) بأقوى قابلية للتعميم وتشكل الأساس للـ CNN الحديثة، بينما تميل الطبقة تامة الاتصال إلى فرط التخصيص.

أول ConvNets “حقيقية” في Bell Labs

بعد إنتقاله إلى Bell Labs، تحول عمل LeCunn إلى استخدام الرموز البريدية المكتوبة بخط اليد عن طريق خدمة البريد الأمريكية لتدريب CNN أكبر:

• طبقة مدخلات بسعة 256 تسمح لصورة بحجم (16$\times$16).
• 12 (5$\times$5) مرشح بخطوة انتقالية مقدارها 2 بيكسل , لتقليل دقة الطبقة اللاحقة.
• لم يتم استخدام أي نوع من انواع التجميع (pooling).

معمارية الشبكات الالتفافية مع التجميع

في العام التالي، تم إجراء بعض التغييرات على معمارية الشبكات الالتفافية: منها تقديم التجميع المنفصل. حيث يتم تجميع قيم المدخلات عن طريق حساب متوسط ​​قيم الإدخال وإضافة قيمة معامل الانحياز، وتمريرهم إلى دالة غير خطية (دالة الظل المماسية). عملية التجميع تتم على مساحة (2$\times$2) بخطوة انتقالية مقدارها 2 بيكسل، وبالتالي تقليل دقة الصورة المدخلة بمقدار النصف.

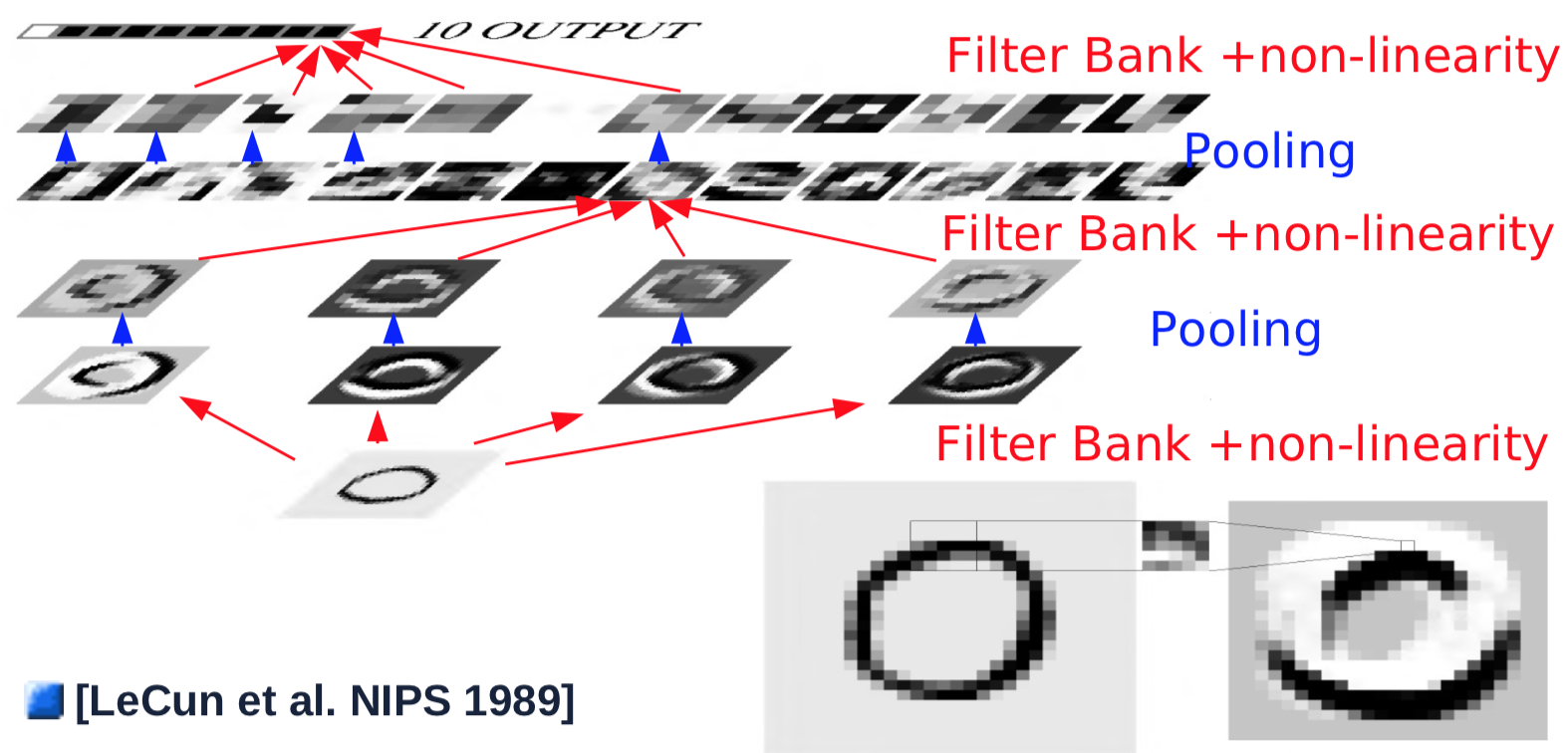
شكل 1. معمارية الشبكات الالتفافية

مثال على طبقة واحدة من الشبكات الالتفافية سيكون كما يلي:

1. خذ مُدخلاً بحجم 32$\times$32
2. تقوم الطبقة الالتفافية بتمرير مرشح بحجم 5$\times$5 مع خطوة إنتقالية مقدارها 1 بيكسل على مساحة الصورة، ينتج عنها ربط الخصائص مقداره 28$\times$28.
3. مرر نموذج ربط الخصائص إلى دالة غير خطية: حجمها 28$\times$28.
4. مرره إلى طبقة التجميع، حيث تقوم بحساب المتوسط على مساحة 2$\times$2 بخطوة إنتقالية مقدارها 2 بيكسل: حجمه 14$\times$14.
5. يتم تكرار الخطوات السابقة من 1 إلى 4 لـ 4 مرشحات.

المرحلة الاولى، مكونة من طبقة (التفافية وتجميعية) عادة تقوم باكتشاف الخصائص البسطية في الصورة المدخلة، مثل التعرف على الحواف والحدود للأشكال الموجودة في الصورة. بعد المرحلة الاولى يكون الهدف هو التعرف على مجوعة اكثر تعقيدا من خصائص الصورة، عن طريق تجميع الخصائص البسيطة التي تم اكتشافها في المرحلة السابقة. للتمكن من تحقيق ذلك يتم تكرار الخطوات من 2 إلى 4 بمرشحات مختلفة، بتمريرها على نماذج ربط الخصائص الناتجة من المرحلة السابقة يتم تجميع الناتج كنموذج تنشيط جديد.

1. يتم تمرير مرشح جديد بحجم 5$\times$5 على جميع نماذج ربط الخصائص السابقة مع تجميع الناتج (لاحظ ان البرفيسور LeCun في تجاربه السابقة التي اجراها في عام 1989 الطبقات لم تكن تامة الاتصال لاسباب لها علاقة بالقدرة الحاسوبية المتوفرة في هذا الوقت، لكن في الوقت الحالي يتم تأكيد الاتصال بين الطبقات ) يكون الناتج مقداره 10$\times$10.
2. مرر الناتج من الطبقة الالتفافية لدالة غير خطية يكون الناتج مقداره 10$\times$10.
3. اعد تكرار الخطوة 1/2 مع 16 مرشح.
4. مرر الناتج لطبقة التجميع لتقوم بحساب متوسط القيم على مساحة 2$\times$2 بخطوة انتقالية مقدارها 2، ليكون الناتج بعد هذه العملية مقداره 5$\times$5 لكل نموذج ربط خصائص.

لإنتاج المخرجات، يتم تنفيذ الطبقة الأخيرة من عملية الالتفاف، والتي تبدو وكأنها وصلات كاملة ولكنها في الواقع التفافية.

1. يتم تمرير مرشح جديد بحجم 5$\times$5 على جميع نماذج ربط الخصائص السابقة مع تجميع الناتج يكون الناتج مقداره 1$\times$1.
2. مرر الناتج من الطبقة الالتفافية لدالة غير خطية يكون الناتج مقداره 1$\times$1.
3. يتم إنتاج قيمة خارج واحد لكل فئة.
4. تعاد جميع الخطوات السابقة لكل فئة من فئات الخارج على التوازي.

شاهد هذه الرسوم المتحركة على موقع Andrej Karpathy على الويب للتعرف على كيفية تغيير الطبقة الالتفافية لشكل نماذج ربط الخصائص للطبقة التالية. يمكن العثور على الورقة الكاملة هنا.

الإزاحة متساوية التغير

شكل 2. الإزاحة متساوية التغير

كما هو موضح من خلال الرسوم المتحركة على الشرائح (إليك مثال آخر)، فإن إزاحة الصورة المدخلة ينتج عنها نفس الإزاحة لنماذج الخصائص. ومع ذلك، يتم قياس التغييرات في نماذج الخصائص من خلال عمليات الالتفاف / التجميع. على سبيل المثال تجميع 2$\times$2 مع خطوة انتقالية 2 سيقلل إزاحة 1 بكسل في طبقة الإدخال إلى 0.5 بكسل إزاحة في نماذج الخصائص التالية. يتم بعد ذلك استبدال الدقة المكانية لزيادة عدد أنواع الخصائص، أي جعل التمثيل أكثر تجريدًا وأقل حساسية للتحولات والتشوهات.

تحليل إجمالي للمعمارية

يمكن تحليل المعمارية العامة للـ CNN لمجموعة من الطبقات الاساسية كما يلي:

• التسوية المعيارية
  • ضبط التبييض الإحصائي (اختياري)
  • الطرق الطرحية على سبيل المثال إزالة المتوسط، ترشيح للترددات العالية
  • الطرق التَقسِيمِيّة: تطبيع أو تسوية التَبايُنٌ المحلي، تسوية التفاوت

• حزمة الترشيح
  • زيادة الابعاد
  • الإسقاط على أساس عياري متعامد
  • التعرف على الحواف وحدود الاشكال في الصور

• الدوال اللاخطية
  • التنثير (تحويل القيم إلى مصفوفة متناثرة)
  • وحدة خطية مصححة نموذجية (ReLU): $\text{ReLU}(x) = \max(x, 0)$

• التجميع
  • تجميع نماذج الخصائص
  • تجميع القيم الاعلى $\text{MAX}= \text{Max}_i(X_i)$
  • تجميع على الفضاء المعياري LP-Norm $\text{L}p= \left(\sum_{i=1}^n \|X_i\|^p \right)^{\frac{1}{p}}$
  • التجميع اللوغاريثمي $\text{Prob}= \frac{1}{b} \left(\sum_{i=1}^n e^{b X_i} \right)$

التعرف على الأرقام باستخدام LeNet5

تطبيق برمجي لمعمارية LeNet5 باستخدام Pytorch

تتكون معمارية LeNet5 من الطبقات التالية بداية من اعلى إلى اسفل :-

1. Log-Softmax
2. طبقة واحدة تامة الاتصال ابعادها 500$\times$10.
3. ReLu
4. طبقة واحدة تامة الاتصال ابعادها (4$\times$4$\times$50)$\times$500
5. طبقة تجميع القيم الاعلى بحجم 2$\times$2 مع خطوة انتقالية مقدارها 2 بيكسل.
6. ReLu
7. طبقة التفافية بقيمة خارج 20 قناة، مرشح 5$\times$5 مع خطوة انتقالية مقدارها 1 بيكسل.
8. طبقة تجميع القيم الاعلى بحجم 2$\times$2 مع خطوة انتقالية مقدارها 2 بيكسل.
9. ReLu
10. طبقة التفافية بقيمة خارج 20 قناة، مرشح 5$\times$5 مع خطوة انتقالية مقدارها 1 بيكسل.

قيمة الدخل للمعمارية 32$\times$32 بيكسل على رمادية تدرج الالوان وقناة واحدة.

تطبيق برمجي لمعمارية LeNet5 باستخدام Pytorch

class LeNet5(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.conv2 = nn.Conv2d(20, 20, 5, 1)
        self.fc1 = nn.Linear(4*4*50, 500)
        self.fc2 = nn.Linear(500, 10)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.max_pool2d(x, 2, 2)
        x = F.relu(self.conv2(x))
        x = F.max_pool2d(x, 2, 2)
        x = x.view(-1, 4*4*50)
        x = F.relu(self.fc1)
        x = self.fc2(x)
    return F.logsoftmax(x, dim=1)

على الرغم من ان fc1 و fc2 طبقات تامة الاتصال، إلا ان يمكن اعتبارهم طبقة التفافية ذات مرشح يغطي الصورة باكملها. يتم استخدام طبقات تامة الاتصال لأسباب مرتبطة بالفاعلية.

يمكن انتاج نفس المعمارية في Pytorch باستخدام nn.Sequential.

ميزات الـ CNN

في الشبكة الالتفافية الكاملة، ليست هناك حاجة لتحديد حجم المدخلات. ومع ذلك، فإن تغيير حجم الإدخال يغير حجم المخرجات.

خذ بعين الاعتبار نظام التعرف على الكتابة بخط اليد. لا يتعين علينا تقسيم صورة الإدخال إلى شرائح. يمكننا تطبيق CNN على الصورة بأكملها: ستغطي المرشحات جميع المواقع في الصورة بأكملها وتسجيل نفس الإخراج بغض النظر عن مكان وجود النمط. يعد تطبيق CNN على صورة كاملة أرخص بكثير من تطبيقه في مواقع متعددة بشكل منفصل. ليس هناك حاجة إلى تجزئة مسبقة، وهو أمر مريح لأن مهمة تجزئة الصورة مكلفة للغاية.

مثال: MNIST

تم تدريب LeNet5 على صور MNIST بحجم 32$\times$32 لتصنيف الأرقام المنفردة في وسط الصورة. تم تطبيق زيادة البيانات عن طريق إزاحة الرقم في اتجاهات مختلفة، وتغيير حجم الرقم، وإدخال الأرقام في الجانب. كما تم تدريبها بالفئة الحادية عشرة التي لم تمثل أيًا مما سبق. تم إنشاء الصور التي تم تصنيفها بواسطة هذه الفئة إما عن طريق إنتاج صور فارغة، أو وضع أرقام على الجانب وليس المركز.

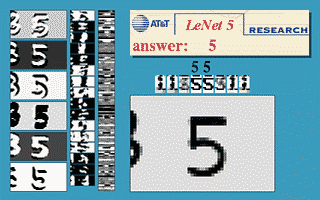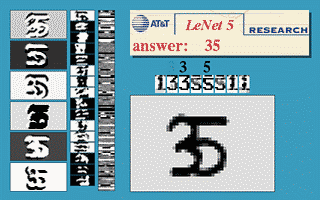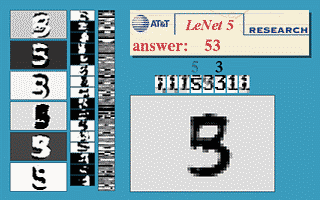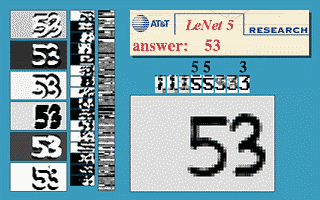
شكل 3. نافذة إزاحة التفافية

توضح الصورة أعلاه أن شبكة LeNet5 المدربة على 32$\times$32 يمكن تطبيقها على صورة 32$\times$64 للتعرف على الرقم في مواقع متعددة.

مشكلة ربط الخصائص

ما هي مشكلة ربط الخصائص؟

يواجه علماء الرؤية الاعصاب البصرية ورؤية الكمبيوتر مشكلة تحديد الكائن ككائن. الكائن عبارة عن مجموعة من الخصائص، ولكن كيف يتم ربط جميع الخصائص لتشكيل هذا الكائن؟

كيف يمكن حل هذه المشكلة؟

يمكننا حل مشكلة ربط الخصائص هذه باستخدام بمعمارية CNN بسيط للغاية: طبقتان فقط من لالتفافية مع التجميعات بالإضافة إلى طبقتين آخرتين متصلتين بالكامل بدون أي آلية محددة لذلك، نظرًا لأن لدينا ما يكفي من البيانات ودول غير خطية لتدريب CNN الخاص بنا.

شكل 4. حل مشكلة ربط الخصائص باستخدام شبكة التفافية

تُظهر الرسوم المتحركة أعلاه قدرة CNN على التعرف على الأرقام المختلفة عن طريق تحريك ضربة واحدة حولها، مما يدل على قدرتها على معالجة مشاكل ربط الخصائص، أي التعرف على الخصائص بطريقة هرمية وتركيبية.

مثال: مدخلات متغيرة الابعاد

يمكننا بناء CNN بطبقتين من الالتفافية بخطوة انتقالية مقدارها 1 بيكسل، مع طبقتين للتجميع مع خطوة انتقالية مقدارها 2 بيكسل بحيث تكون الخطوة الإجمالية 4. وبالتالي، إذا أردنا الحصول على مخرجات جديدة، فنحن بحاجة إلى إزاحة نافذة الإدخال بمقدار 4. بشكل أكثر وضوحا، يمكننا أن نرى الشكل أدناه (الوحدات الخضراء). أولاً، لدينا إدخال بحجم 10، ونقوم بإجراء التفاف بمرشح بالحجم 3 للحصول على 8 وحدات. بعد ذلك، نقوم بتجميع الحجم 2 للحصول على 4 وحدات. وبالمثل، نكرر الالتفاف والتجميع مرة أخرى، وفي النهاية نحصل على ناتج واحد.

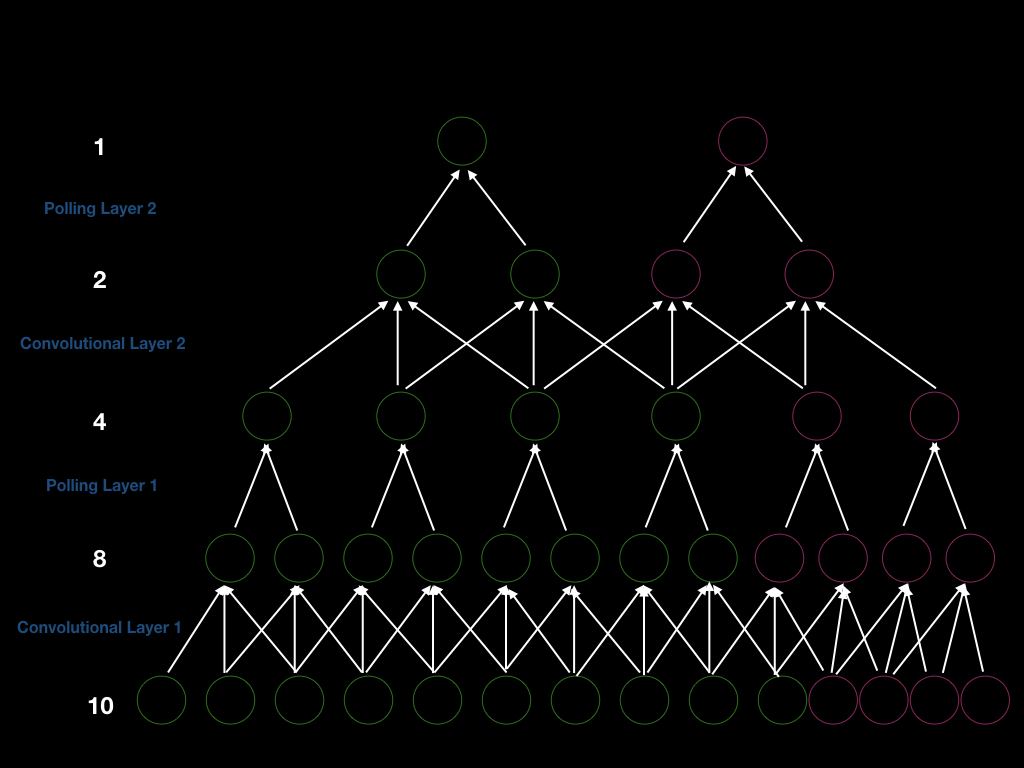
شكل 5. معمارية شبكة التفافية بمدخلات متغيرة الابعاد

لنفترض أننا أضفنا 4 وحدات في طبقة الإدخال (الوحدات الوردية أعلاه)، حتى نتمكن من الحصول على 4 وحدات أخرى بعد طبقة الالتفاف الأولى، ووحدتين أخريين بعد طبقة التجميع الأولى، ووحدتين أخريين بعد طبقة الالتفاف الثانية، و 1 مخرج جديد.

لذلك، حجم النافذة لإنشاء مخرجات جديدة هو 4 (خطوتان $\times$2) علاوة على ذلك، هذا دليل على حقيقة أننا إذا قمنا بزيادة حجم المدخلات، فسنزيد حجم كل طبقة، مما يثبت قدرة الـ CNN على التعامل مع مدخلات متغيرة الابعاد.

فيما تفيد الشبكات الالتفافية؟

تعد الـ CNN جيدة للإشارات الطبيعية التي تأتي في شكل مصفوفات متعددة الأبعاد ولها ثلاث خصائص رئيسية:

1. المحلية: الميزة الاولى هو وجود ارتباط محلي قوي بين القيم. إذا أخذنا بكسلين قريبين من صورة طبيعية، فمن المحتمل جدًا أن يكون لتلك البكسلات نفس اللون. عندما تصبح وحدات البكسل متباعدة، سيقل التشابه بينهما. يمكن أن تساعدنا الارتباطات المحلية في اكتشاف الميزات والخصائص المحلية، وهو ما تفعله الـ CNN. إذا قمنا بتغذية CNN بوحدات البكسل التي تم اعادة فرزها بعشوائية، فلن تعمل بشكل جيد في التعرف على الصور المدخلة، بينما لن تتأثرالشبكات تامة الاتصال FC. الارتباط المحلي يبرر الاتصالات المحلية.
2. استقرار الاشارة: الميزة الثانية هو أن الخصائص ضرورية ويمكن أن تظهر في أي مكان على الصورة، مما يبرر الأوزان المشتركة والتجميع. علاوة على ذلك، يتم توزيع الإشارات الإحصائية بشكل موحد، مما يعني أننا بحاجة إلى تكرار اكتشاف نفس الخاصية لكل موقع في صورة الإدخال.
3. التراكبية: الميزة الثالثة أن الصور الطبيعية تركيبية، بمعنى أن الخصائص تؤلف الصورة بطريقة هرمية. هذا يبرر استخدام طبقات متعددة من الخلايا العصبية، والتي تتوافق أيضًا بشكل وثيق مع أبحاث Hubel و Weisel حول الخلايا البسيطة والمعقدة

علاوة على ذلك، يستفاد بشكل جيد من الـ CNN في مقاطع الفيديو والصور والنصوص والتعرف على الكلام.