تصور عملية تحويل المعاملات للشبكات العصبية والمفاهيم الأساسية للالتفاف

تصور الشبكات العصبية

في هذا الجزء سوف نتخيل العملية الداخلية للشبكة العصبية.

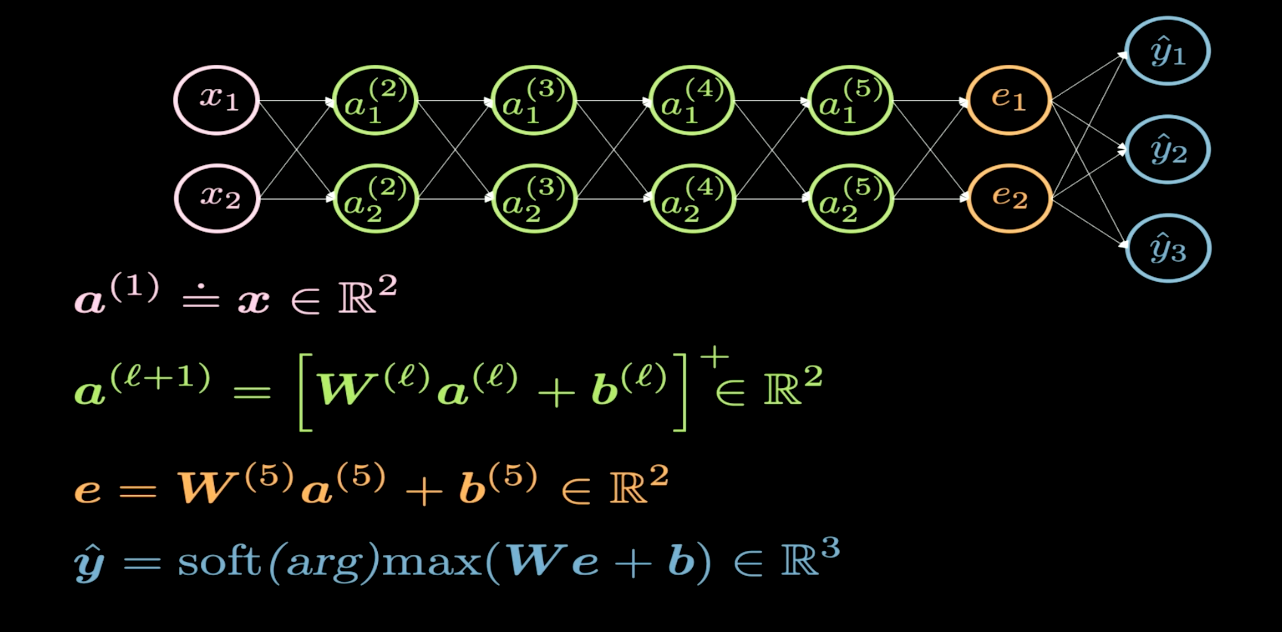
شكل 1 هيكل الشبكة

يصور شكل 1 بنية الشبكة العصبية التي نرغب في تصورها. عادةً، عندما نرسم بنية الشبكة العصبية، يظهر الإدخال في الأسفل أو على اليسار، ويظهر الناتج في الجانب العلوي أو على اليمين. في الشكل 1، تمثل الخلايا العصبية باللون الوردي المدخلات، وتمثل الخلايا العصبية الزرقاء المخرجات. في هذه الشبكة، لدينا 4 طبقات مخفية (باللون الأخضر)، مما يعني أن لدينا 6 طبقات في المجموع (4 طبقات مخفية + طبقة إدخال واحدة + طبقة إخراج واحدة). في هذه الحالة، لدينا 2 من الخلايا العصبية لكل طبقة مخفية، وبالتالي فإن أبعاد مصفوفة الوزن ($W$) لكل طبقة هي 2 $\times$ 2. هذا لأننا نريد تحويل سطح أو مستوى الإدخال إلى مستوى آخر يمكننا تخيله.

شكل 2 تصور المساحة القابلة للطي

تشبه عملية تحويل كل طبقة بطي السطح الخاص بنا في بعض المناطق المحددة كما هو موضح في الشكل 2. هذه الطيات حادة للغاية، وذلك لأن جميع التحويلات تتم في الطبقة ثنائية الأبعاد. في التجربة، وجدنا أنه إذا كان لدينا خليتان فقط في كل طبقة مخفية، فإن التحسين سيستغرق وقتًا أطول؛ يسهل التحسين إذا كان لدينا المزيد من الخلايا العصبية في الطبقات المخفية. هذا يتركنا مع سؤال مهم: لماذا يصعب تدريب الشبكة بعدد أقل من الخلايا العصبية في الطبقات المخفية؟ يجب أن تفكر في هذا السؤال بنفسك وسنعود إليه بعد تخيل $\texttt{ReLU}$.

(أ)	(ب)

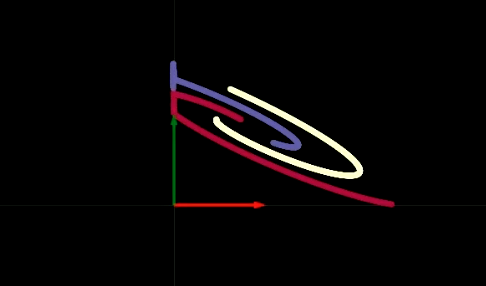
عندما نعبر الشبكة بالمرور على طبقة مخفية واحدة في كل مرة، نرى أنه مع كل طبقة نقوم بنوع من التحويل التآلفي (affine transformation) متبوعًا بتطبيق عملية ReLU غير الخطية، والتي تتخلص من أي قيم سلبية. في الشكلين 3 (أ) و (ب) ، يمكننا أن نرى تصور عامل ReLU. يساعدنا عامل ReLU على القيام بتحولات غير خطية. بعد خطوات متعددة لإجراء تحويل تآلفي متبوعًا عامل ReLU، يمكننا في النهاية فصل البيانات خطيًا كما هو موضح في شكل 4.

شكل 4 تصور المخرجات

يوفر لنا ما ذكرناه بعض الأفكار حول سبب صعوبة تدريب الطبقات المخفية المكونة من خليتين عصبيتين فقط. تحتوي شبكتنا المكونة من 6 طبقات على تحيز واحد في كل طبقة مخفية. لذلك، إذا نقل أحد هذه التحيزات أي من النقاط إلى خارج الربع العلوي الأيمن، فإن تطبيق عامل ReLU سيقضي على هذه النقاط إلى الصفر. بعد ذلك، بغض النظر عن كيفية تحويل الطبقات للبيانات لاحقًا، ستبقى القيم لتلك النقاذ بصفر. يمكننا أن نجعل تدريب الشبكة العصبية أسهل عن طريق جعل الشبكة “أكثر بدانة” - أي إضافة المزيد من الخلايا العصبية في الطبقات المخفية - أو يمكننا إضافة المزيد من الطبقات المخفية، أو مزيج من الطريقتين. خلال هذه الدورة التدريبية، سوف نستكشف كيفية تحديد أفضل بنية شبكة لمشكلة معينة، ترقبوا ذلك.

تحويل المعاملات

معنى تحويل المعاملات أن متجه المعاملات $w$ هو ناتج لدالة. من خلال هذا التحويل، يمكننا تعيين فضاء المعاملات الأصلية إلى فضاء آخر. في الشكل 5، $w$ هو ناتج $H$ بالمعامل $u$. $G(x,w)$ هي عبارة عن شبكة و $C(y,\bar y)$ هي دالة تكلفة. تتكيف أيضًا صياغة الانتشار الخلفي على النحو التالي،

يتم تطبيق هذه الصيغ على شكل مصفوفة. لاحظ أن أبعاد العناصر يجب أن تكون متسقة. أبعاد $u$، $w$، $\frac{\partial H}{\partial u}^\top$، $\frac{\partial C}{\partial w}^\top$، تساوي $[N_u \times 1]$، $[N_w \times 1]$، $[N_u \times N_w]$، $[N_w \times 1]$، على التوالي. لذلك، أبعاد صيغة الانتشار الخلفي لدينا متسقة.

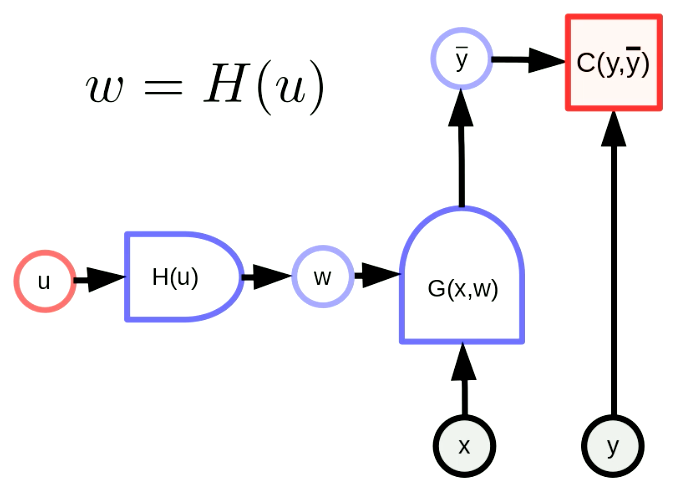
شكل 5 الشكل العام لتحويل المعاملات

تحويل بسيط للمعاملات: مشاركة الأوزان

تحويل مشاركة الأوزان يعني أن $H(u)$ تنسخ عنصرًا واحدًا من $u$ إلى عناصر متعددة لـ $w$. تشبه $H(u)$ فرع Y لنسخ $u_1$ إلى $w_2$، $w_1$. يمكن التعبير عن هذا على النحو التالي،

نفرض على المعاملات المشتركة بأن تكون متساوية، لذا فإن التدرج بالنسبة إلى المعاملات المشتركة سيتم جمعها في الانتشار الخلفي. على سبيل المثال، التدرج لدالة التكلفة $C(y, \bar y)$ بالنسبة إلى $u_1$ سيكون مجموع تدرج دالة التكلفة $C(y, \bar y)$ بالنسبة لـ $w_1$ وتدرج دالة التكلفة $C(y, \bar y)$ بالنسبة لـ $w_2$.

الشبكة الفائقة

الشبكة الفائقة هي شبكة يكون فيها وزن إحدى الشبكات هو ناتج شبكة أخرى. يوضح شكل 6 الرسم البياني لحساب “الشبكة الفائقة”. هنا الدالة $H$ عبارة عن شبكة ذات متجه معامل $u$ وإدخال $x$. نتيجة لذلك، يتم تكوين أوزان $G(x,w)$ ديناميكيًا بواسطة الشبكة $H(x,u)$. على الرغم من أن هذه فكرة قديمة، إلا أنها تظل قوية للغاية.

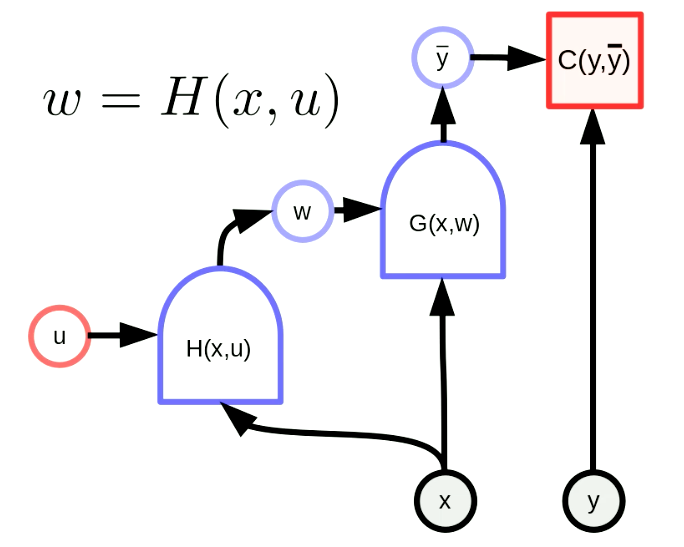
شكل 6 الشبكات الفائقة

اكتشاف العناصر الرئيسية في البيانات المتسلسلة

يمكن تطبيق تحويل مشاركة الوزن لاكتشاف العناصر الرئيسية في البيانات (motif detection). يعني اكتشاف العناصر الرئيسية العثور على بعض الأشكال في البيانات المتسلسلة مثل الكلمات الرئيسية في الكلام أو النص. تتمثل إحدى طرق تحقيق ذلك، كما هو موضح في شكل 7، في استخدام نافذة منزلقة على البيانات، والتي تنقل وظيفة مشاركة الوزن لاكتشاف فكرة معينة (أي صوت معين في إشارة الكلام) ، ويتم توجيه المخرجات (أي النتيجة) إلى دالة قصوى.

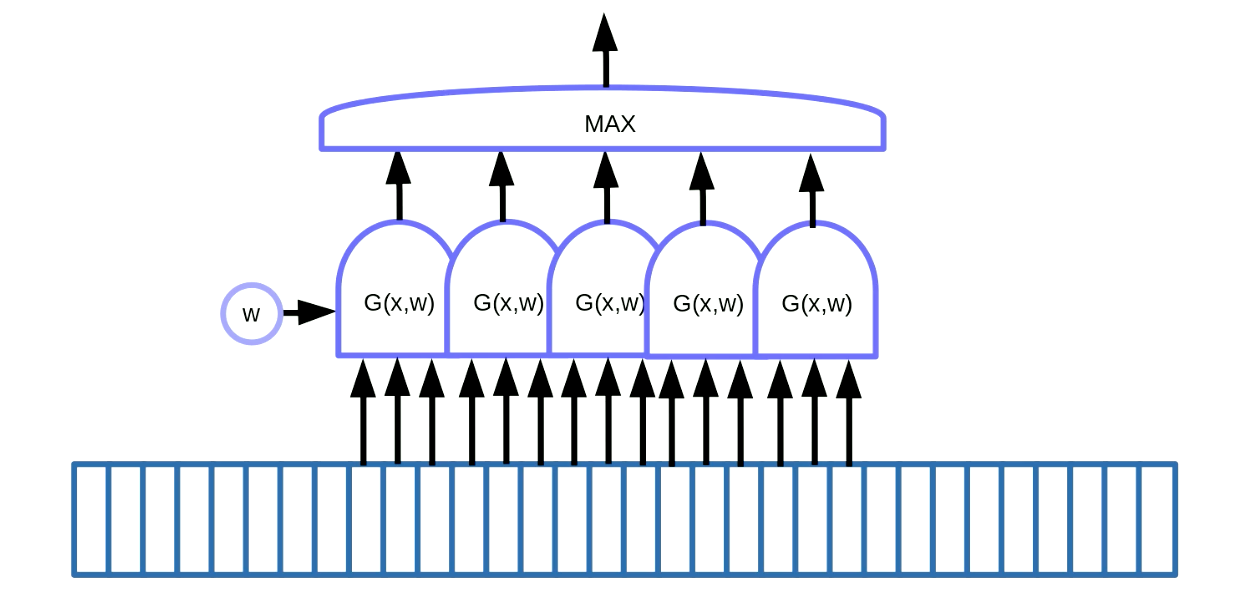
شكل 7 اكتشاف العناصر الرئيسية في البيانات المتسلسلة

في هذا المثال لدينا 5 من هذه الدوال. كنتيجة لهذا الحل، نلخص خمسة تدرجات ونعيد نشر الخطأ لتحديث المعامل $w$. عند تنفيذ هذا في PyTorch، يجب أن نمنع التراكم الضمني لهذه التدرجات، لذلك نحتاج إلى استخدام zero_grad() لتهيئة التدرج.

اكتشاف العناصر الرئيسية في الصور

التطبيق المفيد الآخر هو اكتشاف العناصر الرئيسية في الصور. عادةً ما نقوم بتمرير “القوالب” الخاصة بنا فوق الصور لاكتشاف الأشكال المستقلة عن الموقع وتشوه الأشكال. مثال بسيط هو التمييز بين “C” و”D” ، كما هو موضح في شكل 8. الفرق بين “C” و “D” هو أن “C” لها نقطتا نهاية و”D” لها ركنان. إذًا، يمكننا تصميم “قوالب نقطة النهاية” و “قوالب الزاوية”. إذا كان الشكل مشابهًا لـ “القوالب” ، فسيكون له مخرجات قيمتها تتجاوز الحد الأدنى. ثم يمكننا تمييز الحروف من هذه المخرجات عن طريق جمعها. في شكل 8، تكتشف الشبكة نقطتي نهاية، ولا ترى أي زوايا، لذلك تقوم بتنشيط “C”.

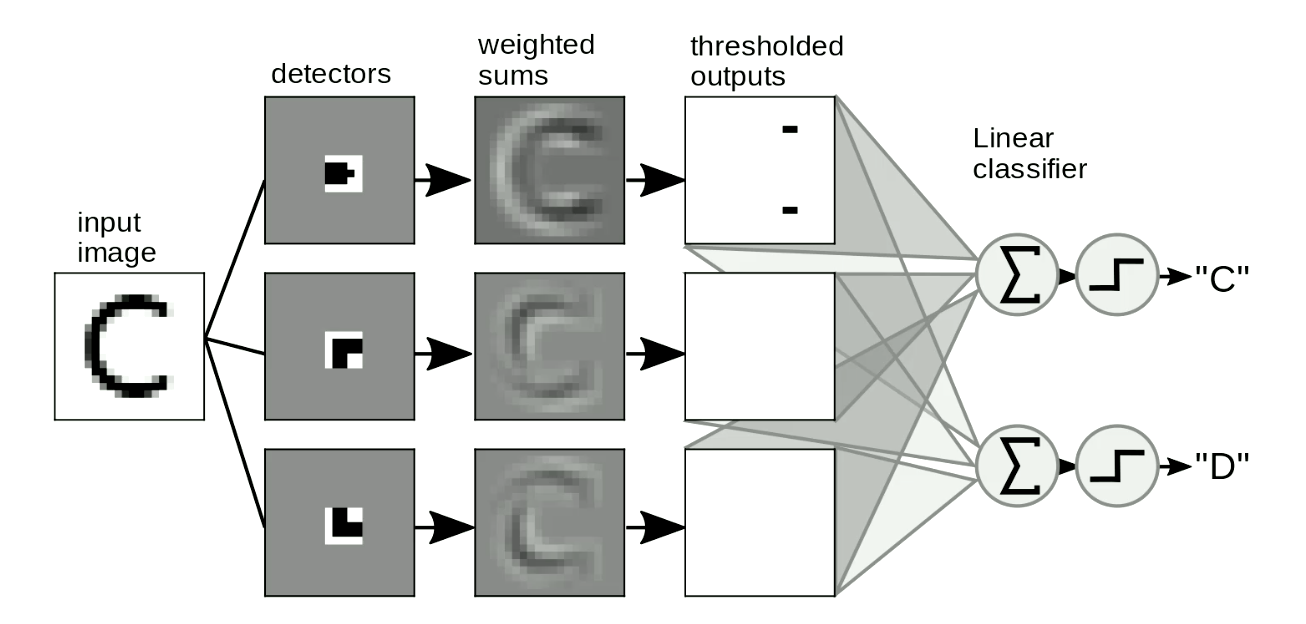
شكل 8 الكشف عن العناصر الرئيسية في الصور

من المهم أيضًا أن تكون “عملية مطابقة القالب” الخاصة بنا لا تتأثر بالتحول - عندما نزيح المدخلات، يجب ألا يتغير الناتج (أي الحرف المكتشف). يمكن حل هذا من خلال تحويل مشاركة الأوزان. كما يوضح شكل 9، عندما نغير موقع “D”، لا يزال بإمكاننا اكتشاف أشكال الزوايا حتى وإن تم إزاحتها. عندما بجمع العناصر الرئيسية (motifs)، سيتم تنشيط اكتشاف “D”.

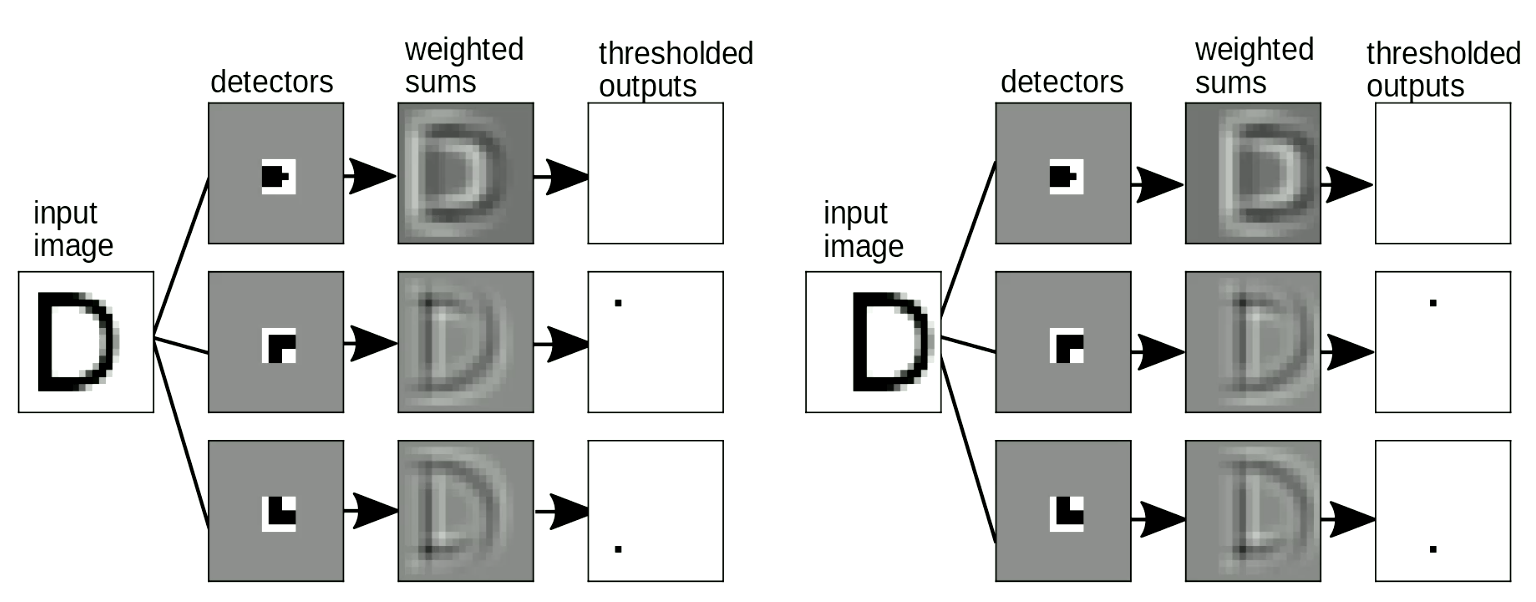
شكل 9 مقاومة الإزاحة

تم استخدام هذه الطريقة المصنوعة يدويًا لاستخدام أجهزة الكشف المحلية والتجميع للتعرف على الأرقام لسنوات عديدة. لكنها تمثل لنا المشكلة التالية: كيف يمكننا تصميم هذه “القوالب” تلقائيًا؟ هل يمكننا استخدام الشبكات العصبية لتعلم هذه “القوالب”؟ بعد ذلك ، سوف نقدم مفهوم الالتفافات ، أي العملية التي نستخدمها لمطابقة الصور مع “القوالب”.

الالتفاف المتقطعة

الالتفاف

التعريف الرياضي الدقيق للالتفاف في الحالة أحادية البعد بين المدخلات $x$ و $w$ هو:

كلاميًا، يُحسب العنصر رقم $i$ من المخرجات كحاصل الضرب النقطي بين معكوس $w$ ونافذة من نفس الحجم في $x$. لحساب الناتج كاملًا، ابدأ بالنافذة من البداية، وانقل هذه النافذة بمقدار عنصر واحد في كل مرة وكرر العملية حتى يتم استنفاد $x$.

الارتباط المتبادل

من الناحية العملية، تختلف المنهجية المعتمدة في أطر التعلم العميق مثل PyTorch قليلاً. يتم تنفيذ الالتفاف في PyTorch حيث لا يتم عكس $w$:

يطلق علماء الرياضيات على هذه الصيغة اسم “الارتباط المتبادل”. في سياقنا، هذا الاختلاف هو مجرد اختلاف في الاصطلاح. عمليًا، يمكن أن يكون استخدام أي من مصطلحي الارتباط المتبادل أو التفاف إذا قرأ المرء الأوزان المخزنة في الذاكرة من الأمام أو الخلف.

إن إدراك هذا الاختلاف مهم، على سبيل المثال، عندما يرغب المرء في الاستفادة من بعض الخصائص الرياضية للالتفاف/الارتباط من النصوص الرياضية.

التفاف الأبعاد الأعلى

بالنسبة لمدخلات ثنائية الأبعاد مثل الصور، فإننا نستخدم النسخة ثنائية الأبعاد من الالتفاف:

يمكن توسيع هذا التعريف بسهولة إلى ما بعد البعدين إلى ثلاثة أو أربعة أبعاد. هنا $w$ يسمى نواة الالتفاف

التقلبات المنتظمة التي يمكن إجراؤها باستخدام العامل التلافيفي في الـ DCNN

1. توسيع الخطوات: بدلاً من إزاحة النافذة على $x$ بمقدار عنصر واحد كل مرة، يمكن للمرء القيام بذلك بخطوة أكبر (على سبيل المثال، إدخالان أو ثلاثة إدخالات في المرة الواحدة). مثال: لنفترض أن المدخل $x$ ذو بعد واحد وله حجم 100، أما $w$ فلها حجم 5. حجم المخرجات بخطوة بمقدار 1 أو 2 موضحة في الجدول أدناه:

1. الحشو: في كثير من الأحيان عند تصميم بنى الشبكات العصبية العميقة، نريد أن يكون ناتج الالتفاف بنفس حجم المدخلات. يمكن تحقيق ذلك عن طريق حشو نهايات المدخلات (عادةً) بأصفار، على كلا الجانبين عادةً. يتم إجراء الحشو في الغالب للتسهيل. يمكن أن يؤثر في بعض الأحيان على الأداء وينتج عنه تأثيرات حدودية غريبة، ومع ذلك، عند استخدام ReLU غير الخطية، فإن الحشو الصفري ليس بذاك السوء.

الشبكات العصبية الالتفافية العميقة (DCNNs)

كما وصفنا سابقًا، عادةً ما يتم تنظيم الشبكات العصبية العميقة كتناوب متكرر ما بين العوامل الخطية والطبقات اللاخطية النقطية. في الشبكات العصبية الالتفافية، سيكون العامل الخطي هو عامل الالتفاف الموصوف أعلاه. يوجد أيضًا نوع ثالث اختياري من الطبقات يسمى طبقة التجميع (pooling layer).

السبب في تكديس العديد من هذه الطبقات هو أننا نريد بناء تمثيل هرمي للبيانات. لا يجب أن تقتصر شبكات CNN على معالجة الصور، فقد تم تطبيقها بنجاح على الكلام واللغة. من الناحية الفنية، يمكن تطبيقها على أي نوع من البيانات التي تأتي في شكل مصفوفات، طالما أنها تحقق خصائص معينة.

لماذا نريد التقاط التمثيل الهرمي للعالم؟ لأن العالم الذي نعيش فيه مركب. تمت الإشارة إلى هذه النقطة في الأقسام السابقة. يمكن ملاحظة هذه الطبيعة الهرمية من حقيقة أن البيكسلات المحلية تتجمع لتشكيل أشكال بسيطة مثل الحواف الموجهة. يتم تجميع هذه الحواف بدورها لتشكيل سمات محلية مثل الزوايا والوصلات على شكل حرف T وما إلى ذلك. يتم تجميع هذه الحواف لتشكيل أشكال أكثر تجريدًا. يمكننا الاستمرار في البناء على هذا التمثيل الهرمي نهايةً لتشكيل الأشياء التي نلاحظها في العالم الحقيقي.

شكل 10 تصور ميزة الشبكة الالتفافية المدربة على ImageNet من [Zeiler & Fergus 2013]

إن هذه الطبيعة الهرمية التركيبية التي نلاحظها في العالم الطبيعي ليست نتيجة إدراكنا البصري فحسب، بل هي أيضًا حقيقية على المستوى المادي. في أدنى مستوى من الوصف، لدينا جسيمات أولية، تتجمع لتكوين ذرات، وتشكل الذرات معًا جزيئات، ونستمر في البناء على هذه العملية لتشكيل المواد، وأجزاء من الكائنات، وفي النهاية كائنات كاملة في العالم المادي.

قد تكون الطبيعة التركيبية للعالم هي الإجابة على سؤال أينشتاين البلاغي حول كيفية فهم البشر للعالم الذي يعيشون فيه:

أكثر ما لا يمكن فهمه في الكون هو أنه يمكن فهمه.

حقيقة أن البشر يفهمون العالم بفضل هذه الطبيعة التركيبية لا تزال تبدو وكأنها مؤامرة بالنسبة لـ Yann. ومع ذلك، يقال إنه بدون التكوين، سوف يتطلب الأمر المزيد من السحر حتى يفهم البشر العالم الذي يعيشون فيه. نقلاً عن عالم الرياضيات العظيم ستيوارت جيمان:

العالم مؤلف أو الله موجود.

إلهام من علم الأحياء

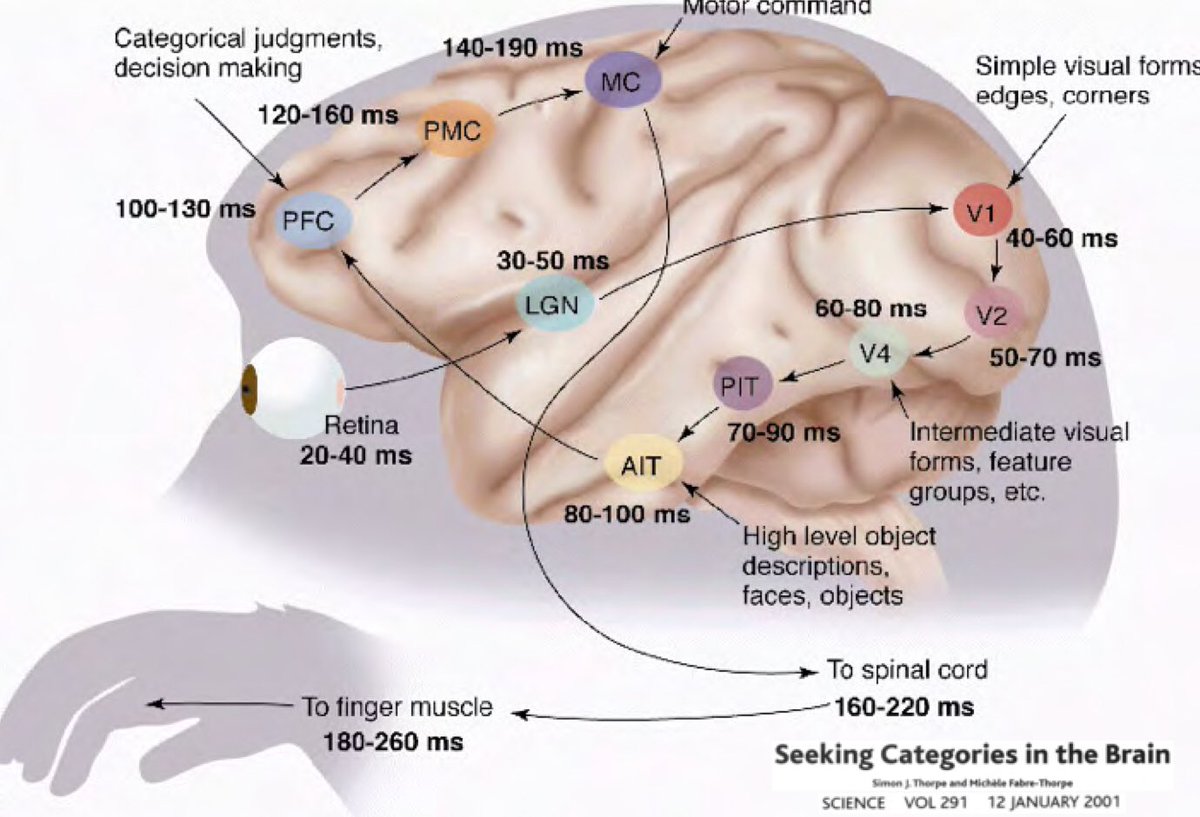
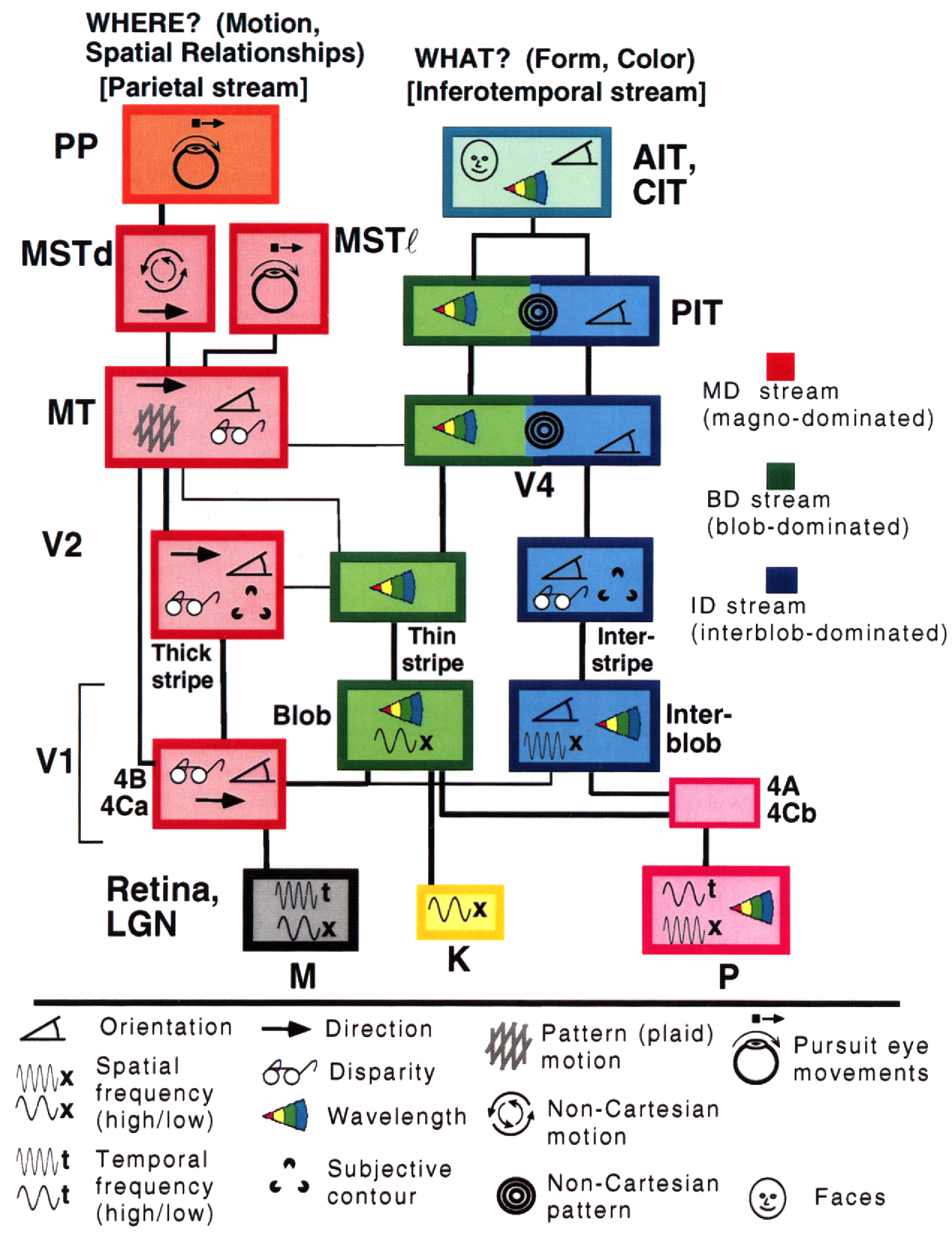
إذًا، لماذا يجب أن يتأصل التعلم العميق في فكرة أن عالمنا مفهوم وله طبيعة تركيبية؟ ساعد البحث الذي أجراه Simon Thorpe في تحفيز هذا الأمر بشكل أكبر. أظهر أن الطريقة التي نتعرف بها على الأشياء اليومية سريعة للغاية. تضمنت تجاربه وميض مجموعة من الصور كل 100 مللي ثانية، ثم يطلب من المستخدمين تحديد هذه الصور، وهو ما تمكنوا من القيام به بنجاح. أظهر هذا أن الأمر يستغرق حوالي 100 مللي ثانية بالنسبة للبشر لاكتشاف الأشياء. علاوة على ذلك، ضع في اعتبارك الرسم التخطيطي أدناه، والذي يوضح أجزاء من الدماغ مشروحة بالوقت الذي تستغرقه الخلايا العصبية للانتشار من منطقة إلى أخرى:

شكل 11 نموذج سايمون ثورب لتدفق المعلومات المرئية في الدماغ

تنتقل الإشارات من شبكية العين إلى الـ LGN (تساعد في تحسين التباين، والتحكم في البوابة، وما إلى ذلك) ، ثم إلى القشرة البصرية الأولية V1، وV2، وV4، ثم إلى القشرة الباطنية الصدغية (PIT) ، وهي جزء من الدماغ حيث يتم تعريف الفئات أو الأصناف. أظهرت الملاحظات من جراحة الدماغ المفتوح أنه إذا عرضت فيلمًا على الإنسان، فإن الخلايا العصبية في الـ PIT ستطلق فقط عندما تكتشف صورًا معينة - مثل جينيفر أنيستون أو جدة شخص ما - ولا شيء آخر. الاشتعالات العصبية لا تتأثر بأمور كالموضع والحجم والإضاءة واتجاه جدتك وما ترتديه وما إلى ذلك. علاوة على ذلك، فإن أوقات رد الفعل السريعة التي تمكن البشر من تصنيف هذه العناصر - وقت لا يكاد يسمح إلا بانتقال بضع إشارات - توضح أنه من الممكن القيام بذلك دون قضاء وقت إضافي في العمليات الحسابية المتكررة المعقدة. بدلا من ذلك، هذه عملية تغذية أمامية واحدة. تقترح هذه الأفكار أنه يمكننا تطوير بنية شبكة عصبية تكون متطورة تمامًا، ومع ذلك لا تزال قادرة على حل مشكلة التعرف، بطريقة لا تتأثر بالتحولات التي لا علاقة لها بالمدخلات. هناك منطور أخرى للدماغ البشري من Gallant وVan Essen، اللذين يوضح نموذجهما للدماغ البشري مسارين متميزين:

شكل 12 نموذج Gallen وVan Essen للممرات الظهرية والبطنية في الدماغ

يُظهر الجانب الأيمن المسار البطني، الذي يخبرك بما تنظر إليه، بينما يُظهر الجانب الأيسر المسار الظهري، والذي يحدد المواقع والهندسة والحركة. يبدو أنها منفصلة إلى حد ما عند الإنسان (والثديات) في القشرة البصرية (مع وجود بعض التفاعلات بينهما بالطبع). ### مساهمات Hubel و Weisel (1962)

شكل 13 تجارب Hubel و Wiesel مع المحفزات البصرية في أدمغة القطط

استخدمت تجارب Hubel و Weisel أقطابًا كهربائية لقياس الاشتعلات العصبية في أدمغة القطط استجابةً للمنبهات البصرية. اكتشفوا أن الخلايا العصبية في منطقة V1 حساسة فقط لمناطق معينة من المجال البصري (تسمى "المجالات المستقبلة")، وتكتشف الحواف الموجهة في تلك المنطقة. على سبيل المثال، أوضحوا أنه إذا عرضت على القط شريطًا رأسيًا وبدأت في تدويره، عند زاوية معينة سيتم تحفيز خلية عصبية. وبالمثل، عندما يتحرك الشريط بعيدًا عن تلك الزاوية، يتضاءل ذاك الاشتعال في تلك الخلية. أطلق Hubel و Weisel على هذه الخلايا العصبية الانتقائية للتنشيط اسم "الخلايا البسيطة"، لقدرتها على اكتشاف السمات المحلية. اكتشفوا أيضًا أنه إذا قمت بتحريك الشريط خارج المجال الاستقبالي، فإن تلك الخلية العصبية تتوقف عن الاشتعال تمامًا، ولكن خلية عصبية أخرى ستنطلق. هناك كواشف لخصائص محلية تتوافق مع جميع مناطق المجال البصري، ومن هنا جاءت فكرة أن الدماغ البشري يعالج المعلومات المرئية كمجموعة من "الالتفافات". نوع آخر من الخلايا العصبية، أطلقوا عليه اسم "الخلايا المعقدة"، يجمع ناتج خلايا بسيطة متعددة في منطقة معينة. يمكننا التفكير في تلك الخلايا على أنها تحسب إجمالي عمليات التنشيط باستخدام دوال مثل الحد الأقصى (maximum) أو المجموع (sum) أو مجموع المربعات (sum of squares) أو أي وظيفة أخرى لا تعتمد على الترتيب. تكتشف هذه الخلايا المعقدة الحواف والتوجهات في منطقة ما، بغض النظر عن مكان تواجد هذه المحفزات داخل المنطقة تحديدًا. بمعنى آخر، فهي مقاومة للإزاحة فيما بالنسبة للاختلافات الصغيرة في مواقع المدخلات. ### مساهمات فوكوشيما (1982)

شكل 14 نموذج فوكوشيما للـ CNN

كان فوكوشيما أول من طبق فكرة الطبقات المتعددة من الخلايا البسيطة والخلايا المعقدة بنماذج الكمبيوتر، باستخدام مجموعة بيانات من الأرقام المكتوبة بخط اليد. تم تصميم بعض أجهزة الكشف عن الميزات هذه يدويًا أو بالتعلم، على الرغم من أن التعلم استخدم خوارزميات تجميع بدون إشراف، تم تدريبها بشكل منفصل لكل طبقة، حيث لم يتم استخدام الانتشار الخلفي بعد. جاء Yann LeCun بعد بضع سنوات (1989، 1998) ونفذ نفس الهيكل، لكن هذه المرة دربهم في بيئة خاضعة للإشراف باستخدام الانتشار الخلفي. يُنظر إلى هذا على نطاق واسع على أنه نشأة الشبكات العصبية الالتفافية الحديثة. (ملاحظة: في عام 1999 أعاد Riesenhuber من MIT اكتشاف هذه البنية أيضًا، ولكن لم يستخدم الانتشار الخلفي).