الشبكات العصبية الاصطناعية (ANNs)
🎙️ Alfredo Canzianiالتعلم بالإشراف للتصنيف
-
لنأخذ في عين الاعتبار الشكل 1 (أ) أدناه. تقع النقاط في هذا الرسم البياني على فروع اللولب، في $\R^2$. يمثل كل لون تسمية لفئة أو فصيلة. عدد الفئات الفريدة هو $K = 3$. يتم تمثيل هذا رياضياً بواسطة معادلة 1 (أ).
-
شكل 1 (ب) يُظهر لولبًا مشابهًا، مع اضافة عنصر التشويش الغاوسي (Gaussian noise). يتم تمثيل هذا رياضياً بواسطة معادلة 1 (ب).
في كلتا الحالتين، لا يمكن فصل هذه النقاط خطيًا.
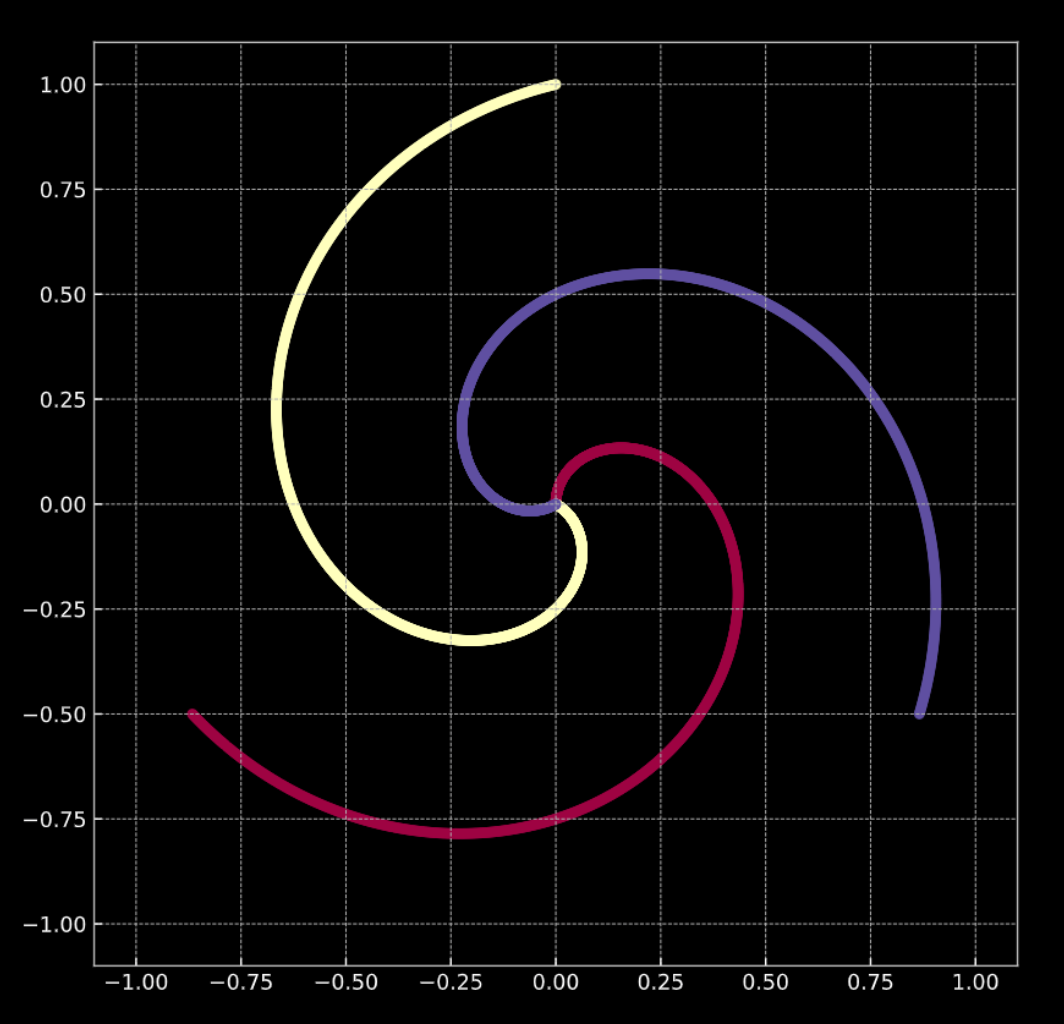
الشكل 1(أ) لولب "نظيف" ثنائي الأبعاد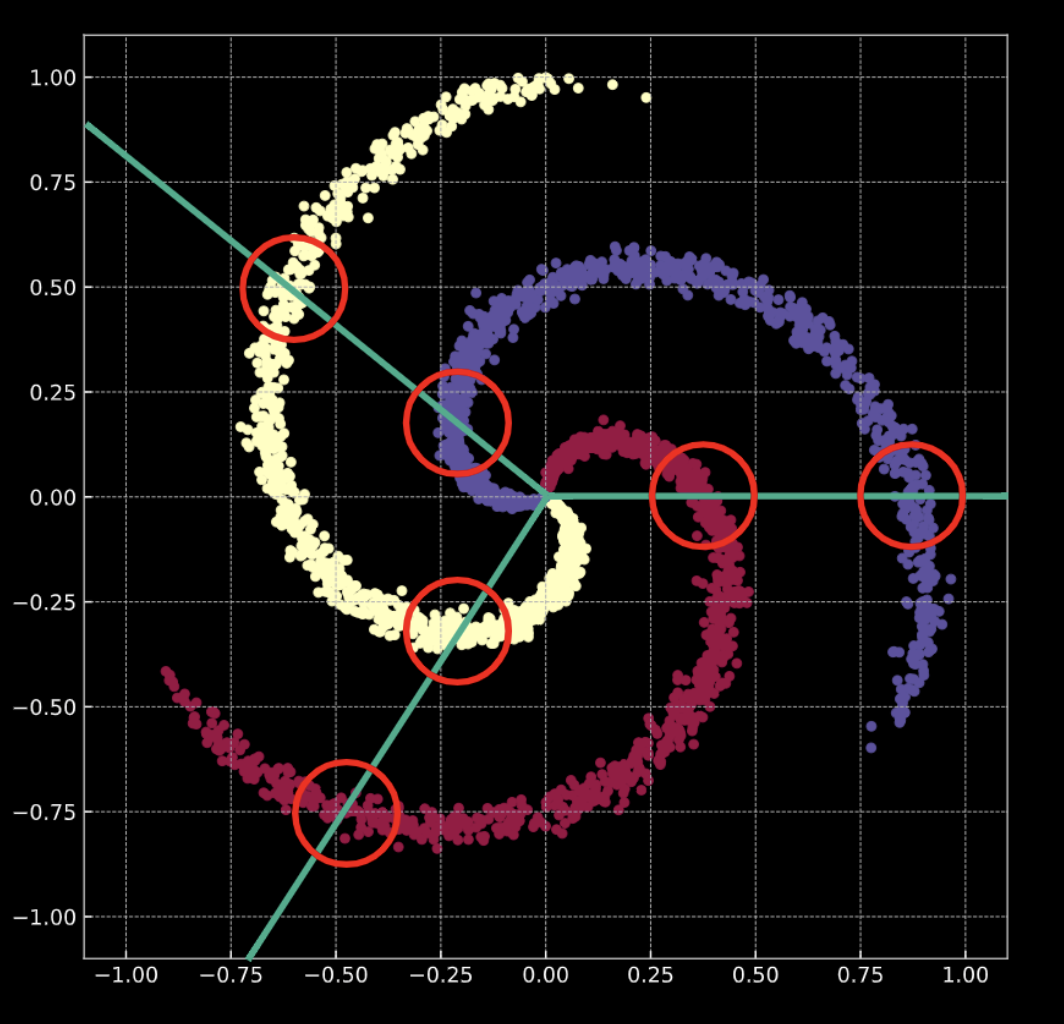
الشكل 1(ب) لولب "مشوش" ثنائي الأبعاد
ماذا يعني القيام بالتصنيف؟ خذ بعين الاعتبار حالة الانحدار اللوجستي. إذا تم تطبيق الانحدار اللوجستي للتصنيف على هذه البيانات، فسيؤدي ذلك إلى إنشاء مجموعة من المستويات الخطية (حدود القرار) في محاولة لفصل البيانات إلى فئاتها. المشكلة في هذا الحل هي أنه في كل منطقة، هناك نقاط تنتمي إلى فئات متعددة. تتخطى فروع اللولب حدود القرار الخطي. هذا ليس حلاً رائعًا!
كيف نصلح ذلك؟ نقوم بتحويل مساحة المدخلات بحيث يتم إجبار البيانات على الفصل خطيًا. خلال تدريب الشبكة العصبية، ستقوم حدود القرار التي تتعلمها الشبكة بالتكيف مع توزيع بيانات التدريب.
ملاحظة: يتم دائمًا تمثيل الشبكة العصبية من أسفل إلى أعلى. الطبقة الأولى في الأسفل والأخيرة في الأعلى. هذا لأنه من الناحية النظرية، تعد المدخلات بأنها ذات خصائص منخفضة المستوى لأي مهمة تقوم بها الشبكة العصبية. عندما تنتقل البيانات لأعلى عبر الشبكة، تستخرج كل طبقة لاحقة خصائصًا على مستوى أعلى.
بيانات التدريب
في الأسبوع الماضي، رأينا أن الشبكة العصبية التي يتم تهيئتها حديثًا تحول مدخلاتها بطريقة عشوائية. ومع ذلك، فإن هذا التحول غير مفيد (في البداية) في أداء المهمة المرادة. سنكتشف كيف يمكننا باستخدام البيانات إجبار هذا التحول على الحصول على بعض المعاني ذات الصلة بالمهمة قيد البحث. فيما يلي، تجدون البيانات المستخدمة كمدخل لتدريب الشبكة.
- يمثل $\vect{X}$ بيانات المدخلات وهي مصفوفة بأبعاد $m$ (عدد نقاط بيانات التدريب) $times$ $n$ (أبعاد كل نقطة إدخال). في حالة البيانات الموضحة في الأشكال 1 (أ) و 1 (ب)، $n = 2$.
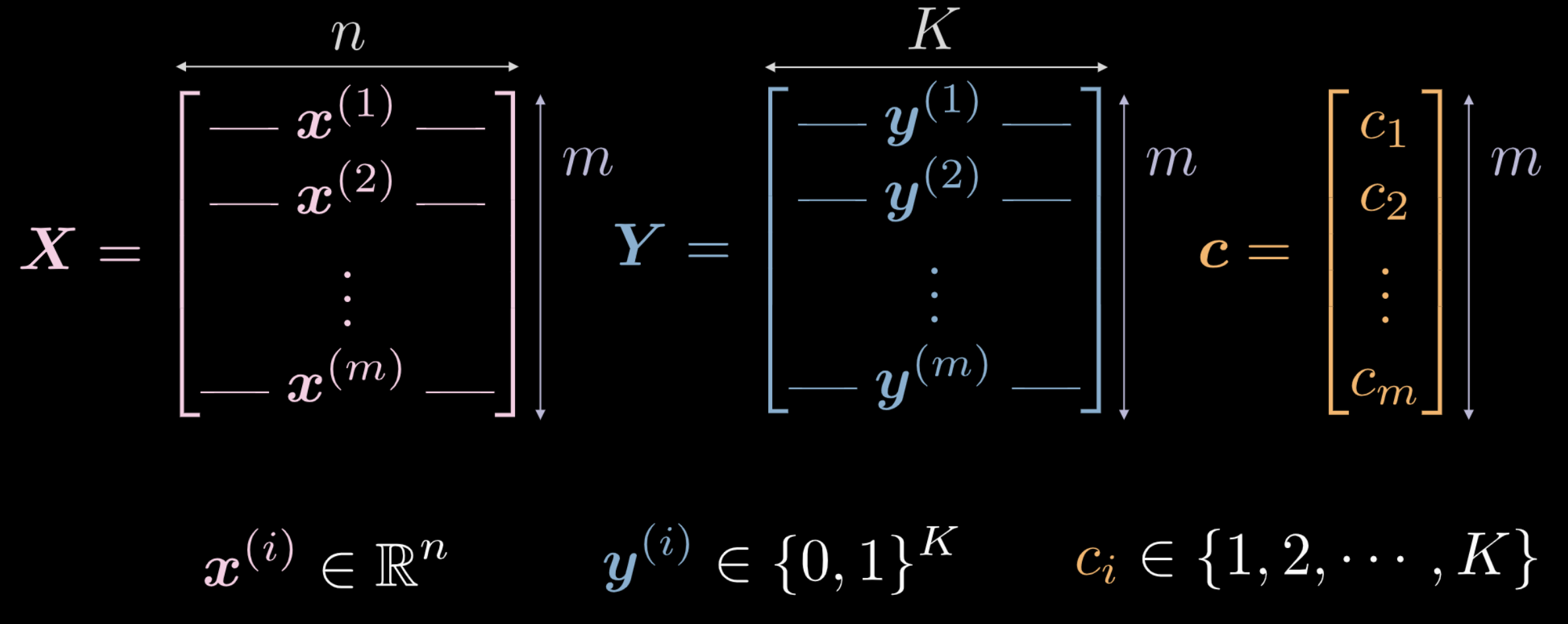
شكل 2 بيانات التدريب
-
يمثل كل من متجه $\vect{c}$ ومصفوفة $\boldsymbol{Y}$ مسميات فئة كل نقطة من نقاط البيانات $m$. في المثال أعلاه، هناك 3 فئات مختلفة.
- $c_i \in \lbrace 1, 2, \cdots, K \rbrace$، و $\vect{c} \in \R^m$. ومع ذلك، قد لا نستخدم $\vect{c}$ كبيانات تدريب. إذا استخدمنا مسميات رقمية للفئات المختلفة $c_i \in \lbrace 1, 2, \cdots, K \rbrace$، فقد تستنتج الشبكة ترتيبًا داخليًا للفئات لا علاقة له بتوزيع البيانات.
- لتجاوز هذه المشكلة، نستخدم ترميز فعال ذو بت واحد (one-hot encoding). لكل فئة $c_i$، يتم إنشاء متجه صفري ببعد $K$ والمعرف كـ $\vect{y}^{(i)}$، والذي يكون عنصره الـ $c_i$ مضبوطًا على $1$ (انظر شكل 3 أدناه).

شكل 3 ترميز فعال ذو بت واحد (one-hot encoding)
- لذلك ، $\boldsymbol Y \in \R^{m \times K}$. يمكن أيضًا اعتبار هذه المصفوفة على أنها تحتوي على بعض الكتلة الاحتمالية، والتي تتركز بشكل كامل على إحدى نقاط $K$.
الطبقات المتصلة بالكامل (FC)
سنلقي الآن نظرة على ماهية الشبكة المتصلة بالكامل (FC) وكيفية عملها.
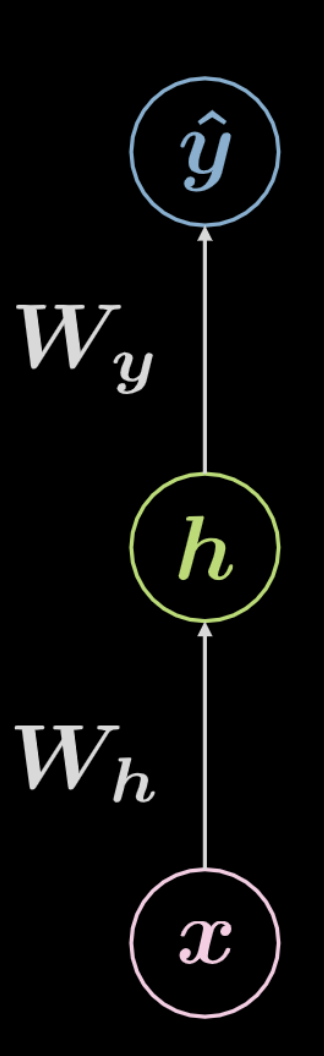
شكل 4 شبكة عصبية متصلة بالكامل
لنأخذ بعين الاعتبار الشبكة الموضحة أعلاه في الشكل 4. تخضع المدخلات، $\boldsymbol x$، لتحويل تآلفي (affine transformation) معرف بواسطة $\boldsymbol W_h$، متبوعًا بتحويل غير خطي. يُشار إلى نتيجة هذا التحويل غير الخطي بـ $\boldsymbol h$، والتي تمثل ناتجًا خفيًا ، أي ناتج غير مرئي من خارج الشبكة. يتبع ذلك تحول تآلفي آخر ($\boldsymbol W_y$)، متبوعًا بتحويل غير خطي آخر. ينتج عن هذا الناتج النهائي $\boldsymbol{\hat{y}}$. يمكن تمثيل هذه الشبكة رياضياً بواسطة المعادلات في معادلة 2 أدناه. $f$ و$g$ كلاهما غير خطيين.
\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\]الشبكة العصبية الأساسية مثل الشبكة الموضحة أعلاه هي مجرد مجموعة من الأزواج المتتالية، حيث يكون كل زوج عبارة عن تحويل تآلفي متبوعًا بعملية غير خطية (عملية سحق). تتضمن الوظائف غير الخطية المستخدمة بشكل متكرر الآتي: ReLU ، السيني (sigmoid)، الظل الزائدي (hyperbolic tangent)، وsoftmax.
الشبكة الموضحة أعلاه عبارة عن شبكة ثلاثية الطبقات:
- مدخلات الخلايا العصبية
- الخلايا العصبية الخفية
- مخرجات الخلايا العصبية
لذلك، تحتوي الشبكة العصبية المكونة من $3$ طبقات على اثنين من التحولات التآلفية. يمكن أن يمتد هذا إلى شبكة لها $n$ من الطبقات.
الآن دعونا ننتقل إلى حالة أكثر تعقيدًا.
لندرس حالة مكونة من 3 طبقات خفية، ومتصلة بالكامل في كل طبقة. يمكن العثور على رسم توضيحي في شكل 5
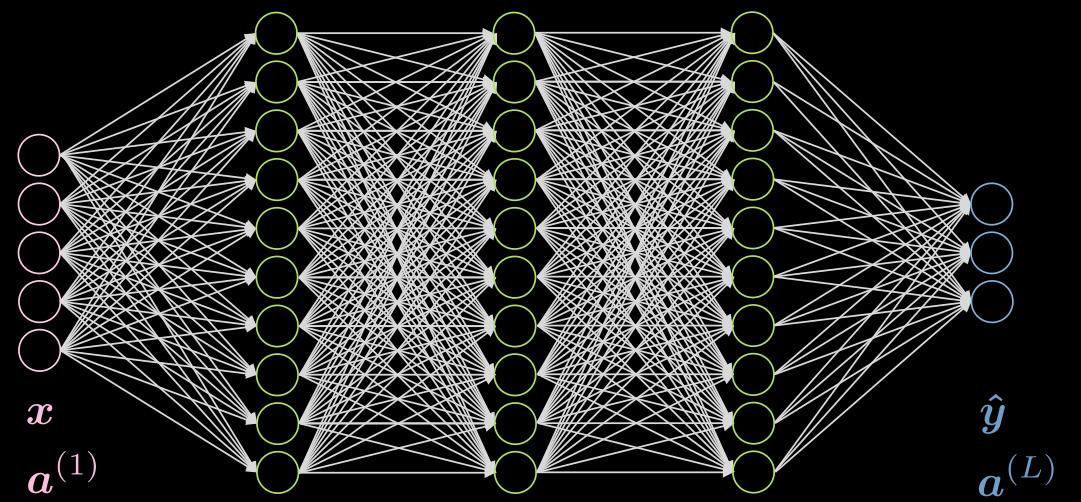
شكل 5 شبكة عصبية بثلاث طبقات مخفية
لنأخذ في عين الاعتبار خلية عصبية $j$ في الطبقة الثانية. التنشيط لها هو:
\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]حيث $\vect{w}^{(j)}$ هو الصف رقم $j$ من $\vect{W}^{(1)}$.
لاحظ أن تنشيط طبقة المدخلات في هذه الحالة هو مجرد مصفوفة الوحدة. يمكن أن تحتوي الطبقات المخفية على عمليات تنشيط مثل ReLU، الظل الزائدي (hyperbolic tangent)، السيني (sigmoid)، soft (arg)max ، إلخ.
سيعتمد تنشيط الطبقة الأخيرة بشكل عام على التطبيق الخاص بك، كما هو موضح في هذا المنشور على Piazza.
الشبكة العصبية (التنبؤ)
دعنا نفكر في الشبكة العصبية ثلاثية الطبقات مرة أخرى (المدخلات والطبقة الخفية والمخرجات)، كما هو موضح في الشكل 6
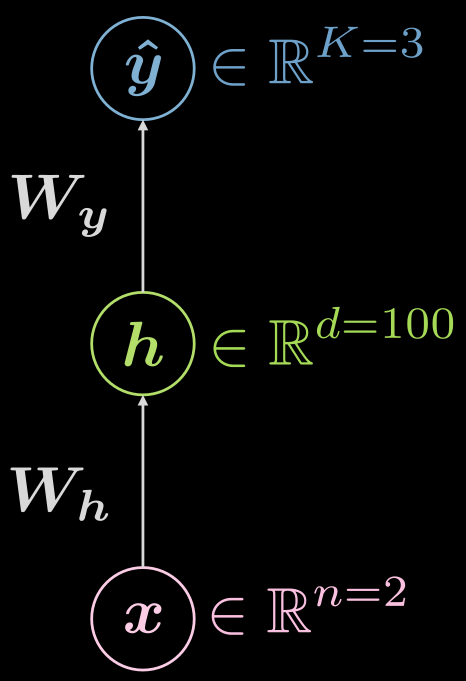
شكل 6 شبكة عصبية ثلاثية الطبقات
ما نوع الوظائف التي نبحث عنها؟
\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]ومع ذلك، من المفيد تصور حقيقة وجود طبقة مخفية، ويمكن توسيع التعيين على النحو التالي:
\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]كيف يمكن أن يبدو نموذج التكوين للحالة أعلاه؟ في هذه الحالة، يكون لدى المرء مدخلات من البعد الثاني ($n=2$) ، ويمكن أن يكون للطبقة المخفية الفردية أبعاد بمقدار 1000 ($d = 1000$) ، ولدينا 3 فئات ($C=3$). هناك أسباب عملية جيدة لعدم وجود الكثير من الخلايا العصبية في طبقة مخفية واحدة ، لذلك قد يكون من المنطقي تقسيم الطبقة المخفية الواحدة إلى 3 طبقات تحتوي كل منها على 10 خلايا عصبية ($1000 \rightarrow 10 \times 10 \times 10$)
الشبكة العصبية (التدريب الأول)
إذن كيف يبدو التدريب النموذجي؟ من المفيد صياغة ذلك باستخدام المصطلحات المتعارف عليها للخسائر.
أولاً، دعنا نعيد تقديم soft (arg)max ونشير صراحةً إلى أنها دالة تنشيط شائعة للطبقة الأخيرة، عند استخدام خسارة الأرجحية اللوغاريثمية السلبية (negative log-likelihood loss)، في حالات التنبؤ متعدد الفئات. كما ذكر البروفيسور لوكان (LeCun) في المحاضرة، هذا لأنك تحصل على تدرجات أفضل مما لو كنت تستخدم sigmoids وفقدان المربع (square loss). بالإضافة إلى ذلك، ستكون طبقتك الآخير قد سبق تسويها (مجموع كل الخلايا العصبية في الطبقة الأخيرة يساوي 1)، وهذا أفضل لطرق التدرج من التسوية الصريحة (بالقسمة على المعيار norm).
سوف يعطيك soft (arg)max عدد من الـ logits في الطبقة الأخيرة التي تبدو كما يلي:
\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]من المهم ملاحظة أن المجموعة ليست مغلقة بسبب إيجابية الدالة الأسية.
بالنظر إلى مجموعة التوقعات $\matr{\hat{Y}}$، ستكون الخسارة:
\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]هنا يشير $c$ إلى تسمية العدد الصحيح، وليس تمثيلاً بالترميز ذو بت واحد.
لذلك دعونا نقوم بطرح مثالين، أحدهما يتم فيه تصنيف المثال بشكل صحيح، وأما الآخر فلا.
لنقول
\[\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\]ما هو مقدار الخسارة لكل مثال؟
في حالة التنبؤ شبه المثالي ($\sim$ يعني حوالي):
\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\ \sim 0 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow 0^{+}\]في حالة التنبؤ الخاطئ تمامًا تقريبًا:
\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\ \sim 1 \\ \sim 0 \end{pmatrix}} , 1\right) \rightarrow +\infty\]لاحظ في الأمثلة أعلاه، $\sim 0 \rightarrow 0^{+}$ و $\sim 1 \rightarrow 1^{-}$. لماذا هو كذلك؟ خذ دقيقة للتفكير.
ملاحظة: من المهم أن تعرف أنه إذا كنت تستخدم CrossEntropyLoss، فستحصل على LogSoftMax وأرجحية لوغاريثمية سلبية NLLLoss مجتمعة معًا، لذا لا تفعل ذلك مرتين!
الشبكة العصبية (التدريب الثاني)
للتدريب، نقوم بتجميع جميع المعاملات القابلة للتدريب - مصفوفات الأوزان والتحيزات - في مجموعة نسميها $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$. هذا يسمح لنا بكتابة دالة الهدف أو الخسارة على النحو التالي:
\[J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}} \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]هذا يجعل الخسارة تعتمد على ناتج الشبكة $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$، لذا يمكننا تحويل هذا إلى مشكلة تحسين.
يمكن رؤية توضيح بسيط لكيفية عمل ذلك في الشكل 7، حيث $J(\vartheta)$، وهي الدالة التي نحتاج إلى تصغيرها، ولها فقط معامل عددي $\vartheta$.
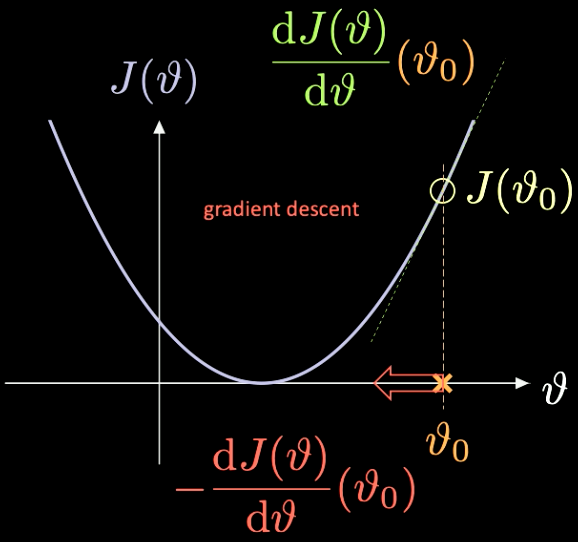
شكل 7 تحسين دالة الخسارة من خلال الانحدار التدرجي.
نختار نقطة تهيئة عشوائية $\vartheta_0$ - مع الخسارة المرتبطة بها $J(\vartheta_0)$. يمكننا حساب المشتقة عند تلك الننقطة $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$. في تلك الحالة، يصبح ميل المشتقة موجبًا. لذلك نحن بحاجة إلى اتخاذ خطوة في اتجاه أقصى انحدار. في هذه الحالة الاتجاه هو $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$.
تُعرف الإعادة التكرارية لهذه العملية بالانحدار التدرجي. طرق التدرج هي الأدوات الأساسية لتدريب الشبكة العصبية.
من أجل حساب التدرجات اللازمة، علينا استخدام الانتشار الخلفي
\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]التصنيف اللولبي - Jupyter مذكرة
يمكن العثور على مذكرة Jupyter هنا. لتشغيل المذكرة، تأكد من تثبيت بيئة the dl-minicourse كما هو موضح في README.md.
يمكن العثور على شرح لكيفية استخدام torch.device() في ملاحظات الأسبوع الماضي.
كما في السابق، سنعمل مع النقاط في $\mathbb{R}^2$ بثلاث تسميات لفئات مختلفة - باللون الأحمر والأصفر والأزرق - كما هو موضح في شكل 8.

شكل 8 بيانات التصنيف اللولبي.
nn.Sequential() هو عبارة عن حاوية (container)، تمرر الوحدات إلى المُنشئ (constructor) بالترتيب الذي تم إضافتها إليها. مسمى nn.linear() هو تسمية غير مطابقة للوظيفة حيث أنه يسخدم لتطبيق تحويل تآلفي (affine) على البيانات الواردة: $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$. لمزيد من المعلومات، راجع PyTorch وثائق.
تذكر أن التحول التآلفي يشمل خمسة تحولات: الدوران، والانعكاس، التحريك، التحجيم، والقص (shearing).
كما يمكن رؤيته في شكل 9، عند محاولة فصل البيانات اللولبية بحدود القرار الخطية - فقط باستخدام وحدات nn.linear()، دون وجود دوال لاخطية بينها - أفضل ما يمكننا تحقيقه هو دقة تصل إلى $50\%$.
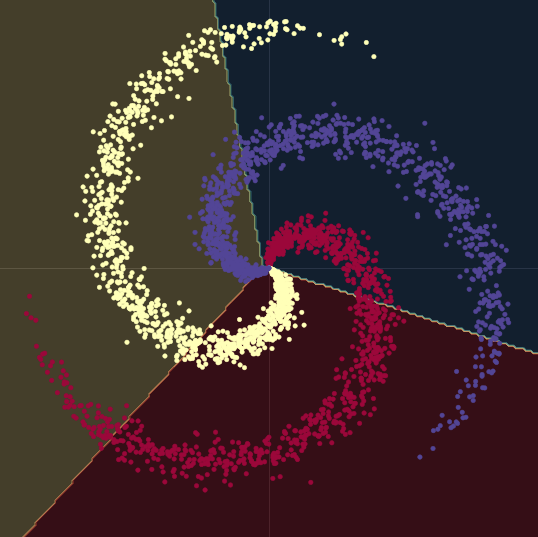
شكل 9 حدود القرار الخطية.
عندما ننتقل من نموذج خطي إلى نموذج يحتوي على وحدتين من الـ nn.linear() ويتخللها nn.ReLU()، ترتفع الدقة إلى $95\%$. هذا لأن الحدود تصبح غير خطية وتتكيف بشكل أفضل مع الشكل اللولبي للبيانات، كما يمكن رؤيته في شكل 10.
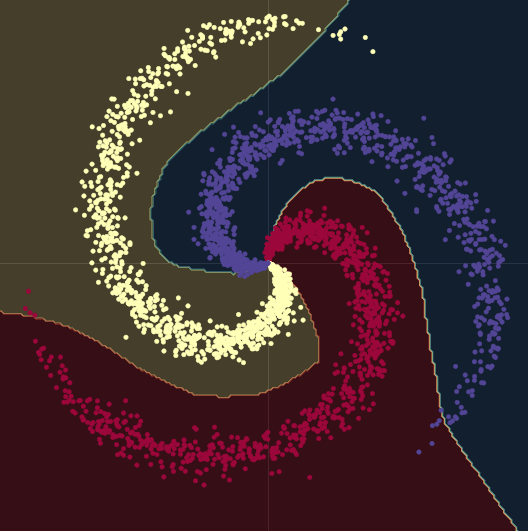
شكل 10 حدود القرار غير الخطية.
أحد الأمثلة على مشكلة الانحدار التي لا يمكن حلها بشكل صحيح باستخدام الانحدار الخطي، ولكن تُحل بسهولة باستخدام ذات بنية الشبكة العصبية يمكن إيجادها في هذه المذكرة وشكل 11، الذي يُظهر 10 شبكات مختلفة، حيث 5 منها لها دالة ربط nn.ReLU() و 5 لها nn.Tanh(). الدالة الأولى هي دالة خطية متعددة التعريف (piecewise)، في حين أن الدالة الثانية هي انحدار مستمر وسلس.
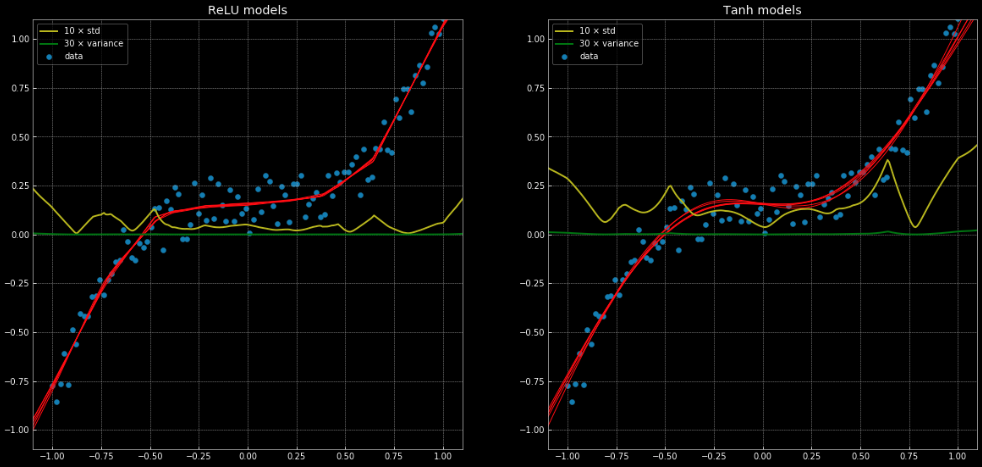
شكل 11: 10 شبكات عصبية مع تباينها وانحرافها المعياري.
اليسار: خمسة شبكات
ReLU. اليمين: خمسة شبكات tanh.
يظهر الخطان الأصفر والأخضر الانحراف المعياري والتباين للشبكات. يعد استخدام هذه العناصر مفيدًا لشيء مشابه لـ “مجال الثقة” - لأن الدوال تعطي تنبؤًا واحدًا لكل ناتج. يسمح استخدام توقع تباين المجموعة بتقدير درجة عدم اليقين بذاك التنبؤ. يمكننا ملاحظة أهمية ذلك في الشكل 12، حيث نقوم نمدد تطبيق دوال القرار خارج فترة التدريب ونلاحظ أنها تميل نحو $+\infty, -\infty$.
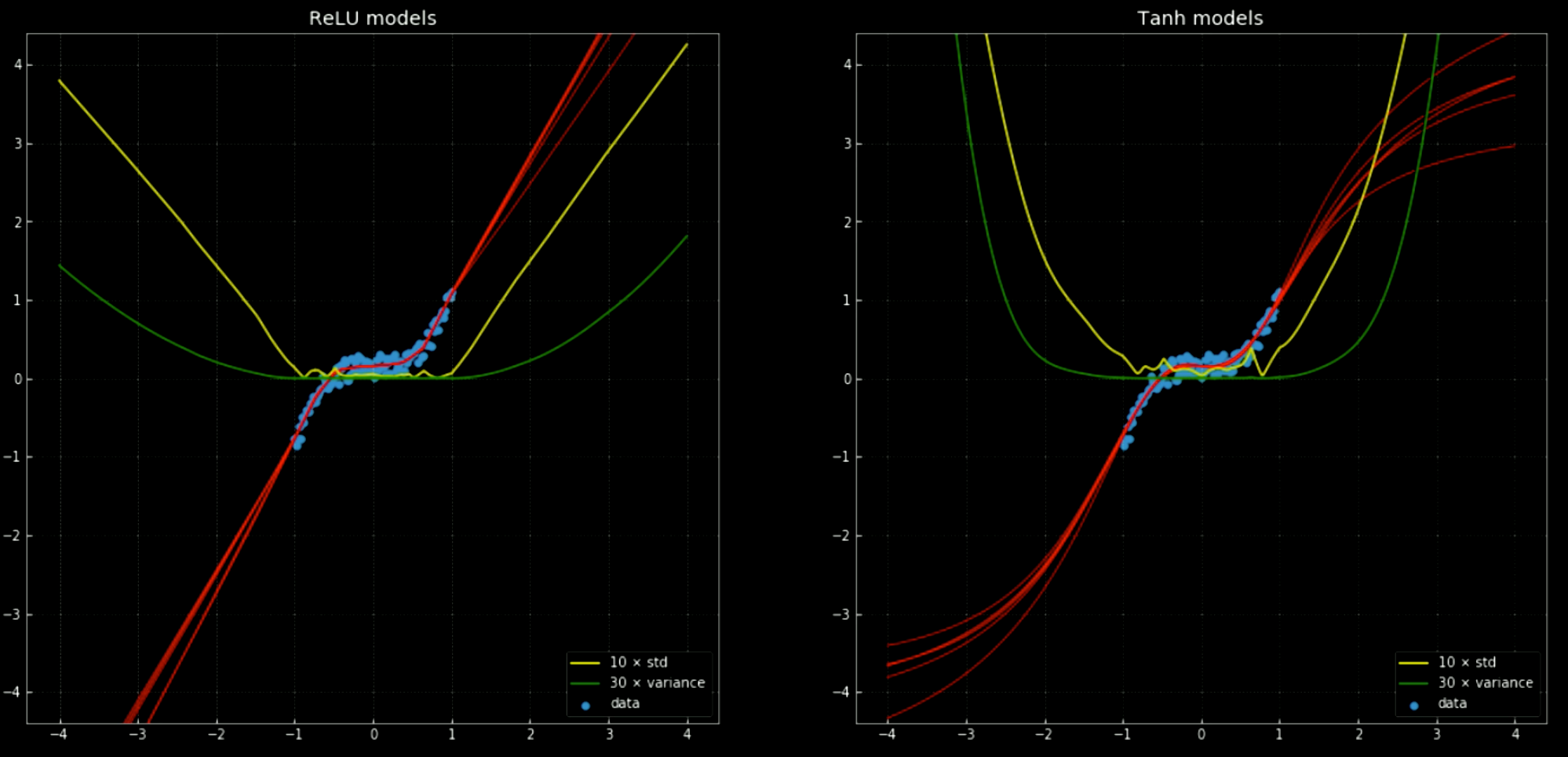
شكل 12 شبكات عصبية، مع الانحراف المعياري والمتوسط، خارج فترة التدريب.
اليسار: خمسة شبكات
ReLU. اليمين: خمسة شبكات tanh.
لتدريب أي شبكة عصبية باستخدام PyTorch، تحتاج إلى 5 خطوات أساسية في حلقة التدريب:
output = model(input)هو الممر الأمامي للنموذج، والذي يأخذ المدخلات ويولد المخرجات.J = loss(output, target <or> label)يأخذ ناتج النموذج ويحسب خسارة التدريب بالنسبة للهدف الحقيقي أو اسم الفئة.model.zero_grad()يقوم بتنظيف حسابات التدرج، بحيث لا يتم تجميعها للمرور التالي.J.backward()يقوم بالانتشار الخلفي والتراكم: فهو يحسب $\nabla_\texttt{x} J$ لكل متغير $\texttt{x}$ والذي حددناه بـrequires_grad=True. يتم تجميع السابق في تدرج كل متغير: $\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$.optimiser.step()يأخذ خطوة في انحدار التدرج: $\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$.
عند تدريب NN ، من المحتمل جدًا أنك بحاجة إلى هذه الخطوات الخمس بالترتيب الذي قُدمت به.
Haya Alsharif
4 Feb 2020