حساب التدرجات لوحدات NN والحيل العملية للانتشار الخلفي
🎙️ Yann LeCunمثال ملموس على الانتشار الخلفي ومقدمة إلى وحدات الشبكة العصبية الأساسية
مثال
في ما يلي، سننظر إلى مثال ملموس على الانتشار الخلفي بمساعدة بعض الرسومات البيانية. الوظيفة العشوائية $G(w)$ هي مدخل لدالة التكلفة $C$ ،والتي يمكن تمثيلها كرسم بياني (a graph). من خلال التلاعب بضرب المصفوفات الجاكوبية، يمكننا تحويل هذا الرسم البياني إلى الرسم البياني الذي سيحسب التدرجات في الاتجاه المعاكس. (لاحظ أن PyTorch و TensorFlow يقومان بذلك تلقائيًا للمستخدم، أي أن الرسم البياني الأمامي “معكوس” تلقائيًا لإنشاء الرسم البياني المشتق والذي يقوم بعملية الانتشار الخلفي للتدرج.)
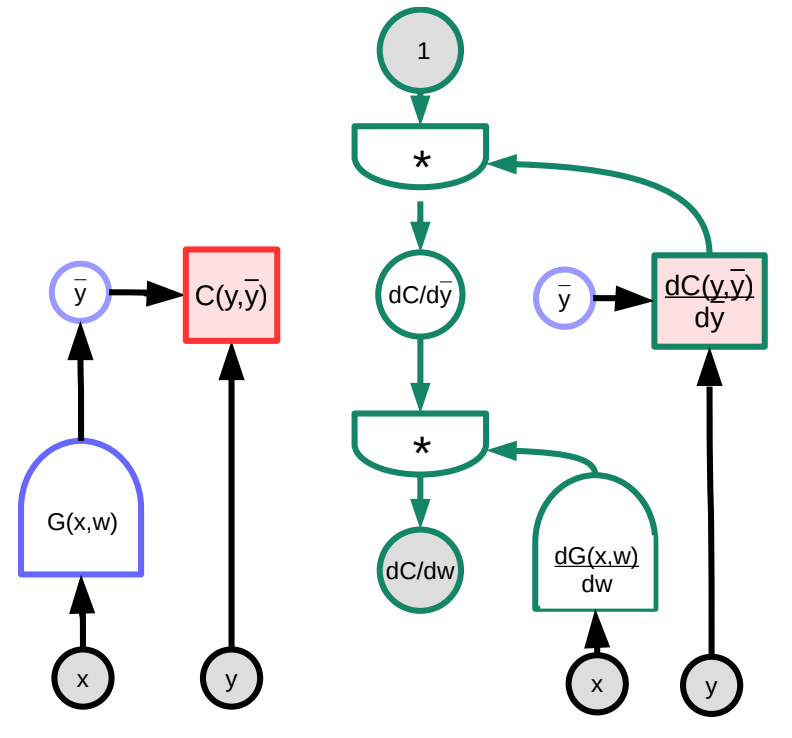
في هذا المثال، يمثل الرسم البياني الأخضر على اليمين مخطط التدرج. بتتبع الرسم البياني ابتداءً من أعلى عقدة، يتبع ذلك
\[\frac{\partial C(y,\bar{y})}{\partial w}=1 \cdot \frac{\partial C(y,\bar{y})}{\partial\bar{y}}\cdot\frac{\partial G(x,w)}{\partial w}\]من حيث الأبعاد، $\frac{\partial C(y,\bar{y})}{\partial w}$ هو متجه صفي بحجم $1\times N$ حيث $N$ هو عدد عناصر $w$; $\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ هو متجه صفي بحجم $1\times M$, حيث $M$ هو عدد حجم المخرجات؛ $\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ هي مصفوفة بحجم $M\times N$, حيث $M$ هو عدد مخرجات $G$ و$N$ هو حجم $w$.
لاحظ أن بعض التعقيدات قد تنشأ عندما لا تكون بنية الرسم البياني ثابتة، ولكنها تعتمد على البيانات. على سبيل المثال، يمكننا اختيار وحدة الشبكة العصبية اعتمادًا على طول متجه الإدخال. على الرغم من أن هذا ممكن، إلا أنه يصبح من الصعب بشكل متزايد إدارة هذا الاختلاف عندما يتجاوز عدد الحلقات رقمًا معقولاً.
وحدات الشبكة العصبية الأساسية
توجد أنواع مختلفة من الوحدات المبنية مسبقًا إلى جانب الوحدات النمطية Linear و ReLU المألوفة. تلك الوحدات مفيدة لأنها مطورة ومحسّنة بشكل فريد لأداء وظائفها الخاصة (على عكس كونها مبنية من خلال مجموعة من الوحدات الأولية الأخرى).
-
خطي: $Y=W\cdot X$
\[\begin{aligned} \frac{dC}{dX} &= W^\top \cdot \frac{dC}{dY} \\ \frac{dC}{dW} &= \frac{dC}{dY} \cdot X^\top \end{aligned}\] -
ReLU: $y=(x)^+$
\[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{otherwise} \end{cases}\]
-
كرر: $Y_1=X$, $Y_2=X$
-
أقرب إلى “Y - splitter” حيث كلا المخرجات والمدخلات متساوية.
-
عند الانتشار الخلفي، يتم تلخيص التدرجات
-
يمكن تقسيمها إلى $ n $ من الفروق
\[\frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}\]
-
-
اجمع: $Y=X_1+X_2$
-
مع جمع متغيرين، عندما يحدث اضطراب في أحدهما، سيضطرب الناتج بنفس الكمية، أي
\[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{and}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]
-
-
كبر: $Y=\max(X_1,X_2)$
- لأنه يمكن أيضًا تمثيل هذه الدالة كما يلي،
-
إذًا، باستخدام قاعدة السلسلة،
\[\frac{dC}{dX_1}=\begin{cases} \frac{dC}{dY}\cdot1 & X_1 > X_2 \\ 0 & \text{else} \end{cases}\]
LogSoftMax مقابل SoftMax
SoftMax ، وهي أيضًا وحدة PyTorch ، هي طريقة ملائمة لتحويل مجموعة من الأرقام إلى مجموعة من الأرقام الموجبة تتراوح ما بين $0$ و $1$ وحاصل جمعها يساوي واحد. يمكن تفسير هذه الأرقام على أنها توزيع احتمالي (probability distribution). لذلك، يتم استخدامه بشكل شائع في مشاكل التصنيف. $y_i$ في المعادلة أدناه هو متجه للاحتمالات لجميع الفئات.
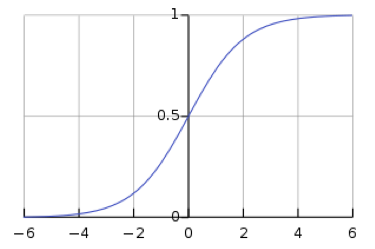
\[y_i = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]ومع ذلك، فإن استخدام softmax يترك الشبكة عرضة لتلاشي التدرجات. يعد التدرج المتلاشي مشكلة، لأنه يمنع تعديل الأوزان في اتجاه التيار بواسطة الشبكة العصبية، مما قد يوقف الشبكة العصبية تمامًا عن التعلم. تُظهر الدالة السيني اللوجيستية (logistic sigmoid function)، وهي دالة softmax لقيمة واحدة، أنه عندما يكون $s$ كبيرًا ، فإن $h(s)$ تساوي $1$، ولما تكون $s$ صغيرة، تساوي $h(s)$ قيمة الـ $0$. نظرًا لأن الدالة sigmoid ثابتة عند $h(s) = 0$ و$h(s) = 1$، فإن التدرج هو $0$، مما ينتج عنه تدرج متلاشي.
توصل علماء الرياضيات إلى فكرة logsoftmax من أجل حل مشكلة التدرج المتلاشي الذي ينشأ من دالة الـ softmax. LogSoftMax هي وحدة نمطية أساسية أخرى في PyTorch. كما يتضح من المعادلة أدناه، LogSoftMax هي مزيج من softmax و log.
\[\log(y_i )= \log\left(\frac{\exp(x_i)}{\Sigma_j \exp(x_j)}\right) = x_i - \log(\Sigma_j \exp(x_j))\]توضح المعادلة أدناه طريقة أخرى للنظر إلى نفس المعادلة. يوضح الشكل أدناه الجزء التالي من الدالة: $\log(1 + \exp(s))$. عندما يكون $s$ صغيرًا جدًا، تكون القيمة $0$، وعندما يكون $s$ كبيرًا جدًا، تصبح القيمة هي $s$. ونتيجة لذلك، لا تتشبع النتيجة وتصل لقيمة قصوى ثابتة (saturate)، وبذلك نتجنب مشكلة التدرج المتلاشي.
\[\log\left(\frac{\exp(s)}{\exp(s) + 1}\right)= s - \log(1 + \exp(s))\]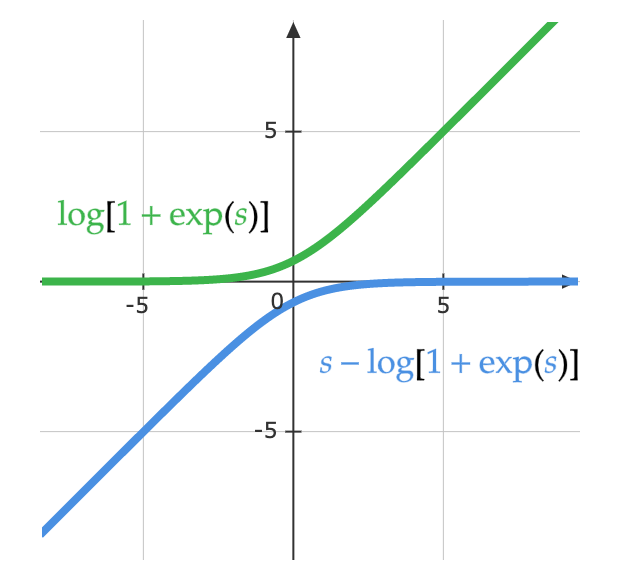
حيل عملية للانتشار الخلفي
استخدم ReLU كدالة التنشيط اللاخطية
يعمل ReLU بشكل أفضل مع الشبكات ذات الطبقات المتعددة، وهذا سبب قلة استخدام بدائل كدالة sigmoid ودوال الظل الزائدية $\tanh(\cdot)$. السبب وراء نجاح هذه الطريقة هو وجود ذاك الالتواء في الدالة والذي يجعلها متكافئة للمقايس المختلفة.
استخدم الخسارة عبر الانتروبيا كدالة الهدف للتصنيف
Log softmax، والذي ناقشناه سابقًا في المحاضرة، هو حالة خاصة من فقدان الانتروبيا. في PyTorch، تأكد من توفير دالة الخسارة عبر الانتروبيا مع log softmax كمدخل (على عكس الـ softmax العادي).
استخدم الانحدار التدرجي العشوائي على حزم صغيرة أثناء التدريب
كما تمت مناقشته سابقًا، تتيح لك الحزم الصغيرة (minibatches) التدريب بشكل أكثر كفاءة نظرًا لوجود تكرار في البيانات؛ لا يجب أن تقوم بالتنبؤ وحساب الخسارة على كل ملاحظة في كل خطوة لتقدير التدرج.
تبديل ترتيب أمثلة التدريب عشوائيًا عند استخدام الانحدار التدرجي العشوائي
الترتيب مهم. إذا رأى النموذج أمثلة فقط من فصيلة واحدة فقط أثناء كل خطوة تدريب، فسوف يتعلم التنبؤ بهذه الفصيلة دون معرفة سبب وجوب توقع تلك الفصيلة. على سبيل المثال، إذا كنت تحاول تصنيف الأرقام من مجموعة بيانات MNIST ولم يتم خلط البيانات، فإن معاملات التحيز في الطبقة الأخيرة ستتنبأ دائمًا بالصفر، ثم تتكيف لتتنبأ دائمًا بواحد، ثم اثنين، إلخ. من الناحية المثالية، يجب أن يكون لديك عينات من كل فصيلة في كل حزمة صغيرة.
ومع ذلك، هناك جدل مستمر حول ما إذا كنت بحاجة إلى تغيير ترتيب العينات في كل دفعة (epoch).
تسوية المدخلات بحيث يكون لها صفرية المتوسط وتباين الوحدة
قبل التدريب، من المفيد تسوية كل خاصية إدخال بحيث يكون لها متوسط صفر وانحراف معياري يساوي الواحد. عند استخدام بيانات صورة RGB، من الشائع أخذ الانحراف المعياري والمتوسط لكل قناة على حدة وتسوية (normalize) الصورة من حيث القناة. على سبيل المثال، خذ المتوسط $m_b$ والانحراف المعياري $\sigma_b$ لجميع القيم الزرقاء في مجموعة البيانات، ثم قم بتسوية القيم الزرقاء لكل صورة على حدة كما يلي
\[b_{[i,j]}^{'} = \frac{b_{[i,j]} - m_b}{\max(\sigma_b, \epsilon)}\]حيث $\epsilon$ رقم صغير عشوائيًا نستخدمه لتجنب القسمة على الصفر. كرر الأمر نفسه للقنوات الخضراء والحمراء. يعد ذلك ضروريًا للحصول على إشارة ذات مغزى من الصور الملتقطة في إضاءة مختلفة؛ على سبيل المثال، تحتوي الصور المضاءة بالنهار على الكثير من اللون الأحمر بينما الصور تحت الماء لا تحتوي على أي شيء تقريبًا.
استخدم جدولًا لخفض معدل التعلم
يجب أن ينخفض معدل التعلم مع استمرار التدريب. عمليًا، يتم تدريب معظم النماذج المتقدمة باستخدام خوارزميات مثل Adam والتي تكيف معدل التعلم بدلاً من SGD البسيط بمعدل تعلم ثابت.
استخدم تنظيم L1 و/أو L2 لتناقص الوزن
يمكنك إضافة تكلفة للأوزان الكبيرة إلى دالة التكلفة. على سبيل المثال، باستخدام تنظيم L2، سنقوم بتعريف الخسارة $w$ وتحديث الأوزان $w$ على النحو التالي:
\[L(S, w) = C(S, w) + \alpha \Vert w \Vert^2\\ \frac{\partial R}{\partial w_i} = 2w_i\\ w_i = w_i - \eta\frac{\partial L}{\partial w_i} = w_i - \eta \left( \frac{\partial C}{\partial w_i} + 2 \alpha w_i \right)\]لفهم سبب تسمية هذا بتناقص الوزن، لاحظ أنه يمكننا إعادة كتابة الصيغة أعلاه لتوضيح أننا نضرب $w_i$ في ثابت أقل من واحد أثناء التحديث.
\[w_i = (1 - 2 \eta \alpha) w_i - \eta\frac{\partial C}{\partial w_i}\]تنظيم L1 (Lasso) مشابه لما سبق، باستثناء أننا نستخدم $\sum_i \vert w_i\vert$ بدلاً من $\Vert w \Vert^2$.
بشكل أساسي، يحاول التنظيم إخبار النظام بتقليل دالة التكلفة إلى الحد الأدنى باستخدام أصغر متجه أوزان ممكن. مع تنظيم L1، يتم تقليص الأوزان غير المفيدة إلى $0$.
تهيئة الوزن
يجب تهيئة الأوزان بشكل عشوائي، ومع ذلك، لا ينبغي أن تكون كبيرة جدًا أو صغيرة جدًا بحيث يكون المخرجات تقريبًا بذات تباين المدخلات. هناك حيل مختلفة لتهيئة الوزن مضمنة في PyTorch. إحدى الحيل التي تعمل جيدًا للنماذج العميقة هي تهيئة Kaiming حيث يتناسب تباين الأوزان عكسياً مع الجذر التربيعي لعدد المدخلات.
استخدام الإسقاط
الإسقاط هو شكل آخر من أشكال التنظيم. يمكن اعتبارها طبقة أخرى من الشبكة العصبية: فهي تأخذ المدخلات، وتضبط عشوائياً $n/2$ من المدخلات للصفر، وتعيد النتيجة كمخرجات. هذا يفرض على النظام أخذ المعلومات من جميع وحدات الإدخال بدلاً من الاعتماد بشكل مفرط على عدد صغير من وحدات الإدخال وبالتالي توزيع المعلومات عبر جميع الوحدات في الطبقة. تم اقتراح هذه الطريقة لأول مرة بواسطة Hinton وآخرون (2012).
لمزيد من الحيل، راجع LeCun وآخرون 1998 .
أخيرًا ، لاحظ أن الانتشار الخلفي لا يعمل فقط مع النماذج المكدسة؛ يمكن أن يعمل مع أي رسم بياني لا دوري موجه أو ما يعرف بـ directed acyclic graph (DAG) طالما أن هناك ترتيب جزئي على الوحدات.
📝 Micaela Flores, Sheetal Laad, Brina Seidel, Aishwarya Rajan
Haya Alsharif
3 Feb 2020