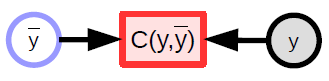مقدمة في خوارزمية الانحدار التدريجي والانتشار الخلفي

🎙️ Yann LeCun

خوازمية تحسين الانحدار التدريجي

النماذج ذات المعاملات

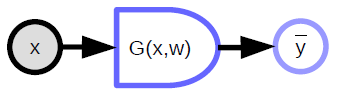
\[\bar{y} = G(x,w)\]

النماذج ذات المعاملات هي ببساطة دوال تعتمد على المدخلات والمعاملات القابلة للتدريب. لا يوجد فرق أساسي بين الاثنين، باستثناء أن المعاملات القابلة للتدريب يتم مشاركتها عبر عينات التدريب حيث تختلف المدخلات من عينة إلى أخرى. في معظم أنظمة التعلم العميق، تكون تلك المعاملات ضمنية، أي لا يتم تمريرها عند استدعاء الدالة. على الأقل في النماذج الموجهة بالكائنات (object-oriented models)، يتم “حفظها تلك المعاملات داخل الدالة” إذا جاز التعبير.

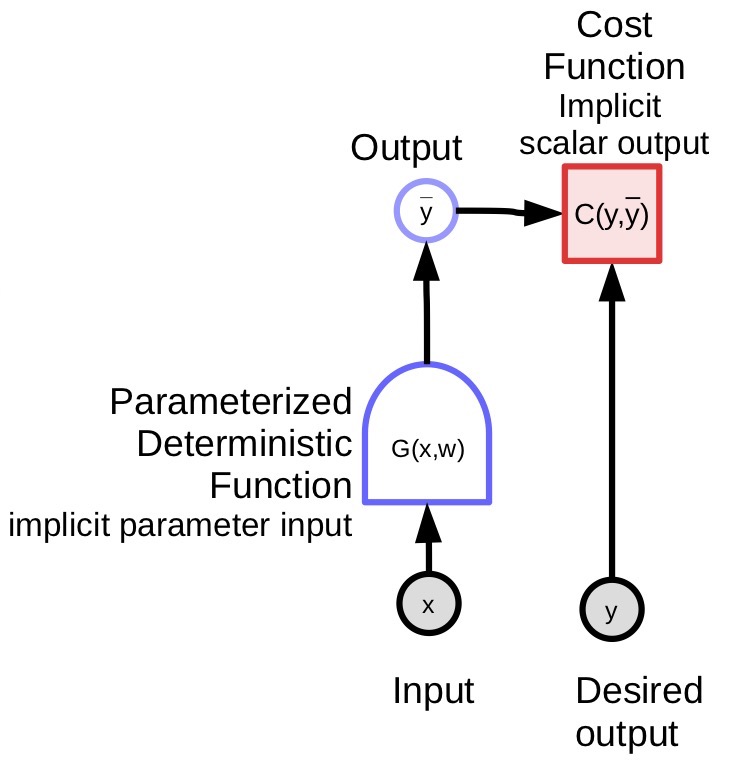
يأخد النموذج ذو المعاملات المدخلات، ويملك متجه من المعاملات، ومن ثم يتنج المخرجات. تدخل تلك المخرجات في حالة التعلم بالإشراف إلى (دالة) وهو دالة التكلفة ($C(y,\bar{y}$))، حيث يتم مقارنة القيمة الفعلية المرادة (${y}$) بمخرجات النموذج ($\bar{y}$). شكل ١ يظهر الرسم البياني الحسابي.

Figure 1: الرسم البياني الحسابي لنموذج بمعاملات

أمثلة على دوال بمعاملات -

• النماذج الخطية - المجموع الموزون لعناصر المتجه المدخل:

\[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• خوارزمية أقرب جار - لدينا مدخل $\vect{x}$ و مصفوفة أوزان $\matr{W}$ يعبر عن كل صف فيها بالرمز $k$. تمثل المخرجات قيمة الصف $k$ من $\matr{W}$ الأقرب إلى $\vect{x}$.

\[\bar{y} = \underset{k}{\arg\min} \Vert x - w_{k,.} \Vert^2\]

قد تشمل النماذج ذات معاملات دوالًا معقدة.

Block diagram notations for computation graphs

• المتغيرات (موتر، عددي، متصل، منفصل)
• مدخلات للنظام يمكن ملاحظتها
• متغير محسوب يتم إنتاجه بواسطة دالة محددة

• الدوالة المحددة

  

• تأخذ مدخلات متعددة ويمكن أن ينتج مخرجات متعددة أيضًا
• تحتوي على متغير معامل ضمني (${w}$)
• يشير الجانب المستدير إلى الاتجاه الذي يسهل فيه الحساب. في الرسم البياني أعلاه، من الأسهل حساب${\bar{y}}$ باستخدام ${x}$ مقارنة بالعكس

• الدوال العددية

  

• تستخدم لتمثيل دالة التكلفة
  • لها ناتج عددي ضمني
  • تأخذ مدخلات عدة وتنتج مخرجًا واحدًا (عادة المسافة بين المدخلات)

دالة الخسارة

دالة الخسارة هي الدالة التي نعمل على التقليل من قيمتها خلال مرحلة التدريب. يوجد نوعان من هذه الخسارة:

1) الخسارة لكل عنصر -

\[L(x,y,w) = C(y, G(x,w))\]

2) متوسط الخسارة -

لكل مجموعة من العينات

\[S = \lbrace(x[p],y[p]) \mid p \in \lbrace 0, \cdots, P-1 \rbrace \rbrace\]

يُمثل متوسط الخسارة على المجموعة $S$ بالآتي:

\[L(S,w) = \frac{1}{P} \sum_{(x,y)} L(x,y,w)\]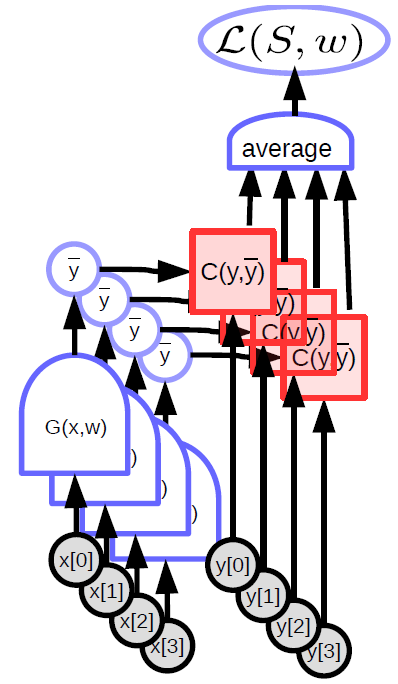

شكل ٢: الرسم البياني الحسابي للنموذج بمتوسط الخسارة

في نموذج التعلم بالإشراف القياسي، فإن الخسارة (لكل عينة) هي ببساطة ناتج دالة التكلفة. يتعلق التعلم الآلي في الغالب بتحسين الدوال (وعادةً ما يكون التحسين بتقليل قيمة نتائجها). يمكن أن يتضمن ذلك أيضًا العثور على توازن ناش (Nash Equilibria) بين وظيفتين كما هو الحال مع شبكات GAN. يتم ذلك باستخدام طرق قائمة على التدرج، ولكن ليس بالضرورة الانحدار التدريجي.

الانحدار التدريجي

الطرق القائمة على التدرج هي طرق/خوارزميات للبحث عن الحد الأدنى لدالة ما، بافتراض أنه يمكن للمرء بسهولة حساب التدرج لتلك الدالة. تفترض تلك الطرق بأن الدالة متصلة وقابلة للتفاضل في كل مكان تقريبًا (ولا يلزم ذلك أن تكون قابلة للتفاضل في كل مكان).

مبدأ الانحدار التدريجي - تخيل أنك في جبل في منتصف ليلة ضبابية. نظرًا لأنك تريد النزول إلى القرية ولديك رؤية محدودة فقط، فبإمكانك فقط النظر حول المنطقة المجاورة لك مباشرة والبحث على اتجاه المنحدر الأكثر حدة، ومن ثم اتخاذ خطوة في ذاك الاتجاه.

طرق مختلفة للانحدار التدريجي

• قاعدة لتحديث الانحدار التدريجي بحزمة كاملة:

\[w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\]

• بالنسبة لـ SGD (الانحدار التدرجي العشوائي)، تصبح قاعدة التحديث كالآتي:

• اختر قيمة لـ $p \in \lbrace 0, \cdots, P-1 \rbrace$، ومن ثم قُم بالتحديث:

\[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

حيث تمثل ${w}$ المعامل الذي نرغب بتحسينه.

$\eta$ هي ثابت عددي في هذه الحالة، ولكن بعض الخوارزميات المتقدمة، تكون عبارة عن مصفوفة.

إذا كانت مصفوفة موجبة شبه مُعرَّفة، فسنظل نتحرك إلى أسفل ولكن ليس بالضرورة في اتجاه أقصى هبوط. في الواقع، قد لا يكون اتجاه الهبوط الحاد دائمًا هو الاتجاه الذي نريد أن نتحرك فيه.

إذا كانت الوظيفة غير قابلة للتفاضل، أي أنها تحتوي على فتحة أو تدرج درجي أو مسطحة، حيث لا يمنحك للتدرج أي معلومات، يجب على المرء أن يلجأ إلى طرق أخرى - تسمى طرقية الترتيب الصفرية أو طرق خالية من التدرج. التعلم العميق قائم على التدرج.

في المقابل، يتضمن التعلم المعزز (RL) تقدير التدرج بدون الشكل الواضح للتدرج. مثال على ذلك هو الروبوت الذي يتعلم ركوب الدراجة حيث يسقط الروبوت بين الحين والآخر. تقيس دالة الهدف مدة بقاء الدراجة دون أن تسقط. لسوء الحظ، لا يوجد تدرج لوظيفة الهدف. يحتاج الروبوت إلى تجربة أشياء مختلفة.

لا يمكن اشتقاق دالة تكلفة الـ RL في معظم الأوقات، لكن الشبكة التي تحسب الناتج تعتمد على التدرج. هذا هو الفرق الرئيسي بين التعلم بالإشراف والتعلم المعزز، حيث تكون دالة التكلفة $C$ في التعلم المعزز غير قابلة للتفاضل. في الواقع هذه الدالة غير معروفة تمامًا، وكل ما تقوم به هو إرجاع مخرجات بناءً على المدخلات إليه، وتعمل مثل الصندوق الأسود. هذا تحديدًا ما يجعلها غير فعالة للغاية وهو أحد المشاكل الرئيسية في الـ RL - خاصة عندما يكون المتجه ذو أبعاد عالية (مما يعني وجود مساحة حل ضخمة للبحث فيها، مما يزيد من صعوبة إيجاد مكان التحرك).

تقنية شائعة جدًا في الـ RL هي طرق انتقاد الفاعل. تتكون طريقة الناقد بشكل أساسي من وحدة C ثانية وهي وحدة معروفة وقابلة للتدريب. يستطيع المرء تدريب الوحدة C والتي يمكن تفاضلها لتقارب دالة التكلفة/المكافأة. حيث للمكافأة قيمة سلبية مشكلةً عقوبة للفاعل. هذه طريقة لجعل دالة التكلفة قابلة للتفاضل، أو على الأقل تقريبها من خلال دالة أخرى قابلة للتفاضل بحيث يمكن للمرء تطبيق الانتشار الخلفي.

مزايا SGD و الانتشار الخلفي للشبكات العصبية التقليدية

مزايا الانحدار التدرجي العشوائي (SGD)

في الممارسة العملية، نستخدم التدرج العشوائي لحساب التدرج لدالة الهدف بالنسبة للمعاملات. بدلاً من حساب التدرج الكامل لدالة الهدف، وهو متوسط جميع العينات، يأخذ التدرج العشوائي عينة واحدة فقط ويحسب الخسارة، $L$، وتدرج الخسارة في المعاملات، ثم يأخذ خطوة واحدة في اتجاه التدرج السلبي.

\[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

في الصيغة أعلاه، تقترب قيمة $w$ من $w$ مطروحًا منها حجم الخطوة، ومضروبةً في اشتقاق دالة الخسارة لكل عينة بالنسبة لمعاملات تلك العينة ($x[p],y[p]$).

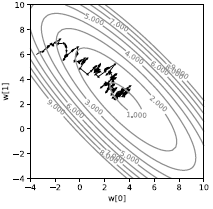
إذا قمنا بذلك على عينة واحدة، فسنحصل على مسار مشوشٍ للغاية كما هو موضح في الشكل 3. بدلاً من الخسارة التي تنحدر مباشرة، فإنها عشوائية (stochastic). وستسحب كل عينة الخسارة نحو اتجاه مختلف. فقط المتوسط هو ​​الذي يقودنا إلى الحد الأدنى من المتوسط. على الرغم من أنها تبدو غير فعالة، إلا أنها على الأقل أسرع بكثير من الانحدار التدريجي بحزمة كاملة في سياق التعلم الآلي عندما تحتوي العينات على بعض من التكرار.

الشكل 3: مسار نزول الانحدار التدرجي العشوائي لتحديث كل عينة

من الناحية العملية، نستخدم الدُفعات بدلاً من إجراء انحدار تدريجي عشوائي على عينة واحدة. من ثم نحسب متوسط التدرج على مجموعة من العينات، وليس عينة واحدة، ثم نأخذ خطوة واحدة. السبب الوحيد للقيام بذلك هو أنه الدفعات تمكنا من الاستفادة بشكل أكثر كفاءة من الأجهزة الموجودة (على سبيل المثال، وحدات GPU و CPU متعددة النواة) لأنه من السهل تنفيذها على التوازي. الدفعات هو أبسط طريقة للتوازي.

الشبكة العصبية التقليدية

الشبكات العصبية التقليدية هي في الأساس طبقات متناثرة من العمليات الخطية والعمليات غير الخطية النقطية. بالنسبة للعمليات الخطية، من الناحية المفاهيمية، فهي مجرد عملية ضرب متجه بمصفوفة. نأخذ المتجه (المدخلات) ونضربه في مصفوفة مكونة من الأوزان. النوع الثاني من العملية هو أخذ كافة مكونات متجه المجاميع الموزونة ونمررها من خلال بعض العمليات اللاخطية البسيطة (على سبييل المثال $\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, …).

الشكل 4: الشبكة العصبية التقليدية

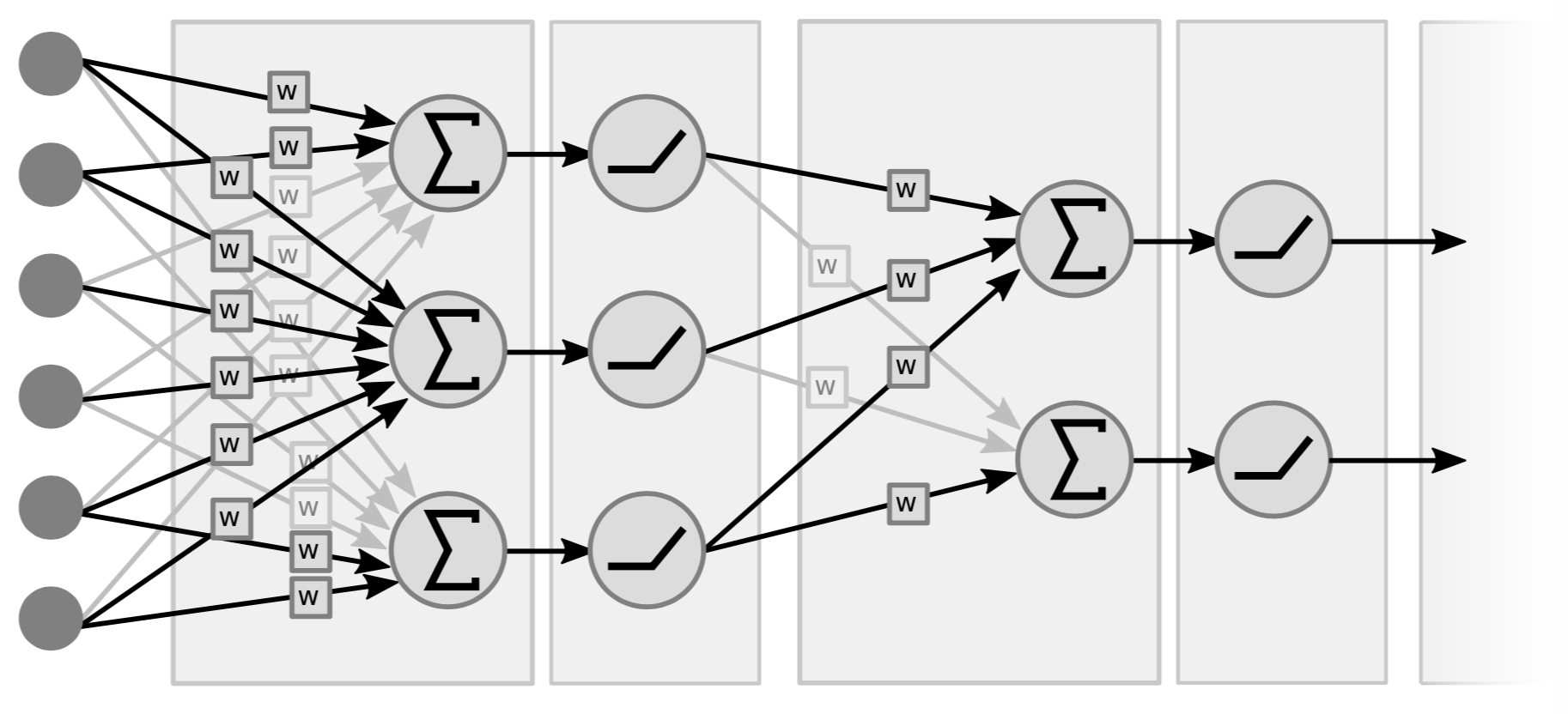الشكل 4 مثال لشبكة من طبقتين، لأن ما يهم هو زوجي الطبقات (الخطية + واللاخطية). يسميها بعض الناس شبكة من 3 طبقات لأنهم يحسبون المتغيرات كطبقة. لاحظ أنه إذا لم تكن هناك عناصر غير خطية في الوسط، فقد يكون لدينا أيضًا طبقة واحدة لأن ضرب دالتين خطيتين هو دالة خطية واحدة.

يوضح الشكل 5 كيفية تتكدس مجموعات الدوال الخطية واللاخطية:

الشكل 5: النظر داخل الكتل الخطية وغير الخطية

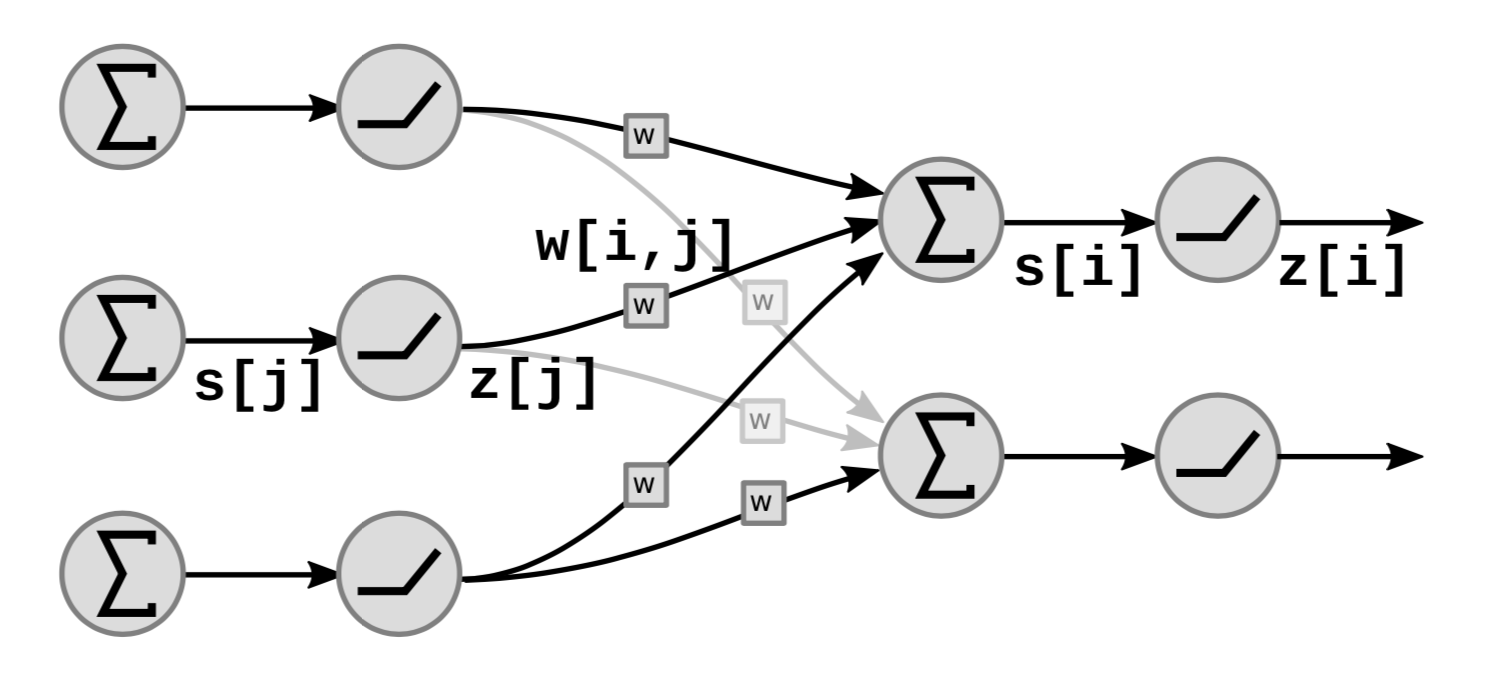في الرسم البياني، $s[i]$ هو المجموع الموزون للوحدة ${i}$ والذي يتم حسابه على النحو التالي:

\[s[i]=\sum_{j \in UP(i)}w[i,j]\cdot z[j]\]

حيث يشير $UP(i)$ إلى أسلاف $i$ و $z[j]$ هو الناتج العنصر رقم $j$ من الطبقة السابقة.

الناتج $z[i]$ يحسب على النحو التالي:

\[z[i]=f(s[i])\]

حيث $f$ دالة غير خطية.

الانتشار الخلفي من خلال دالة غير خطية

الطريقة الأولى للقيام بالانتشار الخلفي هي إعادة الانتشار من خلال دالة غير خطية. نأخذ دالة غير خطية معينة $h$ من الشبكة ونترك كل شيء آخر في الصندوق الأسود.

الشكل 6: الانتشار الخلفي من خلال دالة غير خطية

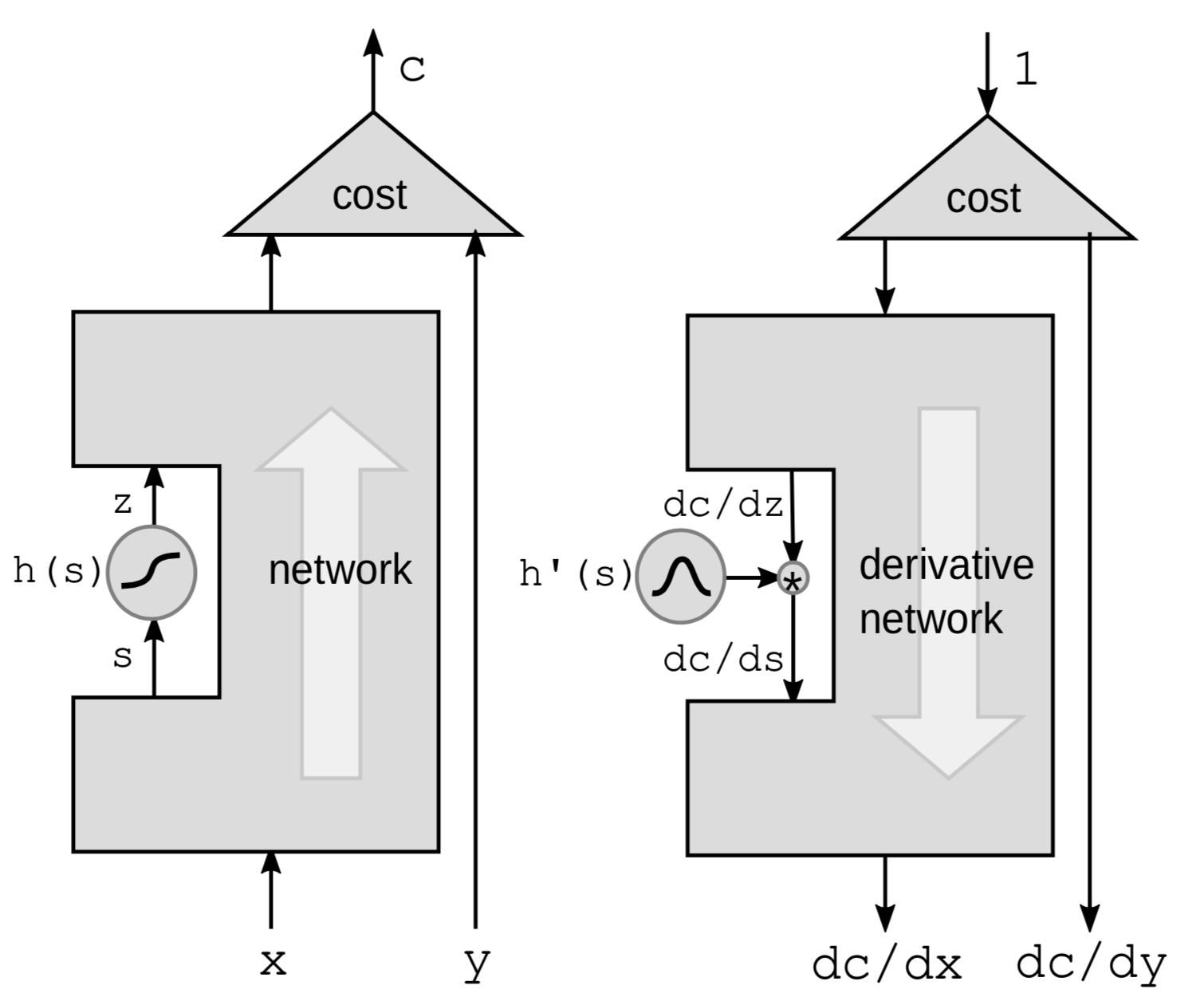سنستخدم قاعدة السلسلة لحساب التدرجات:

\[g(h(s))' = g'(h(s))\cdot h'(s)\]

حيث $h’(s)$ هو مشتق $z$ بالنسبة إلى $s$ ويمثله $\frac{\mathrm{d}z}{\mathrm{d}s}$. لتوضيح العلاقة بين المشتقات، نعيد كتابة الصيغة أعلاه على النحو التالي:

\[\frac{\mathrm{d}C}{\mathrm{d}s} = \frac{\mathrm{d}C}{\mathrm{d}z}\cdot \frac{\mathrm{d}z}{\mathrm{d}s} = \frac{\mathrm{d}C}{\mathrm{d}z}\cdot h'(s)\]

ومن ثم، إذا كان لدينا سلسلة من هذه الدوال في الشبكة، فيمكننا الانتشار للخلف من خلال الضرب في مشتقات جميع الدوال ${h}$ واحدة تلو الأخرى طوال الطريق للخلف.

من البديهي التفكير في الأمر من منظور الاضطرابات. سيؤدي اضطراب $s$ بمقدار $\mathrm{d}s$ إلى إرباك $z$ بواسطة:

\[\mathrm{d}z = \mathrm{d}s \cdot h'(s)\]

سيؤدي هذا بدوره إلى إرباك $C$ من خلال:

\[\mathrm{d}C = \mathrm{d}z\cdot\frac{\mathrm{d}C}{\mathrm{d}z} = \mathrm{d}s\cdot h’(s)\cdot\frac{\mathrm{d}C}{\mathrm{d}z}\]

مرة أخرى، ينتهي بنا الأمر بنفس الصيغة الموضحة أعلاه.

الانتشار الخلفي من خلال المجموع الموزون

بالنسبة لوحدة نمطية خطية، نطبق الانتشار الخلفي باستخدام المجموع المرجح. هنا، ننظر إلى الشبكة بالكامل على أنها صندوق أسود باستثناء 3 توصيلات تنطلق من متغير ${z}$ إلى مجموعة متغيرات $s$.

الشكل 7: الانتشار الخلفي من خلال المجموع الموزون

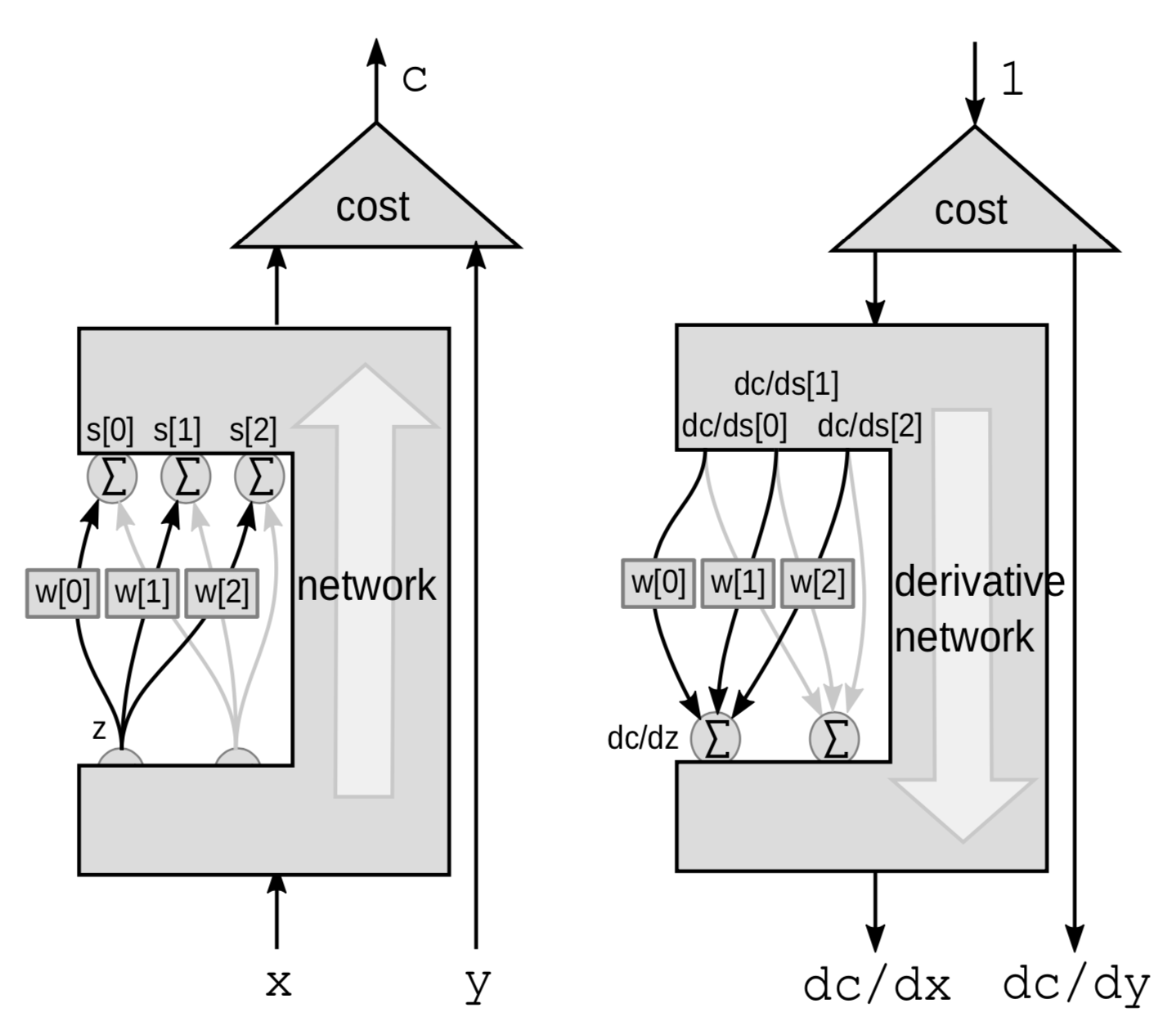هذه المرة، الاضطراب هو المجموع الموزون. يؤثر $Z$ على عدة متغيرات. سيؤدي تشويش $z$ بواسطة $\mathrm{d}z$ إلى إرباك $s[0]$ و $s[1]$ و $s[2]$ بواسطة:

\[\mathrm{d}s[0]=w[0]\cdot \mathrm{d}z\] \[\mathrm{d}s[1]=w[1]\cdot \mathrm{d}z\] \[\mathrm{d}s[2]=w[2]\cdot\mathrm{d}z\]

سيؤدي هذا إلى اضطراب $C$ بواسطة

\[\mathrm{d}C = \mathrm{d}s[0]\cdot \frac{\mathrm{d}C}{\mathrm{d}s[0]}+\mathrm{d}s[1]\cdot \frac{\mathrm{d}C}{\mathrm{d}s[1]}+\mathrm{d}s[2]\cdot\frac{\mathrm{d}C}{\mathrm{d}s[2]}\]

ومن ثم، فإن $C$ ستختلف باختلاف مجموع الأشكال الثلاثة:

\[\frac{\mathrm{d}C}{\mathrm{d}z} = \frac{\mathrm{d}C}{\mathrm{d}s[0]}\cdot w[0]+\frac{\mathrm{d}C}{\mathrm{d}s[1]}\cdot w[1]+\frac{\mathrm{d}C}{\mathrm{d}s[2]}\cdot w[2]\]

[تطبيق باستخدام PyTorch للشبكة العصبية وخوارزمية عامة للانتشار الخلفي] (https://www.youtube.com/watch؟v=d9vdh3b787Y&t=2288s)

رسم تخطيطي للشبكة العصبية التقليدية

• الأجزاء الخطية $s_{k+1}=w_kz_k$
• الأجزاء غير الخطية $z_k=h(s_k)$

$w_k$: مصفوفة $z_k$: متجه $h$: تطبيق دالة عددية ${h}$ لكل مكون. هذه شبكة عصبية من 3 طبقات مع أزواج من الدوال الخطية وغير الخطية، ولكن معظم الشبكات العصبية الحديثة لا تحتوي على مثل هذه الفواصل الخطية وغير الخطية الواضحة وعادة ما تكون أكثر تعقيدًا.

تطبيق باستخدام PyTorch

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # flatten input tensor
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

• يمكننا تطبيق الشبكات العصبية باستخدام فئات كائنية التوجه (object oriented classes) في PyTorch. أولاً، نحدد الـ class للشبكة العصبية ونهيئ الطبقات الخطية في الـ constructor باستخدام فئة nn.Linear المعرفة مسبقًا. يجب أن تكون الطبقات الخطية كائنات منفصلة لأن كل منها تحتوي على متجه من المعاملات. تضيف nn.Linear class أيضًا متجه التحيز (bias vector) ضمنيًا. ثم نقوم بتعريف دالة forward تُعرّف كيفية حساب المخرجات بدالة $\text{torch.relu}$ كتفعيل غير خطي. لا يتعين علينا تهيئة (initialize) وظائف relu منفصلة لأنها لا تحتوي على معاملات.

• لسنا بحاجة إلى حساب التدرج بأنفسنا لأن PyTorch يعرف كيفية دعم الانتشار وحساب التدرجات مع الأخذ في الاعتبار دالة “forward”.

الانتشار الخلفي من خلال وحدة وظيفية

نقدم الآن شكلاً أكثر عمومية من الانتشار الخلفي.

الشكل 8: الانتشار الخلفي من خلال وحدة وظيفية

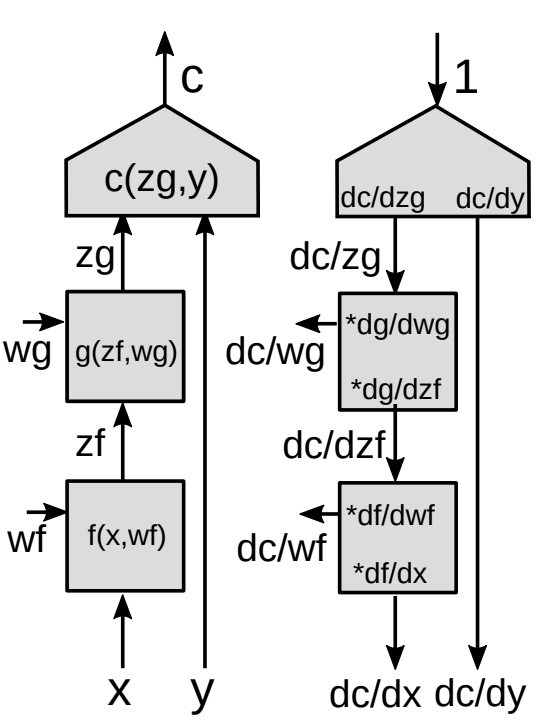• استخدام قاعدة السلسلة لدوال المتجهات

\[z_g : [d_g\times 1]\] \[z_f:[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

هذه هي الصيغة الأساسية لـ $\frac{\partial c}{\partial{z_f}}$ باستخدام قاعدة السلسلة. لاحظ أن التدرج لدالة عددية بالنسبة إلى المتجه هو متجه له نفس حجم المتجه الذي تشتقه. من أجل جعل الرموز متسقة، فإن المتجه عبارة عن بدلاً من عمود.

• مصفوفة جاكوبية

\[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

نحتاج إلى $\frac{\partial {z_g}}{\partial {z_f}}$ دولار (عناصر مصفوفة جاكوبية) لحساب تدرج دالة التكلفة بالنسبة إلى $z_f$ باعتبار أن انحدار دالة التكلفة بالنسبة إلى $z_g$ معطى. كل عنصر $ij$ يساوي الاشتقاق الجزئي للعنصر رقم $i$ من متجه المخرجات بالنسبة للعنصر $j$ من متجه المدخلات.

إذا كان لدينا سلسلة من الوحدات، فإننا نستمر في ضرب المصفوفات الجاكوبية لجميع الوحدات في الأسفل ونحصل على التدرجات مع جميع المتغيرات الداخلية.

الانتشار الخلفي من خلال رسم بياني متعدد المراحل

لنأخد في عين الاعتبار مجموعة من العديد من الوحدات في الشبكة العصبية كما هو موضح في الشكل 9.

الشكل 9: الانتشار الخلفي من خلال رسم بياني متعدد المراحل

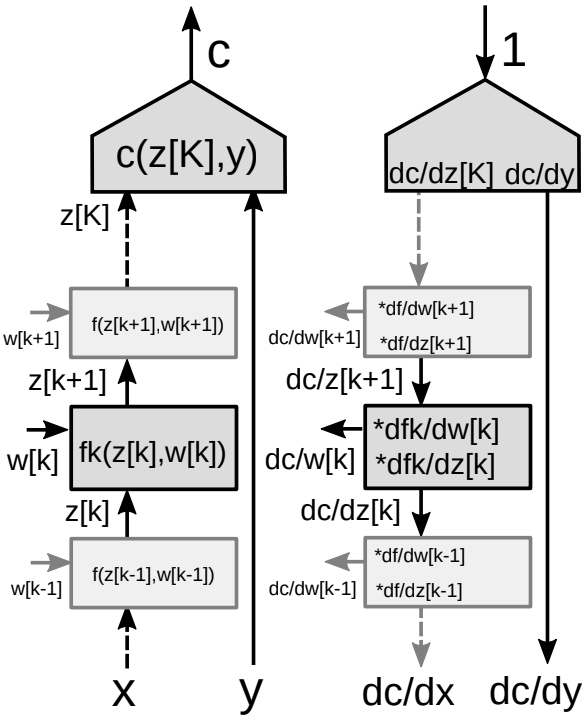بالنسبة لخوارزمية الانتشار الخلفي، نحتاج إلى مجموعتين من التدرجات - واحدة بالنسبة إلى الحالات أو ما يعرف بـ states (كل وحدة من وحدات الشبكة) والأخرى بالنبسة إلى الأوزان (جميع المعاملات في وحدة معينة). لذلك لدينا مصفوفتان جاكوبيتان مرتبطتان بكل وحدة. يمكننا مرة أخرى استخدام قاعدة السلسلة للانتشار الخلفي.

• استخدام قاعدة السلسلة للدوال المتجهة

\[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• مصفوفتان جاكوبيتان للوحدة
  • واحد بالنسبة إلى $z[k]$
  • واحد بالنسبة إلى $w[k]$

---

📝 Amartya Prasad, Dongning Fang, Yuxin Tang, Sahana Upadhya
Haya Alsharif
3 Feb 2020