تحفيز المشكلة والجبر الخطي والتمثيل
🎙️ Alfredo Canzianiالمراجع
يرجى مراجعة حساب ألفريدو كنزياني على تويتر @alfcnz. على سبيل المثال، بإمكانك إيجاد العديد من الفيديوهات والكتب بتفاصيل ذات علاقة بالجبر الخطي وتحليل القيم المنفردة (SVD) عن طريق كتابة linear algebra (from:alfcnz) في خانة البحث.
التحولات والتحفيز
كمثال تحفيزي دعونا ننظر لتصنيف الصور، لنفترض بأننا ألتقطنا صوره من كاميرا وضوحها ١ ميجابيكسل. هذه الصوره سوف تحتوي على مايقارب ١٠٠٠ بيكسل عامودي و١٠٠٠ بيكسل أفقي، وكل بيكسل مكون من ثلاث أبعاد لونيه: أحمر و أخضر وأزرق (RGB). وبالتالي كل صوره تعتبر كنقطه في فضاء ذو 3 ملايين بُعد. وبوجود حجم هائل من الأبعاد قد نريد تصنيف العديد من الصور المثيره للإهتمام -كتصنيف صورة القط مقابل صورة الكلب- ولكنها سوف تكون بنفس المنطقه في هذه الأبعاد.
لتصنيف هذه الصور بطريقه فعّاله علينا الأخذ بعين الإعتبار الطرق المختلفة لتحويل البيانات وتغيير موقع النقاط. علينا أن نتذكر أن في البعد الثنائي (2D) التحويل الخطي هو نفس ضرب المصفوفة. كمثال التحويل الخطي التالي:
-
الدوران (عندما تكون المصفوفة متعامدة).
-
التحجيم (عندما تكون المصفوفة قطرية).
-
الإنعكاس (عندما تكون المحددة سالبة).
-
القص.
مع ملاحظة أن عملية التحريك لوحدها لا تعد خطية لأن الصفر لا يناظر الصفر بعد العملية ولكن هو عباره عن تحويل تآلفي (affine transformation). والآن نعود لمثال الصوره الذي بدأنا به، حيث نقوم بتحويل نقاط البيانات بتحريكها لتصبح حول نقطة الصفر ونحجمها باستخدام المصفوفة القطرية وكأننا قمنا بعمل “تكبير” المنطقة. وأخيرا نستطيع عمل التصنيف عن طريق إيجاد خطوط عبر الفضاء حيث يقوم الخط بفصل النقاط المختلفة وتصنيفها بالشكل المناسب. بعبارة أخرى الفكرة هي إستخدام التحويل الخطي وغير الخطي لنقل تلك النقاط إلى فضاء جديد يسمح لنا بفصلها بواسطة خط مستقيم. هذه الفكره ستكون أكثر وضوحا خلال الأقسام التالية.
تمثيل البيانات – فصل النقاط حسب اللون بإستخدام الشبكة
في النموذج أدناه، لدينا خمس تفرعات لولبية لكل منها لون مختلف. توجد النقاط في فضاء ثنائي البعد ونستطيع تمثيلها بزوجين من الأرقام ويمثل اللون بُعدًا ثالثًا نستخدمه للتصنيف بين النقاط. وبعد ذلك نستطيع إستخدام الشبكة العصبية لفصل كل نقطة من النقاط بناءً على اللون.
 |
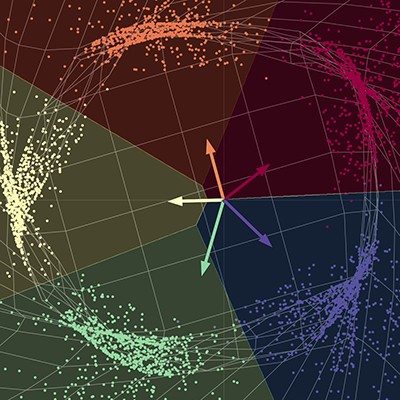 |
| (أ) النقاط المدخلة، ما قبل الشبكة | (ب) النقاط المخرجة، ما بعد الشبكة |
تقوم الشبكة /”بتمديد/” نسيج الفضاء حتى نستطيع فصل كل نقطة إلى أجزاء فرعية مختلفة. عند التقارب للتنيجة نجد أن الشبكة قد فصلت كل لون إلى فضاء فرعي مختلف من المتشعب النهائي (manifold). بعبارة أخرى يمكن فصل كل لون في الفضاء الجديد فصله بشكل خطي عن طريق استخدام انحدار واحد مقابل عدة انحدارات. يمكن تمثيل المتجهات بالرسم التوضيحي عن طريق مصفوفه بحجم 2 $times$ 5، وضرب تلك المصفوفة بكل نقطة لاسترجاع درجة كل لون من الألوان الخمسة. حينئذ يمكن تصنيف النقاط باللون حسب درجات كل نقطة. تتكون المخرجات من خمسة عناصر، حيث يمثل كل منها لونًا ما، بينما تتكون المدخلات من عنصرين واحد للإحداثي السيني وآخر للإحداثي الصادي للنقاط. للتلخيص هذه الشبكة تأخذ نسيج الفضاء وتقوم بتشكيله باستخدام عدة مصفوفات يتلوها عمليات لاخطية.
معمارية الشبكة
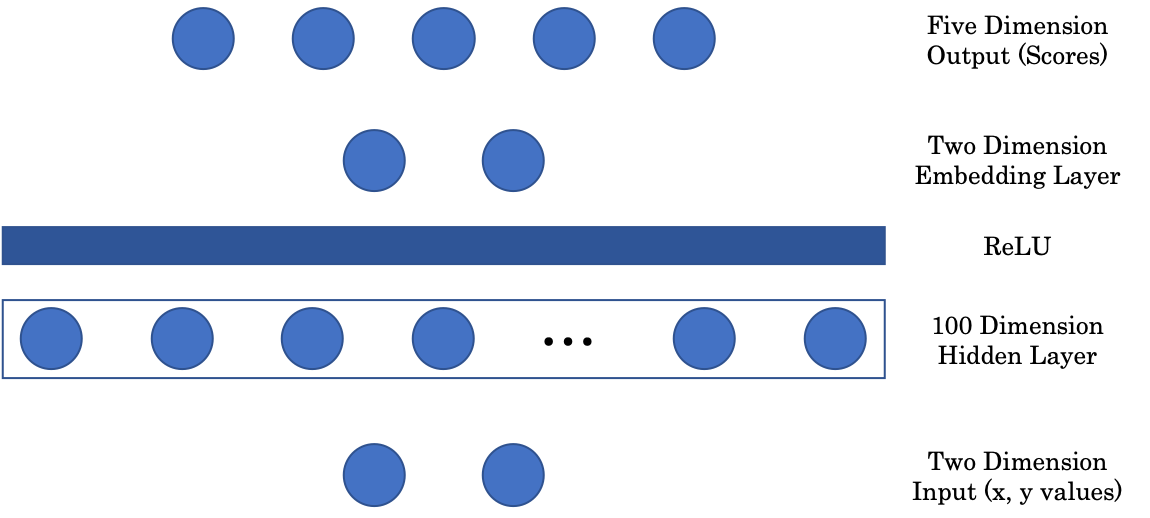
شكل ٢: هندسة الشبكة
تربط المصفوفة الأولى المدخل ثنائي الأبعاد بطبقة خفية وسطية ذات ١٠٠ بعد. لدينا وبعد ذلك طبقة لاخطية ألا وهي دالة ReLU وهي وحدة خطية مصححة، والتي تعبر ببساطة عن الجزء الموجب $(\cdot)^+$ من المعادلة. وليتم عرض الصورة بشكل رسومي نضيف طبقة التضمين (embedding layer) والتي تقوم بربط الطبقة الخفية المدخلة ذات الـ ١٠٠ بُعد بمخرج ثنائي الأبعاد. أخيرا يتم إسقاط طبقة التضمين على الطبقة ذات الأبعاد الخمسة في الشبكة، والتي تمثل قيمة لكل لون.
إسقاطات عشوائية – مفكرة جوبيتر
مفكرة جوبيتر بالإمكان الوصول لها من هنا. للتمكن من تشغيل المفكرة عليك التأكد من تحميل بيئة pDL كما هو موضح في README.md.
جهاز PyTorch
بالإمكان تشغيل PyTorch على كلاً من الـ CPU أو الـ GPU. يعد الـ CPU مناسبًا للمهام المتسلسلة بينما يناسب الـ GPU المهام المتوازية. قبل تنفيذ البرنامج على الجهاز المطلوب علينا التأكد من أن الموترات (tensors) والنماذج قد تم نقلها على ذاكرة الجهاز. بالإمكان عمل ذلك باستخدام هذين السطرين:
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)
يعرف السطر الأول متغير يسمى device ويعنيه للـ GPU في حال توفره، أو للـ CPU كقيمة افتراضية. في السطر الثاني، يتم إنشاء الموتر ويرسل لذاكرة الجهاز عن طريق إستدعاء to(device).
إرشادات مفكرة جوبيتر
للاطلاع على التعليمات الخاصة بدالة ما في أحد خلايا المفكرة اضغط Shift + Tab
تصوير التحولات الخطية
تذكر أنه بالإمكان تمثيل التحويلات الخطية كمصفوفة عن طريق تحليل القيمة المنفردة، بإمكاننا تحليل هذه المصفوفة إلى ثلاث مصفوفات مكونة لها يمثل كلٌ منها تحولاً خطيًا مختلفًا.
\[W = U\begin{bmatrix}s_1 & 0 \\ 0 & s_2 \end{bmatrix} V^\top\]في المعادلة رقم (١) المصفوفتان $U$ و$V^\top$ متعامدتان ويمثلان تحولات الدوران والانعكاس. المصفوفة الوسطى قطرية وتمثل تحول في الحجم.
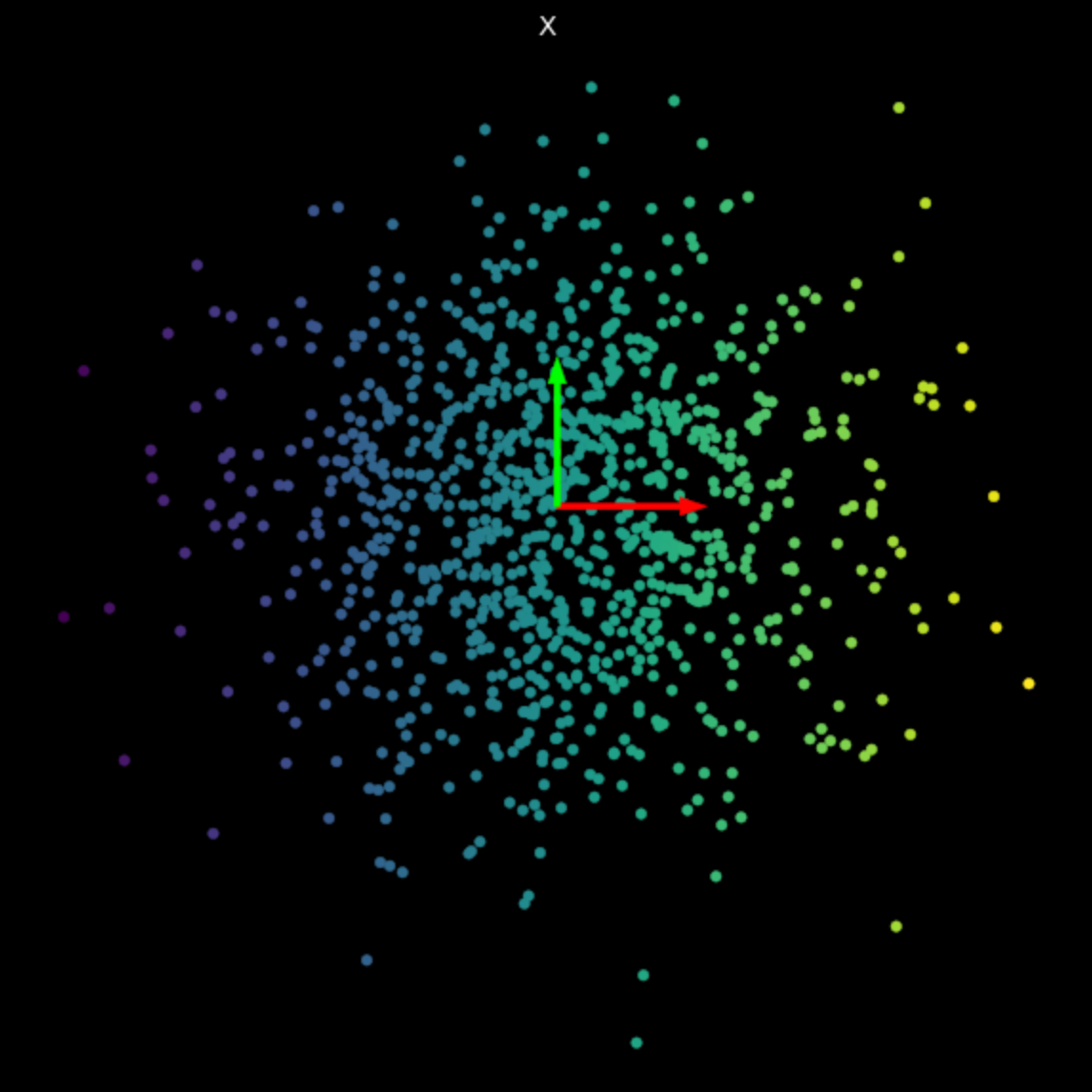
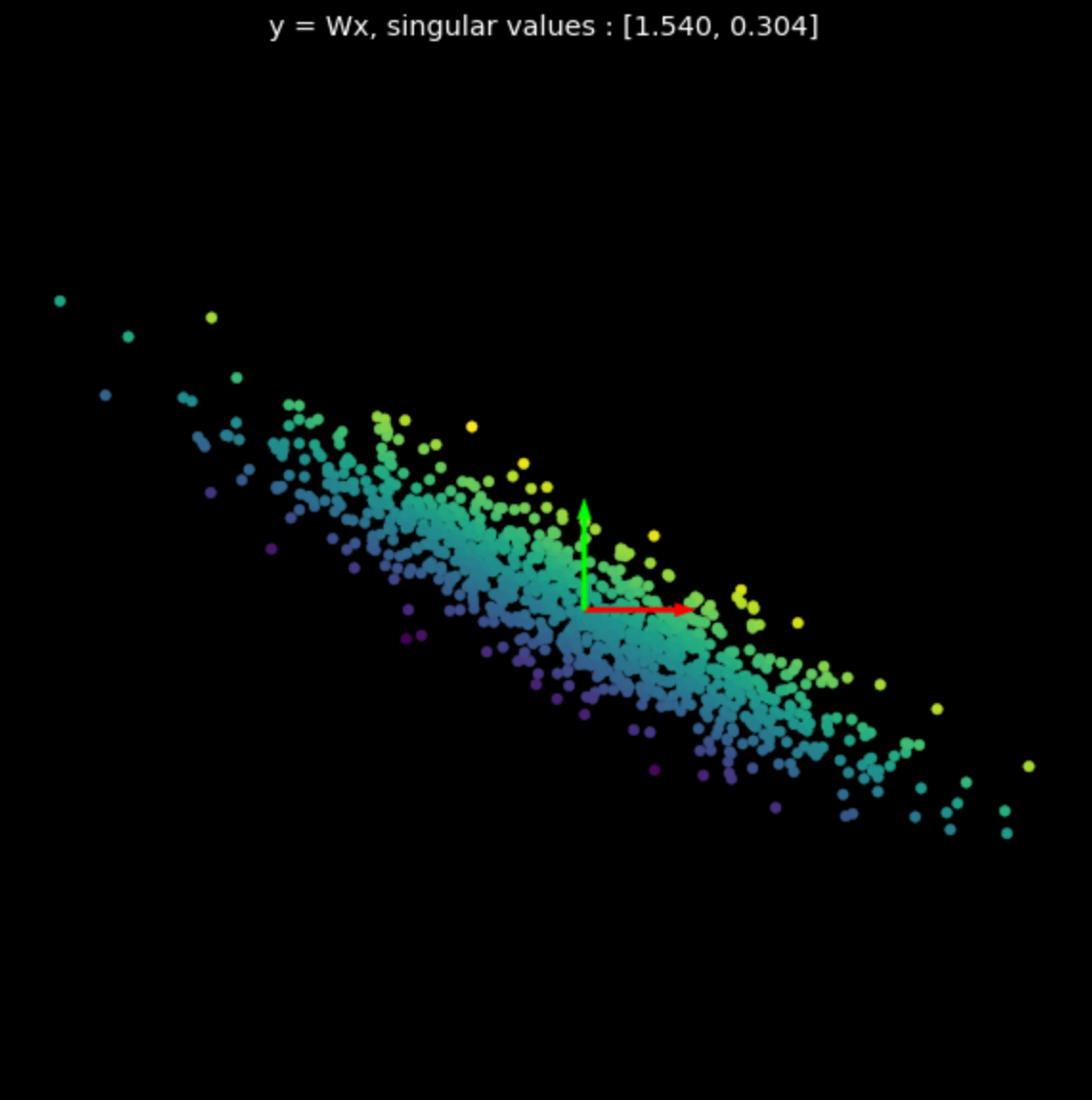
مثلنا التحولات الخطية للعديد من المصفوفات العشوائية في شكل ٣. لاحظ تأثير القيم الفردية على التحولات الناتجة.
تم إنشاء المصفوفات المستخدمة باستخدام Numpy ؛ وبالرغم من ذلك، يمكننا أيضًا استخدام فئة nn.Linear من PyTorch مع بقيمة bias = False لإنشاء تحويلات خطية.
 |
 |
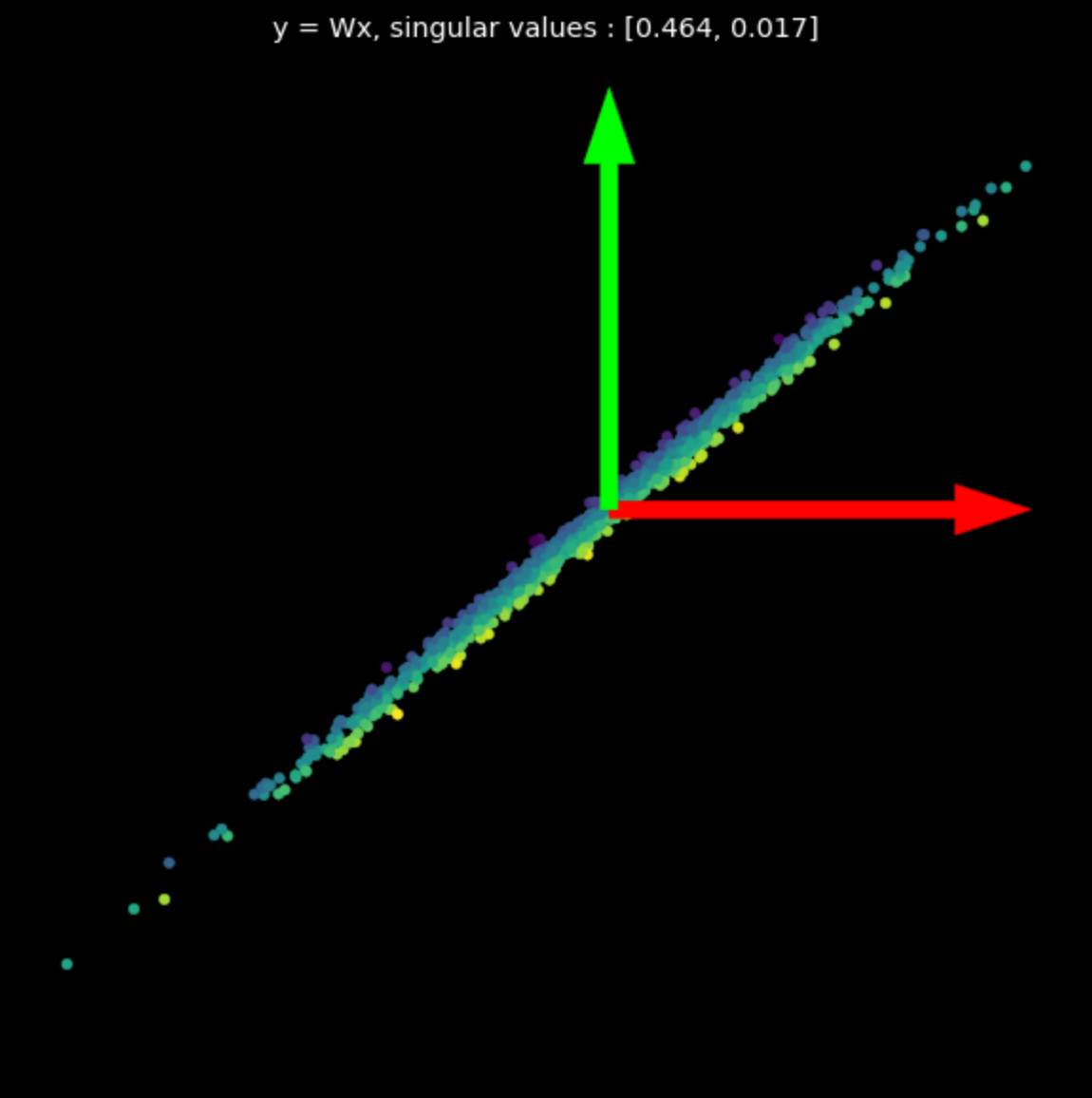 |
| (أ) النقاط الأساسية | (ب) $s_1$ = 1.540, $s_2$ = 0.304 | (ج) $s_1$ = 0.464, $s_2$ = 0.017 |
التحولات غير الخطية
لنقوم الآن بتمثيل التحول التالي
\[f(\vx) = \tanh\bigg(\begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \vx \bigg)\]تذكر رسمة $\tanh(\cdot)$ في شكل ٤
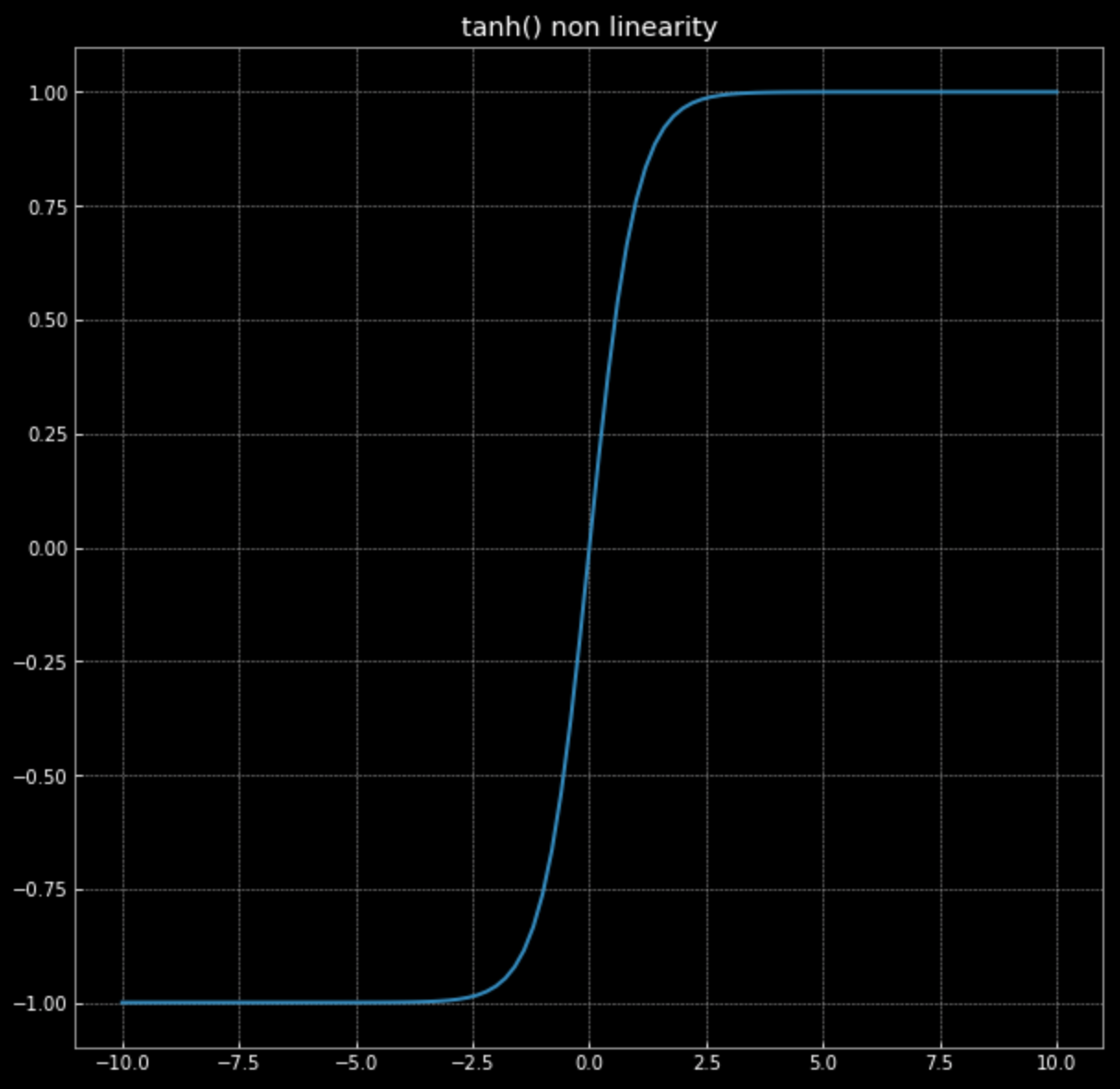
الشكل ٤: الظل الزائدي غير الخطي
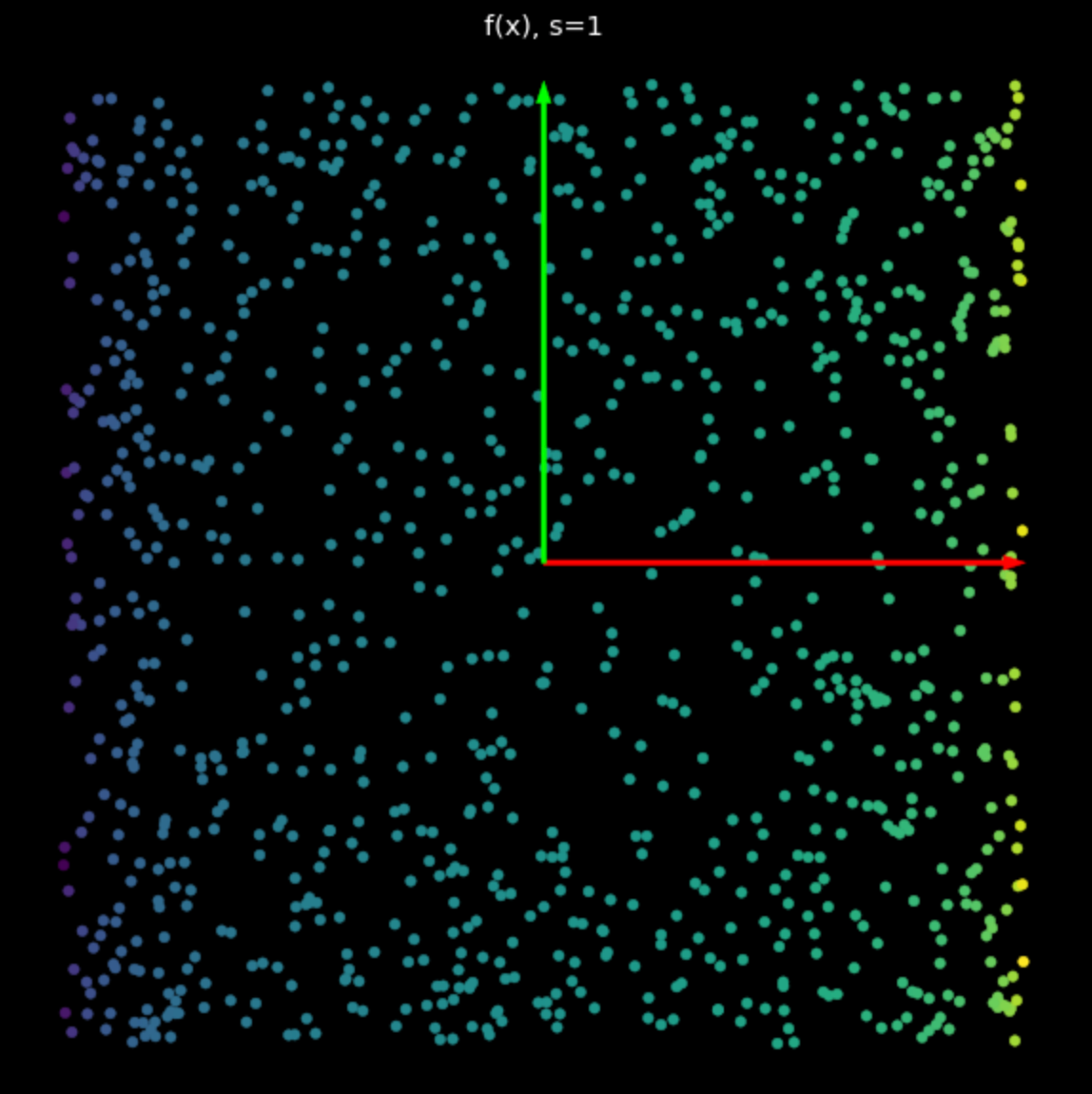
تقوم عدم الخطية بحد القيم ما بين -١ و +١ مشكلةً مربعًا. عندما تزداد قيمة s في المعادلة (٢) فإن ذلك يدفع النقاط أكثر فأكثر لأطراف المربع كما هو موضح في شكل ٥. يمكن ذلك الدفع للأطراف من إبعاد ا لنقاط عن بعضها البعض حتى نتمكن من تصنيفها.
 |
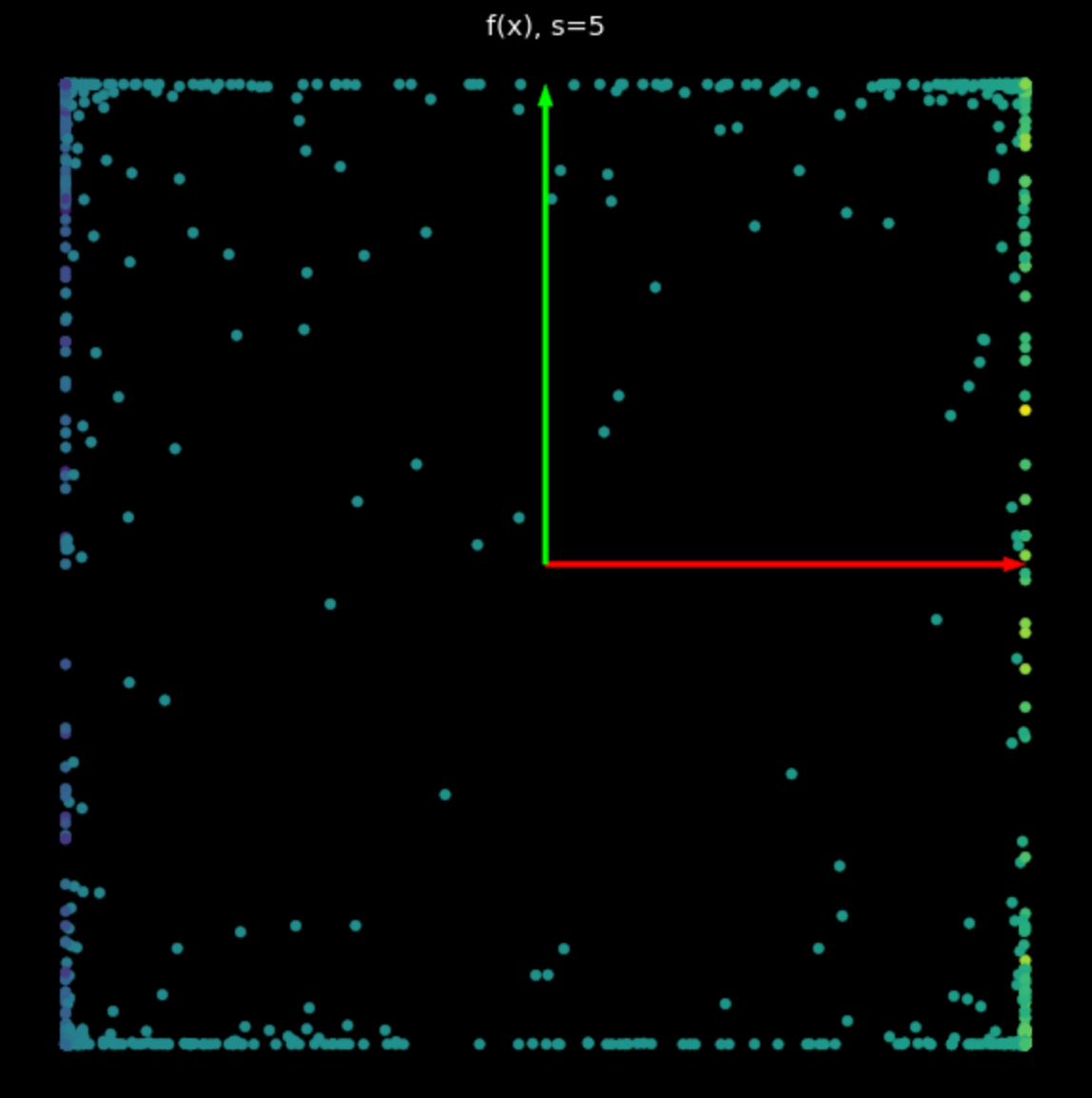 |
| (أ) اللاخطية مع $s=1$ | (ب) اللاخطية مع $s=5$ |
الشبكات العصبية العشوائية
أخيرا وليس آخرا، نقوم بتمثيل التحولات التي حدثت باستخدام شبكه عصبيه بسيطة غير مدربة. الشبكة تتكون من طبقة خطية تقوم بتحليل تآلفي يعقب ذلك مماس زائدي للتعامل مع اللاخطية وأخيرا طبقة خطية أخرى. عند فحص التحول بالشكل ٦ نرى أنه مختلف عن التحولات الخطية وغير الخطية التي رأيناها مسبقا. سوف نرى كيف نجعل هذه التحولات التي تقوم بها الشبكات العصبية مفيدة لهدفنا النهائي ألا وهو التصنيف.
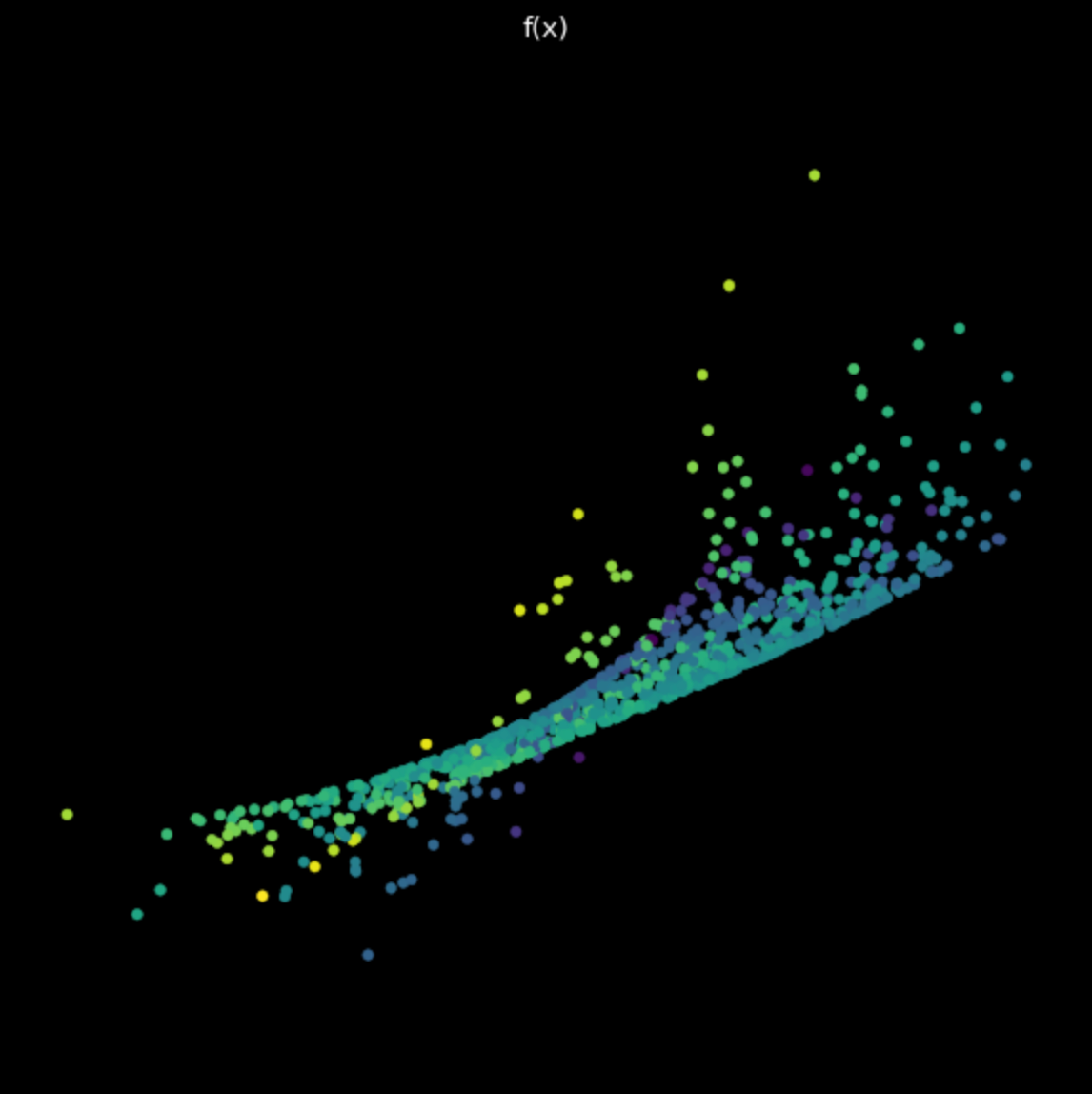
الشكل ٦: التحول من شبكة عصبية غير مدربة
📝 Derek Yen, Tony Xu, Ben Stadnick, Prasanthi Gurumurthy
Reem AlYami
28 Jan 2020